高等数学 8.5 曲面及其方程
文章目录
- 一、曲面研究的基本问题
- 二、旋转曲面
- 三、柱面
- 四、二次曲线
- 1. 椭圆锥面 x2a2+y2b2=z2\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} = z^2a2x2+b2y2=z2
- 2.椭球面 x2a2+y2b2+z2c2=1\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} + \cfrac{z^2}{c^2} = 1a2x2+b2y2+c2z2=1
- 3.单叶双曲面 x2a2+y2b2−z2c2=1\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} - \cfrac{z^2}{c^2} = 1a2x2+b2y2−c2z2=1
- 4.双叶双曲面 x2a2−y2b2−z2c2=1\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} - \cfrac{z^2}{c^2} = 1a2x2−b2y2−c2z2=1
- 5.椭圆抛物面 x2a2+y2b2=z\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} = za2x2+b2y2=z
- 6.双曲抛物面 x2a2−y2b2=z\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} = za2x2−b2y2=z
一、曲面研究的基本问题
在空间解析几何中,关于曲面的研究有下列两个基本问题:
(1)已知一曲面作为点的几何轨迹时,建立这曲面的方程;
(2)已知坐标 x,y,zx, y, zx,y,z 间的一个方程时,研究这方程所表示的曲面的形状。
如球心在点 M0(x0,y0,z0)M_0(x_0, y_0, z_0)M0(x0,y0,z0) 、半径为 RRR 的球面方程为
(x−x0)2+(y−y0)2+(z−z0)=R2.(5-1)(x - x_0)^2 + (y - y_0)^2 + (z - z_0) = R^2. \tag{5-1} (x−x0)2+(y−y0)2+(z−z0)=R2.(5-1)
如果球心在原点,那么 x0=y0=z0=0x_0 = y_0 = z_0 = 0x0=y0=z0=0 ,从而球面方程为
x2+y2+z2=R2.x^2 + y^2 + z^2 = R^2. x2+y2+z2=R2.
二、旋转曲面
以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面叫做 旋转曲面 ,旋转曲线和定直线依次叫做旋转曲面的 母线 和 轴 。
设在 yOzyOzyOz 坐标面上有一已知曲线 CCC ,它的方程为
f(y,z)=0,f(y, z) = 0, f(y,z)=0,
把这曲线绕 zzz 轴旋转一周,就得到一个以 zzz 轴为轴的旋转曲面。它的方程可以求得如下:
设 M1(0,y1,z1)M_1(0, y_1, z_1)M1(0,y1,z1) 为曲线 CCC 上的任一点,则有
f(y1,z1)=0(5-2)f(y_1, z_1) = 0 \tag{5-2} f(y1,z1)=0(5-2)
当曲线 CCC 绕 zzz 轴旋转时,点 M1M_1M1 绕 zzz 轴转到另一点 M(x,y,z)M(x, y, z)M(x,y,z) ,这时 z=z1z = z_1z=z1 保持不变,且点 MMM 到 zzz 轴的距离
d=x2+y2=∣y1∣d = \sqrt{x^2 + y^2} = | y_1 | d=x2+y2=∣y1∣
将 z1=z,y1=±x2+y2z_1 = z, y_1 = \pm \sqrt{x^2 + y^2}z1=z,y1=±x2+y2 代入 (5−2)(5-2)(5−2) 式,就有
f(±x2+y2,z)=0,(5-3)f(\pm \sqrt{x^2 + y^2}, z) = 0, \tag{5-3} f(±x2+y2,z)=0,(5-3)
这就是所求旋转曲面的方程。
由此可知,在曲线 CCC 的方程 F(y,z)=0F(y, z) = 0F(y,z)=0 中将 yyy 改成 ±x2+y2\pm \sqrt{x^2 + y^2}±x2+y2 ,便得曲线 CCC 绕 zzz 轴旋转所成的旋转曲面的方程。
同理,曲线 CCC 绕 yyy 轴旋转所成的旋转曲面的方程为
f(y,±x2+z2)=0.(5-4)f(y, \pm \sqrt{x^2 + z^2}) = 0. \tag{5-4} f(y,±x2+z2)=0.(5-4)


三、柱面
一般地,直线 LLL 沿定曲线 CCC 平行移动形成的轨迹叫做 柱面 ,定曲线 CCC 叫做 柱面的准线 ,动直线 LLL 叫做 柱面的母线 。
一般地,只含 x,yx, yx,y 而缺 zzz 的方程 F(x,y)=0F(x, y) = 0F(x,y)=0 在空间直角坐标系中表示母线平行于 zzz 轴的柱面,其准线是 xOyxOyxOy 面上的曲线。
类似可知,只含 x,zx, zx,z 而缺 yyy 的方程 G(x,z)=0G(x, z) = 0G(x,z)=0 和只含 y,zy, zy,z 而缺 xxx 的方程 H(y,z)=0H(y, z) = 0H(y,z)=0 分别表示母线平行于 yyy 轴和 xxx 轴的柱面。
四、二次曲线
三元二次方程 F(x,y,z)=0F(x, y, z) = 0F(x,y,z)=0 所表示的曲面称为 二次曲面 ,而把平面称为 一次曲面 。
二次曲面有九种,适当选取空间直角坐标系,可得它们的标准方程。
1. 椭圆锥面 x2a2+y2b2=z2\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} = z^2a2x2+b2y2=z2
以垂直于 zzz 轴的平面 z=tz = tz=t 截此曲面,当 t=0t = 0t=0 时得一点 (0,0,0)(0, 0, 0)(0,0,0) ;当 t≠0t \neq 0t=0 时,得平面 z=tz = tz=t 上的椭圆
x2(at)2+y2(bt)2=1.\cfrac{x^2}{(at)^2} + \cfrac{y^2}{(bt)^2} = 1. (at)2x2+(bt)2y2=1.
当 ttt 变化时,上式表示一族长短轴比例不变的椭圆,当 ∣t∣|t|∣t∣ 从大到小并变为0时,这族椭圆从大到小并缩为一点。综合上述讨论,可得椭圆锥面的形状如下图(图8-48)所示.
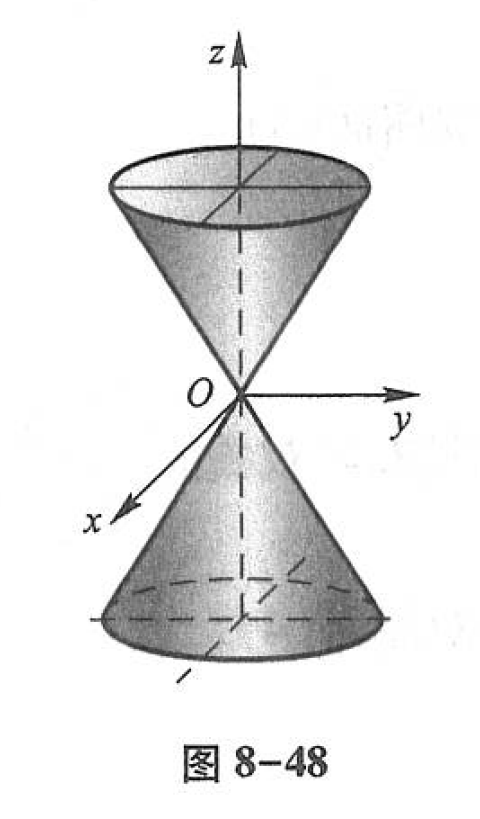
平面 z=tz = tz=t 与曲面 F(x,y,z)=0F(x, y, z) = 0F(x,y,z)=0 的交线称为 截痕 。通过综合截痕的变化来了解曲面形状的方法称为 截痕法 。
还可以用伸缩变形的方法来得出椭圆锥面的形状。
先说明 xOyxOyxOy 平面上的图形伸缩变形的方法。在 xOyxOyxOy 平面上,把点 M(x,y)M(x, y)M(x,y) 变为点 M′(x,λy)M'(x, \lambda y)M′(x,λy) ,从而把点 MMM 的轨迹 CCC 变为点 M′M'M′ 的轨迹 C′C'C′ ,称为把图形 CCC 沿 yyy 轴方向伸缩 λ\lambdaλ 倍变成图形 C′C'C′ 。假如 CCC 为曲线 F(x,y)=0F(x, y) = 0F(x,y)=0 ,点 M(x1,y1)∈CM(x_1, y_1) \in CM(x1,y1)∈C ,点 MMM 变为点 M′(x2,y2)M'(x_2, y_2)M′(x2,y2) ,其中 x2=x1,y2=λy1x_2 = x_1, y_2 = \lambda y_1x2=x1,y2=λy1 ,即 x1=x2,y1=1λy2x_1 = x_2, y_1 = \cfrac{1}{\lambda} y_2x1=x2,y1=λ1y2 ,因点 M∈CM \in CM∈C ,有 F(x1,y1)=0F(x_1, y_1) = 0F(x1,y1)=0 ,故 F(x2,1λy2)=0F \left(x_2, \cfrac{1}{\lambda} y_2 \right) = 0F(x2,λ1y2)=0 ,因此点 M′(x2,y2)M'(x_2, y_2)M′(x2,y2) 的轨迹 C′C'C′ 的方程为 F(x,1λy)=0F \left( x, \cfrac{1}{\lambda} y \right) = 0F(x,λ1y)=0 。例如把圆 x2+y2=a2x^2 + y_2 = a^2x2+y2=a2 沿 yyy 轴方向伸缩 ba\cfrac{b}{a}ab 倍,就变为椭圆 x2a2+y2b2=1\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} = 1a2x2+b2y2=1 。
类似地,把空间图形沿 yyy 轴方向伸缩 ba\cfrac{b}{a}ab 倍,圆锥面 x2+y2a2=z2\cfrac{x^2 + y^2}{a^2} = z^2a2x2+y2=z2 就变为椭圆锥面 x2a2+y2b2=z2\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} = z^2a2x2+b2y2=z2 。
利用圆锥面(旋转曲面)的伸缩变形来得出椭圆锥面的形状,这种方法是研究曲面形状的一种较方便的方法。
2.椭球面 x2a2+y2b2+z2c2=1\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} + \cfrac{z^2}{c^2} = 1a2x2+b2y2+c2z2=1
把 zOxzOxzOx 面上的椭圆 x2a2+z2c2=1\cfrac{x^2}{a^2} + \cfrac{z^2}{c^2} = 1a2x2+c2z2=1 绕 zzz 轴旋转,所得的曲面称为 旋转椭球面 ,其方程为
x2+y2a2+z2c2=1\cfrac{x^2 + y^2}{a^2} + \cfrac{z^2}{c^2} = 1 a2x2+y2+c2z2=1
再把旋转椭球面沿 yyy 轴方向伸缩 ba\cfrac{b}{a}ab 倍,便得椭球面 (2)(2)(2) 的形状如图8-50所示。
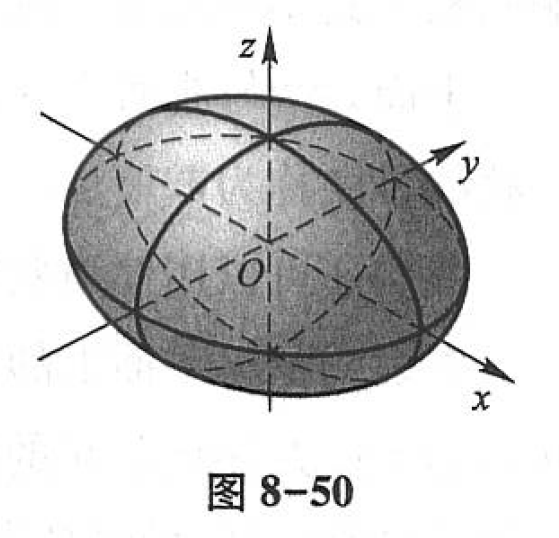
当 a=b=ca=b=ca=b=c 时,椭球面 (2)(2)(2) 成为 x2+y2+z2=a2x^2 + y^2 + z^2 = a^2x2+y2+z2=a2 ,这时球心在原点、半径为 aaa 的球面。显然,球面是旋转椭球面的特殊情形,旋转椭球面是椭球面的特殊情形。把球面 x2+y2+z2=a2x^2 + y^2 + z^2 = a^2x2+y2+z2=a2 沿 zzz 轴伸缩 ca\cfrac{c}{a}ac 倍,即得旋转椭球面 x2+y2a2+z2c2=1\cfrac{x^2 + y^2}{a^2} + \cfrac{z^2}{c^2} = 1a2x2+y2+c2z2=1 ;再沿 yyy 轴方向伸缩 ba\cfrac{b}{a}ab 倍,即得椭球面 (2)(2)(2) 。
3.单叶双曲面 x2a2+y2b2−z2c2=1\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} - \cfrac{z^2}{c^2} = 1a2x2+b2y2−c2z2=1
把 zOxzOxzOx 面上的双曲线 x2a2−z2c2=1\cfrac{x^2}{a^2} - \cfrac{z^2}{c^2} = 1a2x2−c2z2=1 绕 zzz 轴旋转,得旋转单叶双曲面 x2+y2a2−z2c2=1\cfrac{x^2 + y^2}{a^2} - \cfrac{z^2}{c^2} = 1a2x2+y2−c2z2=1 ,把此旋转曲面沿 yyy 轴方向伸缩 ba\cfrac{b}{a}ab 倍,即得单叶双曲面 (3)(3)(3) 。
4.双叶双曲面 x2a2−y2b2−z2c2=1\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} - \cfrac{z^2}{c^2} = 1a2x2−b2y2−c2z2=1
把 zOxzOxzOx 面上的双曲线 x2a2−z2c2=1\cfrac{x^2}{a^2} - \cfrac{z^2}{c^2} = 1a2x2−c2z2=1 绕 xxx 轴旋转,得旋转双叶双曲面 x2a2−y2+z2c2=1\cfrac{x^2}{a^2} - \cfrac{y^2 + z^2}{c^2} = 1a2x2−c2y2+z2=1 ,把此旋转曲面沿 yyy 轴方向伸缩 bc\cfrac{b}{c}cb 倍,即得双叶双曲面 (4)(4)(4) 。
5.椭圆抛物面 x2a2+y2b2=z\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} = za2x2+b2y2=z
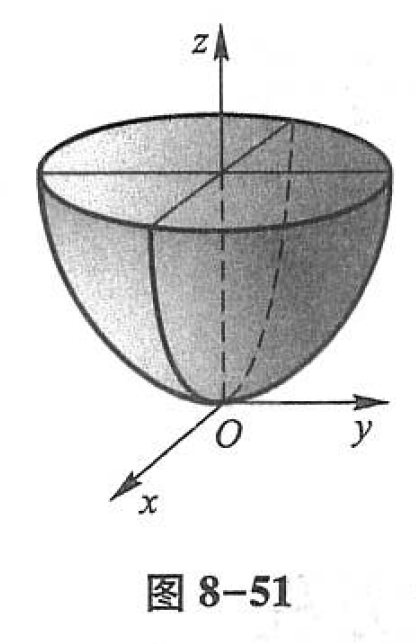
把 zOxzOxzOx 面上的抛物线 x2a2=z\cfrac{x^2}{a^2} = za2x2=z 绕 zzz 轴旋转,所得曲面叫做 旋转抛物面 ,如图8-51所示。把此旋转曲面沿 yyy 轴方向伸缩 ba\cfrac{b}{a}ab 倍,即得椭圆抛物面 (5)(5)(5) 。
6.双曲抛物面 x2a2−y2b2=z\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} = za2x2−b2y2=z
双曲抛物面又称 马鞍面 ,我们用截痕法来讨论它的形状。
用平面 x=tx = tx=t 截此曲面,所得截痕 lll 为平面 x=tx = tx=t 上的抛物线
−y2b2=z−t2a2,-\cfrac{y^2}{b^2} = z - \cfrac{t^2}{a^2} , −b2y2=z−a2t2,
此抛物线开口朝下,其顶点坐标为
x=t,y=0,z=t2a2x = t, \quad y = 0, \quad z = \cfrac{t^2}{a^2} x=t,y=0,z=a2t2
当 ttt 变化时,lll 的形状不变,位置只作平移,而 lll 的顶点的轨迹 LLL 为平面 y=0y = 0y=0 上的抛物线
z=x2a2.z = \cfrac{x^2}{a^2}. z=a2x2.
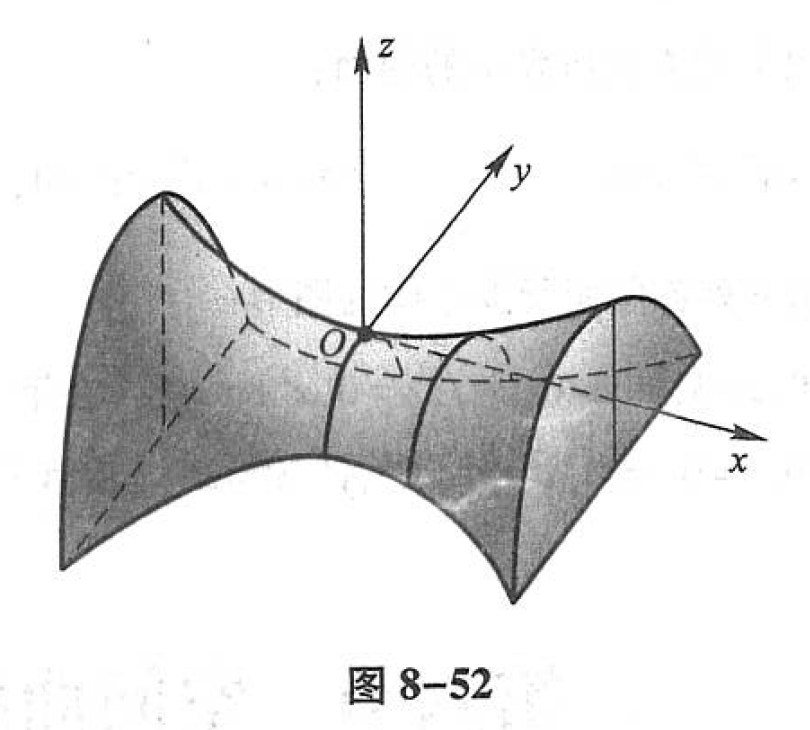
因此,以 lll 为母线,LLL 为准线,母线 lll 的顶点在准线 LLL 上滑动,且母线作平行移动,这样得到的曲面便是双曲抛物面 (6)(6)(6) ,如图8-52所示。
还有三种二次曲面是以三种二次曲线为准线的柱面
x2a2+y2b2=1,x2a2−y2b2=1,x2=ay.\cfrac{x^2}{a^2} + \cfrac{y^2}{b^2} = 1, \quad \cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} = 1, \quad x^2 = ay. a2x2+b2y2=1,a2x2−b2y2=1,x2=ay.
依次称为 椭球柱面 、双曲柱面 、抛物柱面 。
原文链接:高等数学 8.5 曲面及其方程
