【数据结构】深入理解双向链表:结构、实现与对比分析
文章目录
- 一、链表的分类
- 常用链表类型
- (1)无头单向非循环链表(单链表)
- (2)带头双向循环链表(双向链表)
- 二、双向链表的结构
- 三、双向链表的实现
- 1. 节点结构定义
- 2. 主要操作函数
- (1) 初始化函数(LTInit)
- (2)销毁函数(LTDestroy)
- (3)打印函数(LTPrint)
- (4)判断空表函数(LTEmpty)
- (5)尾部插入函数(LTPushBack)
- (6)尾部删除函数(LTPopBack)
- (7)头部插入函数(LTPushFront)
- (8)头部删除函数(LTPopFront)
- (9)指定位置后插入函数(LTInsert)
- (10)指定位置删除函数(LTErase)
- (11) 查找函数(LTFind)
- 四、顺序表和双向链表的优缺点分析
一、链表的分类
链表的结构多样,可通过以下三个维度组合出 8 种类型:
- 方向
-
单向:只能从一个方向遍历
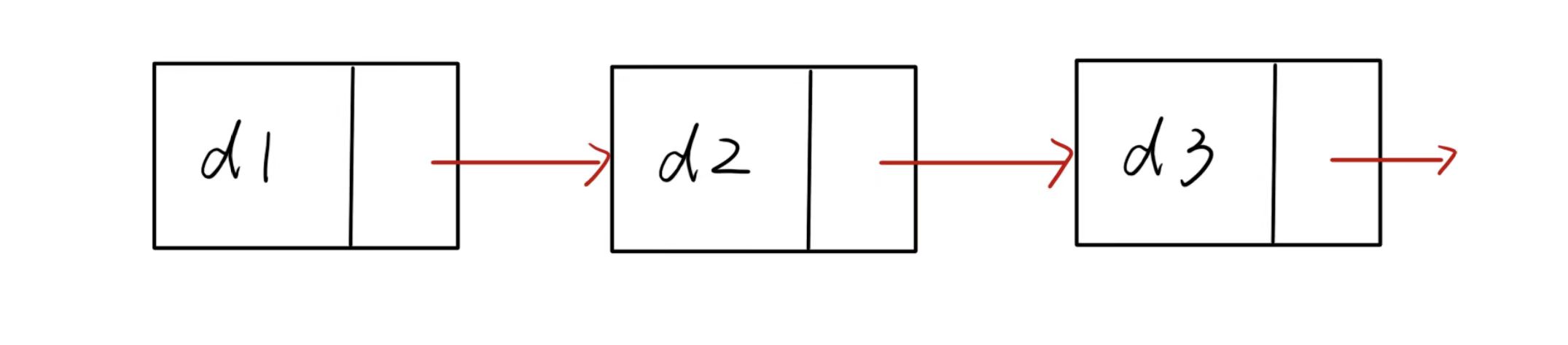
-
双向:可以从两个方向遍历
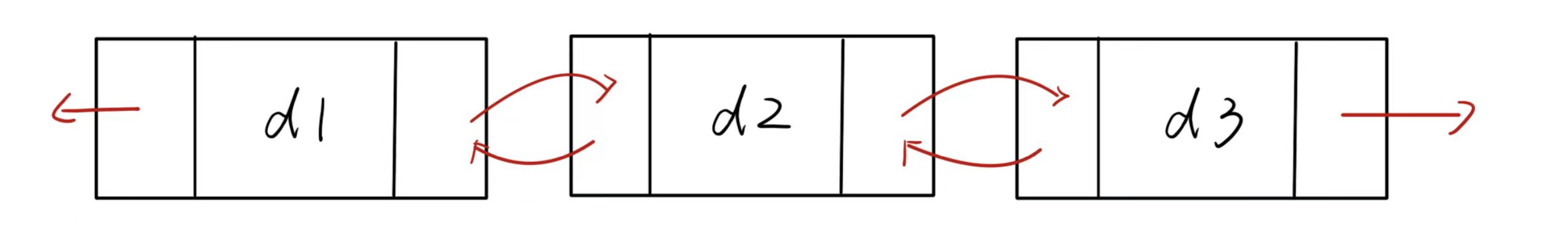
-
- 头部:
-
带头(有哨兵位)

-
不带头

-
- 循环性:
-
循环
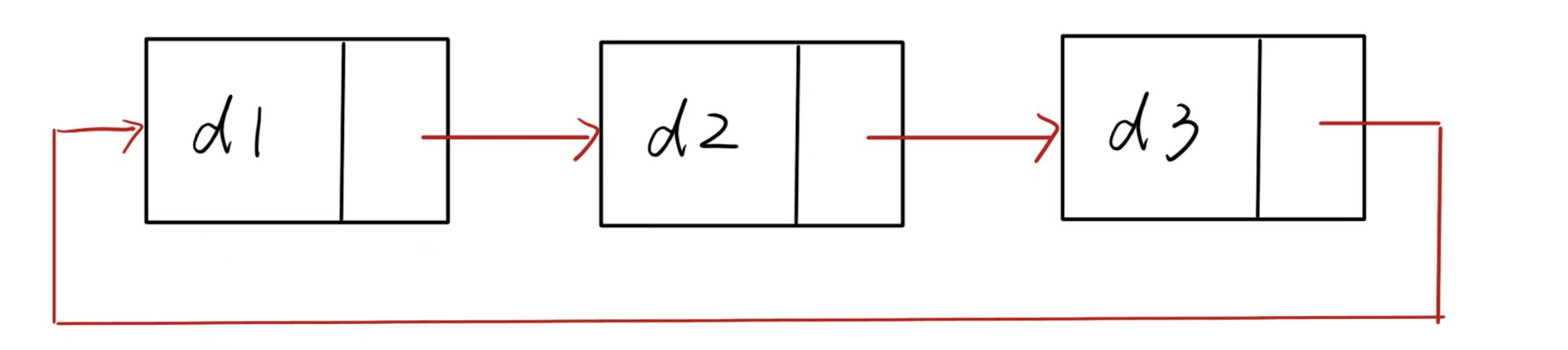
-
非循环

-
常用链表类型
(1)无头单向非循环链表(单链表)
- 特点: 结构简单,无哨兵位节点,最后一个节点的 next 为 NULL
- 应用场景: 多作为其他数据结构的子结构(如哈希桶、图的邻接表),笔试面试高频考点
(2)带头双向循环链表(双向链表)
- 特点: 包含哨兵位头节点,每个节点有 prev 和 next 两个指针,尾节点的 next 指向头节点
- 优势: 操作统一(无需特殊处理空链表或首尾节点),实现简单
- 应用场景: 单独存储数据(如 STL 中的 list)
二、双向链表的结构
双向链表中,我们重点关注的是带头双向循环链表。这里的“带头”需要特别说明,它和单链表中我们常说的“头节点”不是一个概念。在单链表阶段,我们对“头节点”的称呼其实并不严谨,为了便于理解才那样称呼。而带头双向循环链表中的“头节点”,实际是“哨兵位”。
“哨兵位”节点不存储任何有效元素,它就像一个站在那里“放哨”的节点,其存在的最大意义是避免在遍历循环链表时出现死循环。有了这个哨兵位,我们在进行链表的遍历等操作时,就有了一个明确的起点和终点判断依据,大大降低了出错的概率。
三、双向链表的实现
1. 节点结构定义
首先,我们需要定义双向链表的节点结构。每个节点不仅要存储数据,还要有两个指针,分别指向它的前一个节点和后一个节点,具体定义如下:
typedef int LTDataType;
typedef struct ListNode
{struct ListNode* next; // 指针保存下一个节点的地址struct ListNode* prev; // 指针保存前一个节点的地址LTDataType data; // 存储的数据
}LTNode;
2. 主要操作函数
(1) 初始化函数(LTInit)
初始化函数用于创建双向链表的哨兵位节点,并构建带头双向循环的初始结构。
实现思路:
- 动态开辟一个哨兵位节点。
- 让哨兵位节点的prev和next指针都指向自身,形成循环结构。
LTNode* LTInit()
{LTNode* phead = (LTNode*)malloc(sizeof(LTNode));if (phead == NULL){perror("malloc fail");exit(-1);}phead->next = phead;phead->prev = phead;return phead;
}
该函数返回初始化好的哨兵位节点,为后续操作提供基础。
(2)销毁函数(LTDestroy)
销毁函数用于释放链表中所有节点(包括哨兵位)的内存,避免内存泄漏。
实现思路:
- 先判断链表是否为空,若为空则直接释放哨兵位。
- 若不为空,通过遍历找到每一个节点并释放,最后释放哨兵位。
void LTDestroy(LTNode* phead)
{assert(phead);LTNode* cur = phead->next;while (cur != phead){LTNode* next = cur->next;free(cur);cur = next;}free(phead);
}
通过循环遍历释放除哨兵位外的所有节点,最后释放哨兵位,完成链表的销毁。
(3)打印函数(LTPrint)
打印函数用于输出链表中所有的有效元素。
实现思路:
- 从哨兵位的下一个节点开始遍历。
- 遍历至重新回到哨兵位时停止,依次打印每个节点的数据。
void LTPrint(LTNode* phead)
{assert(phead);LTNode* cur = phead->next;printf("哨兵位<->");while (cur != phead){printf("%d<->", cur->data);cur = cur->next;}printf("\n");
}
打印时清晰展示节点间的双向关系,便于观察链表结构。
(4)判断空表函数(LTEmpty)
判断空表函数用于检查链表是否为空(即除哨兵位外无其他节点)。
实现思路:
- 若哨兵位的next指针指向自身,则链表为空。
bool LTEmpty(LTNode* phead)
{assert(phead);return phead->next == phead;
}
通过简单的指针判断,高效得出链表是否为空的结果。
(5)尾部插入函数(LTPushBack)
尾部插入函数用于在链表的尾部添加一个新节点。
实现思路:
- 找到链表的尾节点(哨兵位的prev指针所指节点)。
- 建立新节点与尾节点、哨兵位之间的双向链接。
void LTPushBack(LTNode* phead, LTDataType x)
{assert(phead);LTNode* newnode = BuyLTNode(x);LTNode* tail = phead->prev;tail->next = newnode;newnode->prev = tail;newnode->next = phead;phead->prev = newnode;
}
其中BuyLTNode为创建新节点的辅助函数,通过调整指针完成尾部插入,时间复杂度为O(1)。
(6)尾部删除函数(LTPopBack)
尾部删除函数用于移除链表的最后一个节点。
实现思路:
- 先判断链表是否为空,为空则无法删除。
- 找到尾节点及其前一个节点,通过调整指针解除尾节点的链接并释放其内存。
void LTPopBack(LTNode* phead)
{assert(phead);assert(!LTEmpty(phead));LTNode* tail = phead->prev;LTNode* prev = tail->prev;prev->next = phead;phead->prev = prev;free(tail);
}
删除操作只需修改相关指针,无需搬移元素,效率较高。
(7)头部插入函数(LTPushFront)
头部插入函数用于在哨兵位之后添加新节点。
实现思路:
- 找到哨兵位的下一个节点(原头节点)。
- 建立新节点与哨兵位、原头节点之间的双向链接。
void LTPushFront(LTNode* phead, LTDataType x)
{assert(phead);LTNode* newnode = BuyLTNode(x);LTNode* first = phead->next;phead->next = newnode;newnode->prev = phead;newnode->next = first;first->prev = newnode;
}
利用双向链表的指针特性,快速完成头部插入操作。
(8)头部删除函数(LTPopFront)
头部删除函数用于移除哨兵位之后的第一个节点。
实现思路:
- 先判断链表是否为空,为空则无法删除。
- 找到原头节点及其下一个节点,调整指针解除原头节点的链接并释放其内存。
void LTPopFront(LTNode* phead)
{assert(phead);assert(!LTEmpty(phead));LTNode* first = phead->next;LTNode* second = first->next;phead->next = second;second->prev = phead;free(first);
}
(9)指定位置后插入函数(LTInsert)
实现思路:
- 找到pos节点的下一个节点。
- 建立新节点与pos节点、pos下一个节点之间的双向链接。
void LTInsert(LTNode* pos, LTDataType x)
{assert(pos);LTNode* newnode = BuyLTNode(x);LTNode* next = pos->next;pos->next = newnode;newnode->prev = pos;newnode->next = next;next->prev = newnode;
}
该函数为灵活插入提供了支持,是实现头插、尾插的基础。
(10)指定位置删除函数(LTErase)
实现思路:
- 找到pos节点的前一个和后一个节点。
- 调整这两个节点的指针,解除与pos节点的链接并释放pos节点的内存。
void LTErase(LTNode* pos)
{assert(pos);LTNode* prev = pos->prev;LTNode* next = pos->next;prev->next = next;next->prev = prev;free(pos);
}
通过该函数可方便地实现头删、尾删等操作。
(11) 查找函数(LTFind)
查找函数用于在链表中寻找数据为x的节点。
实现思路:
- 从哨兵位的下一个节点开始遍历。
- 若找到数据为x的节点则返回该节点,遍历结束仍未找到则返回NULL。
LTNode* LTFind(LTNode* phead, LTDataType x)
{assert(phead);LTNode* cur = phead->next;while (cur != phead){if (cur->data == x){return cur;}cur = cur->next;}return NULL;
}
查找操作需要遍历链表,时间复杂度为O(N)。
以上这些操作函数充分利用了双向链表的结构特点,使得插入和删除等操作无需像顺序表那样进行大量数据搬移,大大提高了在频繁进行这类操作场景下的效率。
四、顺序表和双向链表的优缺点分析
为了更好地理解双向链表的适用场景,我们将它与顺序表进行对比分析:
| 不同点 | 顺序表 | 链表(这里主要指双向链表) |
|---|---|---|
| 存储空间上 | 物理上一定连续 | 逻辑上连续,但物理上不一定连续 |
| 随机访问 | 支持,时间复杂度为O(1) | 不支持,时间复杂度为O(N) |
| 任意位置插入或者删除元素 | 可能需要搬移元素,效率低,时间复杂度为O(N) | 只需修改指针指向,效率高 |
| 插入相关 | 动态顺序表在空间不够时需要扩容 | 没有容量的概念,不需要扩容 |
| 应用场景 | 适用于元素高效存储且需要频繁访问的场景 | 适用于任意位置插入和删除操作频繁的场景 |
通过以上对比可以看出,顺序表和双向链表各有其优势和劣势。在实际开发中,我们需要根据具体的应用场景来选择合适的数据结构。如果需要频繁地访问元素,那么顺序表是更好的选择;如果需要频繁地进行插入和删除操作,尤其是在任意位置进行这些操作,那么双向链表会更合适。
