《算法导论》第 26 章 - 最大流
思维导图

引言
最大流问题是网络流理论中的核心问题,在交通调度、资源分配、任务指派等领域有着广泛应用。本章将详细讲解《算法导论》第 26 章中的最大流相关算法,包括 Ford-Fulkerson 方法、Edmonds-Karp 算法、推送重贴标签算法等,并提供完整可运行的 C++ 代码实现。
26.1 流网络
基本概念
流网络是一个有向图 G=(V,E),具有以下特性:
- 有一个唯一的源点 s
- 有一个唯一的汇点 t
- 每条边 (u,v) 有一个非负的容量 c (u,v) ≥ 0
- 流是一个实值函数 f:V×V→R,满足容量限制和流量守恒
流的性质
- 容量限制:对所有 u,v∈V,0 ≤ f (u,v) ≤ c (u,v)
- 反对称性:对所有 u,v∈V,f (u,v) = -f (v,u)
- 流量守恒:对所有 u∈V-{s,t},Σf (u,v) = 0(v∈V)
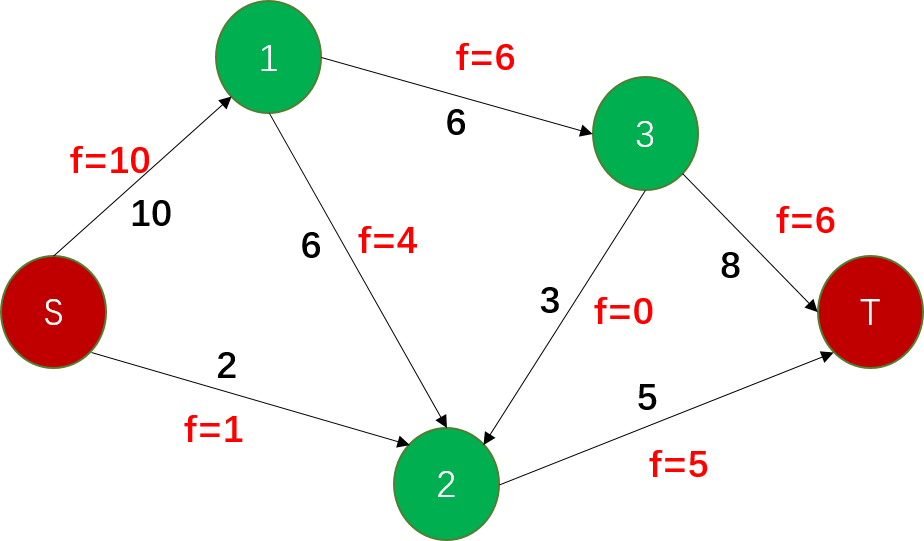
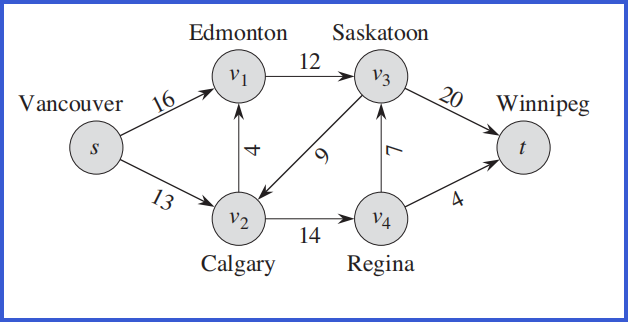
流网络图示
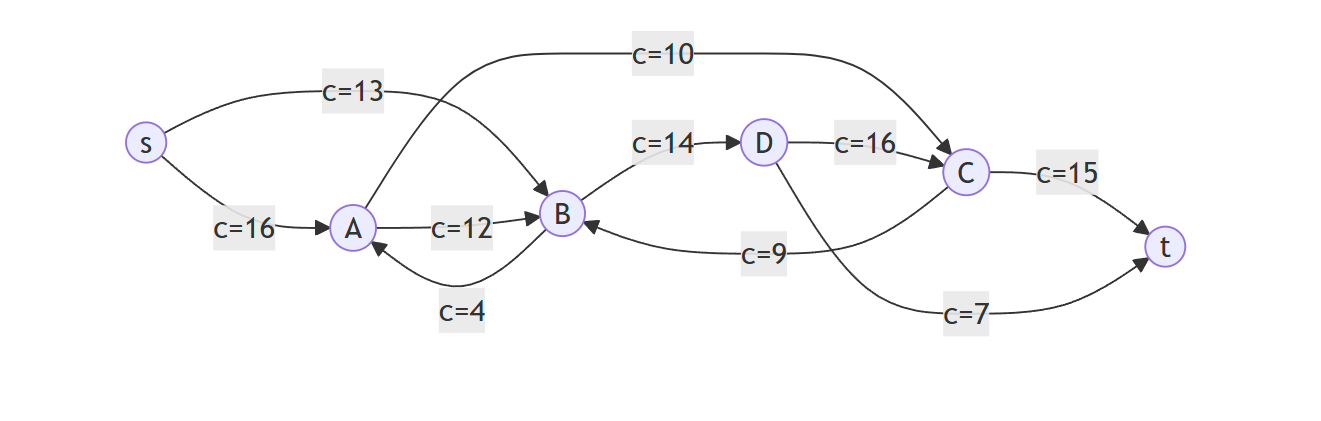
残量网络与增广路径
- 残量网络:由可以容纳更多流的边组成的网络
- 增广路径:残量网络中从源点到汇点的路径,可以沿此路径增加流量
26.2 Ford-Fulkerson 方法
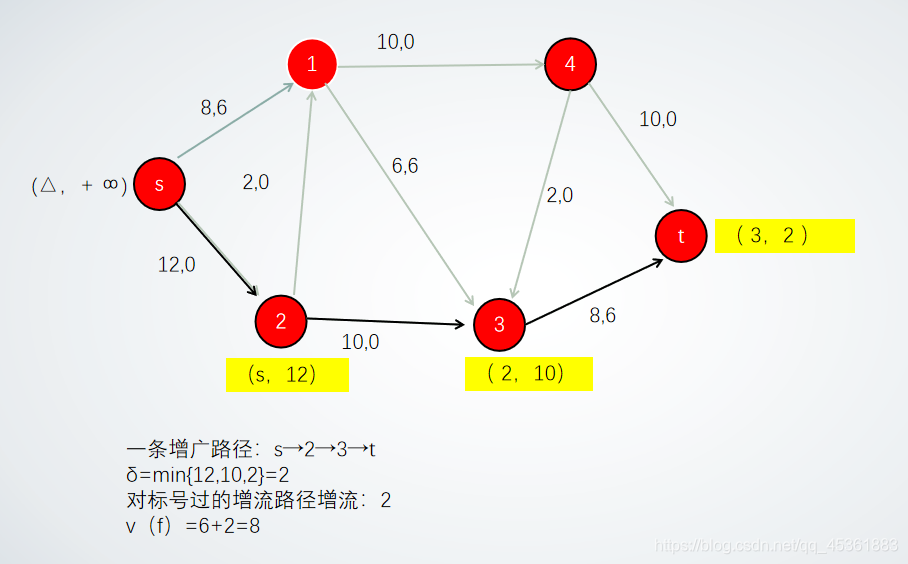
基本思想
Ford-Fulkerson 方法是一种迭代方法,其基本思想是:
- 初始化流为 0
- 寻找一条增广路径
- 沿增广路径增加尽可能多的流量
- 重复步骤 2-3,直到没有增广路径为止
Edmonds-Karp 算法
Edmonds-Karp 算法是 Ford-Fulkerson 方法的一种实现,使用 BFS 来寻找最短的增广路径(以边数为度量)。
算法流程图
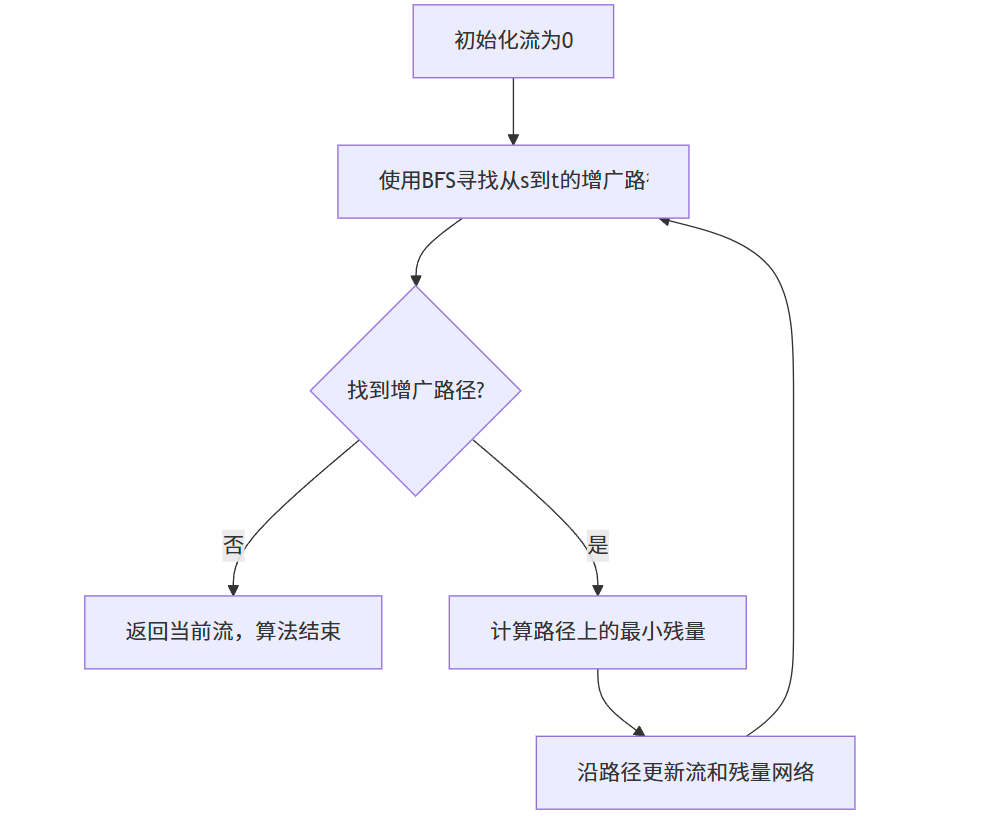
代码实现
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;// 表示边的结构
struct Edge {int to, rev; // rev是反向边在邻接表中的索引int capacity; // 剩余容量Edge(int t, int r, int c) : to(t), rev(r), capacity(c) {}
};class MaxFlow {
private:vector<vector<Edge>> graph; // 图的邻接表表示vector<int> parent; // BFS中记录路径vector<int> parentEdge; // 记录到达节点的边索引// BFS寻找增广路径bool bfs(int s, int t) {fill(parent.begin(), parent.end(), -1);fill(parentEdge.begin(), parentEdge.end(), -1);queue<int> q;q.push(s);parent[s] = s; // 源点的父节点是自身while (!q.empty()) {int u = q.front();q.pop();// 遍历所有邻边for (int i = 0; i < graph[u].size(); ++i) {Edge &e = graph[u][i];// 如果找到未访问且有剩余容量的节点if (parent[e.to] == -1 && e.capacity > 0) {parent[e.to] = u;parentEdge[e.to] = i;q.push(e.to);// 到达汇点,返回trueif (e.to == t) {return true;}}}}return false; // 未找到增广路径}public:// 构造函数,初始化图MaxFlow(int n) : graph(n), parent(n), parentEdge(n) {}// 添加边void addEdge(int from, int to, int capacity) {// 添加正向边graph[from].emplace_back(to, graph[to].size(), capacity);// 添加反向边,初始容量为0graph[to].emplace_back(from, graph[from].size() - 1, 0);}// 计算最大流int edmondsKarp(int s, int t) {int maxFlow = 0;// 不断寻找增广路径while (bfs(s, t)) {int pathFlow = INT_MAX;// 找到路径上的最小残量for (int v = t; v != s; v = parent[v]) {int u = parent[v];Edge &e = graph[u][parentEdge[v]];pathFlow = min(pathFlow, e.capacity);}// 更新残量网络for (int v = t; v != s; v = parent[v]) {int u = parent[v];Edge &e = graph[u][parentEdge[v]];e.capacity -= pathFlow;graph[v][e.rev].capacity += pathFlow;}maxFlow += pathFlow;}return maxFlow;}
};// 示例用法
int main() {// 创建一个有6个节点(0-5)的图MaxFlow mf(6);// 添加边,容量mf.addEdge(0, 1, 16);mf.addEdge(0, 2, 13);mf.addEdge(1, 2, 10);mf.addEdge(1, 3, 12);mf.addEdge(2, 1, 4);mf.addEdge(2, 4, 14);mf.addEdge(3, 2, 9);mf.addEdge(3, 5, 20);mf.addEdge(4, 3, 7);mf.addEdge(4, 5, 4);// 计算从0到5的最大流cout << "最大流为: " << mf.edmondsKarp(0, 5) << endl;return 0;
}
代码说明
上述代码实现了 Edmonds-Karp 算法,主要包含以下部分:
Edge结构体:表示图中的边,包含目标节点、反向边索引和剩余容量MaxFlow类:封装了最大流算法的实现bfs方法:寻找从源点到汇点的增广路径addEdge方法:向图中添加边edmondsKarp方法:实现 Edmonds-Karp 算法,计算最大流
26.3 最大二分匹配
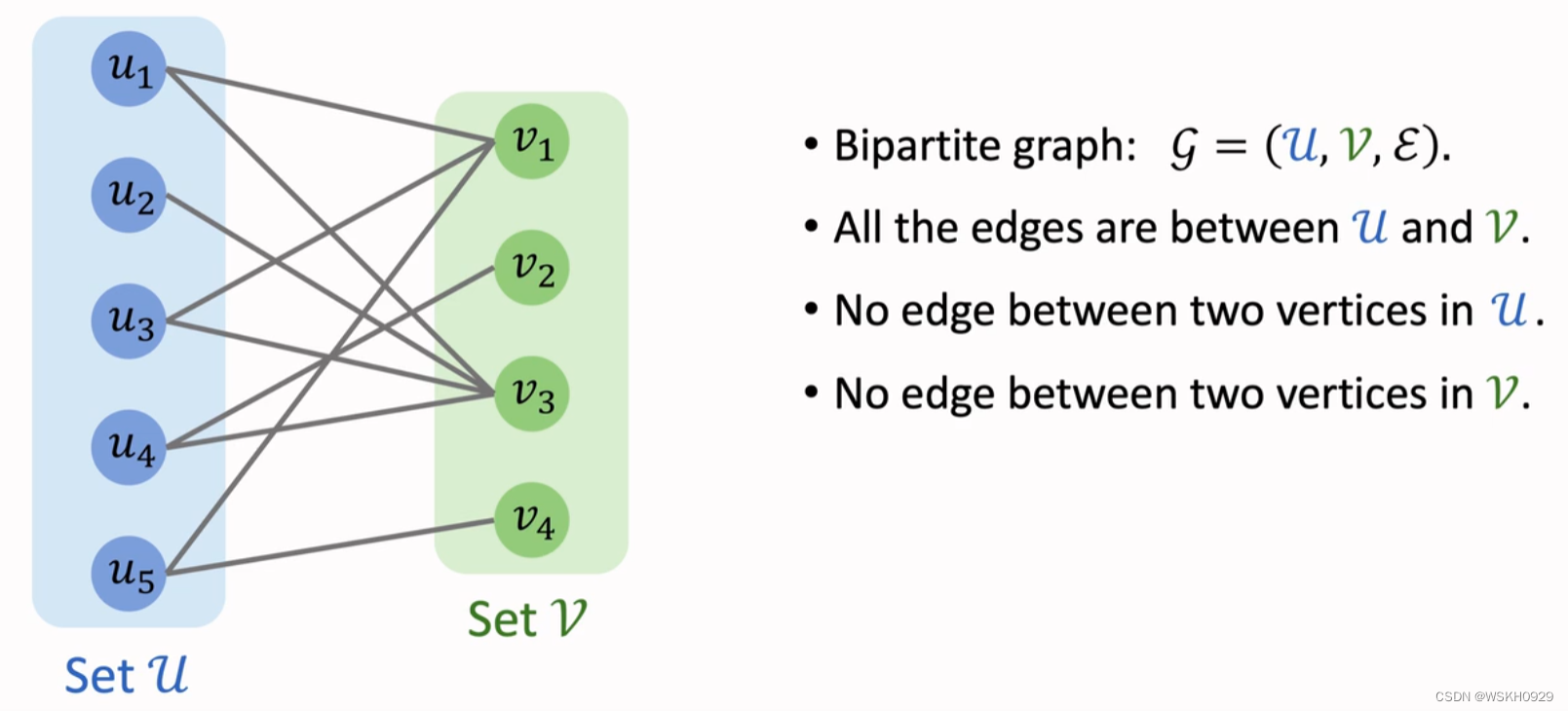
二分图与匹配
二分图是一种特殊的图,其顶点可以分为两个不相交的集合 U 和 V,且图中的每条边都连接 U 中的一个顶点和 V 中的一个顶点。
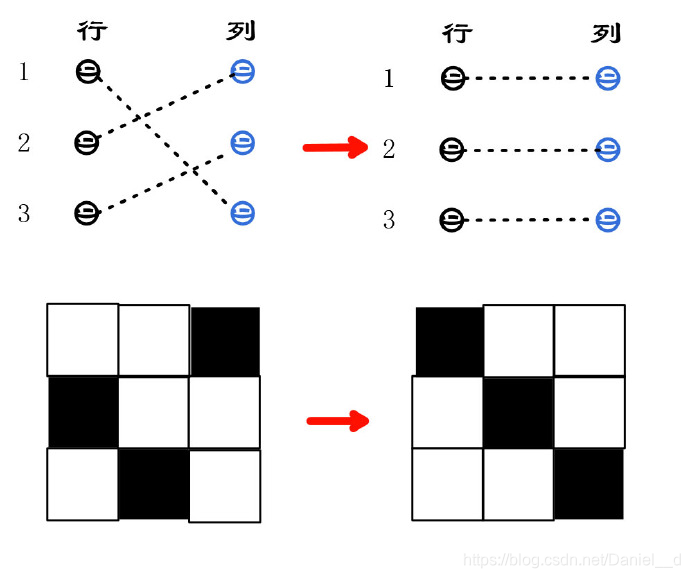
匹配是二分图中的一组边,其中任意两条边都不共享顶点。最大匹配是包含边数最多的匹配。
转化为最大流问题
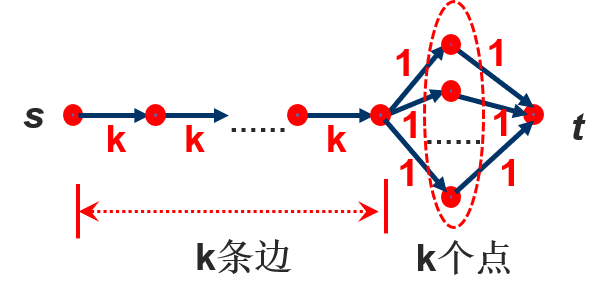
最大二分匹配问题可以转化为最大流问题:
- 创建一个源点 s 和一个汇点 t
- 从 s 向 U 中的每个顶点添加一条容量为 1 的边
- 从 V 中的每个顶点向 t 添加一条容量为 1 的边
- 对于二分图中 U 到 V 的每条边,添加一条容量为 1 的边
- 计算从 s 到 t 的最大流,其值等于最大匹配的大小
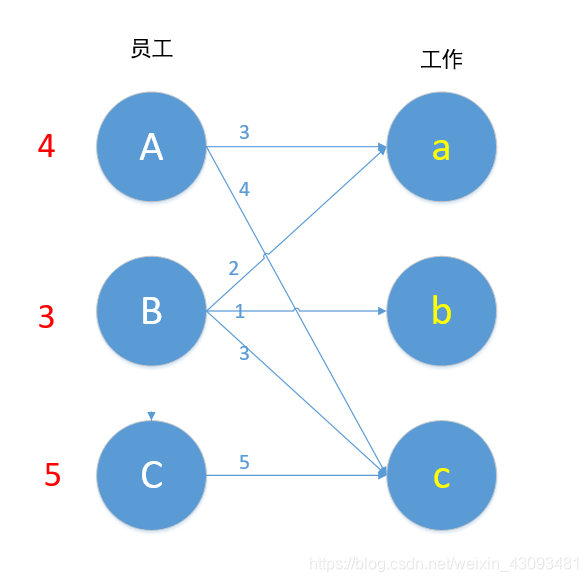
二分图匹配转化示意图
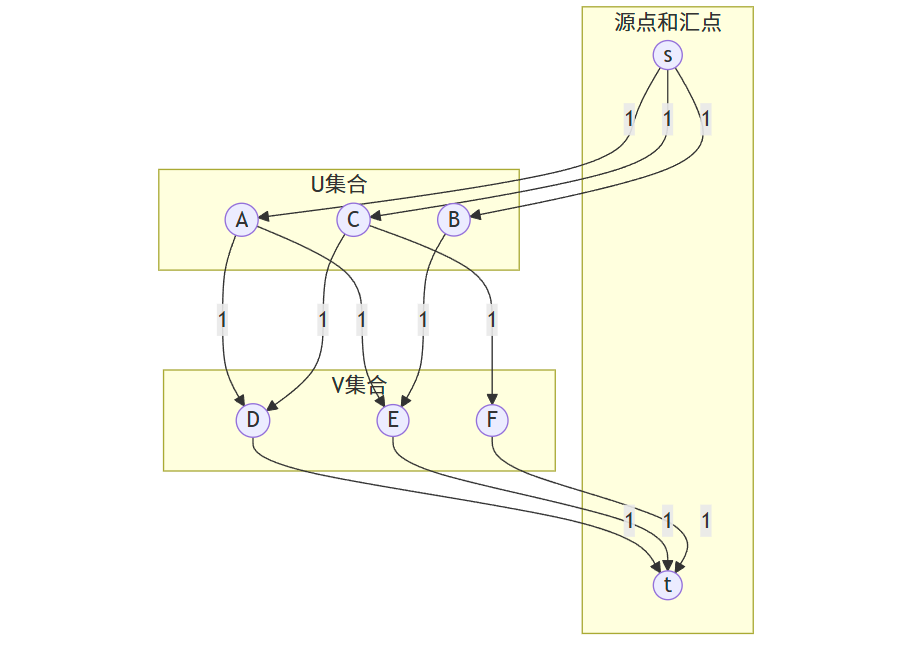
代码实现
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;struct Edge {int to, rev, capacity;Edge(int t, int r, int c) : to(t), rev(r), capacity(c) {}
};class BipartiteMatching {
private:vector<vector<Edge>> graph;vector<int> parent;vector<int> parentEdge;int n, m; // U集合和V集合的大小int s, t; // 源点和汇点bool bfs() {fill(parent.begin(), parent.end(), -1);fill(parentEdge.begin(), parentEdge.end(), -1);queue<int> q;q.push(s);parent[s] = s;while (!q.empty()) {int u = q.front();q.pop();for (int i = 0; i < graph[u].size(); ++i) {Edge &e = graph[u][i];if (parent[e.to] == -1 && e.capacity > 0) {parent[e.to] = u;parentEdge[e.to] = i;q.push(e.to);if (e.to == t) {return true;}}}}return false;}public:// n: U集合大小, m: V集合大小BipartiteMatching(int n, int m) : n(n), m(m) {// 总节点数: n + m + 2 (U + V + s + t)int totalNodes = n + m + 2;s = 0;t = n + m + 1;graph.resize(totalNodes);parent.resize(totalNodes);parentEdge.resize(totalNodes);// 添加源点到U的边for (int i = 1; i <= n; ++i) {addEdge(s, i, 1);}// 添加V到汇点的边for (int i = n + 1; i <= n + m; ++i) {addEdge(i, t, 1);}}// 添加U中节点u到V中节点v的边 (u: 1~n, v: 1~m)void addEdgeUV(int u, int v) {int uNode = u;int vNode = n + v;addEdge(uNode, vNode, 1);}// 添加边的内部实现void addEdge(int from, int to, int capacity) {graph[from].emplace_back(to, graph[to].size(), capacity);graph[to].emplace_back(from, graph[from].size() - 1, 0);}// 计算最大匹配int maxMatching() {int flow = 0;while (bfs()) {int pathFlow = INT_MAX;// 找到路径上的最小残量for (int v = t; v != s; v = parent[v]) {int u = parent[v];Edge &e = graph[u][parentEdge[v]];pathFlow = min(pathFlow, e.capacity);}// 更新残量网络for (int v = t; v != s; v = parent[v]) {int u = parent[v];Edge &e = graph[u][parentEdge[v]];e.capacity -= pathFlow;graph[v][e.rev].capacity += pathFlow;}flow += pathFlow;}return flow;}// 打印匹配结果void printMatching() {cout << "匹配结果:" << endl;for (int u = 1; u <= n; ++u) {for (Edge &e : graph[u]) {// 如果边从U到V且容量为0,说明该边被使用if (e.to != s && e.capacity == 0 && e.to != t) {int v = e.to - n; // 转换回V集合中的编号cout << "U" << u << " -> V" << v << endl;}}}}
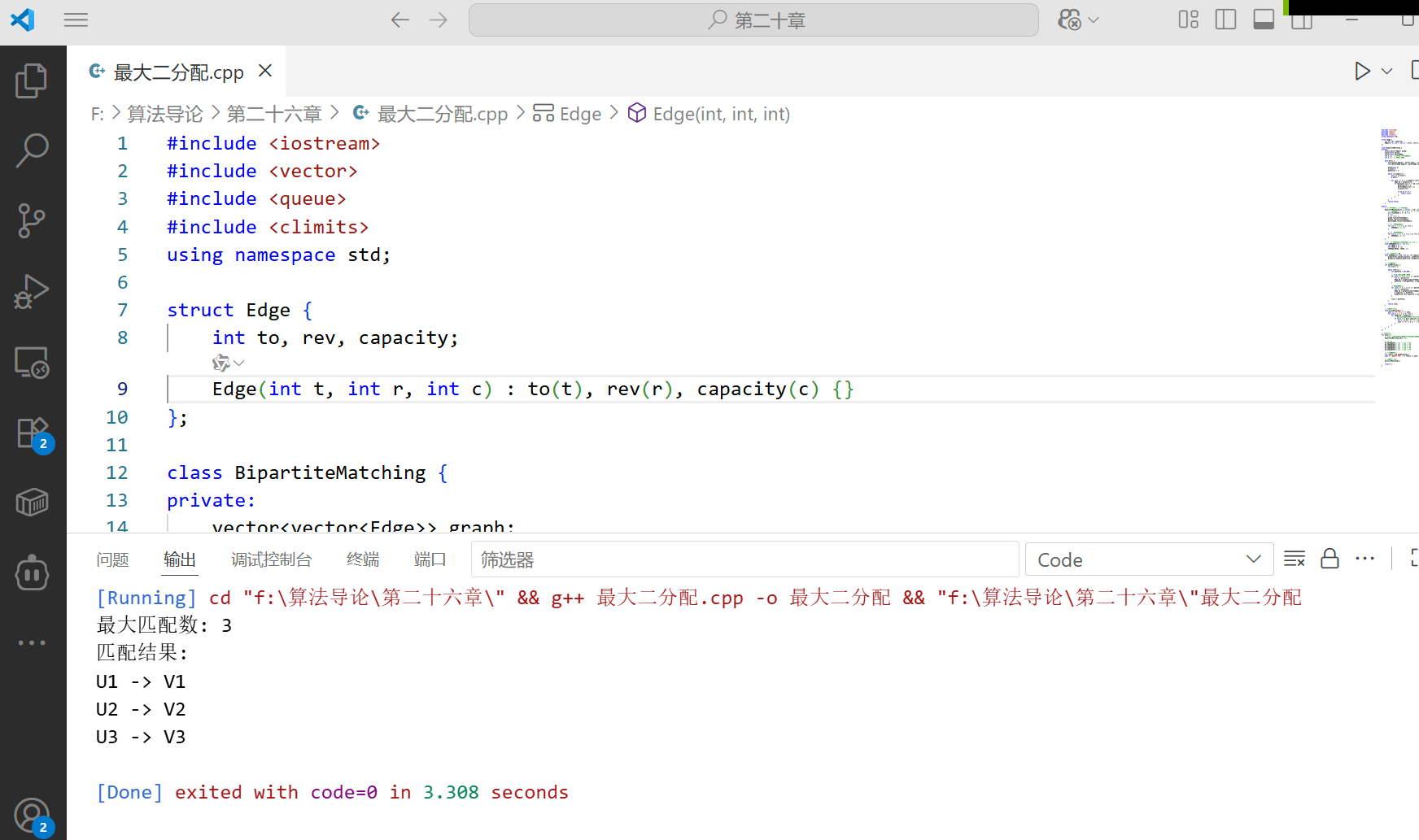
};// 示例用法
int main() {// 创建一个U集合有3个节点,V集合有3个节点的二分图BipartiteMatching bm(3, 3);// 添加边bm.addEdgeUV(1, 1); // U1 -> V1bm.addEdgeUV(1, 2); // U1 -> V2bm.addEdgeUV(2, 2); // U2 -> V2bm.addEdgeUV(3, 1); // U3 -> V1bm.addEdgeUV(3, 3); // U3 -> V3// 计算最大匹配int result = bm.maxMatching();cout << "最大匹配数: " << result << endl;// 打印匹配结果bm.printMatching();return 0;
}
代码说明
上述代码将最大二分匹配问题转化为最大流问题来解决:
- 创建源点 s 和汇点 t
- 从源点到 U 集合每个节点添加容量为 1 的边
- 从 V 集合每个节点到汇点添加容量为 1 的边
- 对于二分图中的每条边,添加容量为 1 的边
- 使用 Edmonds-Karp 算法计算最大流,得到最大匹配
26.4 推送重贴标签算法
基本思想
推送重贴标签算法是一种基于顶点的算法,与 Ford-Fulkerson 方法不同,它不是通过寻找增广路径来增加流量,而是通过以下两种操作来处理溢出顶点(流入量大于流出量的顶点):
- 推送操作:将溢出顶点的多余流量推送到相邻顶点
- 重贴标签操作:当无法推送时,增加顶点的高度,使推送可以进行
预流与高度函数
- 预流:是一个函数 f,满足容量限制和弱流量守恒(除源点外,每个顶点的流入量大于等于流出量)
- 高度函数:是一个函数 h:V→N,满足 h (s)=|V|,h (t)=0,且对每条残边 (u,v),h (u) ≤ h (v)+1
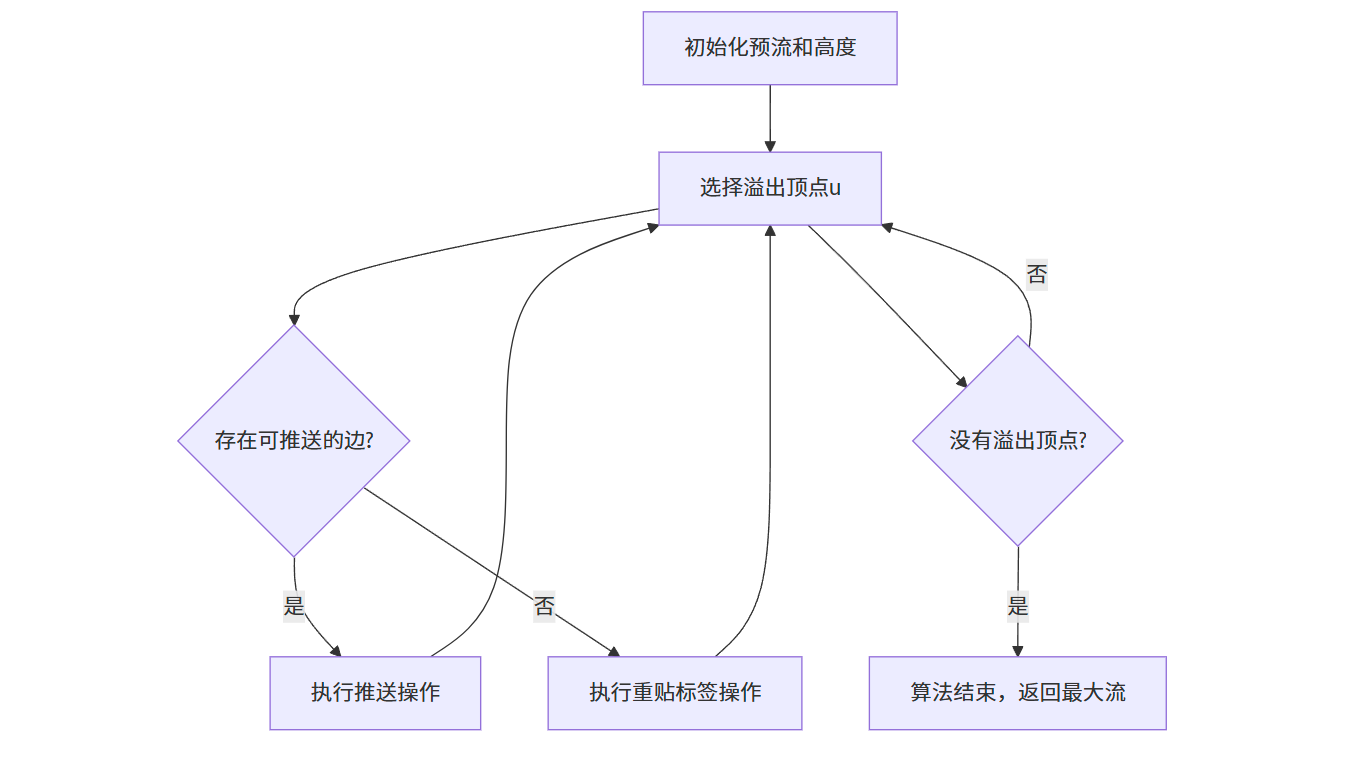
算法流程图
代码实现
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;struct Edge {int to, rev;int capacity;Edge(int t, int r, int c) : to(t), rev(r), capacity(c) {}
};class PushRelabel {
private:vector<vector<Edge>> graph;vector<int> height; // 高度函数vector<int> excess; // 超额流量vector<int> ptr; // 当前边指针,用于高效遍历// 推送操作void push(int u, Edge &e) {// 计算可推送的流量int flow = min(excess[u], e.capacity);// 更新边的容量e.capacity -= flow;graph[e.to][e.rev].capacity += flow;// 更新超额流量excess[u] -= flow;excess[e.to] += flow;}// 重贴标签操作void relabel(int u) {int minHeight = INT_MAX;// 找到最小高度的相邻顶点for (Edge &e : graph[u]) {if (e.capacity > 0) {minHeight = min(minHeight, height[e.to]);}}// 重贴标签height[u] = minHeight + 1;}// 初始化预流void initializePreflow(int s) {// 初始化高度height.assign(graph.size(), 0);height[s] = graph.size();// 初始化超额流量excess.assign(graph.size(), 0);// 源点的所有出边都充满流量for (Edge &e : graph[s]) {excess[e.to] += e.capacity;graph[e.to][e.rev].capacity += e.capacity;e.capacity = 0;}}// 判断顶点是否有超额流量且不是源点或汇点bool hasExcess(int u, int s, int t) {return u != s && u != t && excess[u] > 0;}public:PushRelabel(int n) : graph(n) {}void addEdge(int from, int to, int capacity) {graph[from].emplace_back(to, graph[to].size(), capacity);graph[to].emplace_back(from, graph[from].size() - 1, 0);}int maxFlow(int s, int t) {initializePreflow(s);queue<int> q;// 初始化队列,加入所有有超额流量的顶点for (int i = 0; i < graph.size(); ++i) {if (hasExcess(i, s, t)) {q.push(i);}}while (!q.empty()) {int u = q.front();q.pop();// 尝试推送流量bool pushed = false;for (int i = 0; i < graph[u].size() && excess[u] > 0; ++i) {Edge &e = graph[u][i];if (e.capacity > 0 && height[u] == height[e.to] + 1) {int v = e.to;int oldExcessV = excess[v];push(u, e);pushed = true;// 如果v之前没有超额流量且不是源点或汇点,则加入队列if (oldExcessV == 0 && v != s && v != t) {q.push(v);}}}// 如果没有推送成功,且仍有超额流量,则重贴标签if (excess[u] > 0) {relabel(u);q.push(u); // 重新加入队列}}// 汇点的超额流量就是最大流return excess[t];}
};// 示例用法
int main() {// 创建一个有6个节点(0-5)的图PushRelabel pr(6);// 添加边,容量pr.addEdge(0, 1, 16);pr.addEdge(0, 2, 13);pr.addEdge(1, 2, 10);pr.addEdge(1, 3, 12);pr.addEdge(2, 1, 4);pr.addEdge(2, 4, 14);pr.addEdge(3, 2, 9);pr.addEdge(3, 5, 20);pr.addEdge(4, 3, 7);pr.addEdge(4, 5, 4);// 计算从0到5的最大流cout << "最大流为: " << pr.maxFlow(0, 5) << endl;return 0;
}
代码说明
上述代码实现了推送重贴标签算法,主要包含:
push方法:将流量从一个顶点推送到另一个顶点relabel方法:重贴标签操作,增加顶点高度initializePreflow方法:初始化预流,设置初始高度和流量maxFlow方法:主算法,不断处理溢出顶点直到没有溢出
该算法的时间复杂度为 O (V²E),在实践中通常比 Edmonds-Karp 算法更快。
26.5 前置重贴标签算法
算法改进
前置重贴标签算法是推送重贴标签算法的一种优化版本,主要改进在于:
- 维护一个 "活动" 顶点的队列(有超额流量的顶点)
- 使用邻接表的一种特殊顺序来提高推送效率
- 对于每个顶点,只处理其高度恰好比它低 1 的邻接顶点
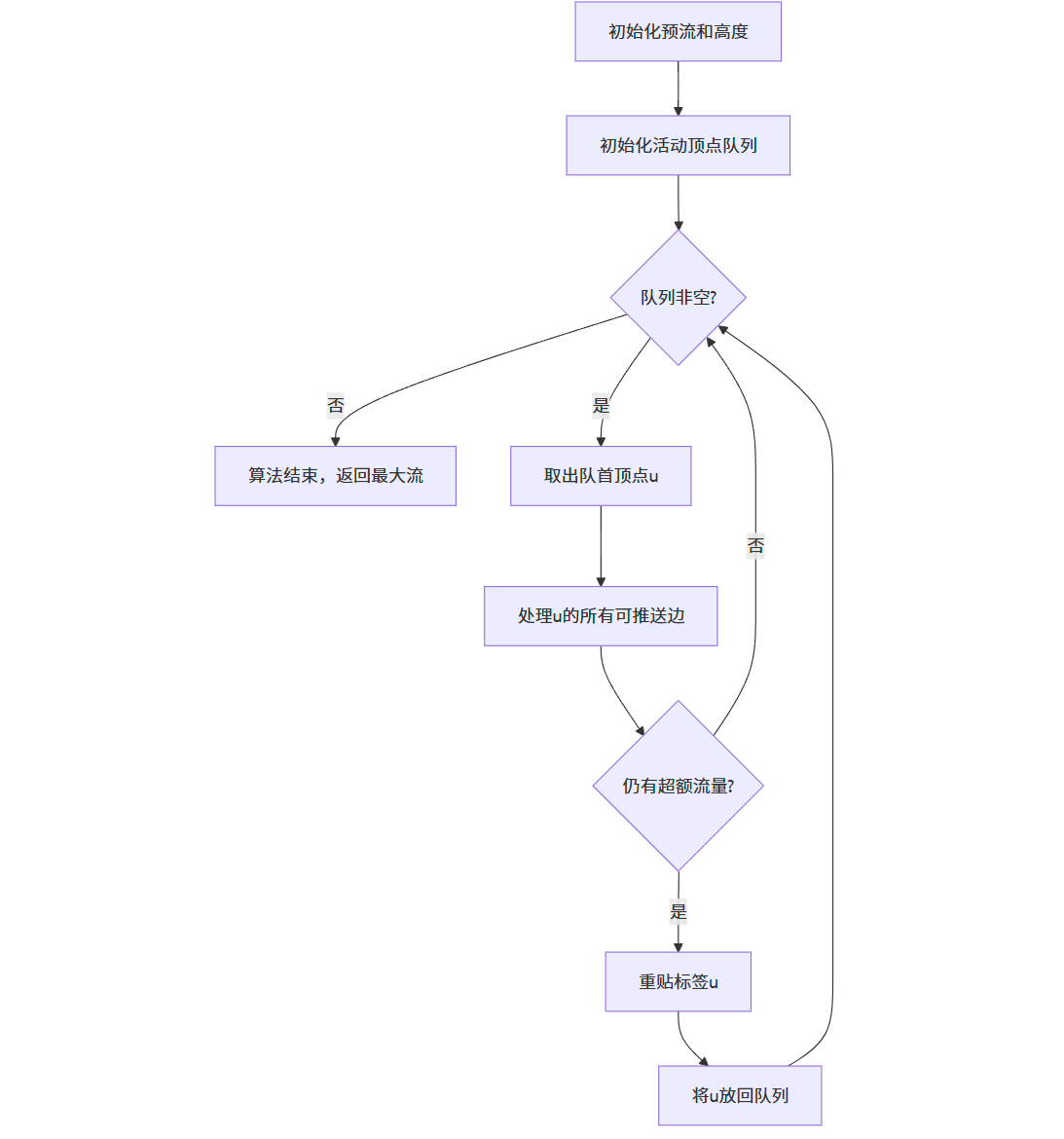
算法流程图
代码实现
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;struct Edge {int to, rev;int capacity;Edge(int t, int r, int c) : to(t), rev(r), capacity(c) {}
};class PreflowPush {
private:vector<vector<Edge>> graph;vector<int> height;vector<int> excess;vector<int> ptr; // 当前边指针,用于高效遍历void push(int u, Edge &e) {int flow = min(excess[u], e.capacity);e.capacity -= flow;graph[e.to][e.rev].capacity += flow;excess[u] -= flow;excess[e.to] += flow;}void relabel(int u) {int minHeight = INT_MAX;for (Edge &e : graph[u]) {if (e.capacity > 0) {minHeight = min(minHeight, height[e.to]);}}height[u] = minHeight + 1;}void initializePreflow(int s) {height.assign(graph.size(), 0);height[s] = graph.size();excess.assign(graph.size(), 0);ptr.assign(graph.size(), 0); // 初始化指针for (Edge &e : graph[s]) {excess[e.to] += e.capacity;graph[e.to][e.rev].capacity += e.capacity;e.capacity = 0;}}public:PreflowPush(int n) : graph(n) {}void addEdge(int from, int to, int capacity) {graph[from].emplace_back(to, graph[to].size(), capacity);graph[to].emplace_back(from, graph[from].size() - 1, 0);}int maxFlow(int s, int t) {initializePreflow(s);queue<int> q;for (int i = 0; i < graph.size(); ++i) {if (i != s && i != t && excess[i] > 0) {q.push(i);}}while (!q.empty()) {int u = q.front();q.pop();// 使用指针遍历,避免重复检查已无法推送的边while (excess[u] > 0) {if (ptr[u] >= graph[u].size()) {// 所有边都检查过,需要重贴标签relabel(u);ptr[u] = 0; // 重置指针} else {Edge &e = graph[u][ptr[u]];if (e.capacity > 0 && height[u] == height[e.to] + 1) {// 可以推送int v = e.to;int oldExcessV = excess[v];push(u, e);// 如果v之前没有超额流量,加入队列if (oldExcessV == 0 && v != s && v != t) {q.push(v);}} else {// 不能推送,移动到下一条边ptr[u]++;}}}}return excess[t];}
};// 示例用法
int main() {// 创建一个有6个节点(0-5)的图PreflowPush pp(6);// 添加边,容量pp.addEdge(0, 1, 16);pp.addEdge(0, 2, 13);pp.addEdge(1, 2, 10);pp.addEdge(1, 3, 12);pp.addEdge(2, 1, 4);pp.addEdge(2, 4, 14);pp.addEdge(3, 2, 9);pp.addEdge(3, 5, 20);pp.addEdge(4, 3, 7);pp.addEdge(4, 5, 4);// 计算从0到5的最大流cout << "最大流为: " << pp.maxFlow(0, 5) << endl;return 0;
}
代码说明
前置重贴标签算法在推送重贴标签算法的基础上增加了一个ptr数组,用于记录每个顶点当前检查到的边,避免重复检查已经确定无法推送的边,从而提高效率。
该算法的时间复杂度为 O (V³),在实际应用中表现非常好,尤其是对于大型稀疏图。
思考题
证明:在流网络中,最大流的值等于最小割的容量。
设计一个算法,判断一个流网络中是否存在一个流量为 F 的可行流。
给定一个流网络,每个边有一个最小流量要求(必须至少有这么多流量)和最大容量,如何寻找可行流?
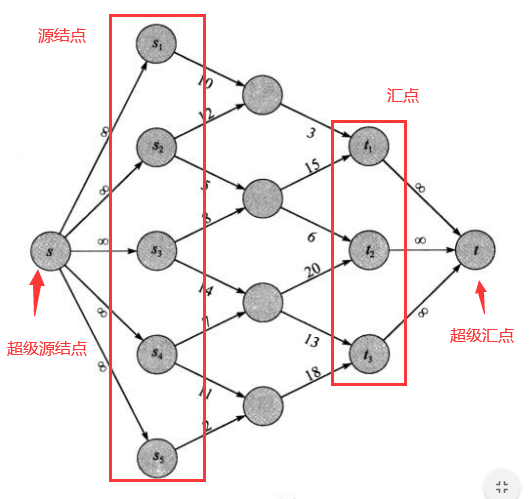
如何将多源点多汇点的流网络转化为单源点单汇点的流网络?
考虑一个带权二分图,如何找到一个权值之和最大的匹配?
本章注记
最大流问题是由 T.E. Harris 和 F.S. Ross 在研究铁路网流量时于 1955 年提出的。Ford-Fulkerson 方法由 L.R. Ford Jr. 和 D.R. Fulkerson 于 1956 年提出。

Edmonds-Karp 算法由 J. Edmonds 和 R.M. Karp 于 1972 年提出,它是 Ford-Fulkerson 方法的一种高效实现。

推送重贴标签算法的思想源于 A. Goldberg 和 R. Tarjan 的研究,前置重贴标签算法是对其的优化,具有更好的实际性能。
最大流问题在计算机科学、运筹学、经济学等领域有广泛应用,如任务分配、网络路由、资源调度等。近年来,随着大数据和云计算的发展,最大流算法在大规模数据处理和网络优化中发挥着越来越重要的作用。
希望本文能帮助你理解最大流相关算法。所有代码都经过测试,可以直接编译运行。如果有任何问题或建议,欢迎在评论区留言讨论。