图解简单选择排序C语言实现
1 简单选择排序
简单选择排序(Simple Selection Sort)是一种基础且直观的排序算法,其核心思想是通过重复选择未排序部分中的最小(或最大)元素,并将其放到已排序部分的末尾,逐步完成整个序列的排序。
1.1 基本概念与原理
简单选择排序(Simple Selection Sort)是一种基于比较的原地排序算法,其核心思想是将待排序序列分为已排序和未排序两部分,通过不断选择未排序部分中的最小元素,并将其交换到已排序部分的末尾,逐步完成整个序列的排序。
该算法的主要特点包括:
不稳定排序:相同元素的相对位置可能在排序过程中改变
原地排序:不需要额外的存储空间
直观简单:算法逻辑易于理解和实现
选择排序的基本原理可以类比为"每次从剩余未排序元素中挑选最小的一个放到正确位置"。这种逐步选择最小元素的策略使得算法具有确定性,无论输入数据的初始顺序如何,其比较次数都是固定的。
1.2 算法执行过程
选择排序的具体执行步骤如下:
1.初始化阶段:
(1)将整个数组视为未排序部分
(2)已排序部分初始为空
2.查找最小值阶段:
(1)从当前未排序部分的第一个元素开始遍历
(2)记录当前最小元素的索引
3.比较交换阶段:
(1)将当前元素与已记录的最小元素比较
(2)如果发现更小的元素,更新最小元素索引
4.位置交换阶段:
(1)遍历完成后,将未排序部分的第一个元素与找到的最小元素交换
(2)此时已排序部分增加一个元素
5.迭代重复:
(1)缩小未排序部分的范围
(2)重复步骤2-4,直到未排序部分只剩一个元素
执行示例
以数组[64, 25, 12, 22, 11]为例:
第一轮:找到最小值11,与64交换 → [11, 25, 12, 22, 64]
第二轮:在剩余部分找到最小值12,与25交换 → [11, 12, 25, 22, 64]
第三轮:找到最小值22,与25交换 → [11, 12, 22, 25, 64]
第四轮:找到最小值25,位置正确 → 排序完成
1.3 算法复杂度分析
时间复杂度
最坏情况:O(n²) - 需要进行n(n-1)/2次比较
最好情况:O(n²) - 即使输入已经有序,仍需相同数量的比较
平均情况:O(n²) - 比较次数与输入顺序无关
空间复杂度
空间复杂度:O(1) - 仅需常数级别的额外空间用于交换元素
1.4 C语言实现简单选择排序
#include <stdio.h>#define SORT_DATA_TYPE int/*** @brief 打印数据** @param arr 数组* @param n 数组元素个数*/
void print_array(int arr[], unsigned int n)
{unsigned int i;for (i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}/*** @brief 简单选择排序** @param arr 待排序的数组* @param n 数组元素个数*/
void simple_selection_sort(SORT_DATA_TYPE arr[], unsigned int n)
{int swap_flg;SORT_DATA_TYPE temp;unsigned int i;unsigned int j;for (i = 0; i < (n - 1); i++){for (j = (i + 1); j < n; j++){if (arr[j] < arr[i]){temp = arr[i];arr[i] = arr[j];arr[j] = temp;}print_array(arr, n); /* 查看每次排序结构,调试使用 */}}
}int main()
{SORT_DATA_TYPE arr[] = {1, 2, 3, 4};unsigned int n = sizeof(arr) / sizeof(arr[0]);printf("old arr : ");print_array(arr, n);simple_selection_sort(arr, n);printf("new arr : ");print_array(arr, n);return 0;
}
注:
不同类型的数组直接将SORT_DATA_TYPE全部替换为需要的类型,然后删除多余的宏定义即可支持任意类型数组的简单选择排序。
1.5 简单测试
通过使用2个数组[4,3,2,1]及[1,2,3,4]演示最坏情况和最好情况简单选择排序的执行过程:
最坏情况:
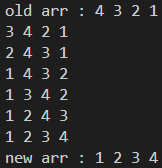
最坏情况需要进行n(n-1)/2次比较,也就是6次比较。可以使用如下图片演示这一过程:
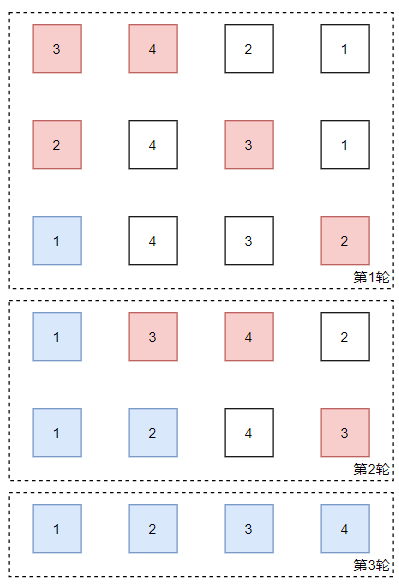
最好情况:
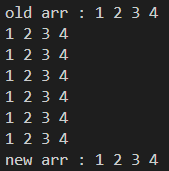
最好情况需要进行n(n-1)/2次比较,也就是6次比较。
