数据结构：二叉树的遍历 (Binary Tree Traversals)

目录

为什么需要遍历？

基本元素的定义与我们的“选择”

逐一推导遍历算法

前序遍历 (Pre-order Traversal): D -> L -> R

推导过程:

代码实现 (逐步完善):

中序遍历 (In-order Traversal): L -> D -> R

推导过程:

代码实现 (逐步完善):

后序遍历 (Post-order Traversal): L -> R -> D

---

为什么需要遍历？

我们先忘掉所有算法，回到原点思考一个问题：

我们创建了一个二叉树，把一堆数据存了进去。现在，我需要把树里所有的节点都访问一遍（比如，打印出来、或者每个节点的值都加1）。我应该怎么做才能保证不重不漏？

这就是“遍历”这个概念的本质：

设计一个确定的规则，系统性地访问树中的每一个节点，且每个节点只访问一次。

---

基本元素的定义与我们的“选择”

对于树中的任何一个节点（我们叫它 node），它都有三个关键部分需要我们处理：

1. 节点本身的数据 (我们称之为 Data，或者叫 根 R(oot))

2. 节点的整个左子树 (Left Subtree, L)

3. 节点的整个右子树 (Right Subtree, R)

既然我们的目标是处理这三个部分，那么最核心的问题就变成了：

我们应该以什么样的顺序来处理 L、D、R 这三者呢？

这是我们唯一可以做选择的地方。不同的选择顺序，就构成了不同的遍历方法。

我们来做个排列组合。L、D、R 三个元素的排列顺序有 3=6 种：

1. DLR

2. LDR

3. LRD

4. DRL

5. RDL

6. RLD

在计算机科学中，我们通常更关心“先访问左子树还是右子树”的相对顺序。

习惯上，我们总是先处理左子树，再处理右子树。这样，上面 6 种就只剩下前 3 种最常用、最经典了：

• DLR: 先处理 根节点 (D)，再处理 左子树 (L)，最后处理 右子树 (R)。

• LDR: 先处理 左子树 (L)，再处理 根节点 (D)，最后处理 右子树 (R)。

• LRD: 先处理 左子树 (L)，再处理 右子树 (R)，最后处理 根节点 (D)。

这三个顺序，就对应着三种最核心的深度优先遍历方式：前序遍历、中序遍历 和 后序遍历。

名字就是根据“根”(D) 在序列中的位置来起的。

• D在最前面 -> 前序遍历 (Pre-order Traversal)

• D在中间 -> 中序遍历 (In-order Traversal)

• D在最后面 -> 后序遍历 (Post-order Traversal)

现在，我们就来逐一推导它们的实现。

---

逐一推导遍历算法

在开始写代码之前，我们先定义好树的节点结构。这是一个你已经很熟悉的、最基础的二叉树节点：

#include <stdio.h>
#include <stdlib.h>// 二叉树节点结构定义
typedef struct Node {char data; // 为了方便演示，我们用字符类型struct Node* left;struct Node* right;
} Node;

同时，我们构建一个用于后续所有讲解的示例树。这棵树结构清晰，足以说明所有情况。

示例树:

      A/ \B   C/ \   \D   E   F

创建这棵树的代码（这个你可以先放一边，主要是为了让后面的遍历代码能跑起来）：

// 创建新节点的辅助函数
Node* createNode(char data) {Node* newNode = (Node*)malloc(sizeof(Node));newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 构建我们的示例树
Node* build_example_tree() {Node* root = createNode('A');root->left = createNode('B');root->right = createNode('C');root->left->left = createNode('D');root->left->right = createNode('E');root->right->right = createNode('F');return root;
}

好了，准备工作完成，我们开始推导！

---

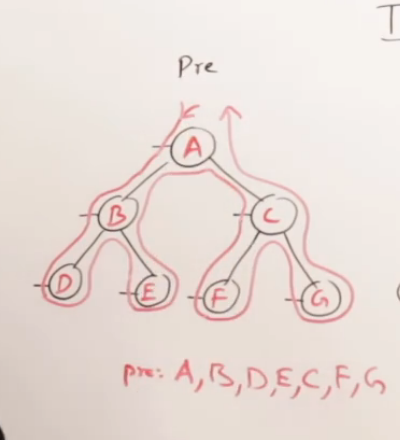
前序遍历 (Pre-order Traversal): D -> L -> R

推导过程:

我们的规则是：根 -> 左 -> 右。

这个规则不仅适用于整棵树的根节点，也同样适用于任何一个子树的根节点。这就是“递归”思想的来源。

让我们用这个规则来手动走一遍示例树：

      A/ \B   C/ \   \D   E   F

1. 从整棵树的根节点 A 开始。

2. 处理规则D (根): 访问 A。 输出: A

3. 处理规则L (左): 接下来要处理 A 的整个左子树（以 B 为根）。

• 现在我们到了 B。对 B 这个子树应用同样的 根->左->右 规则。

• 处理规则D (根): 访问 B。 输出: A B

• 处理规则L (左): 接下来处理 B 的左子树（以 D 为根）。

  • 到了 D。对 D 应用 根->左->右 规则。

  • 处理规则D (根): 访问 D。 输出: A B D

  • 处理规则L (左): D 的左子树是 NULL，什么也不做。

  • 处理规则R (右): D 的右子树是 NULL，什么也不做。

  • D 的处理全部完成。返回到 B。

• B 的左子树已经处理完了。现在轮到处理规则R (右): 处理 B 的右子树（以 E 为根）。

  • 到了 E。对 E 应用 根->左->右 规则。

  • 处理规则D (根): 访问 E。 输出: A B D E

  • 处理规则L (左): E 的左子树是 NULL。

  • 处理规则R (右): E 的右子树是 NULL。

  • E 的处理全部完成。返回到 B。

• B 的左、右子树都处理完了。 B 的处理全部完成。返回到 A。

4. A 的左子树已经处理完了。现在轮到处理规则R (右): 处理 A 的右子树（以 C 为根）。

• 到了 C。对 C 应用 根->左->右 规则。

• 处理规则D (根): 访问 C。 输出: A B D E C

• 处理规则L (左): C 的左子树是 NULL。

• 处理规则R (右): 处理 C 的右子树（以 F 为根）。

  • 到了 F。对 F 应用 根->左->右 规则。

  • 处理规则D (根): 访问 F。 输出: A B D E C F

  • ...F 的左右子树都是 NULL。

  • F 处理完成，返回到 C。

• C 处理完成，返回到 A。

5. A 的所有部分都处理完了。遍历结束。

最终输出序列: A B D E C F

代码实现 (逐步完善):

我们来把上面的逻辑翻译成代码。我们需要一个函数，比如叫 preOrder，它接收一个节点指针 root。

void preOrder(Node* root) {// 我们的第一步是思考：什么时候停下来？// 当我们遇到的节点是 NULL 时，说明这里没有树了，就应该直接返回。// 这是递归的“出口”或“基准情况”(base case)。if (root == NULL) {return;}// 如果程序能走到这里，说明 root 不是 NULL。// 接下来，我们就严格按照 D -> L -> R 的顺序写代码。// D: 访问根节点。这里我们用打印来表示“访问”。printf("%c ", root->data);// L: 遍历左子树。怎么遍历？用同样的前序遍历规则，所以我们调用自己。preOrder(root->left);// R: 遍历右子树。同样，调用自己。preOrder(root->right);
}

看，代码和我们的推导逻辑是完全一致的！三行核心代码 printf, preOrder(left), preOrder(right) 精确地对应了 D, L, R 的顺序。

---

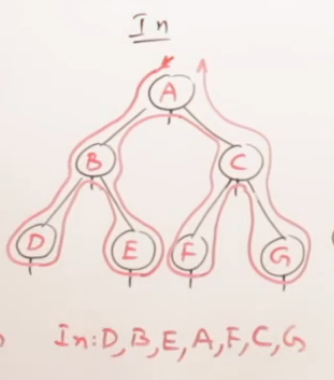
中序遍历 (In-order Traversal): L -> D -> R

推导过程:

规则变成了：左 -> 根 -> 右。我们再手动走一遍。

1. 从根节点 A 开始。

2. 处理规则L (左): 先不访问 A，而是去处理 A 的整个左子树（以 B 为根）。

      A/ \B   C/ \   \D   E   F

• 到了 B。对 B 应用 左->根->右 规则。

• 处理规则L (左): 先不访问 B，去处理 B 的左子树（以 D 为根）。

  • 到了 D。对 D 应用 左->根->右 规则。

  • 处理规则L (左): D 的左子树是 NULL。

  • 处理规则D (根): 左边没了，现在访问 D。 输出: D

  • 处理规则R (右): D 的右子树是 NULL。

  • D 处理完成，返回到 B。

• B 的左子树 (D) 处理完了。现在轮到处理规则D (根): 访问 B。 输出: D B

• 处理规则R (右): 处理 B 的右子树（以 E 为根）。

  • 到了 E。对 E 应用 左->根->右 规则。

  • 处理规则L (左): E 的左子树是 NULL。

  • 处理规则D (根): 访问 E。 输出: D B E

  • 处理规则R (右): E 的右子树是 NULL。

  • E 处理完成，返回到 B。

• B 的所有部分都处理完了。返回到 A。

3. A 的左子树 (B子树) 处理完了。现在轮到处理规则D (根): 访问 A。 输出: D B E A

4. 处理规则R (右): 处理 A 的右子树（以 C 为根）。

• 到了 C。对 C 应用 左->根->右 规则。

• 处理规则L (左): C 的左子树是 NULL。

• 处理规则D (根): 访问 C。 输出: D B E A C

• 处理规则R (右): 处理 C 的右子树（以 F 为根）。

  • 到了 F。对 F 应用 左->根->右 规则。

  • ...先左(NULL)，再访问 F，再右(NULL)。 输出: D B E A C F

  • F 处理完成，返回 C。

• C 处理完成，返回 A。

5. A 的所有部分都处理完了。遍历结束。

最终输出序列: D B E A C F

代码实现 (逐步完善):

这次我们只需要调整一下 D, L, R 的代码顺序，就能得到中序遍历的函数。

void inOrder(Node* root) {// 递归的出口，和前序遍历完全一样。if (root == NULL) {return;}// 严格按照 L -> D -> R 的顺序写代码。// L: 遍历左子树。inOrder(root->left);// D: 访问根节点。printf("%c ", root->data);// R: 遍历右子树。inOrder(root->right);
}

发现了吗？我们仅仅是把 printf 语句从第一行移动到了第二行，就实现了完全不同的遍历逻辑。这就是第一性原理的威力——理解了 L, D, R 的排列，就理解了所有这些遍历方法。

---

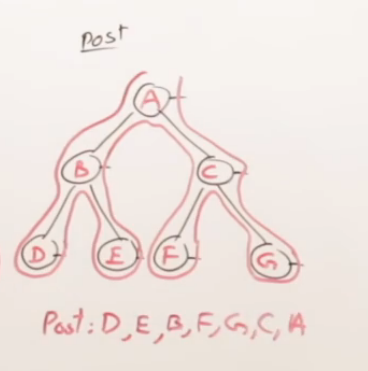
后序遍历 (Post-order Traversal): L -> R -> D

推导过程:

规则是：左 -> 右 -> 根。

这次你可能可以自己尝试在纸上推导一下了。它的特点是，一个根节点必须等到它的左右孩子都访问完毕后，才能被访问。

手动推导结果： D -> E -> B -> F -> C -> A

代码实现 (逐步完善):

同样，我们只是调整代码顺序。

void postOrder(Node* root) {// 递归出口不变if (root == NULL) {return;}// 严格按照 L -> R -> D 的顺序写代码。// L: 遍历左子树postOrder(root->left);// R: 遍历右子树postOrder(root->right);// D: 访问根节点printf("%c ", root->data);
}

后序遍历在某些场景下非常有用，比如释放树的内存。因为你必须先释放子节点的内存，才能安全地释放父节点的内存，这和后序遍历的顺序完全一致。

---

未完待续……