数学分析| 极限论| 1.数列极限常用方法总结

极限是数学分析的基础，也是后续所有学习的根基，微分、积分、级数无不例外都需要扎实的极限作为基础，因此在学习过程中，务必要弄清搞懂不同类型的极限在求解过程中应该使用怎样的方法才能快速的进行题目的分析与求解。本文将以极限论作为引子开启数学分析强化学习的旅程，今天将大致介绍在数列极限中常用的求解方法，后面的推文将会以专题形式对其中的某几种办法进行详细介绍。

---

常用求解数列极限的办法

1.定义法

       直接使用数列极限的定义进行证明，但是该方法需要预先能够猜到数列的极限值。

2.极限的四则运算

       如果原数列的通项可以被拆成简单项组合的形式进行四则运算，前提是每一个简单项应该也具有极限。

3.迫敛性定理

       对于较复杂的数列通项，可以用两个极限相同的简单数列将此复杂数列夹在中间，将复杂的问题转化为求解两个简单的数列通项极限。

4.数列与子列的关系

       有关数列与子列的两条结论应该熟记：①数列收敛的充要条件为其任何一个非平凡子列收敛。②单调数列，若有一子列收敛，则数列收敛。

5.单调有界定理

       顾名思义，对于一个数列而言，从两个维度进行分析，如果能证明其单调【单调递增、单调递减均无所谓】且有界，则能进一步证明出该数列的极限存在。此时，单调递增且有上界的数列的极限值为其上确界；单调递减且有下界的数列的极限值为其下确界。

6.柯西收敛准则

       柯西收敛准则在使用过程中，充分考察对于分析性语言的考察，一定要注意使用的条件是否合理。

7.海涅定理(归结原则)

       该定理可以视为数列极限与函数极限的“桥梁”，利用海涅定理后，可以接连使用洛必达法则处理函数极限，进而分析“离散型”的数列极限。

8.常用的数列极限类型

       注意对常见数列极限的熟悉与掌握，做题时有时可以直接套用。

9.初等变形

       有些时候，对于原数列进行适当变形有助于进一步求解，比如分母有理化、裂项相消等技巧的运用。

10.递推法

       该类型数列比较容易识别，常为递推数列与压缩数列，这些数列在证明过程中常与单调有界定理相结合进行使用。

11.平均收敛定理

       算术平均收敛与几何平均收敛两个定理极其重要，必须牢固掌握。

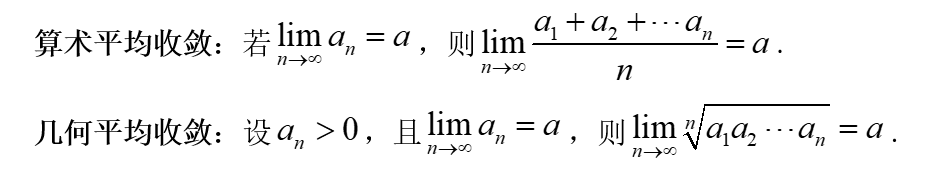
12.Stolz定理

       Stolz定理也是十分重要的转化公式，对于一些连加型数列，往往常常使用该定理求解。

13.利用上下极限

14.Taylor公式

       Taylor公式的重要性不言而喻，对于同阶比式运算极其好用。

15.积分法

        对于某些特定的数列可以视为积分进行计算，在计算过程中，最重要的是寻找被积函数、积分上下限，进而便转化为积分的计算。

16.级数法

        结合级数收敛的必要条件，可以快速判定数列极限为0。

17.Fourier级数

       对于某个函数进行Fourier展开，在某个点处的值便是数列的形式，因此可以进行数列极限的求解。

---

上面所介绍的各种方法便是在数列极限计算过程中常用的方法，后面的文章将会借助对应的题目对其中的某几种方法进行专项讲解。