当前位置：首页 > news >正文

深度学习-卷积神经网络CNN-膨胀卷积、可分离卷积（空间可分离、深度可分离）、分组卷积

news 2025/8/15 14:51:38

卷积

1. 膨胀卷积

2. 可分离卷积

2.1 空间可分离卷积

2.2 深度可分离卷积

3. 分组卷积

卷积

1. 膨胀卷积

膨胀卷积也被称为空洞卷积或扩张卷积，是一种通过卷积核的元素之间插入“空洞”来扩展感受野的卷积操作。

膨胀卷积用膨胀率L表示u哦啊扩大内核的范围，即在内核元素间插入L-1个空格个，默认L=1时，内核元素间没有插入空格，即标准卷积

L=2时：

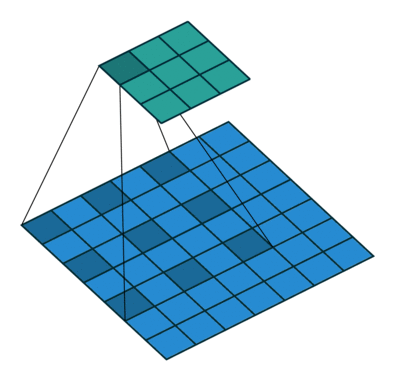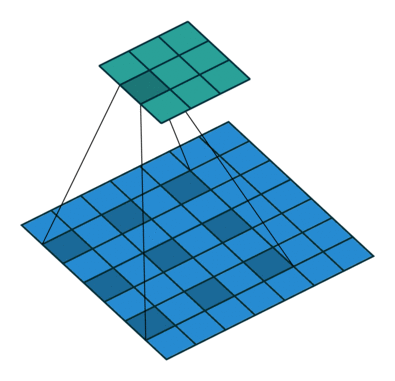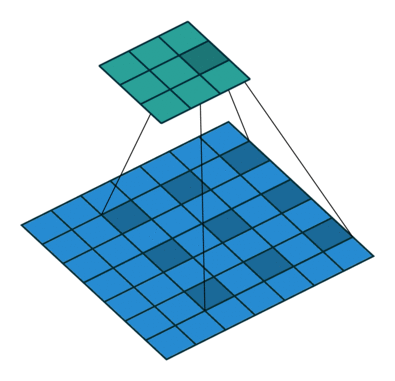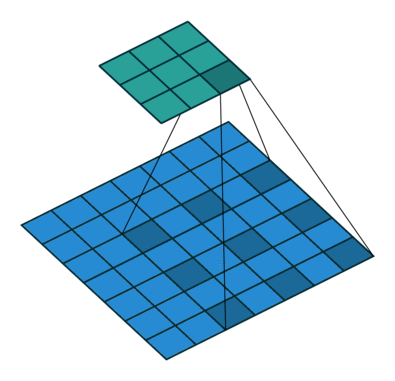
感受野（Receptive Field）：

感受野是输出特征图上某个点对应输入图像的区域大小。
膨胀卷积通过增大膨胀率 L，可以显著扩大感受野，而无需增加卷积核尺寸或步长。

标准卷积（L=1, K=3）的感受野为 3×3。
膨胀卷积（L=2, K=3）的感受野为 5×5（相当于 7×7 的覆盖范围，但只有 9 个参数）。

import torch
import torch.nn as nn

def test01():conv = nn.Conv2d(in_channels=3,out_channels=128,kernel_size=3,stride=1,dilation=2,padding=1,bias=True)out = conv(torch.randn(1,3,224,224))print(out.shape)

if __name__ == '__main__':test01()

2. 可分离卷积

可分离卷积是一种将常规卷积操作进行拆分，以减少计算量和参数量的卷积方式，主要有空间可分离卷积和深度可分离卷积两种类型。

2.1 空间可分离卷积

概念

空间可分离卷积是一种将传统二维卷积分解为两个一维卷积的操作。通过分别对图像的行和列进行卷积，减少计算量和参数量。

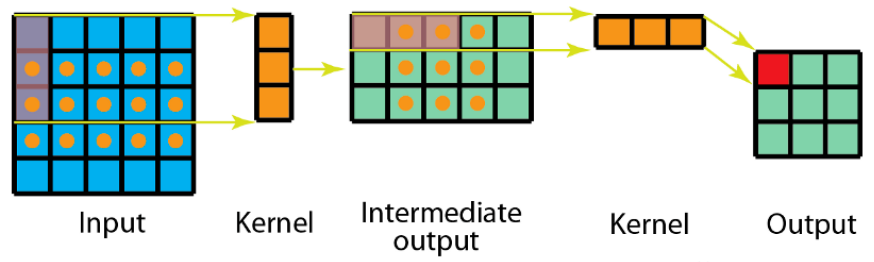
原理

标准卷积：直接使用 $k \times k$ 的二维卷积核。
空间可分离卷积：
1. 先对图像的每一行进行 $k \times 1$ 的一维卷积（水平方向）。
2. 再对结果的每一列进行 $1 \times k$ 的一维卷积（垂直方向）。
在数学中我们可以将矩阵分解：

$\left[ \begin{matrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{matrix} \right]= \left[ \begin{matrix} 1 \\ 2 \\ 1 \end{matrix} \right]\times \left[ \begin{matrix} -1 & 0 & 1 \end{matrix} \right]$
计算量对比：
- 标准卷积： $k^2 \cdot C_{in} \cdot C_{out}$
- 空间可分离卷积： $2 \cdot k \cdot C_{in} \cdot C_{out}$ 。
- 比例：当 k > 2 时，空间可分离卷积的计算量显著降低。

优点：
- 显著减少计算量
- 适用于特定可分解的卷积核（如 Sobel 核）。
缺点：
- 仅适用于可分解的卷积核，通用性差。
- 可能丢失图像的空间相关性。

实现

import torch
import torch.nn as nn

def test02():inpupt_map = torch.randn(1, 1, 7, 7)conv1 = nn.Conv2d(in_channels=1,out_channels=1,kernel_size=(3,1),stride=1,)conv2 = nn.Conv2d(in_channels=1,out_channels=1,kernel_size=(1,3),stride=1,)out = conv1(inpupt_map)out = conv2(out)print(out.shape)

if __name__ == '__main__':test02()

2.2 深度可分离卷积

深度可分离卷积是一种高效的卷积操作，通过将标准卷积分解为两个独立步骤，在保持特征提取能力的同时大幅减少计算量和参数量

深度可分离卷积将标准卷积分解为两个步骤：

深度卷积（Depthwise Convolution）：对每个输入通道独立进行卷积。
逐点卷积（Pointwise Convolution）：使用 $1 \times 1$ 卷积核融合通道信息。

原理

深度卷积：
- 输入通道 $C_{in}$ ，输出通道 $C_{in}$ （单通道处理）。
- 每个通道使用独立的卷积核。
逐点卷积：
- 使用 $1 \times 1$ 卷积核，将 $C_{in}$ 通道的信息整合为 $C_{out}$ 通道。
计算量对比：
- 标准卷积： $H' \cdot W' \cdot k^2 \cdot C_{in} \cdot C_{out}$
- 深度可分离卷积： $H' \cdot W' \cdot k^2 \cdot C_{in} + H' \cdot W' \cdot C_{in} \cdot C_{out}$
- 比例：计算量约为标准卷积的 $1/C_{out} + 1/k^2$ 。

图1：输入图的每一个通道，我们都使用了对应的卷积核进行卷积。通道数量 = 卷积核个数，每个卷积核只有一个通道

图2：完成卷积后，对输出内容进行1x1的卷积

import torch
import torch.nn as nn

def test02():input_map = torch.randn(1, 8, 7, 7)# 8*1*3*3conv1 = nn.Conv2d(in_channels=8,out_channels=8,kernel_size=3,stride=1,groups=8)# 8*8*1*1con2 = nn.Conv2d(in_channels=8,out_channels=8,kernel_size=1,stride=1,)out = conv1(input_map)out = con2(out)print(out.shape)

if __name__ == '__main__':test02()

3. 分组卷积

概念分组卷积通过将输入通道分成多个组，每组独立进行卷积操作，最后合并结果。常见于 ResNext、SqueezeNet 等模型。

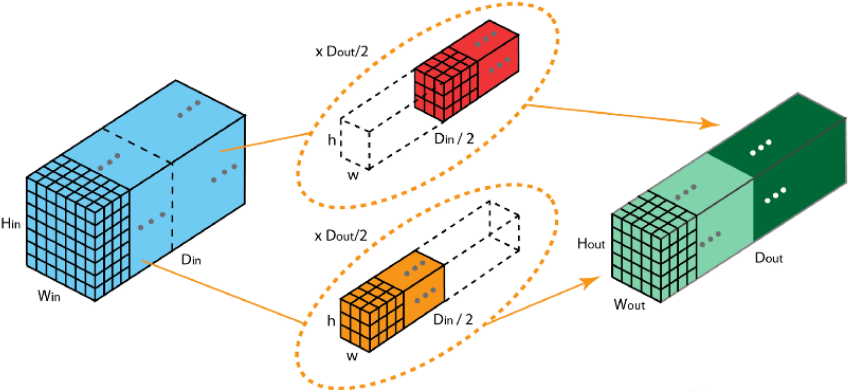
原理

分组策略：
- 输入通道 $C_{in}$ 被均分为 G 组。
- 为每个组分配独立的卷积核（每组卷积核仅处理对应组的输入通道）
- 每组卷积运算独立进行，最后将各组输出拼接得到最终结果
参数量对比：
- 标准卷积： $k^2 \cdot C_{in} \cdot C_{out}$ 。
- 分组卷积： $k^2 \cdot (C_{in}/G) \cdot C_{out}$ 。
计算量对比：
- 标准卷积： $H' \cdot W' \cdot k^2 \cdot C_{in} \cdot C_{out}$ 。
- 分组卷积： $H' \cdot W' \cdot k^2 \cdot (C_{in}/G) \cdot C_{out}$ 。

实现

import torch
import torch.nn as nn

def test01():input_map = torch.randn(1, 128,14,14)# 64*16*3*3conv = nn.Conv2d(in_channels=128,out_channels=64,kernel_size=3,stride=1,groups=8)out = conv(input_map)print(out.shape)for name,param in conv.named_parameters():print(name,param.shape)

if __name__ == '__main__':test01()

特点