2022_ISG_CTF-rechall详解（含思考过程）

一、题目来源

在看雪平台中的Reverse板块可以找到该题目

二、信息搜集

将题目给的二进制文件丢入DIE中查看是否存在加壳的现象，顺便查看文件类型

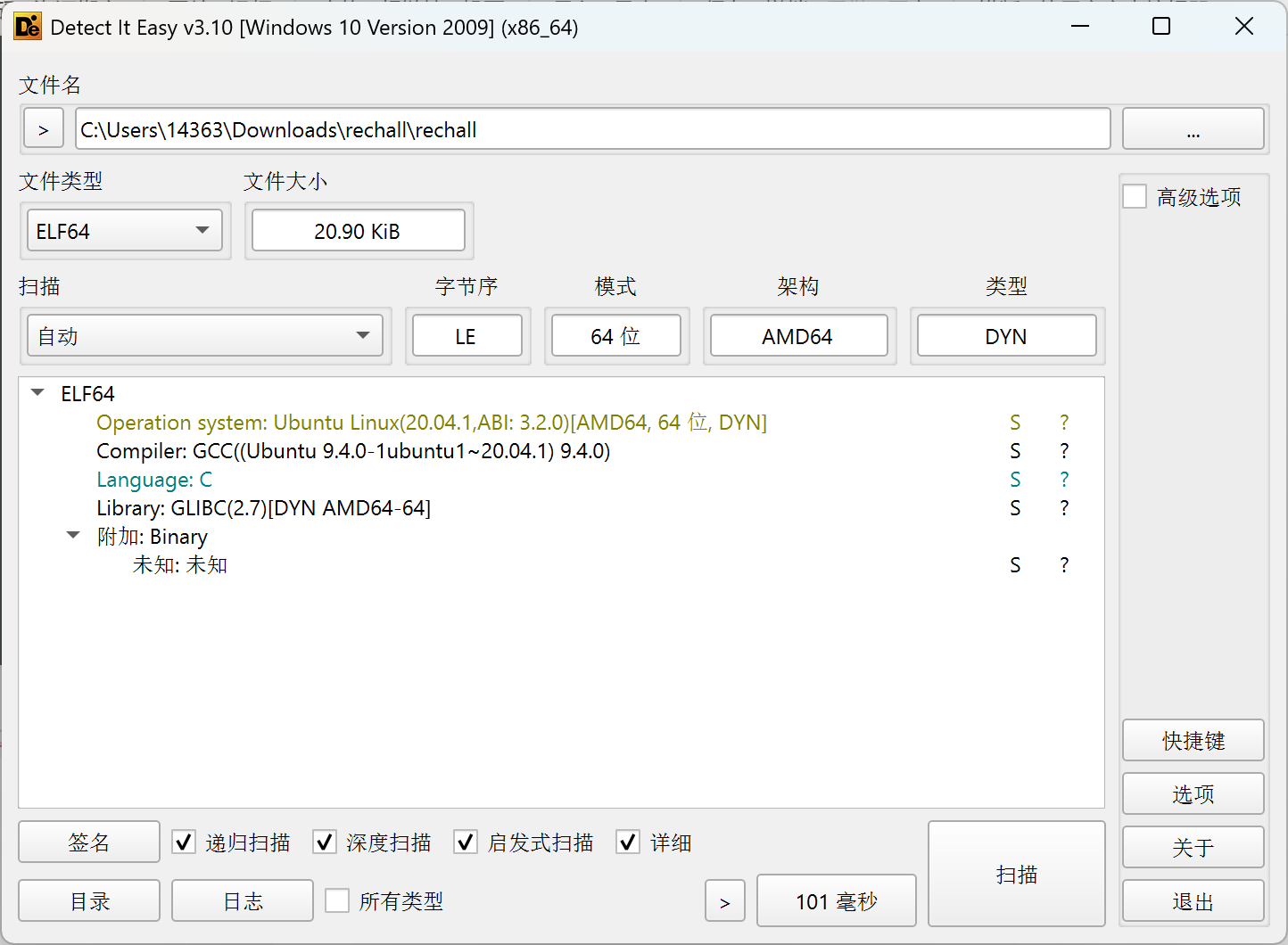
没有发现加壳的现象，而且我们知道了该文件的文件类型是64位的ELF

三、反汇编文件开始分析

将题目给的二进制文件丢入64位的IDA Pro当中，开始反汇编操作

因为Reverse类型的题目注重逻辑，我们直接通过ctrl+f5，将反汇编出来汇编代码反编译成C语言，通过C语言来分析代码逻辑

首先看到main函数：

int __cdecl main(int argc, const char **argv, const char **envp)
{__int64 v3; // rbpsigned __int64 *v4; // rsi__int64 v5; // rdx__int64 v6; // rdx__int64 v7; // rdx__int64 v8; // raxconst char *v9; // rdi__int64 v10; // rdxint result; // eaxunsigned __int64 v12; // rcxunsigned __int64 v13; // rt1unsigned int v14; // [rsp-118h] [rbp-118h]unsigned int v15; // [rsp-114h] [rbp-114h]unsigned int v16; // [rsp-110h] [rbp-110h]unsigned int v17; // [rsp-10Ch] [rbp-10Ch]__int64 v18; // [rsp-108h] [rbp-108h]signed __int64 v19; // [rsp-A8h] [rbp-A8h]signed __int64 v20; // [rsp-A0h] [rbp-A0h]__int64 v21; // [rsp-98h] [rbp-98h]__int64 v22; // [rsp-78h] [rbp-78h]unsigned __int64 v23; // [rsp-10h] [rbp-10h]__int64 v24; // [rsp-8h] [rbp-8h]__asm { endbr64 }v24 = v3;v23 = __readfsqword(0x28u);v14 = 0;sub_1120(&unk_3004, &v14, envp);v4 = (signed __int64 *)1385478001;if ( (unsigned int)checker1(v14, 1385478001LL) )goto LABEL_12;v15 = 0;v4 = (signed __int64 *)&v15;sub_1120(&unk_3004, &v15, v5);if ( (unsigned int)checker2(v15) )goto LABEL_12;v16 = 0;v4 = (signed __int64 *)&v16;sub_1120(&unk_3004, &v16, v6);if ( (unsigned int)checker3(v16) )goto LABEL_12;v17 = 0;v4 = (signed __int64 *)&v17;sub_1120(&unk_3004, &v17, v7);if ( (unsigned int)checker4(v17) )goto LABEL_12;sub_1100(&v21, 0LL, 32LL);sub_1130(&v22, "flag{%08x-%08x-%08x-%08x}", v14, v15, v16, v17);md5_init(&v18);v8 = sub_10D0(&v22);md5_update(&v18, &v22, v8);md5_final(&v18, &v21);v19 = -3548426532530039310LL;v20 = -3296693883362762886LL;v4 = &v19;if ( (unsigned int)sub_1110(&v21, &v19, 16LL) ){
LABEL_12:v9 = "Wrong!";sub_10C0("Wrong!");result = 0;}else{sub_10C0("Right!");v4 = &v22;v9 = "Your flag is: %s\n";sub_10F0("Your flag is: %s\n", &v22);result = 0;}v13 = __readfsqword(0x28u);v12 = v13 ^ v23;if ( v13 != v23 )result = sub_10E0(v9, v4, v10, v12);return result;
}

一眼就可以看到flag的样式

但是本题恶心的点就在于，有着非常多的未命名函数，比如： sub_1120

这就需要我们去分析汇编代码，然后分析出该未命名函数的原型大致是谁，然后通过重命名的方式来方便我们分析

首先看到：

  v14 = 0;sub_1120(&unk_3004, &v14, envp);v4 = (signed __int64 *)1385478001;if ( (unsigned int)checker1(v14, 1385478001LL) )goto LABEL_12;

其对应的汇编代码就是：

mov     dword ptr [rbp-110h], 0
lea     rax, [rbp-110h]
mov     rsi, rax
lea     rdi, unk_3004
mov     eax, 0
call    sub_1120
mov     eax, [rbp-110h]
mov     esi, 5294B771h
mov     edi, eax
call    checker1
test    eax, eax
jnz     loc_1650

unk_3004是sub_1120的第一个参数

点入unk_3004，就可以看到其内容：

.rodata:0000000000003004 unk_3004        db  25h ; %             ; DATA XREF: main+32↑o
.rodata:0000000000003004                                         ; main+71↑o ...
.rodata:0000000000003005                 db  75h ; u

第二个参数是rax中的值，根据汇编代码：

lea     rax, [rbp-110h]

我们知道，rax中存放的是一个地址信息（rbp-110h）

一个格式化字符，一个地址信息，这个函数就很可能就是scanf()，即使不是，也很可能是相同的逻辑，因此我们将其重命名为“my_scanf()”

IDA Pro中重命名函数的方法是：
光标移动到该函数上，然后按“n”即可重命名

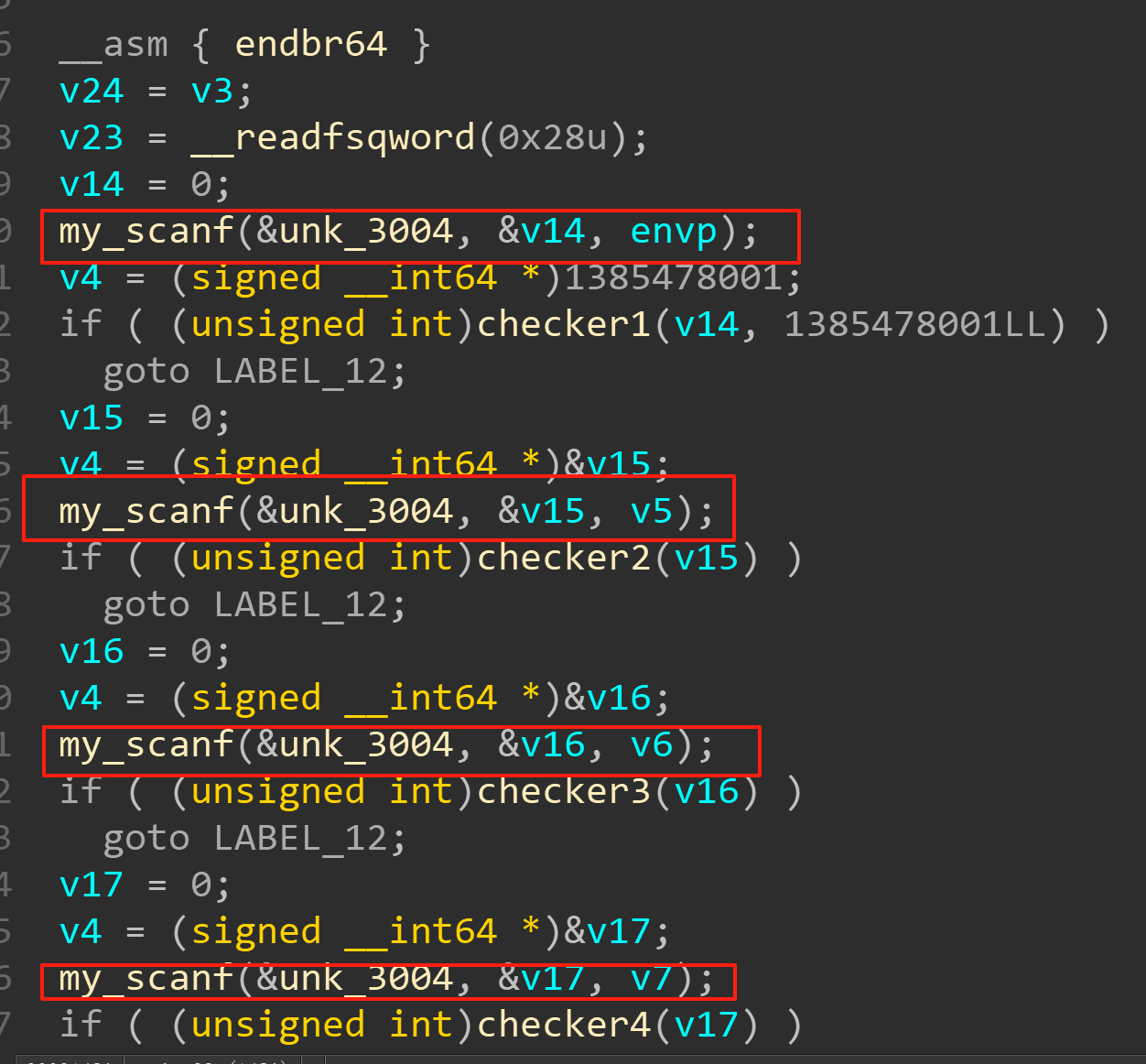
接下，我们继续分析checker1()

其对应的汇编代码就是：

mov     eax, [rbp-110h]
mov     esi, 5294B771h
mov     edi, eax
call    checker1

很明显，我们之前的输入（通过my_scanf()），会作为该函数的第一个参数

我们直接点入该函数查看函数逻辑

signed __int64 __fastcall checker1(int a1, int a2)
{signed __int64 result; // rax__int64 v3; // [rsp-8h] [rbp-8h]__asm { endbr64 }*((_DWORD *)&v3 - 5) = a1;*((_DWORD *)&v3 - 6) = a2;*((_DWORD *)&v3 - 1) = *((_DWORD *)&v3 - 5) - *((_DWORD *)&v3 - 6);if ( *((_DWORD *)&v3 - 1) == -1788593991 )result = 0LL;elseresult = 0xFFFFFFFFLL;return result;
}

这里面会对两参数进行一系列的操作，然后会有两种不同的返回值

• 0
• 其他

若返回非0值的话，那么if判断就会符合，根据代码逻辑就会跳转到：

goto LABEL_12;LABEL_12:v9 = "Wrong!";sub_10C0("Wrong!");result = 0;

直接输出“Wrong”，刚好是输出flag的对立面

换言之，我们需要通过控制输入信息，来实现checker1函数返回0

注意，my_scanf函数的格式化字符串是%u，即输入的信息会被转化成十进制的无符号数，但是在checker函数中，我们输入的信息又会被转换成int类型（有符号数）
那么，只要我们输入的是一个有符号的十进制数，这一套操作下来就相当于没操作
因此，可以直接理解为，我们输入的信息直接作为checker1的参数存在

现在我们细看里面的代码逻辑

其实就是对该函数的俩个参数进行运算，然后将最后运算的结果与-1788593991进行比较，若相等则可返回0

那么，我们就需要解方程，来得到我们需要输入的数字是什么

当然，这个函数里面还比较简单，我们可以直接通过方程的思想解出答案

但是，如果运算式非常复杂（没错，先打个预防针，后面的几个函数就是很复杂T-T），甚至有些运算没有逆操作，这样的方式就显得非常麻烦了

因此，我们直接引入一个高效的解法，就是SMT求解器

什么是SMT求解器？

SMT的全称是Satisfiability Modulo Theories（可满足性模理论）

你可以把它理解为一个超级强大的数学和逻辑方程求解器

你不需要告诉它怎么算，你只需要告诉它问题是什么（把等式和条件描述给它）

然后，它会利用高效的内部算法，尝试从逻辑上推导出一个满足你所有条件的解

其中最著名、最强大的一个就是微软研究院开发的Z3求解器，并且它有非常方便的Python接口

我们直接可以通过pip命令安装Z3的Python库

pip3 install z3-solver

构造对应的脚本：

from z3 import *def solve_with_z3():# 1. 定义一个32位的“符号变量”# 这不是一个具体的数字，而是一个代表未知数的符号，名叫'a1'a1 = BitVec('a1', 32)# 2. 目标target = -1788593991# 3. 创建一个求解器实例solver = Solver()# 4. 将C代码中的等式原封不动地翻译成Z3的约束# Z3的符号变量重载了所有的运算操作符 (&, |, ~, +, -, *)calculated_value = a1 - 1385478001# 5. 添加约束条件：告诉Z3我们希望计算结果等于目标值solver.add(calculated_value == target)# 6. 让Z3开始求解print("[*] 正在求解约束...")if solver.check() == sat:# 如果Z3说 'sat' (satisfiable)，意味着找到了解model = solver.model()solution = model[a1].as_signed_long() # 以有符号长整型获取结果print(f"[+] Z3 找到了解!")print(f"当 a1 = {solution} (十六进制: {hex(model[a1].as_long())}) 时，条件满足。")return solutionelse:# 如果是'unsat'(unsatisfiable)，意味着无解print("[-] Z3 证明此约束无解。")return None# 运行求解器
solve_with_z3()

运行结果：

我知道，用Z3求解器来解决checker1有点小题大作，但是当你看到后面的函数的时候，就会发现它的魅力的

继续看checker2

signed __int64 __fastcall checker2(int a1)
{signed __int64 result; // rax__int64 v2; // [rsp-8h] [rbp-8h]__asm { endbr64 }*((_DWORD *)&v2 - 5) = a1;*((_DWORD *)&v2 - 1) = ~(3 * (*((_DWORD *)&v2 - 5) & 0x52E3F96B)- (*((_DWORD *)&v2 - 5) | 0xAD1C0694)- *((_DWORD *)&v2 - 5)+ 1513622824);if ( *((_DWORD *)&v2 - 1) == -1035960598 )result = 0LL;elseresult = 0xFFFFFFFFLL;return result;
}

其实做的事情和checker1没什么两样（知识运算表达式的区别），都是对参数进行一系列的运算，然后比较结果是否等于一个数

我们可以看到，这里的表达式就复杂多了，而且&逻辑是没有其逆过程的

如果我们尝试枚举的方式来解决的话，最坏的情况就需要跑42亿的数据，是非常耗时的

因此，Z3解释器就变成了这里的最优解

Poc：

from z3 import *def solve_with_z3():a1 = BitVec('a1', 32)#为了后续算式更简洁，这里添加几个常量C1 = 0x52E3F96BC2 = 0xAD1C0694C3 = 1513622824target = -1035960598solver = Solver()calculated_value = ~(3 * (a1 & C1) - (a1 | C2) - a1 + C3)solver.add(calculated_value == target)print("[*] 正在求解约束...")if solver.check() == sat:model = solver.model()solution = model[a1].as_signed_long()print(f"[+] Z3 找到了解!")print(f"    当 a1 = {solution} (十六进制: {hex(model[a1].as_long())}) 时
，条件满足。")return solutionelse:print("[-] Z3 证明此约束无解。")return None# 运行求解器
solve_with_z3()

运行结果：

后面的checker3、checker4都是一样的逻辑，POC我相信大家都可以自己构造出来

唯一需要提的一点是：后续两个函数都新增了一个条件，就是对我们输入的内容有了大小的判断

拿checker3举例子

signed __int64 __fastcall checker3(int a1)
{signed __int64 result; // rax__int64 v2; // [rsp-8h] [rbp-8h]__asm { endbr64 }*((_DWORD *)&v2 - 5) = a1;if ( *((_DWORD *)&v2 - 5) > 0x10000000u )return 0xFFFFFFFFLL;*((_DWORD *)&v2 - 1) = -3 * (~*((_DWORD *)&v2 - 5) | 0xD68E3FE9)+ 3 * ~(*((_DWORD *)&v2 - 5) | 0xD68E3FE9)+ 4 * ((~*((_DWORD *)&v2 - 5) & 0xD68E3FE9) + 2 * ~(~*((_DWORD *)&v2 - 5) | 0xD68E3FE9))+ 10 * (*((_DWORD *)&v2 - 5) & 0xD68E3FE9)- (*((_DWORD *)&v2 - 5) ^ 0xD68E3FE9);if ( *((_DWORD *)&v2 - 1) == 622576829 )result = 0LL;elseresult = 0xFFFFFFFFLL;return result;
}

可以看到它多了一个if判断：

  if ( *((_DWORD *)&v2 - 5) > 0x10000000u )return 0xFFFFFFFFLL;

这个在脚本中的体现就是：

    # ULE = Unsigned Less or Equal，用于模拟C语言的无符号比较solver.add(ULE(a1, 0x10000000))

为什么是无符号的比较呢?

注意细节“0x10000000u”的后面是带有一个u（unsigned）的，即表示此次比较是无符号数之间的比较，为了完整地模拟此次比较，就需要用到ULE

那么完整的Poc3：

from z3 import *def solve_with_z3():a1 = BitVec('a1', 32)target = 622576829solver = Solver()calculated_value = -3 * (~a1 | 0xD68E3FE9) + 3 * ~(a1 | 0xD68E3FE9) + 4 * ((~a1 & 0xD68E3FE9) + 2 * ~(~a1 | 0xD68E3FE9)) + 10 * (a1 & 0xD68E3FE9) - (a1 ^ 0xD68E3FE9);#关键添加位置solver.add(ULE(a1,0x10000000))solver.add(calculated_value == target)print("[*] 正在求解约束...")if solver.check() == sat:model = solver.model()solution = model[a1].as_signed_long() print(f"[+] Z3 找到了解!")print(f"    当 a1 = {solution} (十六进制: {hex(model[a1].as_long())}) 时，条件满足。")return solutionelse:print("[-] Z3 证明此约束无解。")return Nonesolve_with_z3()

Poc4同理：

from z3 import *def solve_with_z3():a1 = BitVec('a1', 32)target = -2006746152solver = Solver()calculated_value = (11 * (a1 ^ 0xAE7C284F))\+ (4 * (a1 & 0xAE7C284F))\- (6 * (a1 & 0x5183D7B0) + 12 * ~(a1 | 0x5183D7B0))\+ (-5 * a1)\- (2 * ~(a1 | 0x4EDA6B7C))\- (a1 | 0xB1259483)\+ (3 * (a1 & 0x4EDA6B7C))\+ (4 * (a1 & 0xB1259483))\- (-2 * (a1 | 0xB1259483))\- 1367594930solver.add(ULE(a1,0x10000000))solver.add(calculated_value == target)# 6. 让 Z3 开始求解print("[*] 正在求解约束...")if solver.check() == sat:model = solver.model()solution = model[a1].as_signed_long()print(f"[+] Z3 找到了解!")print(f"    当 a1 = {solution} (十六进制: {hex(model[a1].as_long())}) 时，条件满足。")return solutionelse:print("[-] Z3 证明此约束无解。")return None# 运行求解器
solve_with_z3()

四、获得Flag

我们计算出了四次正确的输入是什么：

• 第一次：-403115990
• 第二次：-1868331135
• 第三次：88939547
• 第四次：232752086

由此，我们可以先运行程序，输入他们看看结果

我直接用脚本替代手动输入(没看懂的小伙伴可以直接手动输入四个值，效果一致)：

from pwn import *
'''-403115990
-1868331135
88939547
232752086'''
p = process("./reverse")
p.sendline(b'-403115990')
p.sendline(b'-1868331135')
p.sendline(b'88939547')
p.sendline(b'232752086')
p.interactive()

结果：

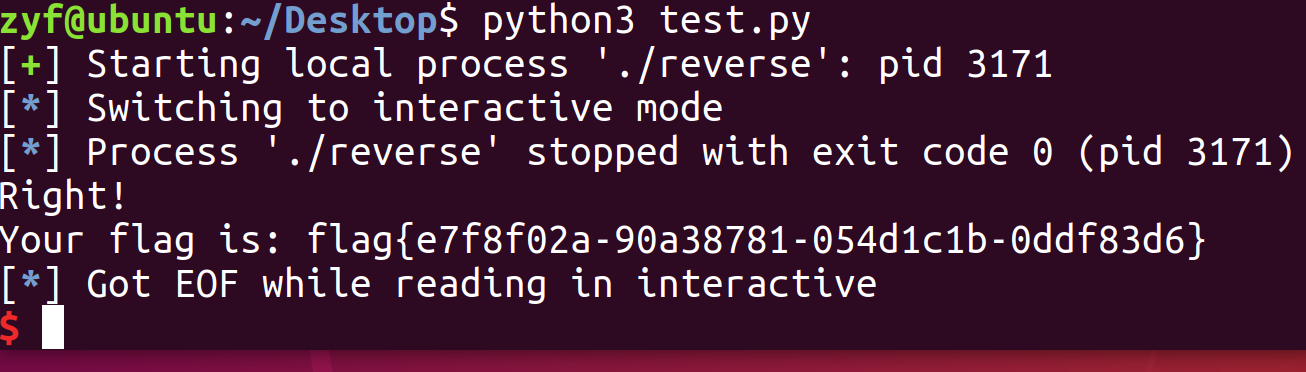
直接输出了flag，并告诉我们正确（Right！）

我们也可以根据代码逻辑手动计算

sub_1130(&v22, "flag{%08x-%08x-%08x-%08x}", v14, v15, v16, v17);

这段代码，大家看过汇编就会知道，这其实就是sprintf的逻辑

最后的flag，其实就是我们四次输入的然后转换成八位十六进制的组合

写c脚本：

#include <stdio.h>int main(){int a = -403115990;int b = -1868331135;int c = 88939547;int d = 232752086;printf("flag{%08x-%08x-%08x-%08x}",a,b,c,d);
}

编译运行后得到flag的正确结果：

与之前程序自动跑出来的结果是一致的

至此，本题结束~