笔试——Day38

第一题

题目

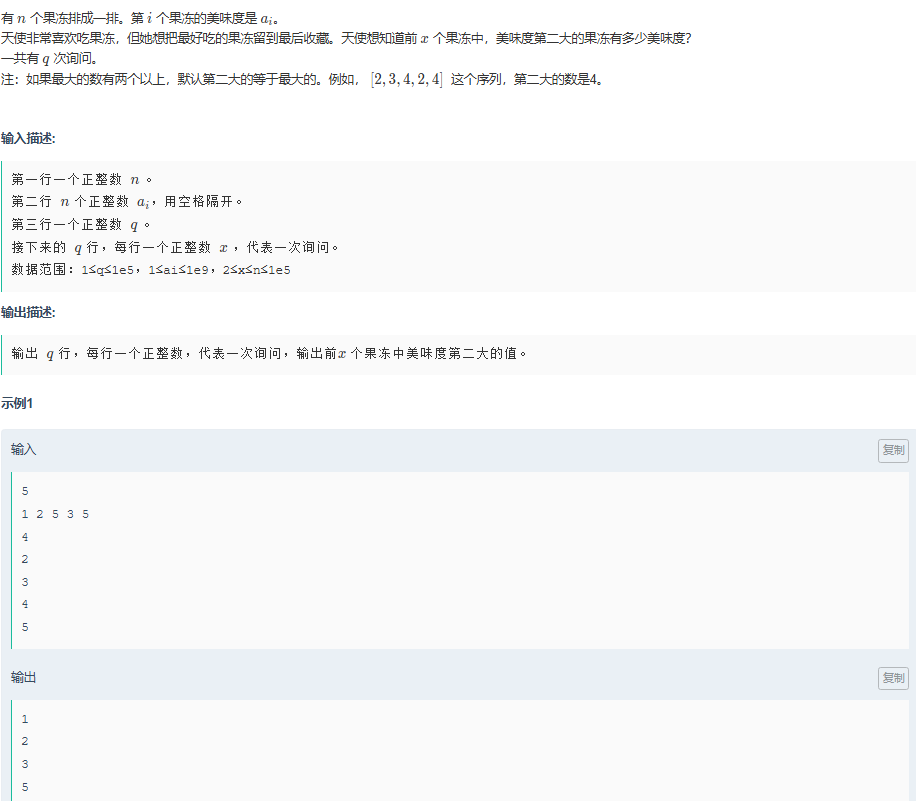
天使果冻

思路

模拟： 利用两个数组统计前i个位置的最大值和次大值，遍历数组并更新结果

代码

#include <iostream>
#include <vector>using namespace std;int main()
{int n; cin >> n;vector<int> a(n + 1);for(int i = 1; i <= n; i++) cin >> a[i];vector<int> f(n + 1); // 前 i 个的最大值；vector<int> g(n + 1); // 前 i 个的最小值；f[1] = a[1];for(int i = 2; i <= n ;i++){f[i] = max(f[i - 1], a[i]);if(a[i] > f[i - 1]) // 大于前一个位置的最大值{g[i] = f[i - 1];           }else if(a[i] > g[i - 1]) // 大于前一个位置的次大值{g[i] = a[i];}else{g[i] = g[i - 1];}}int q; cin >> q;while(q--){int x; cin >> x;cout << g[x] << endl;}return 0;
}

第二题

题目：

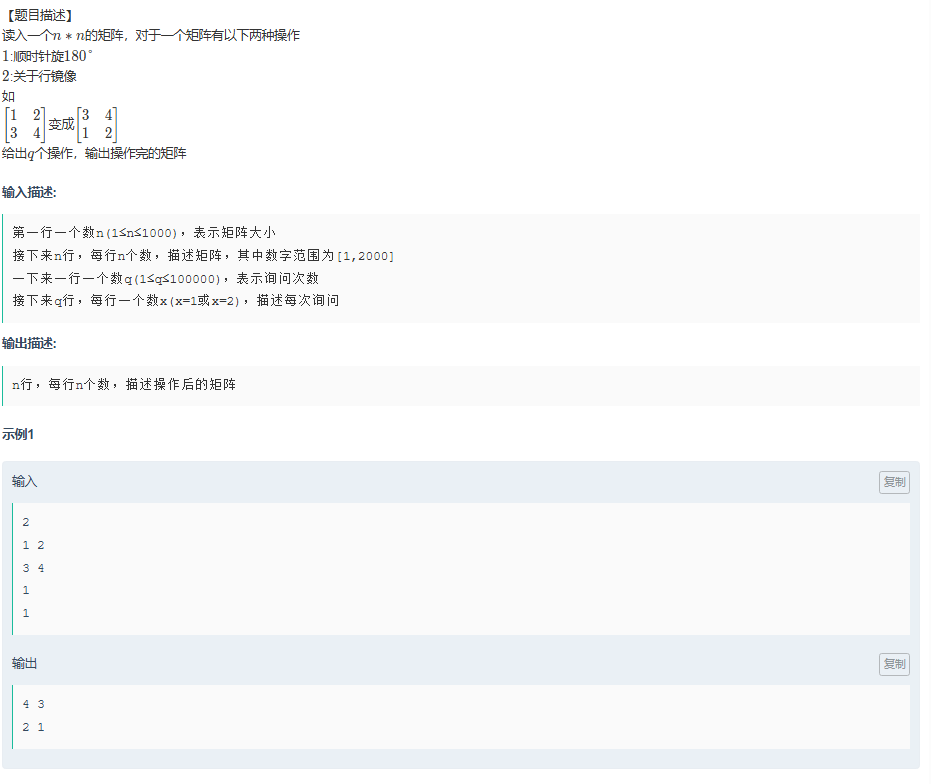
dd爱旋转

思路

模拟

• 顺指针180°等价于对矩阵进行行对称以及列对称
• 行镜像就是行对称；
• 统计x的个数，判断行对称以及列对称的次数，每两次会变回原状；所以可以优化减少变化次数；

代码

#include <iostream>
#include <vector>using namespace std;void Row(vector<vector<int>>& a) // 行
{int n = a.size();for(int i = 0; i < n / 2; i++){for(int j = 0; j < n; j++){swap(a[i][j], a[n - 1 - i][j]);}}
}void Col(vector<vector<int>>& a) // 列
{int n = a.size();for(int j = 0; j < n / 2; j++){for(int i = 0; i < n; i++){swap(a[i][j], a[i][n - 1 - j]);}}
}int main()
{int n; cin >> n;vector<vector<int>> a(n, vector<int>(n));for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){cin >> a[i][j];}}int q, x;cin >> q;int row = 0, col = 0;while(q--){int x = 0;cin >> x;if(x == 1) row++, col++;else row++;}row %= 2, col %= 2;if(row) Row(a);if(col) Col(a);for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){cout << a[i][j] << " ";}cout << endl;}return 0;
}

第三题

题目：

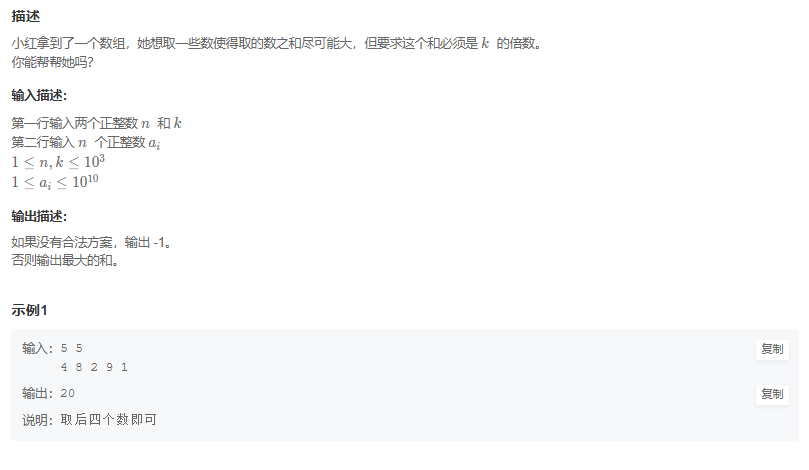
小红取数

思路

01背包

• 状态表示：dp[i][j]表示：从前i个数中选总和%k = j时最大的和；
• 状态转移方程：
  • 不选i位置，dp[i - 1][j]
  • 选i位置，dp[i - 1][(j - a[i] % k + k) % k] + a[i]

代码

#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1010;
int n, k;
LL a[N];
LL dp[N][N];
int main()
{cin >> n >> k;for (int i = 1; i <= n; i++)cin >> a[i];memset(dp, -0x3f, sizeof dp);dp[0][0] = 0;for (int i = 1; i <= n; i++){for (int j = 0; j < k; j++){dp[i][j] = max(dp[i - 1][j], dp[i - 1][(j - a[i] % k + k) % k] + a[i]);}}if (dp[n][0] <= 0)cout << -1 << endl;elsecout << dp[n][0] << endl;return 0;
}