算法篇----分治(归并排序)
一、归并排序
归并排序是一种分治算法,其基本思想是将一个大问题分解成若干个规模较小的子问题,递归地解决这些子问题,然后将子问题的解合并起来得到原问题的解。归并排序的效率较高,时间复杂度为O(n log n)。
二、步骤总结
1)归并排序通过递归将数组不断划分为更小的部分,直到每个部分只有一个元素,然后逐步合并 这些有序的部分,最终得到一个完全有序的数组。
2)归并排序的关键步骤是合并两个有序数组,这需要额外的空间(临时数组tmp)来存储合并结 果。
三、与快排的区别
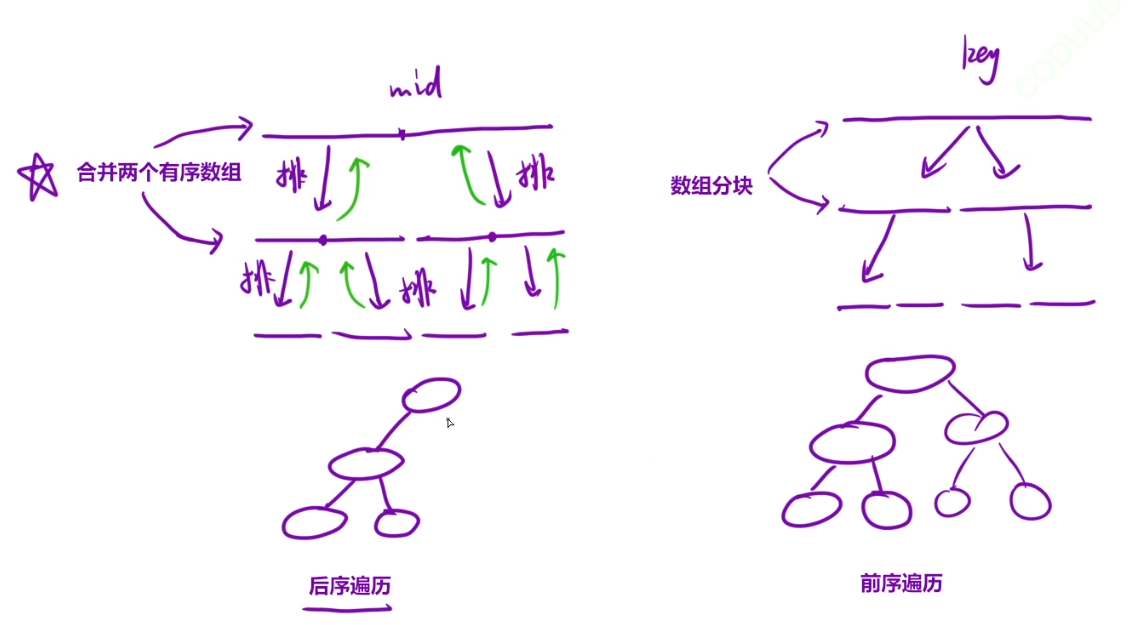
二者都是通过递归来进行排序,但不同的是快排需要选择一个基准点,之后左右开工一起排,而归并排序则是将数组不断划分至最小单元,之后从左向右不断递归排序,可以类比为二叉树的后序遍历,而快排可以类比为前序遍历
四、参考习题
1、 排序数组
912. 排序数组 - 力扣(LeetCode)
这是一个典型的归并排序算法的例题,看一下代码复习一下吧~
class Solution {vector<int> tmp; //造一个辅助数组,用于全局是会节省一点开销~
public:vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size()); //把辅助数组的容量给确定一下mergesort(nums,0,nums.size()-1);return nums;}void mergesort(vector<int>& nums,int left,int right){if(left>=right) return;//1.选择中间点划分区间int mid=(left+right)>>1;//[left,mid] [mid+1,right]//2.把左右区间排序mergesort(nums,left,mid);mergesort(nums,mid+1,right);//3.合并两个有序数组int cur1=left,cur2=mid+1,i=0;while(cur1<=mid && cur2<=right)tmp[i++]=nums[cur1]<nums[cur2]?nums[cur1++]:nums[cur2++]; //此举就是比较左右两个区间的数,依次选小的放入辅助数组中//可能有数组没有遍历完,处理一下while(cur1<=mid) tmp[i++]=nums[cur1++];while(cur2<=right) tmp[i++]=nums[cur2++];//4.还原for(int i=left;i<=right;i++)nums[i]=tmp[i-left];}
};2.交易逆序对的总数
LCR 170. 交易逆序对的总数 - 力扣(LeetCode)
解题思路:
如果暴力破解的话思路很简单,但是会超时,所以我们用分治的算法来解决一下,我们可以将数组划分成两段,之后先统计左端的逆序对个数,并进行排序,之后再统计右段的逆序对个数,并进行排序,最后再统计一左一右的逆序对个数。而左右两端的统计是通过不断递归来实现的~
在统计一左一右的逆序对个数时,我们左右两段的数组已经是排成升序的了,如图说是
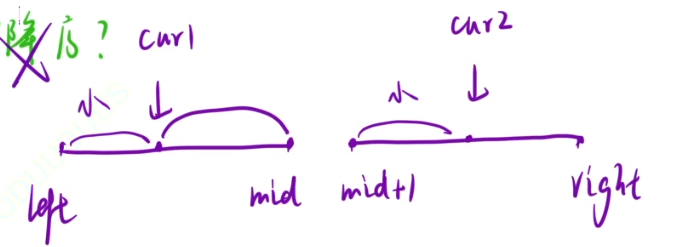
在cur1左侧的都比cur1小,cur2同理,那么我们只需要找到,当nums[cur1]<=nums[cur2]时,让cur1++,而当nums[cur1]>nums[cur2]时,让ret+=right-cur2+1即可,之后cur2++,继续该操作
class Solution
{int tmp[50010];
public:int reversePairs(vector<int>& nums) {return mergesort(nums,0,nums.size()-1);}int mergesort(vector<int>& nums,int left,int right){if(left>=right) return 0;int ret=0;//1.找中间点,将数组分为两端int mid=(left+right)>>1;//[left,mid] [mid+1,right]//2.左边个数+排序+右边个数+排序ret+=mergesort(nums,left,mid);ret+=mergesort(nums,mid+1,right);//3.一左一右计数int cur1=left,cur2=mid+1,i=0;while(cur1<=mid&&cur2<=right) {if(nums[cur1]<=nums[cur2]){tmp[i++]=nums[cur2++];}else{ret+=right-cur2+1;tmp[i++]=nums[cur1++];}}while(cur1<=mid) tmp[i++]=nums[cur1++];while(cur2<=right) tmp[i++]=nums[cur2++];for(int j=left;j<=right;j++){nums[j]=tmp[j-left];}return ret;}
};3.计算右侧小于当前元素的个数
解题思路:
这道题答题思路跟上一条差不多,但是增加的难的点是如何确定下标,更确切的说是如何保证下标和元素一直保持一一对应,为此我们可以仿照哈希表,在构造一个Index的数组,存放各个的下标,值得注意的是,元素在进行排序时,要记得对下标也进行对应的移动
class Solution
{vector<int> ret;vector<int> index;//// 记录 nums 中当前元素的原始下标int tmpindex[500010];int tmpnums[500010];
public:vector<int> countSmaller(vector<int>& nums) {int n=nums.size();ret.resize(n);index.resize(n);// 初始化⼀下 index 数组for(int i=0;i<n;i++){index[i]=i;}mergesort(nums,0,nums.size()-1);return ret;}void mergesort(vector<int>& nums,int left,int right){if(left>=right) return;int mid=(right+left)>>1;mergesort(nums,left,mid);mergesort(nums,mid+1,right);int cur1=left,cur2=mid+1,i=0;while(cur1<=mid&&cur2<=right) //降序{if(nums[cur1]<=nums[cur2]){tmpnums[i]=nums[cur2];tmpindex[i++]=index[cur2++];}else{ret[index[cur1]]+=right-cur2+1;tmpnums[i]=nums[cur1];tmpindex[i++]=index[cur1++];}}//4.处理剩下的排序过程while(cur1<=mid){tmpnums[i]=nums[cur1];tmpindex[i++]=index[cur1++];}while(cur2<=right){tmpnums[i]=nums[cur2];tmpindex[i++]=index[cur2++];}for(int j=left;j<=right;j++){nums[j]=tmpnums[j-left];index[j]=tmpindex[j-left];}}
};