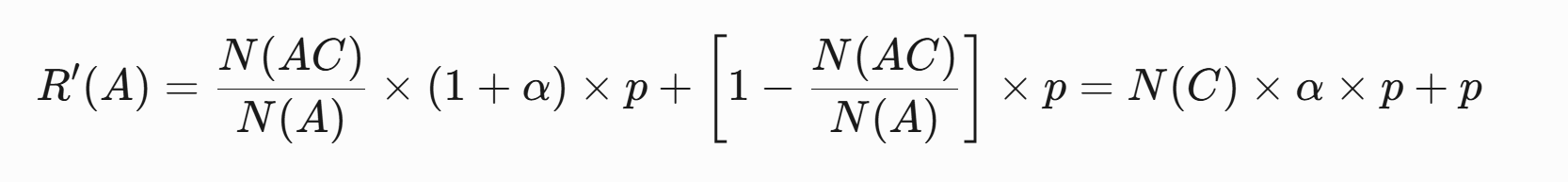当前位置：首页 > news >正文

第5章 AB实验的随机分流

news 2025/8/13 9:15:50

一、引言：本章概述

二、单层分流模式：实现与挑战

三、正交分层模式：流量复用与正交性

1. 正交性问题：如何保证层间独立性

2. 分层问题：如何设计层结构

四、散列算法：性能与评估

五、总结：关键要点回顾

一、引言：本章概述

在AB实验中，随机分流是确保实验可靠性的基础，核心目标是将用户公平随机地分配到实验组和对照组，从而准确测量策略效果。本章针对四个关键问题展开：用户随机分组机制、实验流量不足的解决、层间正交性的实现，以及散列算法的选择。

通过单层分流模式处理小规模实验需求，正交分层模式应对并发实验的流量复用挑战，并辅以散列算法保证分流的均匀性和独立性。这些方法在实践中需结合监控（如AA实验）来避免偏差。

二、单层分流模式：实现与挑战

解释用户随机分组方法、流量限制问题及解决方案。

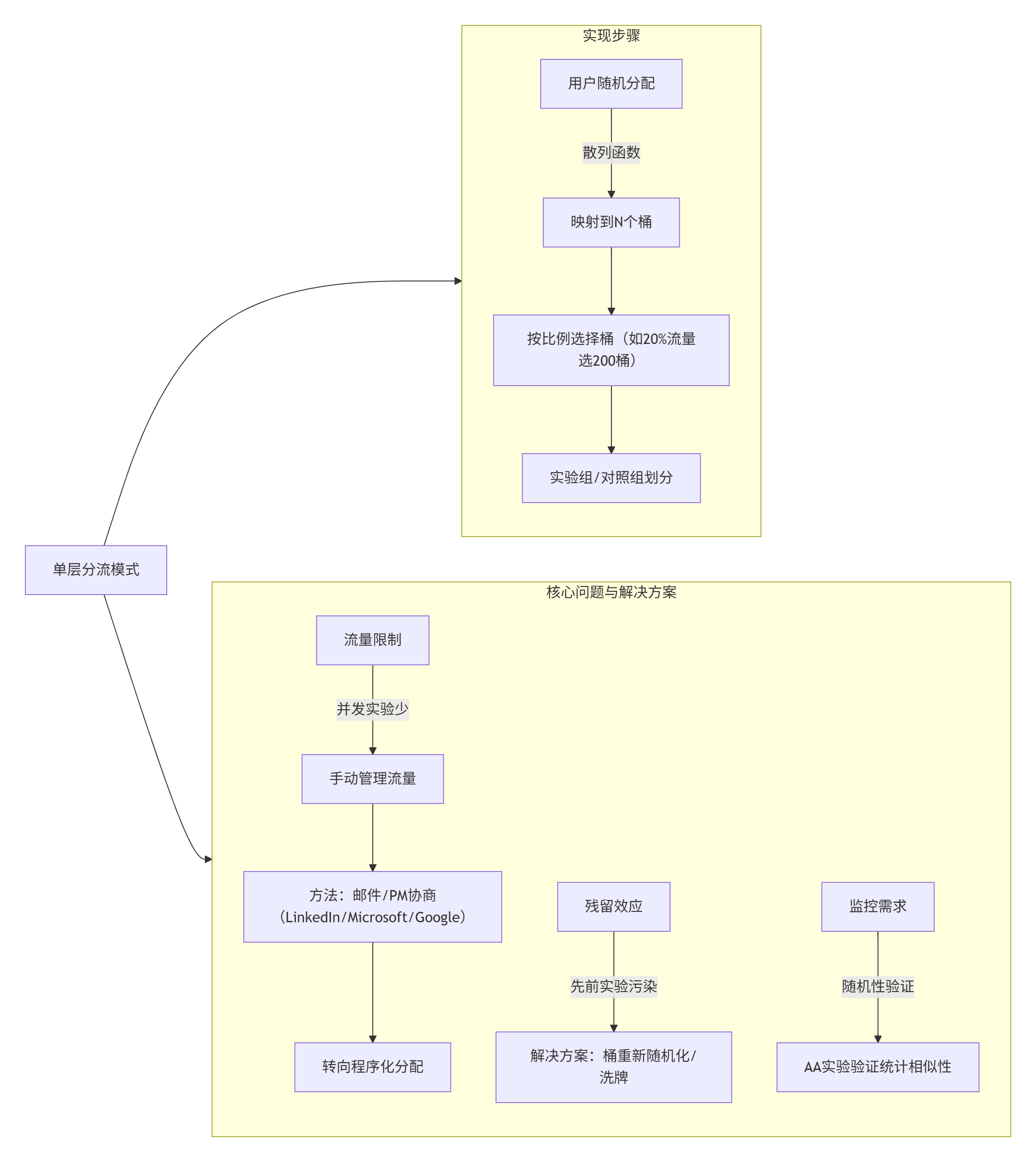
在AB实验的早期阶段，通常采用单层分流模式。该方法的核心是用户在同一时间内仅参与一个实验，确保实验单元的唯一性。以下是详细解释：

随机分组机制：使用散列函数（如MD或Murmur）将用户映射到固定数量的桶（buckets）中。例如，1000万用户通过散列函数分配到1000个桶，每个桶约10000用户。实验流量（如20%）通过随机选择对应比例的桶实现。关键在于：
- 随机性与确定性：散列过程必须是随机的（保证用户公平分布），但又是确定性的（相同用户每次映射到相同桶），确保实验可重复。
- 相似性验证：通过AA实验（第7章）验证桶间统计相似性，例如关键指标（如点击率）应大致相同，避免因用户分布不均导致偏差。
流量限制问题：单层模式下，实验流量（可用用户数量）有限，无法支持大量并发实验。LinkedIn、Microsoft和Google早期通过手动管理流量（如电子邮件协商），但效率低下。随着实验量增加，手动方法无法满足需求，需转向程序化分配（如自动化流量调度）。
常见问题与解决方案：
- 残留效应：先前实验可能污染当前桶（如策略遗留影响）。解决方案包括桶的重新随机化或洗牌（打乱桶顺序），避免连续分配。
- 监控重要性：Google等公司通过监控桶特征（如用户数量分布）发现随机化错误。配置AA实验或SRM校验可检测分流不均（如组间指标显著差异）。

单层模式简单易用，但限制了实验规模。下一节介绍的正交分层模式解决了这一瓶颈。

三、正交分层模式：流量复用与正交性

重点解析层间正交性的原理（包括数学推导）、分层策略和架构框架。

为解决单层模式流量不足的问题，正交分层模式允许用户同时参与多个实验，通过多层结构实现流量复用。核心在于层间正交性（independence），确保不同层实验互不干扰。

1. 正交性问题：如何保证层间独立性

正交性是什么？就是让不同层的实验互不干扰。

比如你在测试「按钮颜色」（层1）和「广告文案」（层2），正交性保证颜色实验不会影响文案实验的测量结果。

类比：像多层透明玻璃，每层图案叠加后互不遮挡（层1画红色，层2画条纹，最终看到的是红条纹，但红色不影响条纹的独立性）。

正交性指用户在各层中的分布均匀随机，使得层间影响相互抵消。例如，层1的实验A和层2的实验C正交时，实验C的效果不会干扰A的测量结果。

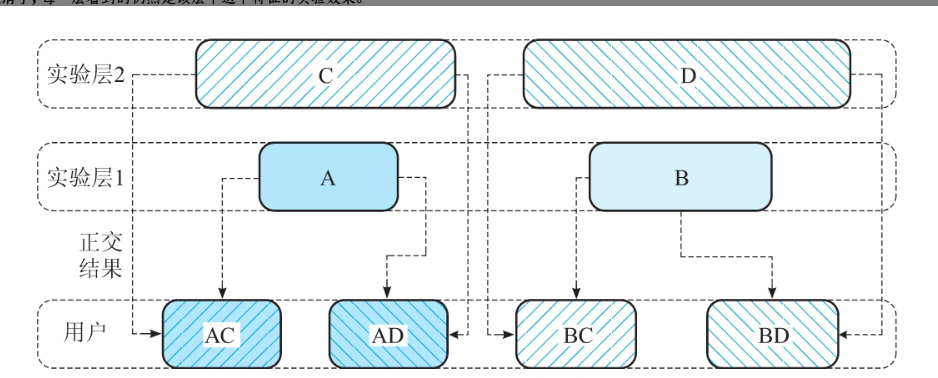
正交性原理：如果层1用户均匀随机分布到其他层，则层间影响被抵消。

观察指标：点击率

假设层1实验组A和B的流量比例分别为N(A)和N(B)，层2实验组C和D的流量比例为N(C)和N(D)。正交时，同时命中A和C的用户数量N(AC)应满足N(AC) = N(A) × N(C)。

当层2实验组C应用新策略（点击率提升α），其对层1实验组A的影响计算为：

实验组A、B、C、D都不应用任何策略时，R(A)=R(B)=R(C)=R(D)=p，R代表点击率。

假设实验层2的实验组C应用了新策略，点击率相对提升为α，那么此时R(C)=(1+α)×p。

实验组C对实验组A的影响分两部分，一部分是被C策略影响的用户N(AC)，效果为(1+α)×p，一部分是没有被C策略影响的用户1-N(AC)，效果仍然为p，此时原来A策略作用人群总效果，以R'表示

变化量。同理，实验C对B的影响ΔR(B)相同，因此在对比A和B时，C的效果被抵消。

正交计算案例

实验层1：10%用户命中组A（按钮红色），20%组B（按钮蓝色）。

实验层2：30%用户命中组C（文案“限时优惠”），40%组D（文案“新品上市”）。

正交组合占比=层1分组比例×层2分组比例

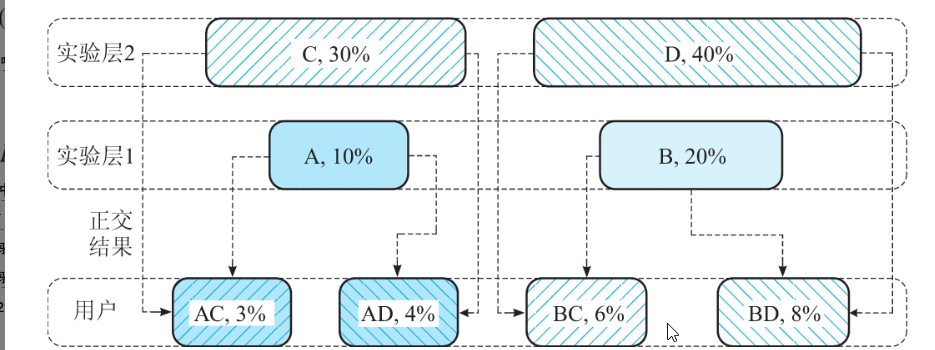
层1中10%用户命中A，层2中30%用户命中C，则同时命中A和C的用户比例为3%（即N(AC) = N(A) × N(C)）。分组比例保持一致（如N(A):N(B) = N(AC):N(BC)），证明正交性。

通过分层独立分配，确保实验效果可精准分离。若总用户为1000人：

同时命中A和C的用户数 = 1000 × 3% = 30人
同时命中B和D的用户数 = 1000 × 8% = 80人

层间无干扰：D组策略若提升10%点击率，对A、B组的影响是均匀的（A组+4%×10%，B组+8%×10%），对比A/B时差异抵消。

用“涨工资”理解影响抵消

假设公司给D组的人涨工资10%，会影响其他实验：

A组中有4%的人（AD块）涨了工资 → A组整体收入 +4%×10%=+0.4%

B组中有8%的人（BD块）涨了工资 → B组整体收入 +8%×10%=+0.8%

关键魔法：

当比较A组和B组的收入时：

A组收入 = A策略效果 + 0.4%

B组收入 = B策略效果 + 0.8%

A vs B差异 = (B策略 - A策略) + (0.8%-0.4%) = 真实差异 + 0.4%

但因为我们知道干扰量就是0.4%，直接减掉它，就能算出真实的A/B策略差异！

什么是“加盐”？

加盐（Salting）是实际实现层间正交性的关键技术手段。

简单说：加盐是通过在散列函数中加入层级标识符，确保同一用户在不同层的分组结果独立。

类比：就像给同一把钥匙（用户ID）配不同的锁芯（盐值），使得钥匙在不同房间（层）开不同的门（分组）。

具体操作：

原始散列：直接用用户ID散列 → 用户被随机分到桶（如桶1~100）。
加盐散列：用户ID + 层ID（如“UI层”）作为新输入 → 重新散列，得到完全不同的桶分布。
- 例如：
  - 用户123在UI层：hash("123_UI")→ 桶A
  - 同一用户在广告层：hash("123_AD")→ 桶B

若不加盐，用户在所有层使用相同的散列结果 → 导致层间分组强相关（如UI层桶A的用户永远在广告层桶A）。

加盐后，通过不同盐值（如“UI”、“AD”）打散关联性，实现图中标注的正交结果层比例（如AC=3%、BD=8%）。

2. 分层问题：如何设计层结构

分层策略旨在平衡流量复用和避免实验冲突（如参数碰撞导致用户体验差）。

分层原则：

同类业务互斥：改变同一类参数（如UI元素）的实验放入同一层，防止冲突。例如，UI层可细分为文字、颜色等子层，但避免过细拆分（如单独按钮颜色层），以免增加碰撞风险。
不同类业务正交：如UI层、搜索层、广告层拆分到不同层，通过正交保证层间隔离。流量复用允许用户同时参与多层实验（如最多3个）。

层域架构：

为支持复杂实验（如跨层联合测试），引入“域”（domain）概念。域代表未分层的流量，可嵌套层结构：例如，在穿透域（permeated domain）中，可进行跨层联合实验（如同时测试字体和颜色）。

图5-3展示了经典架构：a图是三层正交框架；b图添加穿透域，允许域内实验；c图引入发布域；d图为复杂嵌套框架。核心是域间实验互斥（用户仅在一个域中）。

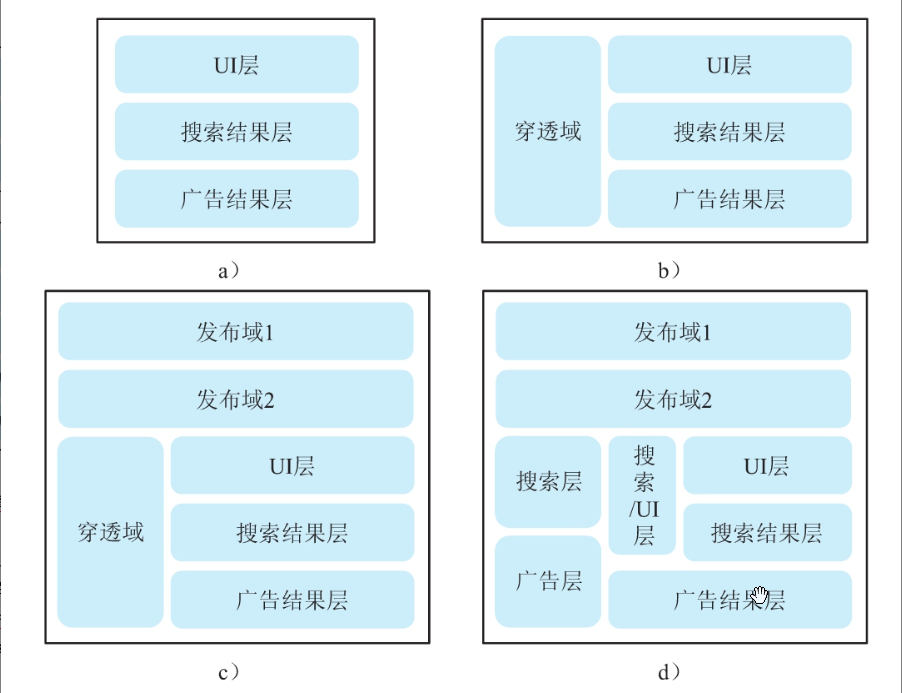
正交分层模式显著提升流量利用率，但需注意层数过多会增加碰撞概率。优化方案包括监控层间交互。

用“乐高积木”解释这张图

1. 核心概念拆解

域（Domain）：一整块完整的乐高底板（比如8×16的蓝色底板），代表未切分的原始流量池。
层（Layer）：在底板上拼出的独立乐高条（比如UI层、搜索层、广告层），每条代表一类实验的专属区域。
穿透域（Permeated Domain）：一块可以跨层穿透的特殊积木（如图b红色块），允许实验同时影响多层。

2. 四张子图详解

a图（正交层框架）：像把底板切成3条独立乐高层（UI/搜索/广告），每条层互不干扰，用户最多同时参与3个实验（每层1个）。

b图（穿透域+正交层）：底板被分成两大块：

左边红色穿透域：实验可跨层联动（如同时改UI和广告）。
右边正交层：和a图一样严格分层。
规则：用户不能同时踩在红色和蓝色区域！

c图（加入发布域）：新增黄色发布域：专门用于新功能灰度发布，和其他域严格隔离。

d图（复杂嵌套）：像多层乐高嵌套：大域里套小层，小层里再分域（如“广告层”内部分为“图文域”和“视频域”）。

3. 为什么这样设计？

正交层：保证实验独立性（如测试按钮颜色不影响搜索算法）。
穿透域：解决跨层联动的需求（如改UI必须同步改广告样式）。
发布域：避免新功能干扰AB测试结果。

4. 用户需记住的规则

实验不跨界：用户要么在穿透域，要么在正交层，不能两边蹭！
分层不超3：正交层中，用户最多同时参与3个实验（UI+搜索+广告各1个）。
域可无限套娃：大域里可以再分小层，小层里还能再切域。

5. 现实类比

正交层 ≈ 公司分部门（设计部、技术部、市场部），员工只能在一个部门领任务。
穿透域 ≈ 跨部门项目组（临时抽调各部门人员协作）。
发布域 ≈ 封闭开发的新产品线，和其他业务完全隔离。

四、散列算法：性能与评估

说明算法选择标准、常见类型及实际应用中的问题。

散列算法是实现随机分流的技术基础，影响分流的效率和质量。

评估指标：

计算性能：算法速度需快，以免影响线上响应（如Murmur算法性能优于MD）。
均匀性：用Hash_diff衡量组间用户数量差异：Hash_diff = (组间用户数量标准差) / (组间用户数量均值)。值越小，均匀性越好（理想为0）。
相关性：用Layer_diff衡量层间组交集差异：Layer_diff = (层间组交集标准差) / (层间组交集均值)。值越小，层间独立性越高。

目标：检查用户是否均匀分布到各实验组。

步骤：

将10,000用户分配到UI层的A/B组（各50%流量）。

统计A/B组实际用户数：

A组：4,950人

B组：5,050人

计算Hash_diff：

均值 = (4950 + 5050)/2 = 5000

标准差 = √[(4950-5000)² + (5050-5000)²]/2 = 50

Hash_diff = 50/5000 = 0.01（接近0，均匀性优秀）

问题案例：若A组4800人，B组5200人，则Hash_diff=0.04，需排查散列函数或分流逻辑。

目标：验证UI层和广告层的实验是否独立（正交性）。

步骤：

用户同时命中UI层（A/B组）和广告层（C/D组），统计交叉占比：

AC组：24.8%

AD组：25.2%

BC组：24.9%

BD组：25.1%

计算Layer_diff：

均值 = (24.8+25.2+24.9+25.1)/4 = 25%

标准差 = √[(24.8-25)² + (25.2-25)² + (24.9-25)² + (25.1-25)²]/4 ≈ 0.16

Layer_diff = 0.16/25 ≈ 0.0064（极低，层间独立性高）

问题案例：若AC组占30%，BD组占20%，则Layer_diff=0.2，表明层间存在干扰，需检查散列盐值（Salt）是否按层区分。

常见算法：MD、SHA、JDB、Murmur等。Murmur最常用，因其高性能、强抗碰撞性（均匀性和相关性最优）。

实际挑战：尽管算法理论上保证均匀，实际中可能出现分流不均（如用户行为差异或系统错误）。检测方法：

SRM校验或AA实验：运行无策略差异的实验，监控指标显著差异（如组间点击率不一致）。
原因包括高活跃用户分布不均或遗留实验影响。建议实验前必做基础校验。

散列算法是分流系统的核心，需结合业务场景优化选择。

五、总结：关键要点回顾

本章系统解析了AB实验随机分流的关键机制：

单层分流模式：适合小规模实验，通过散列函数随机分配用户到桶，但面临流量限制和残留效应问题，需监控和程序化管理。
正交分层模式：解决流量复用问题，核心是层间正交性（通过加盐值散列保证），确保实验独立。分层策略（有限层+域架构）避免冲突，提升扩展性。
散列算法：优先选择高性能、高均匀性算法（如Murmur），并通过Hash_diff和Layer_diff评估质量。实践中需防范分流不均。
整体启示：随机分流不仅是技术实现，更需结合统计监控（如AA实验）和业务理解。Google、LinkedIn等公司的经验证明，自动化分层和算法优化是支撑大规模实验平台的关键。

来源书籍：——刘玉凤《AB实验：科学归因于增长的利器》