当前位置：首页 > news >正文

LCR 120. 寻找文件副本

news 2025/8/12 7:07:32

题目链接：

题目：

代码：

总结：

题目链接：

LCR 120. 寻找文件副本 - 力扣（LeetCode）

题目：

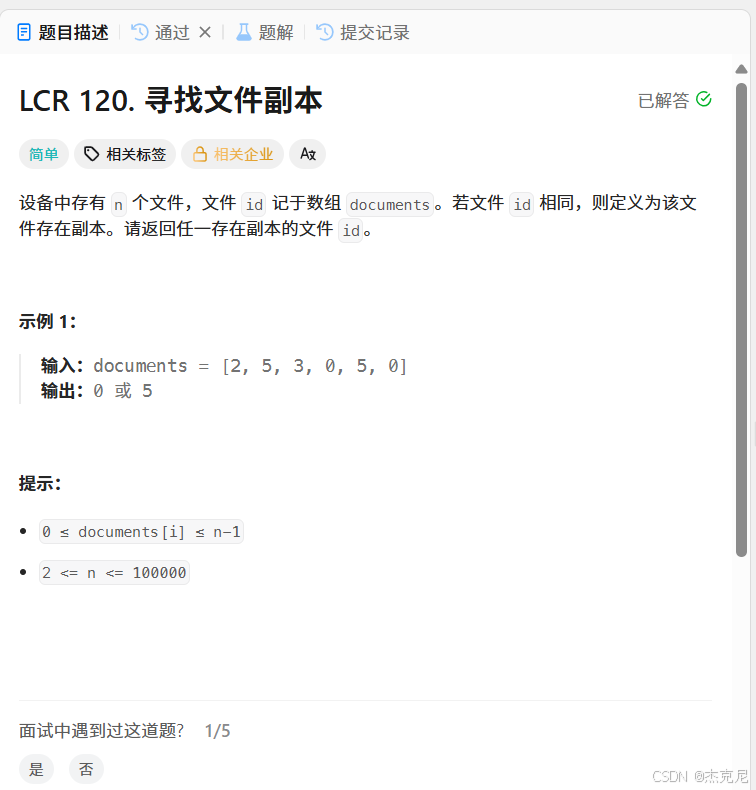
LCR 120. 寻找文件副本

已解答

简单

相关企业

设备中存有 n 个文件，文件 id 记于数组 documents。若文件 id 相同，则定义为该文件存在副本。请返回任一存在副本的文件 id。

示例 1：

输入：documents = [2, 5, 3, 0, 5, 0]
输出：0 或 5

提示：

0 ≤ documents[i] ≤ n-1
2 <= n <= 100000

解题思路：

数组重复元素查找代码深度解析

这段 Java 代码出自 Solution 类的 findRepeatDocument 方法，核心功能是在给定的整数数组 documents 中查找并返回任意一个重复出现的元素。代码通过 “排序 + 遍历比对” 的思路实现需求，逻辑清晰且易于理解，以下从功能定位、实现步骤、设计思路、优缺点等维度展开详细解析。

一、功能定位与核心需求

该方法的输入是一个整数数组 documents，输出是数组中任意一个重复出现的元素；若数组中无重复元素（根据题目场景通常不会出现），则返回 0。
从方法名 findRepeatDocument 推测，这可能是一道算法题的解决方案（例如 “找出数组中重复的数字” 类题目），核心需求是高效定位重复元素，无需返回所有重复元素，只需找到任意一个即可。

二、代码实现步骤拆解

代码仅用 5 行核心逻辑完成功能，步骤清晰，可拆解为 “排序预处理” 和 “遍历比对找重复” 两个关键阶段：

1. 数组排序：Arrays.sort(documents);

这一步是整个算法的 “预处理阶段”，通过 Java 内置的 Arrays.sort() 方法对输入数组 documents 进行升序排序。

排序的作用：将数组中相同的元素 “聚集” 在一起。例如，原数组 [2, 3, 1, 0, 2, 5, 3] 排序后会变为 [0, 1, 2, 2, 3, 3, 5]，重复元素 2 和 3 分别相邻排列，为后续查找重复元素奠定基础。
排序算法选择：Arrays.sort() 在 Java 中根据数组元素类型和长度自动选择最优排序算法（例如对整数数组，通常使用双轴快速排序或归并排序），时间复杂度为 O(n log n)（n 为数组长度），确保排序效率稳定。

2. 遍历比对：查找相邻重复元素

排序完成后，通过循环遍历数组，对比相邻元素是否相等，找到第一个重复元素即返回：

java

运行

for (int i = 1; i < documents.length; i++) {if (documents[i] == documents[i - 1]) {return documents[i];}
}
return 0;

循环逻辑：
循环从索引 i = 1 开始（因为要对比当前元素与前一个元素），遍历至数组末尾（i < documents.length）。每次循环中，通过 documents[i] == documents[i - 1] 判断当前元素与前一个元素是否相同。
终止条件：一旦发现相邻元素相等（即 documents[i] == documents[i - 1]），说明找到重复元素，立即返回该元素（return documents[i]），无需继续遍历，保证效率。
边界处理：若循环结束后未找到任何重复元素（理论上的极端情况），方法返回 0 作为默认值，避免无返回值的编译错误。

三、设计思路与核心逻辑解析

该方法的核心设计思路是利用 “排序后重复元素相邻” 的特性简化查找过程，将 “无序数组中找重复” 的复杂问题转化为 “有序数组中找相邻相等元素” 的简单问题，具体逻辑链如下：

无序数组的痛点：在未排序的数组中查找重复元素，通常需要逐个遍历并记录已出现的元素（如用哈希表存储），否则难以高效判断元素是否重复。
排序的价值：排序后，相同元素必然连续排列（例如 [1, 2, 2, 3] 中两个 2 相邻），无需额外空间记录已出现元素，只需对比相邻元素即可。
遍历的高效性：排序后遍历数组的时间复杂度为 O(n)（n 为数组长度），加上排序的 O(n log n)，整体时间复杂度为 O(n log n)，在多数场景下属于高效解法。

四、优缺点分析

优点：

实现简单，易于理解：代码仅依赖排序和一次遍历，逻辑直观，无需复杂的数据结构或算法知识，新手也能快速掌握。
无需额外空间（除排序开销外）：排序过程虽可能占用一定内存（取决于排序算法），但相比 “哈希表法”（需额外 O (n) 空间存储元素出现次数），空间复杂度更优（若忽略排序的临时空间，可视为 O (1)）。
适用于多数场景：对于中等规模的数组（如长度在 10^5 以内），O(n log n) 的时间复杂度完全可接受，且 Java 内置排序方法经过高度优化，实际运行效率较高。

缺点：

修改原数组结构：排序会改变原数组中元素的位置，若题目要求 “不能修改输入数组”，则该方法不适用（例如某些场景需保留数组原始顺序）。
时间复杂度依赖排序：对于超大规模数组（如长度 10^6 以上），O(n log n) 的排序时间可能略逊于哈希表的 O(n) 时间复杂度（哈希表法通过一次遍历即可找到重复元素）。
仅返回第一个重复元素：由于找到第一个相邻重复元素后立即返回，无法获取所有重复元素，但题目需求仅需 “任意一个重复元素”，因此不影响功能。

五、适用场景与优化方向

适用场景：

题目允许修改输入数组（排序会改变原数组顺序）。
对空间复杂度有要求（需避免使用额外哈希表等数据结构）。
数组规模中等，O(n log n) 时间复杂度可接受。

优化方向（可选）：

处理原数组不可修改的场景：若需保留原数组顺序，可复制一份数组进行排序，避免修改输入（代价是额外 O (n) 空间）。
提升极端规模下的效率：对于超大规模数组，可改用 “哈希表法”：遍历数组时用 HashSet 记录已出现元素，若当前元素已在集合中，则返回该元素，时间复杂度优化为 O (n)，但需额外 O (n) 空间。
边界条件增强：可添加对输入数组的校验（如 if (documents == null || documents.length <= 1) return 0;），避免空数组或长度为 1 的数组进入循环，增强代码健壮性。

六、示例验证

为直观理解代码逻辑，以具体示例演示执行过程：

输入数组：documents = [3, 1, 2, 3, 4]
步骤 1：排序后数组变为 [1, 2, 3, 3, 4]。
步骤 2：遍历数组：
- i=1：documents[1]=2 与 documents[0]=1 不相等，继续。
- i=2：documents[2]=3 与 documents[1]=2 不相等，继续。
- i=3：documents[3]=3 与 documents[2]=3 相等，返回 3。
输出结果：3（正确找到重复元素）。

总结

这段代码通过 “排序 + 相邻比对” 的经典思路，简洁高效地解决了 “查找数组中任意重复元素” 的问题。其设计巧妙利用排序的特性简化查找逻辑，实现成本低且易于维护，适合多数中等规模数组的场景。尽管存在修改原数组、时间复杂度依赖排序等局限性，但在满足题目约束的前提下，是一种性价比很高的解决方案，也体现了 “预处理（排序）简化问题” 的算法设计思想。

代码：

class Solution {public int findRepeatDocument(int[] documents) {Arrays.sort(documents);for(int i=1;i<documents.length;i++){if(documents[i]==documents[i-1]){return documents[i];}}return 0;}
}

总结：

本文解析了LCR120题"寻找文件副本"的Java解法。该算法通过排序预处理（时间复杂度O(nlogn)）和遍历比对（O(n)）两个步骤，在数组中查找任意重复元素。核心思路是利用排序后相同元素相邻的特性，通过比较相邻元素快速定位重复项。该方法实现简单、空间效率高（仅需排序开销），适用于中等规模数组。但存在修改原数组的局限性，且仅返回首个发现的重复元素。文章还探讨了优化方向，如处理不可修改数组的场景或使用哈希表法提升效率。示例验证展示了算法的执行过程，证实了其有效性。

查看全文

http://www.dtcms.com/a/325768.html