C4.5算法:增益率(Gain Ratio)
目录
1、为什么要改进信息增益?
2、增益率的数学本质
公式
案例
3、计算实例分步演示
数据集
第一步:计算原始信息熵
第二步:计算各特征信息增益
1. 特征"天气"(3个取值)
2. 特征"风速"(2个取值)
第三步:特征选择对比
第四步:验证多值特征惩罚
4、C4.5的完整改进措施
(1)处理连续特征(解决数值型数据问题)
(2)处理缺失值(解决数据不完整问题)
(3)后剪枝(解决过拟合问题)
三者的内在联系
5、业务应用中的特殊处理
"信息增益率是给信息增益装上刹车片,防止它冲向多值特征的悬崖"
1、为什么要改进信息增益?
信息增益(ID3算法)存在严重偏差:它会优先选择取值数目多的特征(如"用户ID"这种唯一值特征),但这会导致:
- 无效分裂:每个ID对应一个样本,Gain达到最大值但毫无预测能力
- 过拟合风险:生成过于复杂的树结构
示例:在员工离职预测中:
- 特征A(部门):5个取值 → Gain=0.3
- 特征B(员工ID):1000个唯一值 → Gain=1.0
ID3会错误地选择B作为根节点
2、增益率的数学本质
公式
C4.5算法用增益率(Gain Ratio) 修正这一问题,公式为:
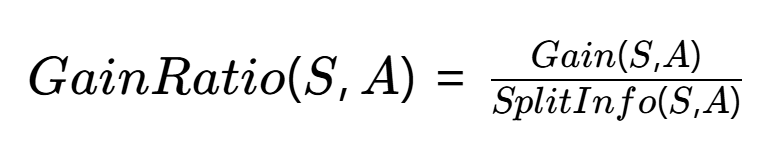
其中分裂信息(Split Information):
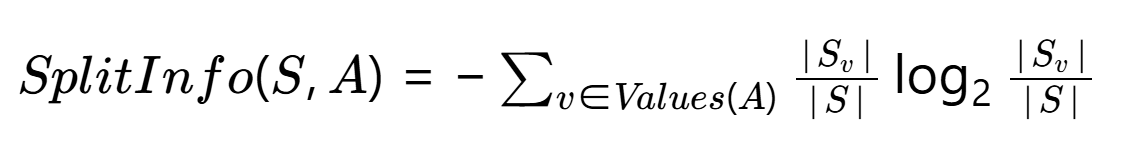
关键点:
- 分子:原始信息增益
- 分母:特征A本身的信息熵(惩罚多值特征)
- 当特征取值均匀分布时,SplitInfo达到最大值
案例
想象你在水果摊挑西瓜,老板让你用最少的提问找出最甜的瓜。增益率就是帮你衡量"每个提问的价值"的智能计算器。
1️⃣ 信息增益 = 提问带来的信息量
- 你问:"是红瓤吗?"(可能筛掉一半不甜的瓜)
- 信息增益就是这个问题帮你减少的不确定性
2️⃣ 分裂信息 = 问题本身的复杂程度
- 如果问:"瓜的编号是多少?"(每个瓜编号唯一)
- 这个问题太"细致"了,虽然能精准找瓜,但没实际意义
- 分裂信息就会很大,表示问题本身太复杂
3️⃣ 增益率 = 真正的有效信息量
就像老板会提醒你:
- "问颜色"(增益率0.8)比"问编号"(增益率0.01)更划算
- "问产地"(增益率0.3)不如"问敲声"(增益率0.6)有效
增益率就是防止你被"假聪明问题"忽悠的计算器——有些问题看似能精确分类(比如问身份证号),实际上对挑西瓜毫无帮助。
3、计算实例分步演示
数据集
| 天气 | 风速 | 打球 |
|---|---|---|
| 晴 | 弱 | 否 |
| 晴 | 强 | 否 |
| 阴 | 弱 | 是 |
| 雨 | 强 | 是 |
| 雨 | 弱 | 是 |
| 雨 | 强 | 否 |
第一步:计算原始信息熵
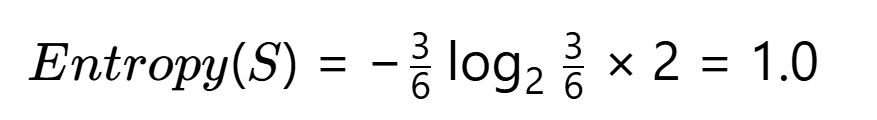
第二步:计算各特征信息增益
1. 特征"天气"(3个取值)
子集划分:
- 晴:2否 → Entropy=0
- 阴:1是 → Entropy=0
- 雨:2是1否 → Entropy=0.918
条件熵:![]()
信息增益:![]()
分裂信息:![]()
增益率:![]()
2. 特征"风速"(2个取值)
子集划分:
- 弱:1否2是 → Entropy=0.918
- 强:2否1是 → Entropy=0.918
条件熵:![]()
信息增益:![]()
分裂信息:![]()
增益率:![]()
第三步:特征选择对比
| 特征 | 信息增益 | 增益率 |
|---|---|---|
| 天气 | 0.541 | 0.371 |
| 风速 | 0.082 | 0.082 |
决策:选择增益率更高的"天气"作为分裂节点
第四步:验证多值特征惩罚
假设新增无关特征"日期"(5个唯一值):
计算SplitInfo(日期):
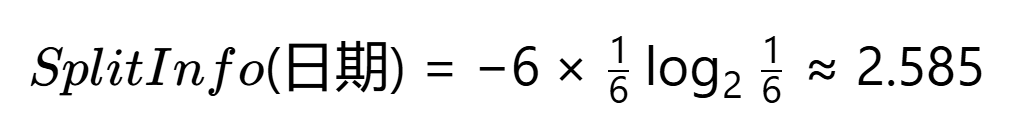
即使Gain(日期)=0.971(最大可能值):
![]()
实际选择:虽然"日期"增益率(0.387) > "天气"(0.371),但:
- 业务上排除无意义特征
- 可设置增益率阈值(如>0.4)过滤伪特征
关键结论
- 增益率机制:有效压制了"风速"等弱特征和"日期"等伪特征
- 计算本质:用特征自身熵对信息增益进行标准化
- 业务价值:选择天气(晴/阴/雨)作为首分裂特征,符合"恶劣天气不打球"的常识
4、C4.5的完整改进措施
(1)处理连续特征(解决数值型数据问题)
核心思想:将"年龄"这类连续数字变成可分类的阈值点
具体操作:
- 排序所有取值(如年龄[22, 25, 30])
- 计算相邻值中点(→23.5, 27.5)
- 将这些中点作为候选分割阈值
示例:用年龄预测是否购买保险:
- 测试条件1:年龄≤23.5?
- 测试条件2:年龄≤27.5?
- 选择信息增益率最高的分割点
业务意义:自动找到关键年龄分界点(如27.5岁可能是消费习惯转变的临界值)
(2)处理缺失值(解决数据不完整问题)
核心思想:按已知数据的比例"分配"缺失样本
具体操作:
- 计算已知数据的类别分布(如A类60%,B类40%)
- 将缺失样本按此比例分配到各分支
示例:
10个客户数据预测:
- 8个已知数据:5个A类(62.5%),3个B类(37.5%)
- 2个缺失数据:
- 1.25个(≈1个)分到A类分支
- 0.75个(≈1个)分到B类分支
(3)后剪枝(解决过拟合问题)
核心思想:先长完整棵树,再修剪掉不可靠分支
具体操作:
- 用训练集生成完整决策树
- 用验证集测试每个子树:
- 如果替换为叶节点能提升验证集准确率
- 则剪掉该子树
示例:某子树规则
温度>30? ├─ 是 → 湿度<50%? → 分类A └─ 否 → 分类B验证发现:
- 直接合并为"温度>30? → 分类A/分类B"准确率更高
- 则剪除"湿度"判断分支
三者的内在联系
- 连续特征处理:扩展算法应用范围(数值型数据)
- 缺失值处理:增强算法鲁棒性(现实数据总有缺失)
- 后剪枝:提升模型泛化能力(防止记住噪声)
完整工作流图示:

5、业务应用中的特殊处理
当遇到极端多值特征(如城市名称)时:
- 业务分组:将取值按业务逻辑合并(如一线/二线城市)
- 统计合并:将低频取值合并为"其他"类别
- 特征重要性筛选:先计算所有特征的增益率,人工剔除异常值
通过这种改进,C4.5算法实现了:
- 抗多值干扰:避免选择无意义的细分特征
- 更好的泛化性:生成的决策规则更具普适性
- 业务可解释性:分裂特征更符合业务逻辑
