当前位置：首页 > news >正文

机器学习第七课之支持向量机SVM

news 2025/8/10 8:13:04

简介：

欢迎来到机器学习系列课程的第七课！在这一课中，我们将聚焦于支持向量机（SVM） 这一经典且极具影响力的算法。作为监督学习领域的重要工具，SVM 凭借其出色的泛化能力和在小样本、高维空间中的优异表现，至今仍被广泛应用于图像识别、文本分类、生物信息学等多个领域。本节将从 SVM 的基本原理讲起，带大家理解它如何通过寻找最优超平面来实现数据分类 —— 这一超平面不仅能将不同类别的样本清晰分隔，还能使两类样本到超平面的最小距离（间隔）最大化，从而提升模型的稳定性。我们会深入剖析 “支持向量” 的核心概念，揭示这些关键样本点如何决定超平面的位置，以及它们在模型训练中的特殊作用。此外，面对线性不可分的数据，SVM 的核函数技巧堪称 “点睛之笔”。我们将详细解读线性核、多项式核、径向基核（RBF）等常用核函数的原理，展示它们如何将低维空间中线性不可分的数据映射到高维空间，进而实现线性可分。同时，还会探讨正则化参数（C）对模型复杂度和泛化能力的影响，帮助大家掌握 SVM 的调优思路。

一、什么是支持向量机

很久以前的情人节，公主被魔鬼绑架了，王子要去救公主，魔鬼和他玩了一个游戏。魔鬼在桌子上似乎有规律放了两种颜色的球，说：“你用一根棍分开它们？要求：尽量在放更多球之后，仍然适用。”

第一次，王子这么放：

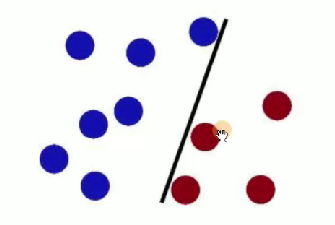
魔鬼又摆了更多的球，有一个球站错了阵营：

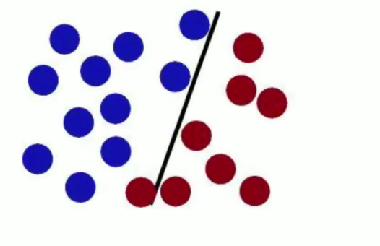
SVM 试图把棍子放在最佳位置，使棍两边有尽可能大的间隙。

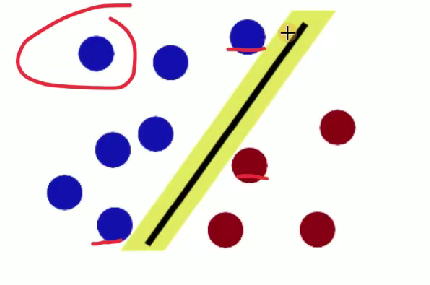
魔鬼放更多球后，棍仍能作为好的分界线，体现 SVM 对数据分类的有效性与泛化能力。

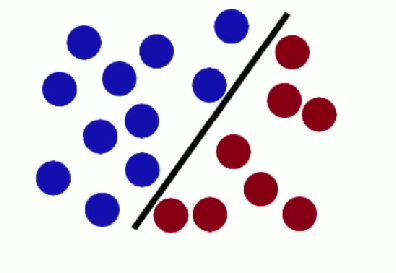
魔鬼使花招重新摆放球，王子拍桌让球飞起，拿纸插在两种颜色球中间，用于形象阐释 SVM 处理线性不可分等情况时的核函数等思想（将低维线性不可分数据映射到高维实现线性可分，类似把球 “升维” 后用平面分隔）。

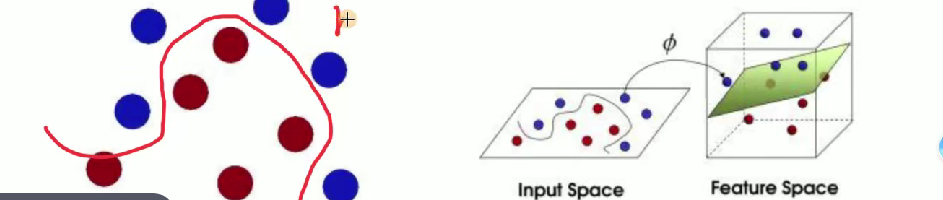
解释 SVM（支持向量机）相关概念

球 -> [data -> 数据]
棍子 -> [classifier -> 分类器]
最大间隙 trick -> [optimization -> 最优化]
拍桌子 -> [kernelling -> 核函数]
那张纸 -> [hyperplane -> 超平面]

二、如何选取最佳的超平面

对于这个图片我们去寻找

1.超平面方程 (优化目标)

样本点假设

假设有一堆样本点 $(x_1,y_1), (x_2,y_2), (x_3,y_3), \dots, (x_n,y_n)$

不同维度平面方程

二维平面：
- 常规直线方程： $y = kx + b$
- 转化后的形式： $Ax_1 + Bx_2 + C = 0$ ，备注 “一条线”
三维平面：
- 方程： $Ax_1 + Bx_2 + Cx_3 + D = 0$ ，备注 “平面”
更高维平面（超平面）：
- 方程： $\omega_1x_1 + \omega_2x_2 + \omega_3x_3 + \cdots + \omega_nx_n + b = 0$ ，备注 “超平面”

综合超平面函数

$\omega^t\Phi(x) + b = 0$ ，右侧备注 “ $\Phi(x)$ 看作x”

标签问题

在 SVM 中我们不用 0 和 1 来区分，使用 + 1 和 - 1 来区分，这样会更严格。假设超平面可以将训练的样本正确分类，那么对于任意样本：如果 $y = +1$ ，则称为正例， $y = -1$ ，则称为负例。

决策函数： $y(x) = sign(\omega^t \phi(x) + b)$

符号函数

$sign(x) = \begin{cases} -1, & x < 0 \\ 0, & x = 0 \\ 1, & x > 0 \end{cases}$

整合

决策函数

$y(x) = sign(\omega^t \Phi(x) + b)$

样本点分类正确的情况

当样本点分类正确的时候，有:

若 $y(x_i) > 0$ ，则 $y = +1$ （正例）
若 $y(x_i) < 0$ ，则 $y = -1$ （负例）

整合结果

$y \cdot y(x_i) > 0$

距离问题:

（1）点到直线的距离

$d = \frac{|\omega_1 x_1 + \omega_2 x_2 + b|}{\sqrt{\omega_1^2 + \omega_2^2}}$

（2）点到平面的距离

$d = \frac{|\omega_1 x_1 + \omega_2 x_2 + \omega_3 x_3 + b|}{\sqrt{\omega_1^2 + \omega_2^2 + \omega_3^2}}$

（3）点到超平面的距离

$d = \frac{|\omega_1 x_1 + \omega_2 x_2 + \omega_3 x_3 + \cdots + \omega_n x_n + b|}{\sqrt{\omega_1^2 + \omega_2^2 + \omega_3^2 + \cdots + \omega_n^2}}$

简写为： $y(x_i) = \frac{1}{||\omega||} (\omega^t \Phi(x_i) + b)$ ，其中 $||\omega||$ 是 $\omega$ 的范数， $\Phi(x_i)$ 是样本 $(x_i$ 的映射。这是 SVM 中关于点到超平面距离的数学表达，用于后续优化间隔等操作。

改进:

对公式加上正确性： $y(x_i) = \frac{1}{||\omega||} y_i (\omega^t \phi(x_i) + b)$

分类正确条件

分类正确时： $y_i \cdot y(x_i) > 0$

两个衡量指标

(1) 确信度：点到超平面距离
(2) 正确性：分类正确

2.如何寻找最优的超平面

步骤（1）：找到离超平面最近的点

$y(x_i) = \min_{i = 1, \dots, N} \frac{1}{||w||} y_i (\omega^t \Phi(x_i) + b)$

步骤（2）：最大化这个距离

$(\max_{\omega, b} [y(x_i)]$

使得离超平面最近的点到超平面的距离越远越好。

最终构成损失函数求解

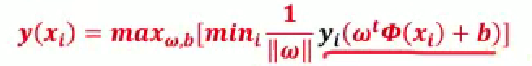
步骤（1）：设定最小值

令 $\min(y_i (\omega^t \Phi(x_i) + b)) = 1$ ，右侧原因说明：因分类正确时 $y_i (\omega^t \Phi(x_i) + b) \geq 0$ ，经放缩变换可使 $y_i (\omega^t \Phi(x_i) + b) \geq 1$ ，让条件更严格。

步骤（2）：转化优化目标

则优化目标变为 $\underset{\omega, b}{\text{argmax}} \frac{1}{||\omega||}$ 且 $y_i (\omega^t \Phi(x_i) + b) \geq 1$ ，即要在满足 $y_i (\omega^t \Phi(x_i) + b) \geq 1$ 的约束下，最大化 $\frac{1}{||\omega||}$ ，等价于最小化 $||\omega||$ ，这是 SVM 损失函数求解及优化目标转换的关键步骤。

拉格朗日乘子法:

求解有约束条件的极值问题

函数： $\min(f(x))$
约束条件： $s.t. g_i(x) \leq 0 (i = 1,2, \dots )$

对应 SVM 的目标与约束

$\underset{\omega, b}{\text{argmax}} \frac{1}{||\omega||}$

$y_i(\omega^t \phi(x_i) + b) \geq 1$

修改目标函数与约束条件相关内容

原目标函数：

${\text{argmax}} \frac{1}{||\omega||}$

转化后：

${\text{min}} \frac{1}{2} ||\omega||^2$ （极值点不变）

经过一系列的操作得到

3.举例分析

对于svm的推导公式实在晦涩难懂，我们直接讲述一个案例就好理解了。已知如图所示训练数据集，求最大间隔分离超平面。

正例点： $x_1 = (3,3)^T$ ， $x_2 = (4,3)^T$
负例点： $x_3 = (1,1)^T$

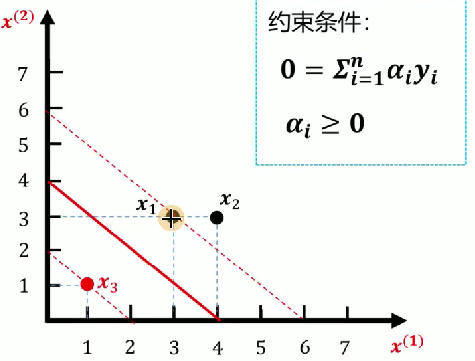
1.数据点代入公式

$\min_{\alpha} \frac{1}{2}(18\alpha_1^2 + 25\alpha_2^2 + 2\alpha_3^2 + 42\alpha_1\alpha_2 - 12\alpha_1\alpha_3 - 14\alpha_2\alpha_3) - \alpha_1 - \alpha_2 - \alpha_3$

2.添加约束

等式约束： $\alpha_1 + \alpha_2 - \alpha_3 = 0$ ，推出 $\alpha_3 = \alpha_1 + \alpha_2$
不等式约束： $\alpha_i \geq 0, i = 1,2,3$

3.代入化简

化简后的式子： $4\alpha_1^2 + \frac{13}{2}\alpha_2^2 + 10\alpha_1\alpha_2 - 2\alpha_1 - 2\alpha_2$ ，通过求最小值（求偏导方式）进一步处理。

对 $\boldsymbol{\alpha_1}$ 和 $\boldsymbol{\alpha_2}$ 求偏导等于 0

计算得 $\alpha_1 = 1.5$ （满足 $\alpha_i \geq 0$ ）
$\alpha_2 = -1$ （不满足 $\alpha_i \geq 0$ ）

4.条件判断

因 $\alpha_2 = -1$ 不满足条件，对应超平面方程不可取（强调先决条件必须满足）

5.思考

解不在偏导为 0 的位置，应在边界上（ $\alpha_1$ 或 $\alpha_2$ 等于 0 ）

令 $\boldsymbol{\alpha_1}$ 或 $\boldsymbol{\alpha_2}$ 等于 0

当 $\alpha_1 = 0$ 时：代入原式得 $\frac{13}{2}\alpha_2^2 - 2\alpha_2$ ，求偏导后得 $\alpha_2 = \frac{2}{13}$ ，再代入原式求最小值为 $-\frac{2}{13} \approx -0.1538$ 。
当 $\alpha_2 = 0$ 时：代入原式得 $4\alpha_1^2 - 2\alpha_1$ ，求偏导后得 $\alpha_1 = \frac{1}{4}$ ，再代入原式求最小值为 $-\frac{1}{4} = -0.25$ 。

最小值在 $(\frac{1}{4}, 0)$ 处取得，这是 SVM 对偶问题求解中处理约束条件、寻找最优解的关键推导流程。

6.求解每个 $\alpha$

$\alpha_1 = 1/4,\alpha_2 = 0$ ，由 $\boldsymbol{\alpha_3 = \alpha_1 + \alpha_2}$ ，得 $\boldsymbol{\alpha_3 = 1/4}$

7.求解参数 $\omega$

$\boldsymbol{\omega = \frac{1}{4} * 1 * (3,3) + \frac{1}{4} * (-1) * (1,1) = \left(\frac{1}{2},\frac{1}{2}\right)}$

8. 求解参数b

公式： $\boldsymbol{b = y_i - \omega\varPhi(x_i)}$

<1> 带入正例$y = 1$， $x(3,3)$ ： $\boldsymbol{b = 1 - \left(\frac{1}{2},\frac{1}{2}\right) \cdot (3,3) = 1 - \frac{6}{2} = -2}$
<2> 带入负例$y = -1$， $x(1,1)$ ： $\boldsymbol{b = -1 - \left(\frac{1}{2},\frac{1}{2}\right) \cdot (1,1) = -1 - 1 = -2}$

9.总方程

$\boldsymbol{\frac{1}{2}x_1 + \frac{1}{2}x_2 - 2 = 0}$

最后我们就求出svm的核函数为上图中的那条红线。

4.软间隔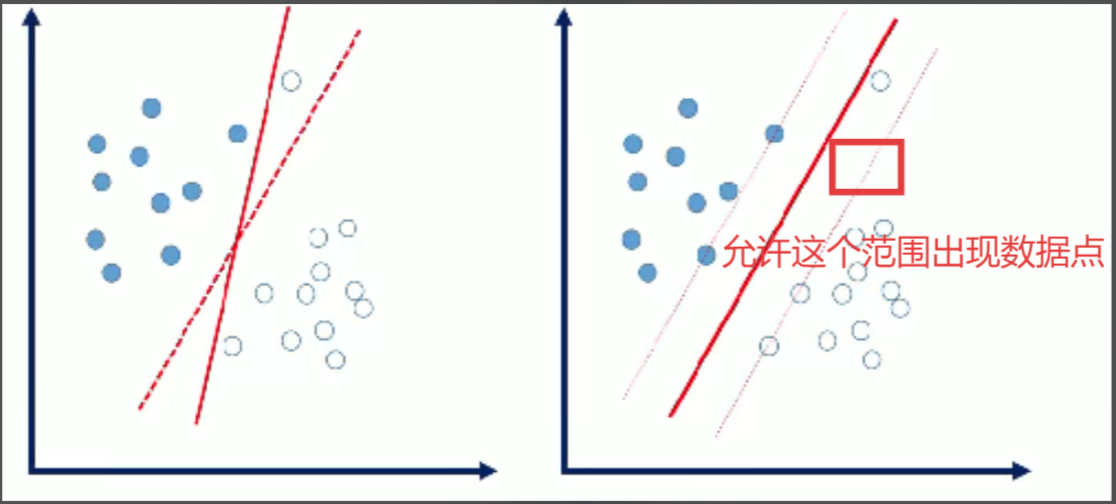

软间隔：数据中存在一些噪音点，如果考虑这些噪音点的话，超平面可能表现的效果不好。

我们允许个别样本点出现在间隔带里面。

量化指标：引入松弛因子。

原始： $\boldsymbol{y_i(\omega^t\varPhi(x_i) + b) \geq 1}$ [每个样本点必须满足]

放松： $\boldsymbol{y_i(\omega^t\varPhi(x_i) + b) \geq 1 - \xi_i}$ [个别样本点不用满足]

新的目标函数:
$\frac{1}{2}\|\omega\|^{2}+C \cdot \sum_{i = 1}^{n} \xi_{i}$
C：惩罚因子
(1) 当 C 值比较大时，说明分类比较严格，不容有误。

（2）当 C 值比较小时，说明分类比较宽松，可以有误。

三、核函数

谈一下核函数:
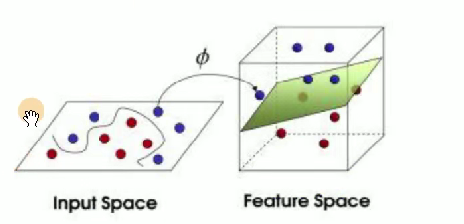
线性不可分情况:
在二维空间无法用一条直线分开，映射到三维 (或者更高维) 空间即可解决。
目标:
找到一个 $\boldsymbol{\varPhi(x_i)}$ ，对原始数据做一个变换。

1举例

假设有两个数据， $x1 = (x_1, x_2, x_3)$ ， $x2 = (y_1, y_2, y_3)$ ，如果数据在三维空间无法线性可分，我们通过核函数将其从三维空间映射到更高的九维空间，那么此时：

$f(x) = (x_1x_1, x_1x_2, x_1x_3, x_2x_1, x_2x_2, x_2x_3, x_3x_1, x_3x_2, x_3x_3)$

如果计算内积的话，x1与x2计算即 $<f(x1)·f(x2)>$ ，此时计算复杂度= 81，原始数据复杂度为$3*3 = 9$，那么对于映射到n维空间，复杂度为： $O(n^2)$

对于数据点：x1 = (1,2,3)，x2 = (4,5,6)，则f(x1) = (1,2,3,2,4,6,3,6,9)，f(x2) = (16,20,24,20,25,30,24,30,36)，此时计算<f(x1)·f(x2)>= 16 + 240 + 72 + 40 + 100 + 180 + 72 + 180 + 324 = 1024

一个巧合

$K(x,y) = (<x1, x2>)^2 = (4 + 10 + 18)^2 = 32^2 = 1024$