神经网络-local minima and saddle point

当损失函数（Loss）不再下降时

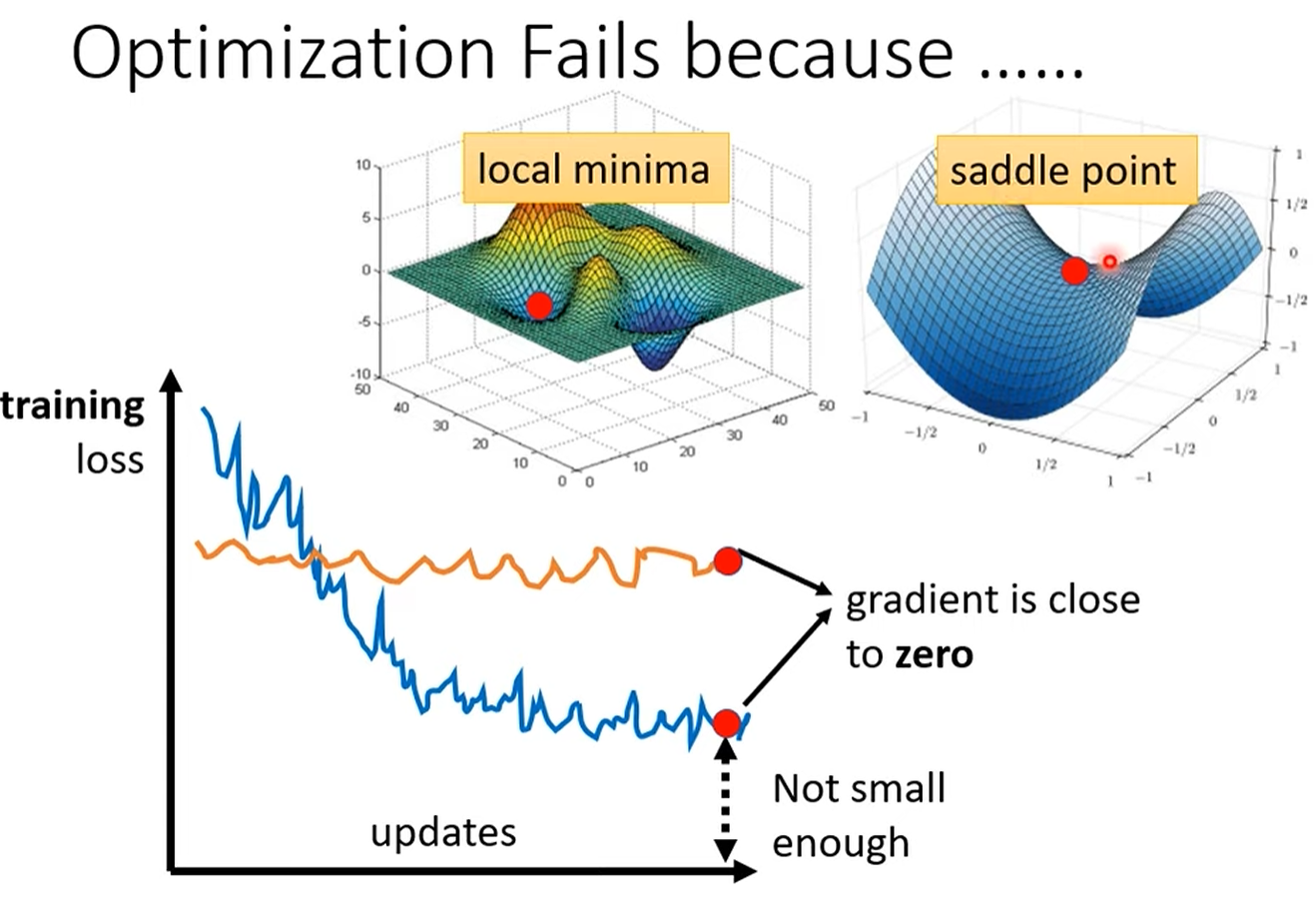
训练模型时最常遇到的问题：当损失函数（Loss）不再下降时，我们该怎么办？

通常，我们的第一反应是认为模型走到了一个“临界点”（Critical Point），比如局部最小值（Local Minima）或鞍点（Saddle Point），在这些点上梯度为零，模型无法再更新。

然而，老师指出，这其实是一种误解。在实际的高维复杂模型中，Loss不再下降，但梯度（Gradient）的模长（Norm）可能依然非常大。这意味着参数的更新步伐并没有停止，模型并非“卡”在一个点上。真正的原因更可能是在一个狭长的“山谷”地带，模型在谷底的两侧来回震荡，虽然每一步都在更新，但宏观上Loss值却无法有效下降

优化失败：不只是局部最小值

当模型训练停滞，梯度下降算法无法继续更新参数时，我们通常会假设梯度（Gradient）已经接近于零。梯度为零的点被称为“关键点”（Critical Point），它主要分为两类：

1. 局部最小值 (Local Minima)：这是一个大家都很熟悉的概念。当模型走到一个点，其周围所有方向的损失都比当前点高时，这个点就是局部最小值。此时，模型似乎无路可走。

2. 鞍点 (Saddle Point)：这是另一个梯度为零的点，但它的形状像一个马鞍。在某些方向上，损失会比当前点高，而在另一些方向上，损失会比当前点低。

泰勒展开近似

1. 展开公式

$$L(\theta )\approx L({\theta }^{\prime })+(\theta -{\theta }^{\prime }{)}^{T}g+\frac{1}{2}(\theta -{\theta }^{\prime }{)}^{T}H(\theta -{\theta }^{\prime })$$

• $L({\theta }^{\prime })$：蓝点的函数值（常数项）

• $(\theta -{\theta }^{\prime }{)}^{T}g$：绿色实线，一阶梯度项，切线近似

• $\frac{1}{2}(\theta -{\theta }^{\prime }{)}^{T}H(\theta -{\theta }^{\prime })$：红色二阶项，用曲率修正一阶近似的误差

2. 图中对应关系

• 蓝色点 ${\theta }^{\prime }$：展开点（已知值）

• 绿色实线：梯度一阶近似 $(\theta -{\theta }^{\prime }{)}^{T}g$，表示沿切线方向的预测变化量

• 红色曲线修正部分：二阶 Hessian 项，考虑曲率后得到更准确的近似

• 黑色曲线：真实函数 L(θ)

3. 几何含义

• 从蓝点到黑点的垂直高度 = 常数项 + 一阶项 + 二阶项

• 一阶项（绿色）= 变化率 × 位移（通过点乘得到）

• 二阶项（红色）= 曲率修正，使近似贴合真实曲线

数学角度判断critical point

saddle point 还可以下降

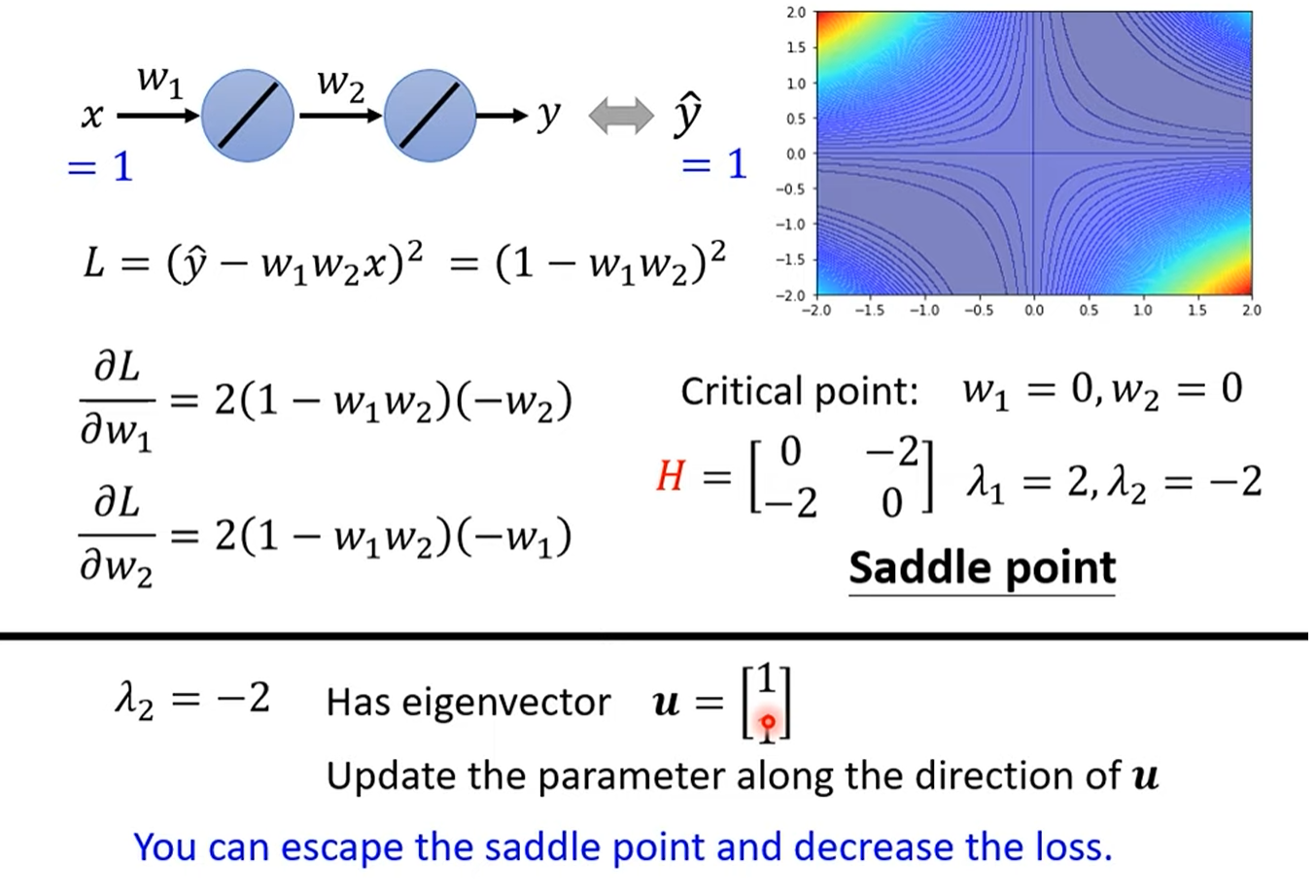
高维空间的普遍现象：鞍点远多于局部最小值

深度学习模型的参数动辄百万甚至上亿，其损失函数存在于一个极高的维度空间中。有研究表明，在这种高维空间里，真正的局部最小值其实非常罕见。我们训练时遇到的大多数梯度为零的关键点，实际上都是鞍点。实验证据也支持了这一假说：在模型训练停滞时，其对应的Hessian矩阵通常仍包含大量的负特征值，这意味着在许多维度上，仍然存在可以降低损失的路径。

Minimum ratio：

$$Minimumratio=\frac{正的特征值数量}{总特征值的数量}$$

这个比率可以看作是判断一个“critical point ”（梯度为零的点）究竟是局部最小值还是鞍点的一个量化指标。

让我们来深入解读一下这个比率的含义：

1. 当比率 = 1时：

   • 这意味着Hessian矩阵所有的特征值都是正数。

   • 根据我们之前的讨论，这正是局部最小值 (Local Minimum) 的明确数学定义。此时，无论你从哪个方向离开这个点，损失函数的值都会上升。

2. 当 0 < 比率 < 1时：

   • 这意味着Hessian矩阵的特征值中，既有正数也有负数。

   • 这就是鞍点 (Saddle Point) 的情况。这个比率告诉我们，存在一些方向（对应正特征值）可以让损失函数上升，同时也存在另一些方向（对应负特征值）可以让损失函数下降。

3. 当比率 = 0时：

   • 这意味着所有的特征值都是负数。

   • 这种情况对应的是局部最大值 (Local Maximum)，在损失函数优化中这通常不是我们关心的问题。