PCA多变量离群点检测:Hotelling‘s T2与SPE方法原理及应用指南
主成分分析(Principal Component Analysis, PCA)作为一种经典的无监督降维技术,在保留数据主要信息的同时能够有效压缩数据维度。由于PCA对数据变异性的高度敏感性,该方法在多变量异常值检测领域展现出独特的优势。
当分析任务需要建立早期预警系统以识别异常状态,并且要求结果具备良好的可解释性和透明度时,基于PCA的异常检测方法提供了理想的解决方案。尽管多变量数据集的异常值检测因高维性和无标签特性而面临诸多挑战,但PCA方法凭借其固有的降维能力和可视化特性,为这一难题提供了有效的解决途径。
本文将系统阐述基于PCA的异常值检测理论框架,重点介绍霍特林T²统计量和SPE/DmodX(平方预测误差/距离建模残差)两种核心方法,并通过连续变量和分类变量的实际案例,详细演示无监督异常值检测模型的构建过程。
异常值检测方法论:单变量与多变量分析的比较
异常值检测的方法学框架可以划分为单变量和多变量两种基本范式(图1)。单变量方法采用逐个变量分析的策略,通过数据分布特征分析来识别偏离正常范围的观测值,这种方法在处理低维数据时具有较好的效果。
多变量方法则同时考虑多个特征变量之间的相互关系,能够捕获线性或非线性关联模式中的异常观测,对于具有偏斜分布特征的高维数据表现出更强的检测能力。在Python生态系统中,scikit-learn库提供了丰富的多变量异常检测算法实现,包括单类支持向量机(One-Class SVM)、孤立森林(Isolation Forest)和局部异常因子(Local Outlier Factor)等方法。
本文专注于基于主成分分析的多变量异常值检测方法,该方法的核心优势在于其优异的可解释性:通过PCA的降维特性,异常值可以在低维空间中进行直观的可视化展示,为分析人员提供清晰的几何直觉。
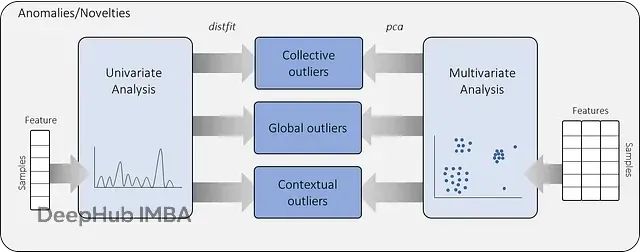
图1. 单变量与多变量异常值检测方法的分析框架比较。多变量数据集的异常值检测方法是本文的核心内容
异常值与新颖性检测的概念区分
在异常值检测的理论框架中,异常(Anomaly)和新颖性(Novelty)代表两种不同性质的偏离行为模式。异常值是指那些在历史数据中已有类似模式出现,但明显偏离正常分布的观测值,这类检测任务通常应用于欺诈识别、网络入侵检测和设备故障诊断等场景。
新颖性检测则关注于识别前所未见的数据模式,旨在发现新的行为模式或事件类型。在新颖性检测任务中,领域专业知识的融入显得尤为重要,因为需要准确判断新模式是否代表真正的异常情况还是合理的数据变化。
无论是异常值检测还是新颖性检测,其核心挑战都在于"正常"行为模式的定义往往具有主观性,并且会因具体应用场景而产生显著差异。这种定义的模糊性要求检测算法必须具备足够的鲁棒性和适应性。
PCA在异常值检测中的理论基础
主成分分析通过线性变换将原始数据投影到方差最大的方向上,从而实现数据的有效降维。PCA方法对于不同数值范围的变量具有天然的敏感性,这一特性使其在异常值检测任务中表现出色。该方法的主要优势包括:能够将高维数据映射到二维或三维空间进行可视化展示,便于研究人员直观验证检测结果;提供良好的变量可解释性,有助于理解异常值的成因;可与多种距离度量方法相结合,进一步提升检测精度。
本文采用的PCA库集成了两种主要的异常值检测方法:霍特林T²统计量和SPE/DmodX方法。霍特林T²统计量基于多元正态分布假设,通过计算观测值在主成分空间中到数据中心的马氏距离来识别异常值。SPE/DmodX方法则通过计算原始观测值与其在主成分空间中投影值之间的重构误差来检测异常模式。
连续变量异常值检测的实证分析
本节通过葡萄酒数据集的分析案例,详细演示霍特林T²和SPE/DmodX方法在连续变量异常值检测中的应用。该数据集来源于sklearn库,包含178个样本、13个理化特征变量和3个葡萄酒类别标签[4]。
# 安装pca库
pip install pca
# 加载必需的库
from sklearn.datasets import load_wine
import pandas as pd# 加载葡萄酒数据集
data = load_wine()# 构建数据框架
df = pd.DataFrame(index=data.target, data=data.data, columns=data.feature_names)print(df)
# alcohol malic_acid ash ... hue ..._wines proline
# 0 14.23 1.71 2.43 ... 1.04 3.92 1065.0
# 0 13.20 1.78 2.14 ... 1.05 3.40 1050.0
# 0 13.16 2.36 2.67 ... 1.03 3.17 1185.0
# 0 14.37 1.95 2.50 ... 0.86 3.45 1480.0
# 0 13.24 2.59 2.87 ... 1.04 2.93 735.0
# .. ... ... ... ... ... ...
# 2 13.71 5.65 2.45 ... 0.64 1.74 740.0
# 2 13.40 3.91 2.48 ... 0.70 1.56 750.0
# 2 13.27 4.28 2.26 ... 0.59 1.56 835.0
# 2 13.17 2.59 2.37 ... 0.60 1.62 840.0
# 2 14.13 4.10 2.74 ... 0.61 1.60 560.0
# # [178 rows x 13 columns]
数据集的初步分析表明各特征变量的数值范围存在显著差异。例如,灰分(ash)含量的数值集中在2附近,而脯氨酸(proline)含量则达到1000以上的量级。这种量纲差异要求在分析前进行标准化处理,以确保各变量对主成分的贡献不会因数值范围的差异而产生偏倚。
PCA库提供了内置的数据标准化功能,通过设置
normalize=True
参数即可实现零均值单位方差的标准化处理。在模型初始化阶段,可以通过
detect_outliers
参数同时指定霍特林T²(
ht2
)和SPE/DmodX(
spe
)两种异常值检测方法。
# 导入PCA库
from pca import pca# 初始化PCA模型并配置异常值检测方法
model = pca(normalize=True, detect_outliers=['ht2', 'spe'], n_std=2)# 执行模型拟合和数据变换results = model.fit_transform(df)
模型拟合完成后,PCA库会为每个样本计算异常值评分。输出结果包含多个统计指标:前四列(
y_proba
、
p_raw
、
y_score
、
y_bool
)对应霍特林T²方法的检测结果,后两列(
y_bool_spe
、
y_score_spe
)则基于SPE/DmodX方法计算得出。
霍特林T²统计量通过对前
n_components
个主成分进行卡方检验并计算相应的p值,实现异常值的强弱排序,其中
y_proba
值越小表示异常程度越高。该方法的检测范围限定在PC1到PC5维度内,基于主要方差(以及潜在的异常值)通常集中在前几个主成分的经验假设。当前五个主成分无法充分捕获数据方差时,可以适当增加检测维度的深度。
# 绘制霍特林T²方法的异常值检测结果
model.biplot(SPE=False, HT2=True, density=True, marker=data.target, s=df['malic_acid']*100, title='基于霍特林T²统计量的异常值标识')# 生成三维可视化图
model.biplot3d(SPE=False, HT2=True, density=True, arrowdict={'scale_factor': 2.5, 'fontsize': 20}, title='基于霍特林T²统计量的异常值标识')# 提取SPE/DmodX方法识别的异常值df.loc[results['outliers']['y_bool'], :]
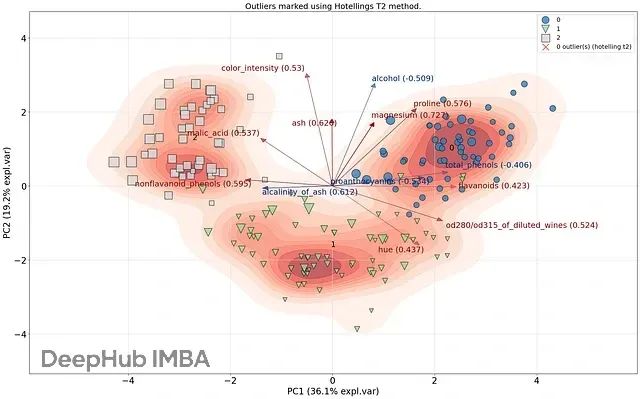
图2A. 主成分PC1与PC2的散点分布及样本投影。霍特林T²方法在此数据集中未检测到异常值。
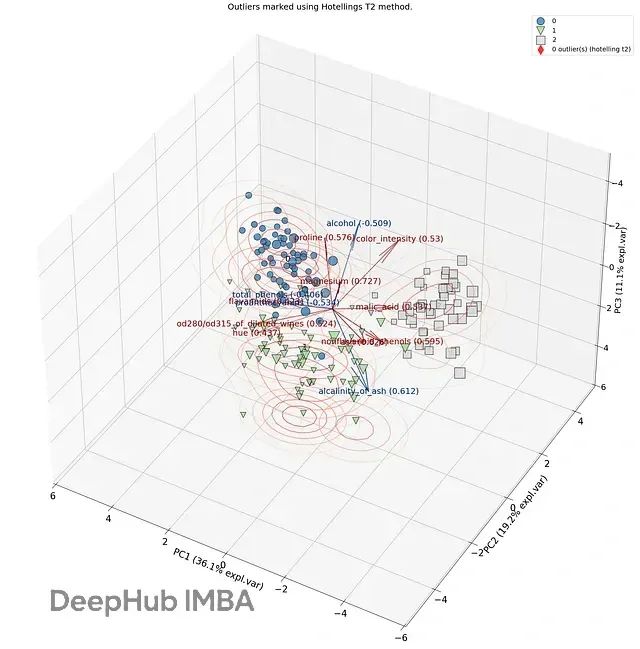
图2B. 三维主成分空间中的样本分布,未发现明显的异常值模式。
SPE/DmodX方法通过计算原始观测值与其在主成分空间中投影值之间的欧几里得距离来量化重构误差。该方法中,到数据中心的距离由霍特林T²值表征,因此图3中的椭圆边界代表基于霍特林T²统计量的异常值判定阈值。
当样本点位于椭圆边界外部时,即被判定为异常值。这一判定准则基于前两个主成分的均值和协方差矩阵计算得出(图3)。通过SPE/DmodX方法,本案例共检测并标记了11个异常值样本。
# 绘制SPE/DmodX方法的异常值检测结果
model.biplot(SPE=True, HT2=False, density=True, marker=data.target, s=df['malic_acid']*100, title='基于SPE/DmodX方法的异常值标识')# 生成三维可视化图
model.biplot3d(SPE=True, HT2=False, density=True, marker=data.target, s=df['malic_acid']*100, title='基于SPE/DmodX方法的异常值标识')# 提取SPE/DmodX方法识别的异常值df.loc[results['outliers']['y_bool_spe'], :]
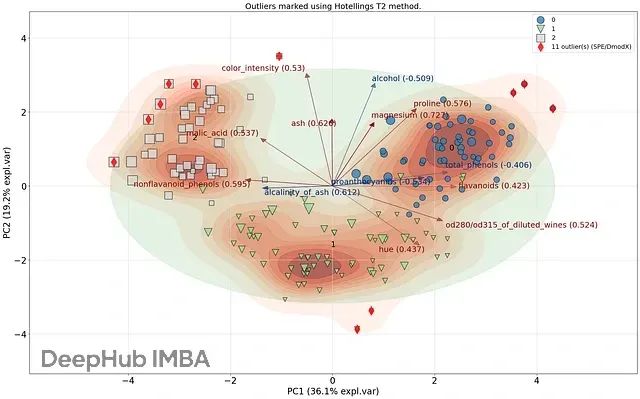
图3A. 异常值检测结果的综合展示:菱形标记表示SPE/DmodX方法检测的异常值,叉号标记表示霍特林T²方法检测的异常值。
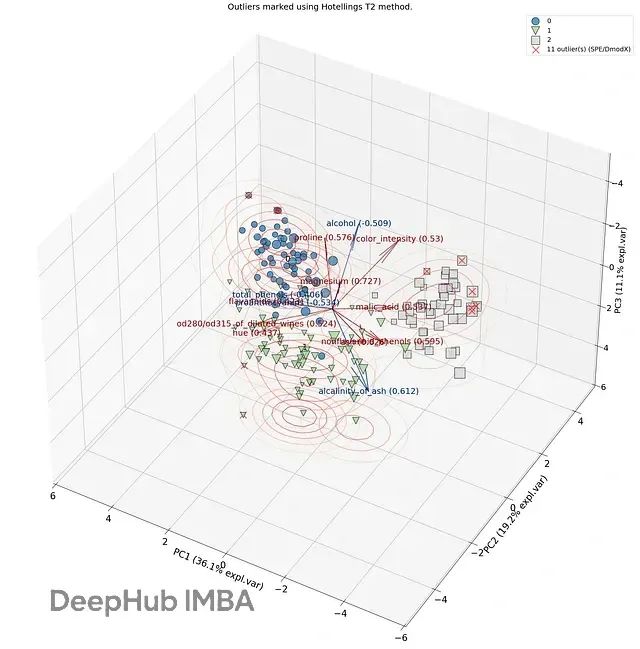
图3B. SPE/DmodX方法检测异常值的三维空间可视化结果。
两种方法的结果对比分析可以通过计算重叠异常值来实现。尽管在本案例中霍特林T²检验未检测到异常值,但通过逻辑运算仍可以直接计算两种方法的一致性区域。
# 计算两种方法检测结果的重叠区域
I_overlap = np.logical_and(results['outliers']['y_bool'], results['outliers']['y_bool_spe'])# 输出重叠异常值
df.loc[I_overlap, :]## 分类变量异常值检测的方法与实现分类变量的异常值检测面临着距离度量标准化的技术挑战。由于分类变量缺乏自然的数值排序关系,必须通过适当的编码方法将其转换为数值形式,并确保变量间距离的可比性。独热编码(One-Hot Encoding)作为处理分类变量的标准方法,能够将每个分类水平转换为二进制向量表示,从而为后续的PCA分析奠定基础。经过独热编码处理的数据集可以直接应用霍特林T²和SPE/DmodX方法进行异常值检测。本节采用学生成绩数据集[5]作为分析案例,该数据集包含649个样本和33个变量,涵盖了学生的人口统计学特征、家庭背景、学习习惯等多个维度的信息。在数据预处理阶段,需要对所有分类变量进行审查。对于标识符变量或连续型浮点变量,应根据分析需求进行删除或离散化处理,以确保数据集的一致性和分析结果的有效性。```python
# 导入PCA库
from pca import pca# 初始化PCA模型
model = pca()# 加载学生成绩数据集
df = model.import_example(data='student')print(df)
# school sex age address famsize Pstatus ... Walc health absences
# 0 GP F 18 U GT3 A ... 1 3 4
# 1 GP F 17 U GT3 T ... 1 3 2
# 2 GP F 15 U LE3 T ... 3 3 6
# 3 GP F 15 U GT3 T ... 1 5 0
# 4 GP F 16 U GT3 T ... 2 5 0
# .. ... .. ... ... ... ... ... ... ... ...
# 644 MS F 19 R GT3 T ... 2 5 4
# 645 MS F 18 U LE3 T ... 1 1 4
# 646 MS F 18 U GT3 T ... 1 5 6
# 647 MS M 17 U LE3 T ... 4 2 6
# 648 MS M 18 R LE3 T ... 4 5 4 # [649 rows x 33 columns]
独热编码的实施是分类变量异常值检测的关键步骤。该过程将原始的分类变量转换为多个二进制虚拟变量,使得不同类别之间的距离计算变得可行且有意义。对于本案例的649个样本和33个原始变量,独热编码后的数据维度扩展至177列,为后续的PCA分析提供了合适的数值输入。
# 安装独热编码库
pip install df2onehot
# 导入独热编码库
from df2onehot import df2onehot# 执行独热编码变换
df_hot = df2onehot(df)['onehot']print(df_hot)
# school_GP school_MS sex_F sex_M ...
# 0 True False True False ...
# 1 True False True False ...
# 2 True False True False ...
# 3 True False True False ...
# 4 True False True False ...
# .. ... ... ... ... ...
# 644 False True True False ...
# 645 False True True False ...
# 646 False True True False ...
# 647 False True False True ...
# 648 False True False True ... # [649 rows x 177 columns]
经过独热编码处理的数据集现在可以作为PCA模型的输入进行异常值检测。在模型配置阶段,除了启用数据标准化功能(
normalize=True
)外,还需要适当调整统计参数以适应高维分类数据的特点。本案例中设置显著性水平
alpha=0.05
,标准差倍数
n_std=3
,并采用FDR-BH方法进行多重比较校正,以控制假发现率。
# 配置PCA模型参数
model = pca(normalize=True,detect_outliers=['ht2', 'spe'],alpha=0.05,n_std=3,multipletests='fdr_bh')# 执行模型拟合和变换
results = model.fit_transform(df_hot)
# [649 rows x 177 columns]
# [pca] >Processing dataframe..
# [pca] >Normalizing input data per feature (zero mean and unit variance)..
# [pca] >The PCA reduction is performed to capture [95.0%] explained variance using the [177] columns of the input data.
# [pca] >Fit using PCA.
# [pca] >Compute loadings and PCs.
# [pca] >Compute explained variance.
# [pca] >Number of components is [116] that covers the [95.00%] explained variance.
# [pca] >The PCA reduction is performed on the [177] columns of the input dataframe.
# [pca] >Fit using PCA.
# [pca] >Compute loadings and PCs.
# [pca] >Outlier detection using Hotelling T2 test with alpha=[0.05] and n_components=[116]
# [pca] >Multiple test correction applied for Hotelling T2 test: [fdr_bh]
# [pca] >Outlier detection using SPE/DmodX with n_std=[3]
# [pca] >Plot PC1 vs PC2 with loadings.# 识别两种方法的重叠异常值
overlapping_outliers = np.logical_and(results['outliers']['y_bool'],results['outliers']['y_bool_spe'])
# 展示重叠异常值的详细信息
df.loc[overlapping_outliers]
# school sex age address famsize Pstatus ... Walc health absences
# 279 GP M 22 U GT3 T ... 5 1 12
# 284 GP M 18 U GT3 T ... 5 5 4
# 523 MS M 18 U LE3 T ... 5 5 2
# 605 MS F 19 U GT3 T ... 3 2 0
# 610 MS F 19 R GT3 A ... 4 1 0 # [5 rows x 33 columns]
分析结果表明,霍特林T²检验识别出85个异常值样本,而SPE/DmodX方法检测到6个异常值(详见图4图例说明)。两种方法的重叠检测结果包含5个样本,这些样本在主成分空间中表现出明显偏离主体分布的特征。通过
biplot
功能可以实现结果的可视化展示,并根据特定分类变量(如性别标签)对样本进行颜色编码,以支持更深入的模式分析。
异常值在图中分别以
x
和
*
符号进行标记。这种可视化表示为深度分析提供了有效的起点。从图4可以观察到,5个重叠异常值明显偏离了主体样本的分布模式,值得进一步调查。
对于异常值的排序和分析,可以利用霍特林T²方法的
y_proba
值(数值越小异常程度越高)和SPE/DmodX方法的
y_score_spe
值(该值表示样本到数据中心的欧几里得距离,数值越大异常程度越高)。此外,通过分析主成分载荷矩阵,可以深入理解这些异常学生样本的具体特征模式。
# 生成综合双标图进行结果可视化
model.biplot(SPE=True,HT2=True,n_feat=10,legend=True,labels=df['sex'],marker=df['sex'],title='学生成绩数据集异常值检测结果',figsize=(25, 15),color_arrow='k',arrowdict={'fontsize':16, 'c':'k'},cmap='bwr',gradient='#FFFFFF',edgecolor=None,density=True,s=df['absences']*25,)
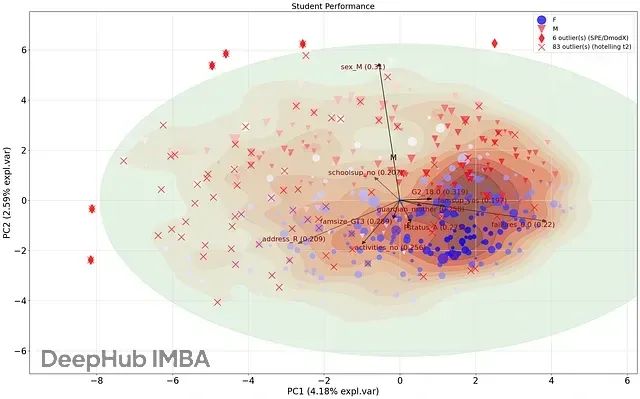
图4. 分类变量异常值检测的综合结果展示:菱形标记表示SPE/DmodX方法检测的异常值,叉号标记表示霍特林T²方法检测的异常值。
结论
本文系统展示了基于主成分分析的多变量异常值检测方法在连续变量和分类变量场景中的理论原理与实践应用。通过PCA库集成的霍特林T²统计量和SPE/DmodX方法,研究人员能够有效识别和量化多变量数据集中的异常观测值。
该方法框架的核心优势体现在其优秀的可解释性:通过主成分载荷的分析,可以深入理解各个变量对异常模式的贡献程度;借助双标图在低维主成分空间中的可视化功能,能够直观展示异常值的分布特征和偏离程度。这种视觉化的分析能力为研究人员提供了关于异常值检测结果的直观理解,并为后续的深入分析和决策制定提供了有力支撑。
在实际应用中,异常值检测始终面临着"正常"行为模式定义的主观性挑战。不同应用领域对于异常值的判定标准可能存在显著差异,这要求分析人员在使用这些技术方法时,必须结合具体的业务背景和领域专业知识,以确保检测结果的实用性和可操作性。随着数据科学技术的不断发展,基于PCA的异常值检测方法将在更广泛的应用场景中发挥重要作用。
https://avoid.overfit.cn/post/8c6580ce36cc43dbaba5ddacbc915bad
作者:Erdogan T
