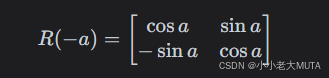位置编码——RoPE篇

前言

在自注意力机制中，注意力得分通过  计算得出，其中：

• Q：查询向量，表示当前词与其他词的关系；
• K：键向量，用于表示其他词的特征；
• 标准点积 q⋅k 直接衡量两个向量之间的相似性。

在 Transformer 模型中，位置编码通过向输入的词向量中加入或结合位置信息，使得模型感知序列中词语的顺序关系。

RoPE 的核心技术是通过一个旋转变换，将位置信息嵌入到词向量的每个维度中，从而实现位置关系的建模。主要特点包括：

1. 旋转变换：将序列中每个位置的向量，通过应用一个与位置相关的二维旋转变换来编码。
2. 相对位置关系建模：RoPE 的设计使得输入向量经过注意力机制时，其点积结果中自然隐含了相对位置的信息。

---

二维向量旋转

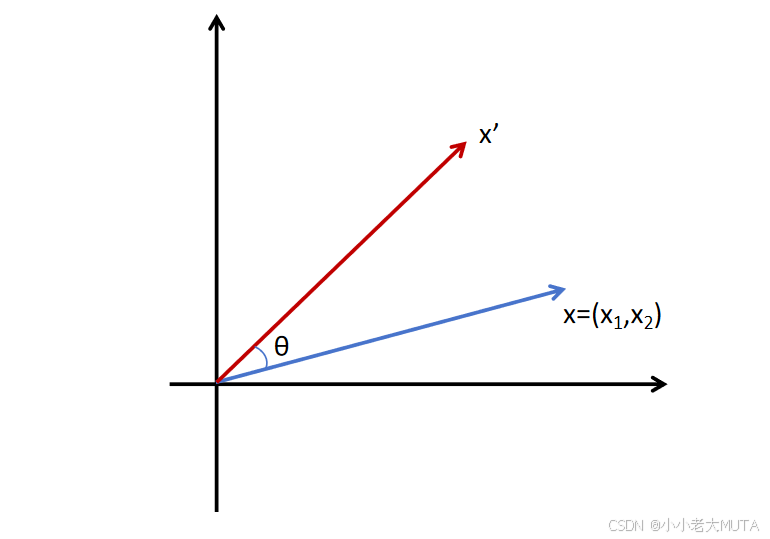
假设二维向量为 x=(x1,x2)，我们可以通过一个旋转矩阵对其进行位置编码。旋转矩阵形式为：

将旋转矩阵应用于 x 后，得到旋转后的向量：

这个操作的几何意义是：将原向量绕原点旋转一个角度 θ，从而引入位置信息。

旋转矩阵性质

（1）

（2） 

证明：

（1）

三角函数的和角公式如下：

得：

（2）

三角函数性质如下：

得：

---

引入旋转位置编码的注意力点积

在自注意力机制中，给定输入序列，假设其查询向量 q、键向量 k 都经过 RoPE 编码，分别对应于位置 p 和 q。带有位置编码的向量表示为：

 

其中：

是旋转矩阵，旋转角度是;

,是与维度相关的频率缩放因子。

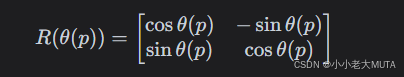
点积变成了：

因为，所以：

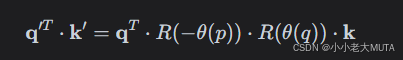
又因为，所以：

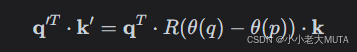
这里的  是一个仅与相对位置 q−p相关的旋转矩阵，这表明 RoPE 的点积自然地反映了两个位置之间的相对位置信息。

---

几何解释

1. 每个向量 q 和 k 都被映射到位置敏感的旋转空间中。
2. 在点积计算中，旋转矩阵会相对调整向量的方向，使得点积结果包含两词之间的相对位置关系。
3. 这意味着，注意力机制中的点积不仅仅衡量两词的内容相似性，还显式地编码了它们之间的相对位置信息。

---

多维向量

参考：位置编码有什么用？简单讲解位置编码原理 + 源码解读（绝对 / 相对 / RoPE）_哔哩哔哩_bilibili

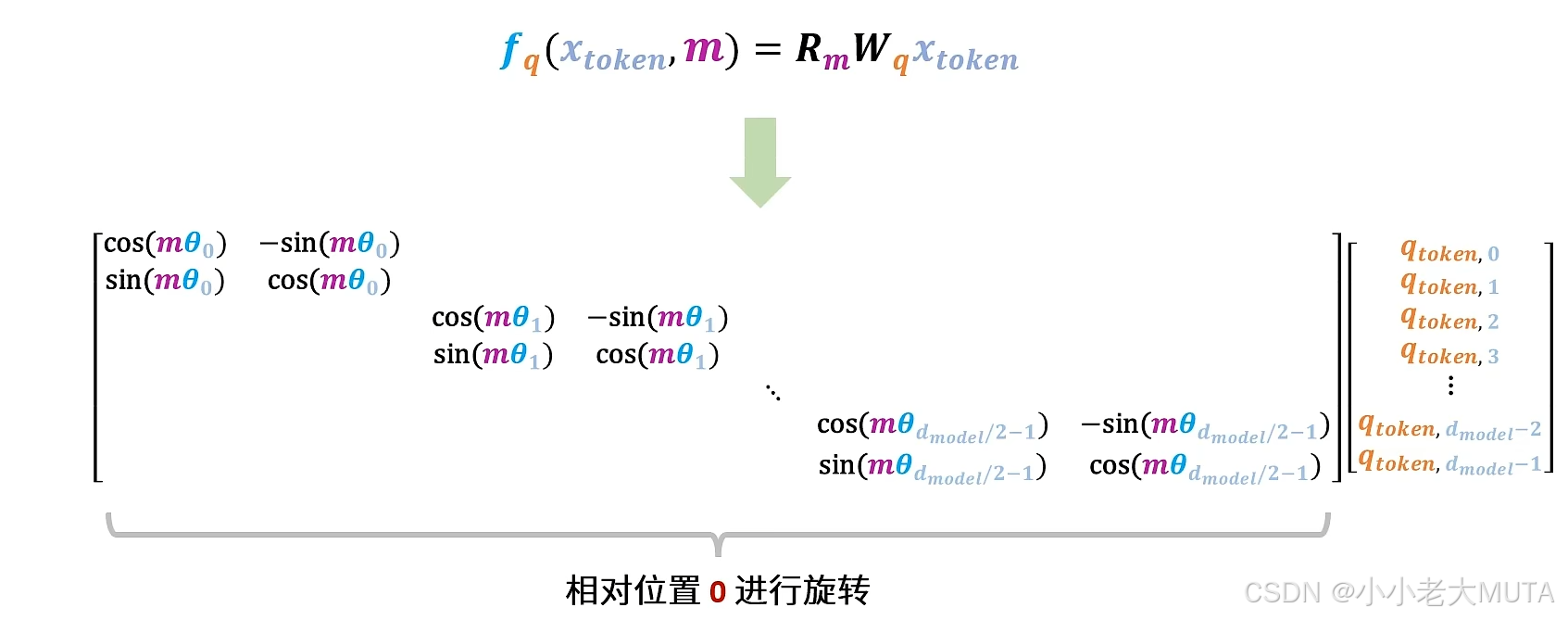
高效的等价方法：