哈希表——指针数组与单向链表的结合

哈希表（散列表） 深度拆解

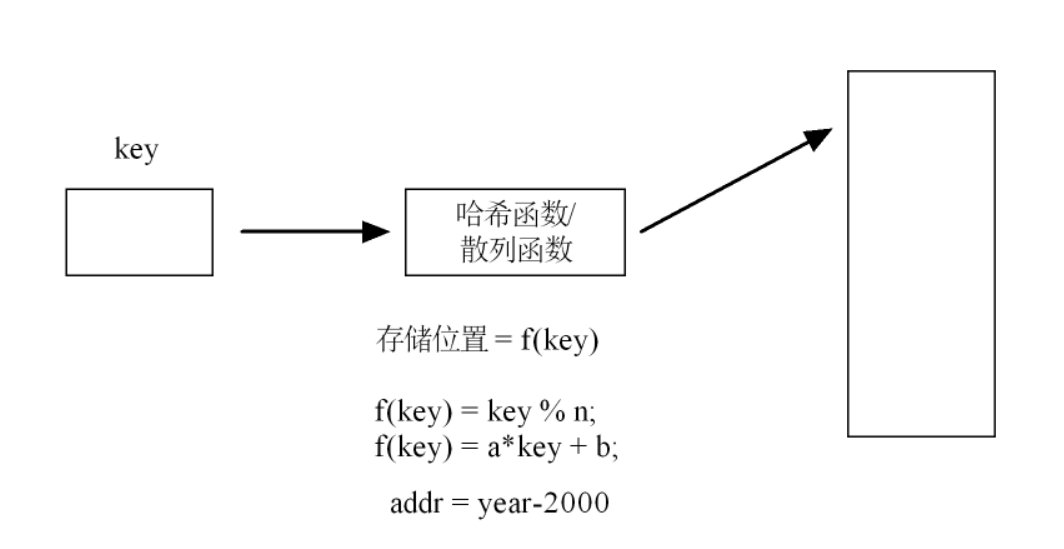
1. 哈希表的“高效查找”本质

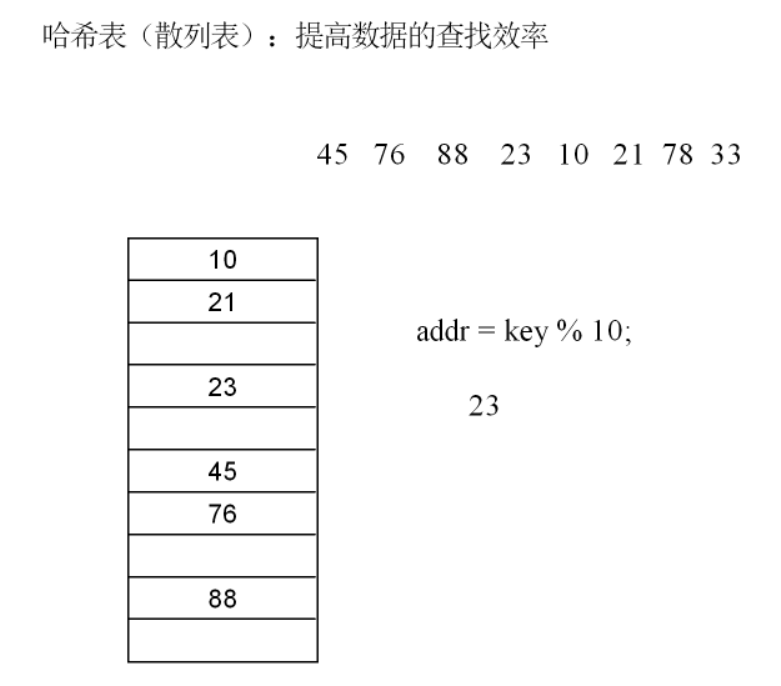
哈希表能快速查找，核心是跳过“遍历比较” 。比如找关键字 key=45 ，不用从数组头遍历找，而是用 addr = key % 10 直接算出它该存在下标 5（假设 key=45 ，45%10=5 ），直接去下标 5 找数据，一步到位，这就是哈希表平均时间复杂度接近 O(1) 的原因。

2. 哈希函数的“设计门道”

笔记里提到了两种哈希函数：

• 除留余数法（f(key) = key % n ）：
  选 n 很关键！如果选合数（比如 n=10 ，但 10 是合数），关键字是 10、20、30 这类数时，key%10 结果都是 0 ，冲突概率会很高。所以实际开发中，n 一般选质数（比如 7、11、13 等 ），让关键字分布更均匀，减少冲突。
  

• 直接定址法（f(key) = a*key + b ）：
  适合关键字本身是连续、均匀分布的场景。比如关键字是“员工工号”，工号是 1001、1002、1003... ，用 a=1, b=0 ，直接 f(key)=key ，把工号当数组下标，查找时直接定位，效率极高。
  除了笔记中提到的除留余数法、直接定址法，哈希函数还有以下几种常见类型：

补充：

1. 数字分析法

原理：当关键字是位数较多的数字时，分析关键字中每位数字的分布情况，选择分布均匀的若干位组成哈希地址。例如，有一组关键字是由年份、月份、日期和流水号组成的 10 位整数，形如 YYYYMMDDNN（YYYY 代表年份，MM 代表月份，DD 代表日期，NN 代表流水号）。经过分析发现，年份和月份部分的数字分布不均匀（如年份基本集中在某几个连续区间内），而流水号部分的数字分布较为均匀，就可以选取流水号部分的数字作为哈希地址，或者对流水号进行适当的运算后得到哈希地址。
适用场景：适用于关键字位数较多，且其中某些位上的数字分布不均匀的情况，能有效减少哈希冲突。

2. 折叠法

原理：将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后把这几部分叠加求和，并按照哈希表的表长，取后几位作为哈希地址。折叠法又分为移位叠加和间界叠加。
- 移位叠加：把分割后的每一部分低位对齐相加。例如，关键字为 1234567890，若哈希表长度为 3 位，将其分割成 123、456、789 和 0 这几部分，移位叠加得到 123 + 456 + 789 + 0 = 1368，取后 3 位 368 作为哈希地址。
- 间界叠加：从一端向另一端沿分割界来回折叠后对齐相加。比如还是上述关键字，间界折叠后得到 123、654（456 折叠）、789 和 0，相加 123 + 654 + 789 + 0 = 1566，取后 3 位 566 作为哈希地址。
适用场景：当关键字的位数较多，且分布没有明显规律时，折叠法可以将关键字的各位数字充分利用起来，产生较为均匀的哈希地址。

3. 随机数法

原理：选择一个随机函数，以关键字作为随机函数的输入，随机函数的输出值作为哈希地址。例如，使用一个简单的伪随机函数 rand(key)，其中 key 是关键字，函数根据特定的随机算法返回一个在哈希表长度范围内的整数作为哈希地址。
适用场景：适用于关键字的取值范围不固定，且没有明显的数字分布特征的情况。不过由于随机函数本身的不确定性，在实际应用中需要注意哈希冲突的处理，通常会结合其他冲突解决方法一起使用。

4. 平方取中法

原理：先对关键字进行平方运算，然后取结果的中间若干位作为哈希地址。例如，关键字为 42，对其平方得到 42×42 = 1764，若哈希表长度为 3 位，可取中间的 76 作为哈希地址。之所以取中间位，是因为关键字平方后，其高位和低位的数字受原关键字的某些特征影响较大，分布可能不均匀，而中间位相对来说能更均匀地反映关键字的特征。
适用场景：当关键字的取值范围较小，且没有明显的数字分布规律时，平方取中法可以通过扩大关键字的取值范围并提取中间位，得到相对均匀分布的哈希地址，从而减少哈希冲突。

不同的哈希函数适用于不同特点的关键字集合，在实际应用中，需要根据关键字的特征、哈希表的大小以及对哈希冲突的容忍程度等因素，综合选择合适的哈希函数 。

3. 哈希冲突的“解决逻辑”

冲突场景：比如 key=15 和 key=25 ，用 addr = key%10 计算，结果都是 5 ，这两个关键字要存在同一个下标位置，就会冲突。

解决办法：

• 开放地址法（笔记里的“开放地址法”）：
  冲突时，按规则找下一个空位置。比如线性探测：如果下标 5 被占了，就依次往后找 6、7、8... ，直到找到空位置存数据。但这种方法有“聚集问题”—— 连续被占的下标会越来越多，影响效率。
• 链地址法（拉链法）（笔记里的“哈希表存链表首地址”）：
  哈希表的每个下标位置，存一个链表的头指针。冲突时，把数据挂到同一个链表上。比如 key=15 和 key=25 都算到下标 5 ，就把它们存在下标 5 对应的链表节点里。查找时，先定位到下标 5 ，再遍历链表找对应关键字，这种方法冲突处理更灵活，不会像开放地址法那样产生“聚集”。

4. 哈希表 vs 二分查找（场景对比）

• 二分查找：
  必须基于有序数组，每次缩小一半范围查找，时间复杂度 O(log₂n) 。但插入、删除数据时，要移动大量元素（保持数组有序），适合静态数据（数据插入删除少，主要查）。
• 哈希表：
  插入、查找平均复杂度接近 O(1) ，适合动态数据（频繁插入、删除、查找）。但要处理哈希冲突，而且如果哈希函数设计不好，冲突多了，效率会下降（比如链地址法里链表太长，查找要遍历链表，复杂度接近 O(n) ）。

知识串联 + 实际应用场景

• 循环队列：适合“按顺序排队处理”的场景，比如操作系统里的“任务队列”，多个任务按顺序入队、出队，用循环队列能高效利用内存，避免假溢出导致的资源浪费。
• 哈希表：适合“快速查询”的场景，比如“字典查询”（根据单词快速找释义 ）、“用户信息检索”（根据用户 ID 快速查资料 ），利用哈希函数直接定位，比遍历查找快很多。

课堂代码

头文件部分：

#ifndef __HASH_H__
#define __HASH_H__#define HASH_TABLE_MAX_SIZE 27   //宏定义哈希表指针数组的长度typedef struct per        //定义数据：
{char name[32];char tel[32];
}Data_type_t;typedef struct node    //定义结点：
{Data_type_t data;struct node *pnext;
}HSNode_t;extern int insert_hash_table(HSNode_t **hash_table, Data_type_t data);
extern void hash_for_each(HSNode_t **hash_table);
extern HSNode_t *find_hash_table(HSNode_t **hash_table, char *name);extern void destroy_hash_table(HSNode_t **hash_table);#endif

函数部分：

#include "hash.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>//根据姓名首字母来分组存储：
int hash_function(char key)
{if (key >= 'a' && key <= 'z'){return key-'a';}else if (key >= 'A' && key <= 'Z'){return key-'A';}else{return HASH_TABLE_MAX_SIZE-1;}
}int insert_hash_table(HSNode_t **hash_table, Data_type_t data)
{int addr = hash_function(data.name[0]);//申请结点保存数据//头插//hash_table[addr];   //---->pheadHSNode_t *pnode = malloc(sizeof(HSNode_t));if (NULL == pnode){printf("malloc error\n");return -1;}pnode->data = data;pnode->pnext = NULL;if (NULL == hash_table[addr]){hash_table[addr] = pnode;}else{if (strcmp(pnode->data.name, hash_table[addr]->data.name) <= 0){pnode->pnext = hash_table[addr];hash_table[addr] = pnode;}else{HSNode_t *p = hash_table[addr];while (p->pnext != NULL && (p->pnext->data.name, pnode->data.name) < 0)   //排序插入，！！！！！！！！！！{p = p->pnext;}pnode->pnext = p->pnext;p->pnext = pnode;}}return 0;
}void hash_for_each(HSNode_t **hash_table)
{for (int i = 0; i < HASH_TABLE_MAX_SIZE; ++i){HSNode_t *ptmp = hash_table[i];while (ptmp){printf("%s : %s\n", ptmp->data.name, ptmp->data.tel);ptmp = ptmp->pnext;}printf("\n");}
}HSNode_t *find_hash_table(HSNode_t **hash_table, char *name)
{int addr = hash_function(name[0]);HSNode_t *ptmp = hash_table[addr];while (ptmp){if (0 == strncmp(ptmp->data.name, name, strlen(name))){return ptmp;}ptmp = ptmp->pnext;}return NULL;
}void destroy_hash_table(HSNode_t **hash_table)
{for (int i = 0;i < HASH_TABLE_MAX_SIZE; i++){HSNode_t *pdel = hash_table[i];while (hash_table[i] != NULL){hash_table[i] = pdel->pnext;free(pdel);pdel = hash_table[i];}}
}

## 主函数部分：
#include <stdio.h>
#include "hash.h"int main(void)
{Data_type_t pers[5] = {{"zhangsan", "110"}, {"lisi", "120"},{"wanger", "119"}, {"Zhaowu", "122"},{"maliu", "10086"}};HSNode_t *hash_table[HASH_TABLE_MAX_SIZE] = {NULL};insert_hash_table(hash_table, pers[0]);insert_hash_table(hash_table, pers[1]);insert_hash_table(hash_table, pers[2]);insert_hash_table(hash_table, pers[3]);insert_hash_table(hash_table, pers[4]);hash_for_each(hash_table);HSNode_t *pnode = find_hash_table(hash_table, "zhang");if (pnode != NULL){printf("find : %s : %s\n", pnode->data.name, pnode->data.tel);}destroy_hash_table(hash_table);return 0;
}