当前位置： 首页 > news >正文

周志华院士西瓜书实战（三）聚类+邻居+PCA+特征选择+半监督学习

news 2025/8/8 16:20:09

一些sklearn的库的使用：

1. 半监督学习： SelfTrainingClassifier、Label Propagation

2. 特征选择与稀疏学习：

sklearn.feature_selection中 过滤式选择SelectKBest, chi2

                                            包裹式选择SelectFromModel

sklearn.linear_model 中的正则化回归 Lasso, Ridge

3. 聚类：

sklearn.cluster 中的 KMeans 和 DBSCAN

sklearn.mixture 中的 GaussianMixture

4. sklearn.neighbors 中的（KNN） KNeighborsClassifier

5. PCA 以及sparse版本 kernel版本

目录

1. 半监督学习

1.1 SelfTrainingClassifier 自监督训练分类

1.2 Label Propagation 标签传播

 2. 特征选择与稀疏学习

2.1 过滤式选择特征   挑k个特征

2.2 包裹式选择   确定模型后选择

2.3 嵌入式选择与L1正则化

3. 聚类

3.1 K-means

3.2 DBSCAN

3.3 GMM 高斯混合聚类

4. sklearn.neighbors 邻居算法

4.1 找最近的邻居

4.2 KNN 最近k个邻居投票

5. PCA 主成分分析

1. 半监督学习

周志华《机器学习导论》第13章 半监督学习-CSDN博客

 下例为 先对digits数据中 0~9 每个类别只选 10%的数据保留（模拟少量标记数据情形）

from sklearn.datasets import load_digits
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import numpy as np# 加载数据
X, y = load_digits(return_X_y=True)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分训练集和测试集（保持类别比例）
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42, stratify=y)# 创建未标注数据（更合理的生成方式）
def create_unlabeled_data(y, unlabeled_ratio=0.9, random_state=42):#每个类别中的0.9 标记为未标注样本np.random.seed(random_state)unlabeled_mask = np.zeros(len(y), dtype=bool)for class_label in np.unique(y):class_indices = np.where(y == class_label)[0]n_unlabeled = int(unlabeled_ratio * len(class_indices))unlabeled_mask[np.random.choice(class_indices, n_unlabeled, replace=False)] = Truereturn unlabeled_maskunlabeled_mask = create_unlabeled_data(y_train, unlabeled_ratio=0.9)
y_train_semi = y_train.copy()
y_train_semi[unlabeled_mask] = -1  # 标记未标注样本print(f"标注样本数: {sum(y_train_semi != -1)}")
print(f"未标注样本数: {sum(y_train_semi == -1)}")

1.1 SelfTrainingClassifier 自监督训练分类

在基础模型的基础上 加上SelfTrainingClassifier 进行数据标注 重新训练模型


SVC（支持向量分类）外套着SelfTrainingClassifier； 不断增添伪标记

from sklearn.semi_supervised import SelfTrainingClassifier
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, classification_report# 创建并训练自训练分类器
base_svm = SVC(kernel='rbf',probability=True,  # 必须支持概率预测class_weight='balanced',  # 处理可能的类别不平衡random_state=42
)self_training = SelfTrainingClassifier(base_svm,threshold=0.75,  # 高置信度阈值，减少错误传播criterion='threshold',max_iter=50,verbose=True  # 显示训练过程
)self_training.fit(X_train, y_train_semi)# 评估模型
y_pred = self_training.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("\n测试集准确率: {:.4f}".format(accuracy))
print(classification_report(y_test, y_pred))# 查看自训练过程信息
print("\n自训练过程统计:")
print(f"最终迭代次数: {self_training.n_iter_}")
print(f"终止条件: {self_training.termination_condition_}")
print(f"新增伪标签样本数: {sum(self_training.labeled_iter_ > 0)}")

1.2 Label Propagation 标签传播

（1）构建数据样本之间的相似图

RBF核：生成全连接图（密集矩阵）           KNN核：生成稀疏图（仅保留k个最近邻连接）

（2）标签传播过程

LabelPropagation：完全信任初始标签（alpha=1）

LabelSpreading：多一个参数 通过alpha控制标签可信度（默认0.8表示保留80%初始标签权重）

from sklearn.semi_supervised import LabelSpreading
from sklearn.metrics import accuracy_score, classification_report
label_spread = LabelSpreading(kernel='knn',    # 使用K近邻构建相似图（比RBF更适合数字数据）n_neighbors=7,   # 增加近邻数提高稳定性alpha=0.8,       # 标签保留强度（0.8=80%信任原始标签）max_iter=30,     # 增加迭代次数确保收敛tol=1e-3,         # 早停容忍度
)
label_spread.fit(X_train, y_train_semi)# 评估模型
y_pred = label_spread.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("\n测试集准确率: {:.4f}".format(accuracy))
print("分类报告:\n", classification_report(y_test, y_pred))# 查看标签传播效果
print("\n标签传播统计:")
print(f"实际使用的标注样本数: {sum(label_spread.label_distributions_[:, -1] == 0)}")
print(f"模型迭代次数: {label_spread.n_iter_}")

 2. 特征选择与稀疏学习

周志华《机器学习导论》第11章 特征选择与稀疏学习-CSDN博客

2.1 过滤式选择特征   挑k个特征

SelectKBest — scikit-learn 1.7.1 documentation

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest, chi2# 加载数据集
X, y = load_iris(return_X_y=True)# 创建SelectKBest实例
selector = SelectKBest(chi2, k=2)# 进⾏过滤式特征选择
X_new = selector.fit_transform(X, y)# 获取所选特征的索引
selected_features = selector.get_support(indices=True)
print("Selected features:", selected_features)

2.2 包裹式选择   确定模型后选择

SelectFromModel — scikit-learn 1.7.1 documentation

下例为 先确定一个L1逻辑回归  再对clf包裹式选择特征

from sklearn.datasets import load_irisfrom sklearn.feature_selection import SelectFromModelfrom sklearn.linear_model import LogisticRegression# 加载数据集
X, y = load_iris(return_X_y=True)# 创建Logistic回归模型实例
clf = LogisticRegression(solver='liblinear', penalty='l1', C=0.5)# 创建SelectFromModel实例
selector = SelectFromModel(clf, threshold='mean')# 进⾏包裹式特征选择
X_new = selector.fit_transform(X, y)# 获取所选特征的索引
selected_features = selector.get_support(indices=True)
print("Selected features:", selected_features)

2.3 嵌入式选择与L1正则化

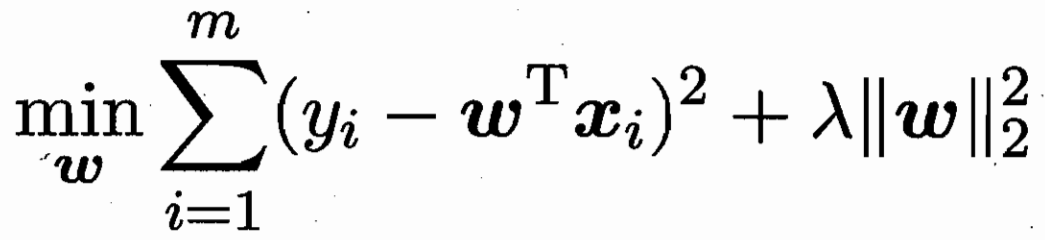
Lasso  L1  稀疏解             Ridge L2          模型中(alpha)为正则化前的系数

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso, Ridge# 加载数据集
X, y = load_iris(return_X_y=True)
X_train, test_x, y_train, test_lab = train_test_split(X,y,test_size = 0.4,random_state = 42)# 创建Lasso和ridge回归模型
lasso = Lasso(alpha=0.1)
ridge = Ridge(alpha=1.0)# 进⾏嵌⼊式特征选择
lasso.fit(X_train, y_train)
ridge.fit(X_train, y_train)# 输出所选特征的系数
coef = lasso.coef_
print("Feature coefficients:", coef)
coef1 = ridge.coef_
print("Feature coefficients:", coef1)#预测
lasso_pred = lasso.predict(test_x)
ridge_pred = ridge.predict(test_x)# 计算并打印评分（R²分数）
print("\nModel Performance:")
print(f"Lasso R² score: {lasso.score(test_x, test_lab):.4f}")
print(f"Ridge R² score: {ridge.score(test_x, test_lab):.4f}")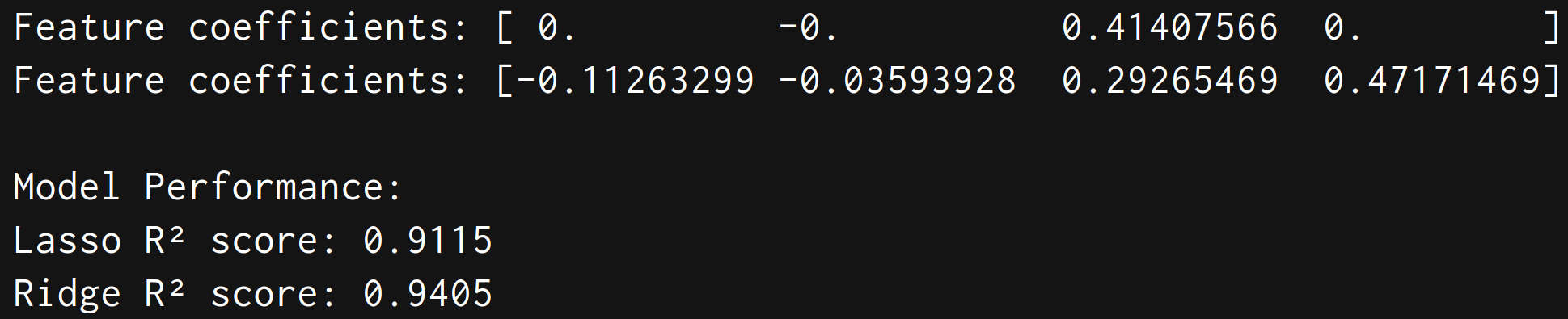

3. 聚类

周志华《机器学习导论》第9章 聚类-CSDN博客

3.1 K-means

k_means — scikit-learn 1.7.1 documentation

输入参数：

  • n_clusters: 要形成的簇数量，也是要生成的中心点数量

  • init: 初始化方法

    • 'k-means++' (默认): 智能初始化，加速收敛

    • 'random': 随机选择初始中心点

    • 也可以直接传入初始中心点坐标

  • n_init: 运行算法的次数(使用不同初始种子)，最终选择最佳结果

    • 'auto': 根据init自动选择(随机初始化运行10次，k-means++运行1次)

  • max_iter: 单次运行的最大迭代次数(默认300)

  • tol: 收敛阈值(连续两次迭代中心点变化的Frobenius范数)

输出：

  • cluster_centers_: 簇中心坐标

  • labels_: 每个样本的簇标签

from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler# 加载数据集
X = load_iris().data# 数据预处理
X_scaled = StandardScaler().fit_transform(X)
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X_scaled)# 获取聚类结果
print("Cluster labels:", kmeans.labels_)

3.2 DBSCAN

DBSCAN — scikit-learn 1.7.1 documentation

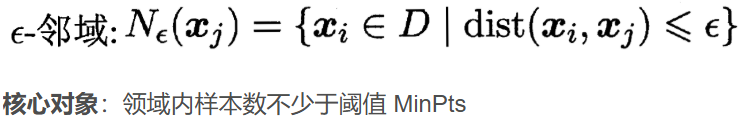
输入参数：

  • eps 邻域半径阈值，决定样本邻域范围
  • min_samples 核心点所需邻域内最少样本数
  • metric 距离度量方式，可选：- 'euclidean'（欧氏距离）- 'precomputed'（预计算距离矩阵）

输出：

  • core_sample_indices_       核心样本的索引 [n_core_samples]
  • components_       核心样本的特征值 [n_core_samples, n_features]
  • labels_      样本的簇标签（噪声点标记为-1） [n_samples] 
from sklearn.cluster import DBSCAN
import numpy as np
X = np.array([[1, 2], [2, 2], [2, 3],[8, 7], [8, 8], [25, 80]])
clustering = DBSCAN(eps=3, min_samples=2).fit(X)
print(clustering.labels_)  # 输出: [ 0  0  0  1  1 -1]

3.3 GMM 高斯混合聚类

GaussianMixture — scikit-learn 1.7.1 documentation

输入参数：

  • n_components  高斯混合成分数量
  • covariance_type  协方差矩阵类型： - 'full': 每个成分有自己的完全协方差矩阵 - 'tied': 所有成分共享相同协方差矩阵 - 'diag': 每个成分有对角协方差矩阵 - 'spherical': 每个成分有单一方差
  • tol   EM算法的收敛阈值
  • reg_covar   协方差对角线的正则化项
  • max_iter  最大迭代次数
  • n_init   初始化次数

输出：

  • weights_       每个混合成分的权重 [n_components]
  • means_        每个成分的均值 [n_components, n_features]
  • covariances_     协方差矩阵（形状取决于covariance_type）
  • predict(X)   预测样本所属成分
  • predict_proba(X)    预测样本属于各成分的概率
import numpy as np
from sklearn.mixture import GaussianMixture
X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]])
gm = GaussianMixture(n_components=2, random_state=0).fit(X)
print(gm.means_)
print(gm.predict([[0, 0], [12, 3]]))
print(gm.predict_proba([[0, 0], [12, 3]]))

4. sklearn.neighbors 邻居算法

sklearn.neighbors — scikit-learn 1.7.1 documentation

4.1 找最近的邻居

KDTree 递归地将 k维空间 沿数据方差最大的维度（坐标轴）进行二分，形成超矩形区域

BallTree 递归地将空间划分为 超球体（Hypersphere），每个节点代表一个球体区域。

4.2 KNN 最近k个邻居投票

KNeighborsClassifier — scikit-learn 1.7.1 documentation

  • n_neighbors    参与投票的最近邻居数量（K值）。
  • weights 权重设定     -'uniform'：所有邻居权重相等。 - 'distance'：权重为距离的倒数（越近影响越大）。- 自定义函数：输入距离数组，返回权重数组。
  • algorithm 邻居搜索算法： - 'ball_tree'/'kd_tree'：基于树结构，适合高维数据。 - 'brute'：暴力搜索，适合小数据集。 - 'auto'：自动选择最优算法。
  • metric   距离度量标准。常见选项： - 'euclidean'（L2）、'manhattan'（L1）。
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score#加载数据集
data, target = load_digits(return_data_target=True)#将数据集拆分为训练集（75%）和测试集（25%）:
train_x, test_x, train_y, test_y = train_test_split(data, target, test_size=0.25, random_state=33)knn = KNeighborsClassifier()
knn.fit(train_x, train_y)
predict_y = knn.predict(test_x) #计算模型准确度
score = accuracy_score(test_y, predict_y)
print(score)

5. PCA 主成分分析

先用make_blobs 生成几个簇集合

pca = PCA(n_components=k)  可以指定维度k    （≥1的话）

pca = PCA(n_components=0.95)  也可以指定解释的 方差比例之和至少解释多少 （<1的话）

pca = PCA(n_components=‘mle’) 基于最大似然估计自动选择维度

n_components_ 降维后的维度

explained_variance_ 降维后每个维度解释的方差

explained_variance_ratio_ 降维后每个维度解释的比例

from sklearn.datasets import make_blobs
# X为样本特征，Y为样本簇类别， 共10000个样本，每个样本3个特征，共4个簇
X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3,3, 3], [0,0,0], [1,1,1], [2,2,2]], cluster_std=[0.2, 0.1, 0.2, 0.2], random_state =9)#我们先不降维，只对数据进行投影，看看投影后的三个维度的方差分布，代码如下：
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)#现在我们来进行降维，从三维降到2维，代码如下：
pca = PCA(n_components=2)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)#现在我们看看不直接指定降维的维度，而指定降维后的主成分方差和比例。
print('n_components=0.95')
pca = PCA(n_components=0.95)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)print('n_components=0.99')
pca = PCA(n_components=0.99)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)print('n_components=mle')
pca = PCA(n_components='mle')
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)

核化PCA降维   KernelPCA      fit_transform(X)

稀疏 SparsePCA     选每个成分的时候 只有部分特征有贡献

from sklearn.decomposition import KernelPCA
from sklearn.datasets import load_iris# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target# 创建KernelPCA实例
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)# 进⾏核化线性降维
X_kpca = kpca.fit_transform(X)from sklearn.decomposition import SparsePCA
spca = SparsePCA(n_components=2, alpha=1, random_state=42)
spca.fit(X)
print("稀疏主成分:\n", spca.components_)
X_spca = spca.transform(X)

 

http://www.dtcms.com/a/320365.html

相关文章：

  • 【Canvas与徽章】北极星蓝盘玻璃光徽章
  • NumPy库向量的常见运算
  • C++面试9——多继承陷阱与适用场景
  • 【新闻资讯】Anthropic CEO 达里奥·阿莫迪万字访谈：在技术加速与风险防控间的坚守
  • vLLM：彻底改变大型语言模型推理延迟和吞吐量
  • RabbitMQ面试精讲 Day 14：Federation插件与数据同步
  • YOLOv8面试知识
  • Linux系统编程--基础开发工具
  • 容器之王--Docker的部署及基本操作演练
  • 前端学习 7：EDA 工具
  • Springboot 使用 JPA 分页查询
  • 前端开发工具大全
  • 车辆特征与车牌识别准确率↑29%：陌讯多模态融合算法实战解析
  • 知识蒸馏 - 基于KL散度的知识蒸馏 KL散度的方向
  • 适配器模式及优化
  • 在NVIDIA Orin上用TensorRT对YOLO12进行多路加速并行推理时内存泄漏 (中)
  • linux系统编程
  • 使用winsw把SpringBoot项目注册成window服务
  • javaweb开发之会话_过滤器_监听器
  • 【感知机】感知机(perceptron)学习算法的收敛性
  • 【Unity3D实例-功能-镜头】第三人称视觉-镜头优化
  • 基于深度学习的污水新冠RNA测序数据分析系统
  • Linux机器可直接使用的自动化编译文件
  • AGV_ads通讯exe的创建
  • Java日志技术：从基础到实战
  • 蒙文OCR识别技术难点实现及应用场景剖析
  • Transformer：Attention is all you need
  • HCIP | BGP综合实验报告册
  • PMP项目管理：理解PMP、PMP学什么 / 适合谁学 / Project Management Professional / 项目管理专业人士
  • uat是什么