计数组合学7.15（Schur 函数的经典定义 )

7.15 Schur 函数的经典定义

设 $\alpha =({\alpha }_1,\dots ,{\alpha }_n)\in {\mathbb{N}}^n$ 且 $w\in {\mathfrak{S}}_n$。照常记 $x^{\alpha }=x_1^{{\alpha }_1}\cdots x_n^{{\alpha }_n}$，并定义
$$w(x^{\alpha })=x_1^{{\alpha }_{w(1)}}\cdots x_n^{{\alpha }_{w(n)}}.$$
现定义
$$a_{\alpha }=a_{\alpha }(x_1,\dots ,x_n)=\sum _{w\in {\mathfrak{S}}_n}{\epsilon }_{w}w(x^{\alpha }),\text{\hspace{1em}(7.53)}$$
其中
$${\epsilon }_w=\{\begin{array}{ll}1,& \text{若 }w\text{ 为偶置换}\\ -1,& \text{若 }w\text{ 为奇置换}.\end{array}$$
（因此 ${\epsilon }_w={\epsilon }_{\rho (w)}$，如 (7.19) 所定义。）注意方程 (7.53) 的右边正是一个行列式的展开，即
$$a_{\alpha }=\det {\left(x_i^{{\alpha }_j}\right)}_{i,j=1}^n.$$
另注意 $a_{\alpha }$ 是斜对称的，即 $w(a_{\alpha })={\epsilon }_w{a}_{\alpha }$，故除非所有 ${\alpha }_i$ 互异，否则 $a_{\alpha }=0$。因此假设 ${\alpha }_1>{\alpha }_2>\cdots >{\alpha }_n\ge 0$，于是 $\alpha =\lambda +\delta$，其中 $\lambda \in \text{Par}$，$\ell (\lambda )\le n$，且 $\delta ={\delta }_n=(n-1,n-2,\dots ,0)$。由于 ${\alpha }_j={\lambda }_j+n-j$，我们得到
$$a_{\alpha }=a_{\lambda +\delta }=\det {\left(x_i^{{\lambda }_j+n-j}\right)}_{i,j=1}^n.\text{\hspace{1em}(7.54)}$$
例如，
$$a_{421}=a_{211+210}=\left|\begin{array}{ccc}{x}_1^4& x_1^2& x_1^1\\ x_2^4& x_2^2& x_2^1\\ x_3^4& x_3^2& x_3^1\end{array}\right|.$$

特别注意到
$$a_{\delta }=\det (x_i^{n-j})=\prod _{1\le i<j\le n}(x_i-x_j),\text{\hspace{1em}(7.55)}$$
即 Vandermonde 行列式。若在 $a_{\alpha }$ 中令 $i\ne j$ 时有 $x_i=x_j$，则由于 $a_{\alpha }$ 是斜对称的（或因为行列式 (7.54) 的第 $i$ 行与第 $j$ 行相等），我们得到 0。因此 $a_{\alpha }$ 可被 $x_i-x_j$ 整除，从而也可被 $a_{\delta }$ 整除（在环 $\mathbb{Z}[x_1,\dots ,x_n]$ 中）。故 $a_{\alpha }/a_{\delta }\in \mathbb{Z}[x_1,\dots ,x_n]$。此外，由于 $a_{\alpha }$ 和 $a_{\delta }$ 是斜对称的，其商是对称的，且显然是齐次的，次数为 $|\alpha |-|\delta |=|\lambda |$。换言之，$a_{\alpha }/a_{\delta }\in {\Lambda }_n^{|\lambda |}$。（商 $a_{\alpha }/a_{\delta }$ 称为 双交错式 (bialternant)。）因此很自然地要问 $a_{\alpha }/a_{\delta }$ 与我们已考虑的对称函数之间的关系。答案是对称函数理论中的一个基本结果。

7.15.1 定理

我们有
$$a_{\lambda +\delta }/a_{\delta }=s_{\lambda }(x_1,\dots ,x_n).$$

证明。此结果有多种证明。我们给出一种可推广到斜 Schur 函数的重要结果（定理 7.15.4）的证明。

对 (7.46) 应用 $\omega$ 并将 $\lambda$ 替换为 ${\lambda }^{\prime }$ 得
$$e_{\mu }=\sum _{\lambda }{K}_{{\lambda }^{\prime }\mu }{s}_{\lambda }.$$
由于矩阵 $(K_{{\lambda }^{\prime }\mu })$ 可逆，只需证明
$$e_{\mu }(x_1,\dots ,x_n)=\sum _{\lambda }{K}_{{\lambda }^{\prime }\mu }\frac{a_{\lambda +\delta }}{a_{\delta }},$$
或等价地（始终在 $n$ 个变量下工作），
$$a_{\delta }{e}_{\mu }=\sum _{\lambda }{K}_{{\lambda }^{\prime }\mu }{a}_{\lambda +\delta }.\text{\hspace{1em}(7.56)}$$
由于 (7.56) 两边均为斜对称，只需证明 $a_{\delta }{e}_{\mu }$ 中 $x^{\lambda +\delta }$ 的系数为 $K_{{\lambda }^{\prime }\mu }$。我们通过逐次乘以 $e_{{\mu }_1},e_{{\mu }_2},\dots$ 将 $a_{\delta }$ 与 $e_{\mu }$ 相乘。每个部分积 $a_{\delta }{e}_{{\mu }_1}\cdots e_{{\mu }_k}$ 是斜对称的，故出现在 $a_{\delta }{e}_{{\mu }_1}\cdots e_{{\mu }_k}$ 中的任意项 $x_1^{i_1}\cdots x_n^{i_n}$ 的所有指数 $i_j$ 互异。当我们将此项 $x_1^{i_1}\cdots x_n^{i_n}$ 与来自 $e_{{\mu }_{k+1}}$ 的一项 $x_{m_1}\cdots x_{m_j}$（其中 $j={\mu }_{k+1}$) 相乘时，要么两个指数相等（此时该项从 $a_{\delta }{e}_{{\mu }_1}\cdots e_{{\mu }_{k+1}}$ 中消失），要么指数保持严格递减顺序。因此要得到项 $x^{\lambda +\delta }$，我们必须从 $a_{\delta }$ 中的项 $x^{\delta }$ 开始，并逐次乘以 $e_{{\mu }_1}$ 的一项 $x^{{\alpha }^1}$，然后 $e_{{\mu }_2}$ 的一项 $x^{{\alpha }^2}$ 等，同时保持指数严格递减。此方式的数目即为 $a_{\delta }{e}_{\mu }$ 中 $x^{\lambda +\delta }$ 的系数。

给定上述项 $x^{{\alpha }^1},x^{{\alpha }^2},\dots$，定义半标准 Young 表 (SSYT) $T=T({\alpha }^1,{\alpha }^2,\dots )$ 如下：若变量 $x_j$ 出现在 $x^{{\alpha }^i}$ 中（即 ${\alpha }^i$ 的第 $j$ 个分量为 1），则 $T$ 的第 $j$ 列包含一个 $i$。例如，设 $n=4$，$\lambda =5332$，${\lambda }^{\prime }=44311$，$\lambda +\delta =8542$，$\mu =3222211$，$x^{{\alpha }^1}=x_1{x}_2{x}_3$，$x^{{\alpha }^2}=x_1{x}_2$，$x^{{\alpha }^3}=x_3{x}_4$，$x^{{\alpha }^4}=x_1{x}_2$，$x^{{\alpha }^5}=x_1{x}_4$，$x^{{\alpha }^6}=x_1$，$x^{{\alpha }^7}=x_3$。则 $T$ 由下式给出：

易见映射 $({\alpha }^1,{\alpha }^2,\dots )\mapsto T({\alpha }^1,{\alpha }^2,\dots )$ 建立了从 $x^{\delta }$ 按上述规则构造项 $x^{\lambda +\delta }$ 的方式与形状为 ${\lambda }^{\prime }$ 且类型为 $\mu$ 的 SSYT 之间的双射，故证明完成。 □

由 Schur 函数的组合定义可知，若 $\ell (\lambda )>n$，则 $s_{\lambda }(x_1,\dots ,x_n)=0$。由于根据命题 7.8.2(a) 有 dim⁡Λn=#{λ∈Par:ℓ(λ)≤n}\dim \Lambda_n = \#\{\lambda \in \text{Par} : \ell(\lambda) \leq n\}dimΛn​=#{λ∈Par:ℓ(λ)≤n}，故集合 {sλ(x1,…,xn):ℓ(λ)≤n}\{s_{\lambda}(x_1, \ldots, x_n) : \ell(\lambda) \leq n\}{sλ​(x1​,…,xn​):ℓ(λ)≤n} 构成 ${\Lambda }_n$ 的一组基。（这也可由推论 7.10.6 证明的简单推广得到。）我们在 ${\Lambda }_n$ 上定义内积 $⟨,{⟩}_n$，要求 {sλ(x1,…,xn):ℓ(λ)≤n}\{s_{\lambda}(x_1, \ldots, x_n) : \ell(\lambda) \leq n\}{sλ​(x1​,…,xn​):ℓ(λ)≤n} 是标准正交基。若 $f,g\in \Lambda$，则简记 $⟨f,g{⟩}_n$ 为 $⟨f(x_1,\dots ,x_n),g(x_1,\dots ,x_n){⟩}_n$。因此
$$⟨f,g⟩=⟨f,g{⟩}_n,$$
前提是 $f$ 中出现的每个单项式至多涉及 $n$ 个不同变量，例如若 $\mathrm{deg}f\le n$。

7.15.2 推论

若 $f\in {\Lambda }_n$，$\ell (\lambda )\le n$，且 $\delta =(n-1,n-2,\dots ,1,0)$，则
$$⟨f,s_{\lambda }{⟩}_n=[x^{\lambda +\delta }]a_{\delta }f,$$
即 $a_{\delta }f$ 中 $x^{\lambda +\delta }$ 的系数。

证明。所有函数均在变量 $x_1,\dots ,x_n$ 中。设 $f={\sum }_{\ell (\lambda )\le n}{c}_{\lambda }{s}_{\lambda }$。则由定理 7.15.1 有
$$a_{\delta }f=\sum _{\ell (\lambda )\le n}{c}_{\lambda }{a}_{\lambda +\delta },$$
故
$$⟨f,s_{\lambda }{⟩}_n=c_{\lambda }=[x^{\lambda +\delta }]a_{\delta }f.$$ □

例如，对于 $\ell (\lambda )\le n$，有
$$⟨a_{\delta }^{2k},s_{\lambda }{⟩}_n=[x^{\lambda +\delta }]a_{\delta }^{2k+1}.\text{\hspace{1em}(7.57)}$$
计算数 (7.57) 是一个有趣的问题（仅部分解决）；有关 $k=1$ 情形的进一步信息，参见练习 37。

现在考虑定理 7.15.1 的“斜推广”。我们继续在 $n$ 个变量 $x_1,\dots ,x_n$ 下工作。对任意 $\lambda ,v\in \text{Par}$，$\ell (\lambda )\le n$，$\ell (v)\le n$，考虑展开式
$$s_v{e}_{\mu }=\sum _{\lambda }{L}_{v^{\prime }\mu }^{\lambda }{s}_{\lambda },$$
或等价地（乘以 $a_{\delta }$)，
$$a_{v+\delta }{e}_{\mu }=\sum _{\lambda }{L}_{v^{\prime }\mu }^{\lambda }{a}_{\lambda +\delta }.\text{\hspace{1em}(7.58)}$$

如定理 7.15.1 证明中的论证表明，$L_{v^{\prime }\mu }^{\lambda }$ 等于以下方式的数目：
$$\lambda +\delta =v+\delta +{\alpha }^1+{\alpha }^2+\cdots +{\alpha }^k,$$
其中 $\ell (\mu )=k$，每个 ${\alpha }^i$ 是含 ${\mu }_i$ 个 1 的 $(0,1)$-向量，且每个部分和 $v+\delta +{\alpha }^1+\cdots +{\alpha }^i$ 的坐标严格递减。定义形状为 ${\lambda }^{\prime }/v^{\prime }$ 且类型为 $\mu$ 的斜 SSYT $T=T_{\lambda }/v({\alpha }^1,\dots ,{\alpha }^k)$，其条件为：若 ${\alpha }^i$ 的第 $j$ 个分量为 1，则 $i$ 出现在 $T$ 的第 $j$ 列。这建立了一个双射，表明 $L_{v^{\prime }\mu }^{{\lambda }^{\prime }}$ 等于斜 Kostka 数 $K_{{\lambda }^{\prime }/v^{\prime },\mu }$，即形状为 ${\lambda }^{\prime }/v^{\prime }$ 且类型为 $\mu$ 的斜 SSYT 的数量（见方程 (7.36)）。（若 $v^{\prime }⊈{\lambda }^{\prime }$，则此数为 0。）

7.15.3 推论

我们有
$$s_v{e}_{\mu }=\sum _{\lambda }{K}_{{\lambda }^{\prime }/v^{\prime },\mu }{s}_{\lambda }.\text{\hspace{1em}(7.59)}$$

证明。将 (7.58) 除以 $a_{\delta }$，并令 $n\to \infty$。□

现在容易建立斜 Schur 函数的一个基本性质。

7.15.4 定理

对任意 $f\in \Lambda$，我们有
$$⟨f{s}_v,s_{\lambda }⟩=⟨f,s_{\lambda /v}⟩.$$
换言之，由 $M_{v}f=s_{v}f$ 和 $D_v{s}_{\lambda }=s_{\lambda /v}$ 定义的两种线性变换 $M_v:\Lambda \to \Lambda$ 与 $D_v:\Lambda \to \Lambda$ 关于内积 $⟨,⟩$ 互为伴随。特别地，
$$⟨s_{\mu }{s}_v,s_{\lambda }⟩=⟨s_{\mu },s_{\lambda /v}⟩.\text{\hspace{1em}(7.60)}$$

证明。对 (7.59) 应用 $\omega$，并将 $v$ 替换为 $v^{\prime }$，$\lambda$ 替换为 ${\lambda }^{\prime }$。我们得到
$$s_v{h}_{\mu }=\sum _{\lambda }{K}_{\lambda /v,\mu }{s}_{\lambda }.$$
因此
$$⟨s_v{h}_{\mu },s_{\lambda }⟩=K_{\lambda /v,\mu }=⟨h_{\mu },s_{\lambda /v}⟩,\text{\hspace{1em}(7.61)}$$
由 (7.36) 及 $⟨h_{\mu },m_{\rho }⟩={\delta }_{\mu \rho }$（由 $⟨,⟩$ 的定义）可得。但方程 (7.61) 在 $h_{\mu }$ 上是线性的，故由于 {hμ}\{ h_\mu \}{hμ​} 是 $\Lambda$ 的一组基，证明完成。□

7.15.5 例子

我们有 $s_1{s}_{31}=s_{41}+s_{32}+s_{311}$ 和 $s_1{s}_{22}=s_{32}+s_{221}$。其他乘积 $s_1{s}_{\mu }$ 均不涉及 $s_{32}$。由此可得 $s_{32/1}=s_{22}+s_{31}$。关于推广，参见推论 7.15.9。

现在我们可以给出定理 7.14.5 到斜 Schur 函数的推广。

7.15.6 定理

对任意 $\lambda ,v\in \text{Par}$，我们有 $\omega s_{\lambda /v}=s_{{\lambda }^{\prime }/v^{\prime }}$。

证明。由命题 7.9.5 和方程 (7.60)，有
$$⟨\omega (s_{\mu }{s}_v),\omega s_{\lambda }⟩=⟨\omega s_{\mu },\omega s_{\lambda /v}⟩.$$
故由定理 7.14.5 得
$$⟨s_{{\mu }^{\prime }}{s}_{v^{\prime }},s_{{\lambda }^{\prime }}⟩=⟨s_{{\mu }^{\prime }},\omega s_{\lambda /v}⟩.\text{\hspace{1em}(7.62)}$$
另一方面，在 (7.60) 中分别将 ${\lambda }^{\prime },{\mu }^{\prime },v^{\prime }$ 替换为 $\lambda ,\mu ,v$ 得
$$⟨s_{{\mu }^{\prime }}{s}_{v^{\prime }},s_{{\lambda }^{\prime }}⟩=⟨s_{{\mu }^{\prime }},s_{{\lambda }^{\prime }/v^{\prime }}⟩.\text{\hspace{1em}(7.63)}$$
由 (7.62) 和 (7.63) 可得 $\omega s_{\lambda /v}=s_{{\lambda }^{\prime }/v^{\prime }}$。□

整数 $⟨s_{\lambda },s_{\mu }{s}_{\nu }⟩=⟨s_{\lambda /\nu },s_{\mu }⟩=⟨s_{\lambda /\mu },s_{\nu }⟩$ 记为 $c_{\mu \nu }^{\lambda }$，称为 Littlewood-Richardson 系数。因此
$$s_{\mu }{s}_{\nu }=\sum _{\lambda }{c}_{\mu \nu }^{\lambda }{s}_{\lambda }$$
$$s_{\lambda /\nu }=\sum _{\mu }{c}_{\mu \nu }^{\lambda }{s}_{\mu }$$
$$s_{\lambda /\mu }=\sum _{\nu }{c}_{\mu \nu }^{\lambda }{s}_{\nu }.$$
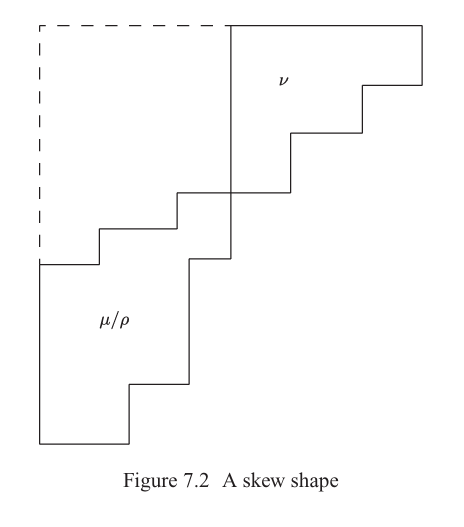
注意，看似更一般的 $⟨s_{\lambda /\nu },s_{\mu /\rho }⟩$ 本身就是一个 Littlewood-Richardson 系数，因为 $⟨s_{\lambda /\nu },s_{\mu /\rho }⟩=⟨s_{\lambda },s_{\nu }{s}_{\mu /\rho }⟩$ 且 $s_{\nu }{s}_{\mu /\rho }$ 恰是一个斜 Schur 函数，如图 7.2（结合 Schur 函数的组合定义）所明示。更一般地，任意斜 Schur 函数的乘积仍是一个斜 Schur 函数。

对称函数理论的一个核心结果，称为 Littlewood-Richardson 法则，给出了 Littlewood-Richardson 系数 $c_{\mu \nu }^{\lambda }$ 的组合解释。我们将 Littlewood-Richardson 法则的陈述和证明推迟到附录 1（§A1.5）。此处我们考虑当 $\mu =(n)$（即仅有一个部分等于 $n$ 的分拆）时更简单的特殊情形。为表述此结果（称为 Pieri 法则），定义一个水平条 (horizontal strip) 为一个斜形状 $\lambda /\nu$，其任意两格不在同一列中。因此，一个形状为 $\mu /\rho$ 且最大部分不超过 $m$ 的 SSYT 可视为一个分拆序列 $\rho ={\mu }^0\subseteq {\mu }^1\subseteq \cdots \subseteq {\mu }^m=\mu$，其中每个斜形状 ${\mu }^i/{\mu }^{i-1}$ 是一个水平条。（只需将 $i$ 插入 ${\mu }^i/{\mu }^{i-1}$ 的每一格。）

7.15.7 定理

我们有
$$s_{\nu }{s}_n=\sum _{\lambda }{s}_{\lambda },\text{\hspace{1em}(7.65)}$$
其中求和遍历所有满足 $\lambda /\nu$ 是大小为 $n$ 的水平条的分拆 $\lambda$。

证明。我们有 $⟨s_{\nu }{s}_n,s_{\lambda }⟩=⟨s_n,s_{\lambda /\nu }⟩=⟨h_n,s_{\lambda /\nu }⟩=K_{\lambda /\nu ,n}$。显然由 $K_{\lambda /\nu ,n}$ 的定义有
$$K_{\lambda /\nu ,n}=\{\begin{array}{ll}1,& \text{若 }\lambda /\nu \text{ 是大小为 }n\text{ 的水平条}\\ 0,& \text{否则,}\end{array}$$
故证明完成。 □

7.15.8 例子

设 $v=331$ 且 $n=2$。将大小为 2 的水平条添加到形状 331 的方式由下式给出：

因此
$$s_{331}{s}_2=s_{531}+s_{432}+s_{4311}+s_{333}+s_{3321}.$$
注意，对 (7.65) 应用 $\omega$ 可得 Pieri 法则的对偶形式。即，以显然方式定义一个垂直条 (vertical strip)，我们有
$$s_v{s}_{1^n}=s_v{e}_n=\sum _{\lambda }{s}_{\lambda },\text{\hspace{1em}(7.66)}$$
其中求和遍历所有满足 $\lambda /v$ 是大小为 $n$ 的垂直条的分拆 $\lambda$。

作为 (7.60) 和 Pieri 法则（定理 7.15.7）的直接推论，我们还有以下 Pieri 法则的斜版本。

7.15.9 推论

我们有
$$s_{\lambda /(n)}=\sum _{\nu }{s}_{\nu },$$
其中 $v$ 遍历所有满足 $\lambda /v$ 是大小为 $n$ 的水平条的分拆 $v\subseteq \lambda$。

我们给出的 Pieri 法则证明相当间接，但 Pieri 法则实际上是一个简单的组合陈述，值得一个直接的双射证明。设 ${\mathcal{T}}_{v,n}^{\alpha }$ 为所有满足 $\text{sh}(T)=v$，$\text{sh}(T^{\prime })=(n)$ 且 $\text{type}(T)+\text{type}(T^{\prime })=\alpha$ 的 SSYT 对 $(T,T^{\prime })$ 的集合。类似地，设 ${\mathcal{T}}_{\lambda }^{\alpha }$ 为所有满足 $\text{sh}(T)=\lambda$ 且 $\text{type}(T)=\alpha$ 的 SSYT $T$ 的集合。Pieri 法则断言
$$\#{\mathcal{T}}_{v,n}^{\alpha }=\#\left(\bigcup _{\lambda }{\mathcal{T}}_{\lambda }^{\alpha }\right),$$
其中 $\lambda$ 遍历所有满足 $\lambda /v$ 是大小为 $n$ 的水平条的分拆。因此我们寻求一个双射
$$\phi :{\mathcal{T}}_{v,n}^{\alpha }\to \bigcup _{\lambda }{\mathcal{T}}_{\lambda }^{\alpha }.$$
设 $T^{\prime }=a_1{a}_2\cdots a_n$。不难证明（使用引理 7.11.2）$\phi$ 恰由迭代行插入给出：
$$\phi (T,T^{\prime })=((T\leftarrow a_1)\leftarrow a_2)\leftarrow \cdots \leftarrow a_n.$$

定理 7.15.4 的进一步体现如下。令 $\Lambda (x)$ 和 $\Lambda (y)$ 分别表示变量 $x=(x_1,x_2,\dots )$ 和 $y=(y_1,y_2,\dots )$ 中的对称函数环。记 $\Lambda (x)\otimes \Lambda (y)$ 为在 $x$ 和 $y$ 变量中对称的有界次数形式幂级数（系数为 $\mathbb{Q}$) 的环。换言之，若 $f(x_1,x_2,\dots ;y_1,y_2,\dots )\in \Lambda (x)\otimes \Lambda (y)$ 且 $u$ 和 $v$ 均为 $\mathbb{P}$ 的置换，则
$$f(x_1,x_2,\dots ;y_1,y_2,\dots )=f(x_{u(1)},x_{u(2)},\dots ;y_{v(1)},y_{v(2)},\dots ).$$
显然，若 {bμ(x)}\{b_\mu(x)\}{bμ​(x)} 是 $\Lambda (x)$ 的一组基且 {cv(y)}\{c_v(y)\}{cv​(y)} 是 $\Lambda (y)$ 的一组基，则 {bμ(x)cv(y)}\{b_\mu(x)c_v(y)\}{bμ​(x)cv​(y)} 是 $\Lambda (x)\otimes \Lambda (y)$ 的一组基。在 $x$ 和 $y$ 变量中对称的有界次数形式幂级数的环 $\Lambda (x,y)$ 是 $\Lambda (x)\otimes \Lambda (y)$ 的一个子代数。当然此包含关系是真包含；例如，若 $f(x)\in \Lambda (x)$ 且 $\mathrm{deg}f>0$，则 $f(x)\in \Lambda (x)\otimes \Lambda (y)$ 但 $f(x)\notin \Lambda (x,y)$。若 {bλ(x)}\{b_\lambda(x)\}{bλ​(x)} 是 $\Lambda (x)$ 的一组基，则 {bλ(x,y)}\{b_\lambda(x, y)\}{bλ​(x,y)} 是 $\Lambda (x,y)$ 的一组基，其中 $b_{\lambda }(x,y)$ 表示变量 $x_1,x_2,\dots$ 和 $y_1,y_2,\dots$ 中的对称函数 $b_{\lambda }$。现在很自然地要问如何在 $\Lambda (x)\otimes \Lambda (y)$ 的基 {sμ(x)sν(y)}\{s_\mu(x)s_\nu(y)\}{sμ​(x)sν​(y)} 下展开 $s_{\lambda }(x,y)$。考虑有序字母表 A={1<2<⋯<1′<2′<⋯ }A = \{1 < 2 < \cdots < 1' < 2' < \cdots\}A={1<2<⋯<1′<2′<⋯}。若 $T$ 是此字母表中形状为 $\lambda$ 的 SSYT，则定义
$$(xy{)}^T=x_1^{\#(1)}{x}_2^{\#(2)}\cdots y_1^{\#(1^{\prime })}{y}_2^{\#(2^{\prime })}\cdots ,$$
其中 $\#(a)$ 表示 $a$ 在 $T$ 中出现的次数。因此由 $s_{\lambda }$ 的组合定义（定义 7.10.1），有
$$s_{\lambda }(x,y)=\sum _T(xy{)}^T,$$
其中 $T$ 遍历字母表 $A$ 中形状为 $\lambda$ 的所有 SSYT。现在 $T$ 中被 $1,2,\dots$ 占据的部分恰是某个形状 $\mu \subseteq \lambda$ 的 SSYT，而被 $1^{\prime },2^{\prime },\dots$ 占据的部分是形状 $\lambda /\mu$ 的斜 SSYT。由此观察可得
$$s_{\lambda }(x,y)=\sum _{\mu \subseteq \lambda }{s}_{\mu }(x)s_{\lambda /\mu }(y)\text{\hspace{1em}(7.67)}$$
$$=\sum _{\mu \subseteq \lambda }{s}_{\mu }(x)\sum _v{c}_{\mu v}^{\lambda }{s}_v(y)$$
$$=\sum _{\mu ,v}{c}_{\mu v}^{\lambda }{s}_{\mu }(x)s_v(y),$$
这给出了我们所需的展开式。

注（供代数学者参考）。定义 $\Delta :\Lambda \to \Lambda (x)\otimes \Lambda (y)$ 为 $\Delta f=f(x,y)$。此运算使空间 $\Lambda$ 成为一个余代数，与 $\Lambda$ 上通常的代数结构一起构成一个双代数。若取 $1\in \Lambda$ 为单位元，并取映射 $f\mapsto f(0,0,\dots )$ 为余单位元，则我们得到一个 Hopf 代数。此外，$\Lambda$ 上的内积与双代数结构相容，即
$$⟨\Delta f,g(x)h(y)⟩=⟨f,gh⟩.\text{\hspace{1em}(7.68)}$$
此处第一个内积在 $\Lambda (x)\otimes \Lambda (y)$ 中进行，其中元素 $s_{\mu }(x)s_{\nu }(y)$ 构成标准正交基。第二个内积恰为 $\Lambda$ 上的通常内积。