机器学习——04 逻辑回归
1 逻辑回归简介
1.1 应用场景
-
逻辑回归是一种常用于解决二分类问题的机器学习算法,也就是把数据分成两个类别;
-
应用场景1:预测疾病的情况,比如判断是否感染新冠病毒,就是在“是阳性”和“不是阳性”这两个类别里做判断。逻辑回归可以通过分析一些相关的特征数据,来预测一个人是否可能患病;

-
应用场景2:银行信贷贷款,银行在决定是否放贷时,会考虑很多因素,像借款人的信用状况、还款能力等。逻辑回归能帮助银行把申请人分成“放贷”和“不放贷”这两类,辅助做出决策;

-
应用场景3:情感分析,比如分析用户对某个产品、服务或者事件的评价是正面的还是负面的。通过对文本等数据的处理,逻辑回归可以判断出情感倾向属于“正面”或者“负面”;

-
应用场景4:预测广告点击率,就是判断用户会不会点击某个广告,分为“点击”和“不点击”两类。这对于优化广告投放策略很有帮助,能提高广告的效果;

-
其它应用场景:垃圾邮件的识别(是垃圾邮件、不是垃圾邮件)、电商中的客户是否会购买商品(购买、不购买)等等。
1.2 数学基础
1.2.1 sigmoid函数
-
数学公式:
f(x)=11+e−x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1- 其中,eee 是自然对数的底数,约等于 2.71828;
-
作用:
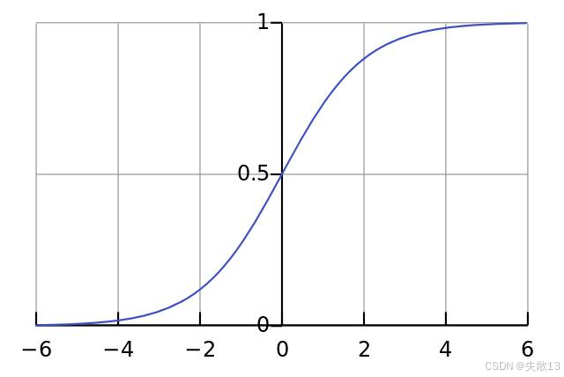
- sigmoid函数能够将输入值 xxx(其取值范围为 (−∞,+∞)(-\infty, +\infty)(−∞,+∞))映射到区间 (0,1)(0, 1)(0,1) 内;
- 这一特性使得它在逻辑回归中非常有用,因为逻辑回归的目标通常是预测一个事件发生的概率,而概率的取值范围正好是 (0,1)(0, 1)(0,1);
- 例如,在预测疾病是否发生时,我们可以将模型的输出通过 sigmoid 函数转换为一个介于 0 和 1 之间的值,这个值可以被解释为患病的概率;
-
数学性质:
- 单调递增函数:sigmoid函数是单调递增的,这意味着当输入 xxx 增大时,函数的输出值也随之增大。这种单调性在逻辑回归中保证了模型的预测结果具有一定的合理性,例如,随着某些特征值的增加,预测的概率也会相应地增加;
- 拐点:上图中当 x=0x = 0x=0 时,f(0)=11+e0=0.5f(0) = \frac{1}{1 + e^{0}} = 0.5f(0)=1+e01=0.5,并且在这一点函数的增长速度发生了变化,所以 x=0,y=0.5x = 0, y = 0.5x=0,y=0.5 是函数的拐点;
-
导函数公式:
f′(x)=f(x)(1−f(x)) f^\prime(x) = f(x)(1 - f(x)) f′(x)=f(x)(1−f(x))- 这个导函数在逻辑回归的参数优化过程中非常重要;
- 在使用梯度下降等优化算法来训练逻辑回归模型时,需要计算损失函数关于模型参数的梯度,而 sigmoid 函数的导函数可以简化这一计算过程。
1.2.2 概率
-
概率:
- 概率是用来衡量事件发生可能性大小的数值;
- 例如,北京早上堵车的可能性 PA=0.7P_A = 0.7PA=0.7,中午堵车的可能性 PB=0.3P_B = 0.3PB=0.3,晚上堵车的可能性 PC=0.4P_C = 0.4PC=0.4;
-
联合概率:
- 联合概率指的是两个或多个随机变量同时发生的概率;
- 例如,已知北京早上堵车的概率 PA=0.7P_A = 0.7PA=0.7,如果假设每周各天早上堵车的概率相互独立,那么周1早上和周2早上同时堵车的概率可以通过计算联合概率得到,即 PA∩B=PA×PB=0.7×0.7=0.49P_{A \cap B} = P_A \times P_B = 0.7 \times 0.7 = 0.49PA∩B=PA×PB=0.7×0.7=0.49;
-
条件概率:
- 条件概率表示在事件 BBB 已经发生的条件下,事件 AAA 发生的概率,记为 P(A∣B)P(A|B)P(A∣B);
- 例如:
- 已知北京早上堵车的概率 PA=0.7P_A = 0.7PA=0.7,中午堵车的概率 PB=0.3P_B = 0.3PB=0.3,那么在周1早上已经堵车的情况下,中午再堵车的概率可以表示为 P(B∣A)P(B|A)P(B∣A);
- 根据条件概率的计算公式 P(B∣A)=P(A∩B)P(A)P(B|A) = \frac{P(A \cap B)}{P(A)}P(B∣A)=P(A)P(A∩B),在假设早上和中午堵车事件相互独立的情况下,P(A∩B)=PA×PBP(A \cap B) = P_A \times P_BP(A∩B)=PA×PB,所以 P(B∣A)=PA×PBPA=PB=0.3P(B|A) = \frac{P_A \times P_B}{P_A} = P_B = 0.3P(B∣A)=PAPA×PB=PB=0.3。
1.2.3 极大似然估计
-
核心思想:极大似然估计的核心思想是根据观测到的结果来估计模型算法中的未知参数。也就是说,我们认为已经观测到的事件是最有可能发生的,因此需要找到一组参数,使得在这组参数下,观测到的事件发生的概率最大;
-
举个栗子:假设有一枚不均匀的硬币,出现正面的概率为 θ\thetaθ,反面的概率为 1−θ1 - \theta1−θ。抛了 6 次得到的结果为 D={正面,反面,反面,正面,正面,正面}D = \{正面, 反面, 反面, 正面, 正面, 正面\}D={正面,反面,反面,正面,正面,正面},且每次投掷事件相互独立;
- 首先,计算在参数 θ\thetaθ 下,观测到结果 DDD 的概率 P(D∣θ)P(D|\theta)P(D∣θ)。因为每次投掷相互独立,所以:
P(D∣θ)=P(正面∣θ)×P(反面∣θ)×P(反面∣θ)×P(正面∣θ)×P(正面∣θ)×P(正面∣θ)=θ×(1−θ)×(1−θ)×θ×θ×θ=θ4(1−θ)2 \begin{align*} P(D|\theta) &= P(正面|\theta) \times P(反面|\theta) \times P(反面|\theta) \times P(正面|\theta) \times P(正面|\theta) \times P(正面|\theta) \\ &= \theta \times (1 - \theta) \times (1 - \theta) \times \theta \times \theta \times \theta \\ &= \theta^4(1 - \theta)^2 \end{align*} P(D∣θ)=P(正面∣θ)×P(反面∣θ)×P(反面∣θ)×P(正面∣θ)×P(正面∣θ)×P(正面∣θ)=θ×(1−θ)×(1−θ)×θ×θ×θ=θ4(1−θ)2 - 接下来,问题转化为求这个函数的极大值时,θ\thetaθ 的取值是多少。为了找到极大值点,我们对 f(θ)=θ4(1−θ)2f(\theta) = \theta^4(1 - \theta)^2f(θ)=θ4(1−θ)2 求导,并令导数等于 0:
f′(θ)=4θ3(1−θ)2+θ4×2(1−θ)(−1)=4θ3(1−θ)2−2θ4(1−θ)=θ3(1−θ)(4(1−θ)−2θ)=θ3(1−θ)(4−6θ) \begin{align*} f^\prime(\theta) &= 4\theta^3(1 - \theta)^2 + \theta^4 \times 2(1 - \theta)(-1) \\ &= 4\theta^3(1 - \theta)^2 - 2\theta^4(1 - \theta) \\ &= \theta^3(1 - \theta)(4(1 - \theta) - 2\theta) \\ &= \theta^3(1 - \theta)(4 - 6\theta) \end{align*} f′(θ)=4θ3(1−θ)2+θ4×2(1−θ)(−1)=4θ3(1−θ)2−2θ4(1−θ)=θ3(1−θ)(4(1−θ)−2θ)=θ3(1−θ)(4−6θ)- 令 f′(θ)=0f^\prime(\theta) = 0f′(θ)=0,则有 θ3=0\theta^3 = 0θ3=0,1−θ=01 - \theta = 01−θ=0 或 4−6θ=04 - 6\theta = 04−6θ=0,解得 θ1=0\theta_1 = 0θ1=0,θ2=1\theta_2 = 1θ2=1,θ3=23\theta_3 = \frac{2}{3}θ3=32;
- 然后,我们需要判断这些解中哪个是极大值点。通过分析函数的单调性或者二阶导数等方法可以确定,θ3=23\theta_3 = \frac{2}{3}θ3=32 是函数的极大值点。因此,根据极大似然估计,这枚不均匀硬币出现正面的概率 θ\thetaθ 估计为 23\frac{2}{3}32。
- 首先,计算在参数 θ\thetaθ 下,观测到结果 DDD 的概率 P(D∣θ)P(D|\theta)P(D∣θ)。因为每次投掷相互独立,所以:
1.2.4 对数函数
-
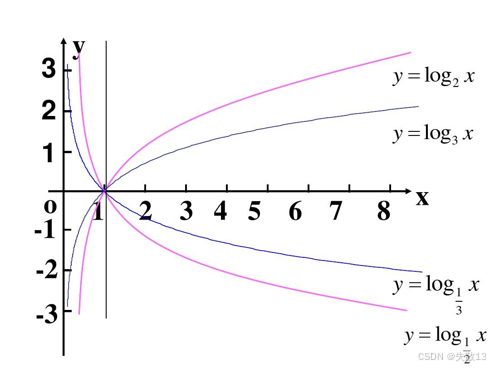
对数函数的定义:
-
如果 ab=Na^b = Nab=N(其中 a>0a > 0a>0,b≠1b \neq 1b=1),那么 bbb 叫做以 aaa 为底 NNN 的对数,记为 b=logaNb = \log_a Nb=logaN;
-
例如,log10100=2\log_{10} 100 = 2log10100=2,因为 102=10010^2 = 100102=100;log216=4\log_2 16 = 4log216=4,因为 24=162^4 = 1624=16;
-
-
对数函数的性质:
- loga(MN)=logaM+logaN\log_a(MN) = \log_a M + \log_a Nloga(MN)=logaM+logaN:这一性质表明,两个数的乘积的对数等于这两个数的对数之和;
- logaMN=logaM−logaN\log_a \frac{M}{N} = \log_a M - \log_a NlogaNM=logaM−logaN:即两个数的商的对数等于这两个数的对数之差;
- logaMn=nlogaM\log_a M^n = n\log_a MlogaMn=nlogaM:一个数的 nnn 次方的对数等于 nnn 乘以这个数的对数;
- 其中,a>0a > 0a>0,a≠1a \neq 1a=1,M>0M > 0M>0,N>0N > 0N>0;
-
对数函数在逻辑回归中的应用:
- 从对数运算性质来看,它能够把几个概率联乘的式子,改成 log\loglog 相加的形式;
- 在逻辑回归中,当我们处理似然函数时,由于似然函数通常是多个概率的乘积,直接计算和优化比较困难;
- 通过取对数,我们可以将乘积转换为求和,从而简化计算,并且不改变函数的极值点位置(因为对数函数是单调递增的);
- 例如,在极大似然估计中,对似然函数取对数得到对数似然函数,然后通过最大化对数似然函数来估计模型参数,这一过程在计算上更加简便。
2 逻辑回归原理
2.1 概念
-
概念:
-
逻辑回归是一种分类模型,它将线性回归的输出作为自身的输入;
-
其输出是介于 (0,1)(0, 1)(0,1) 之间的值,这个值可以被解释为样本属于某一类别的概率;
-
例如,在二分类问题中,输出值越接近 1,样本属于正类的概率就越大;越接近 0,样本属于负类的概率就越大;
-
-
逻辑回归的分类过程:
-
利用线性模型计算特征值:
- 首先,使用线性模型 f(x)=wTx+bf(x) = w^T x + bf(x)=wTx+b,其中 www 是权重向量,xxx 是样本的特征向量,bbb 是偏置项;
- 这个线性模型根据特征的重要性(通过权重 www 体现)计算出一个值 f(x)f(x)f(x);
- 例如,在预测疾病是否发生的问题中,特征可能包括年龄、血压、血糖等指标,线性模型会根据这些特征的权重计算出一个综合得分;
-
使用 sigmoid 函数映射为概率值:然后,使用 sigmoid 函数将线性模型的输出 f(x)f(x)f(x) 映射为概率值。sigmoid 函数的表达式为:
sigmoid(z)=11+e−z \text{sigmoid}(z) = \frac{1}{1 + e^{-z}} sigmoid(z)=1+e−z1- 其中 z=wTx+bz = w^T x + bz=wTx+b。通过 sigmoid 函数,将线性模型的输出 zzz 转换为介于 0 和 1 之间的概率值 ppp,表示样本属于正类的概率;
-
设置阈值进行分类:
- 设置一个阈值(例如 0.5)。如果输出的概率值 ppp 大于 0.5,则将未知样本预测为 1 类(正类);
- 否则,预测为 0 类(负类)。阈值的选择可以根据具体问题进行调整,例如在某些对假阳性要求较高的场景中,可以将阈值设置得更高一些;
-
-
逻辑回归的假设函数:用于将输入特征映射到一个介于 0 和 1 之间的概率值(即上面过程的第二步),表示样本属于正类的可能性,公式如下
hw(x)=sigmoid(wTx+b) h_w(x) = \text{sigmoid}(w^T x + b) hw(x)=sigmoid(wTx+b)- 其中,wTx+bw^T x + bwTx+b 是线性回归的输出,作为逻辑回归的输入,经过 sigmoid 函数转换后得到样本属于正类的概率;
-
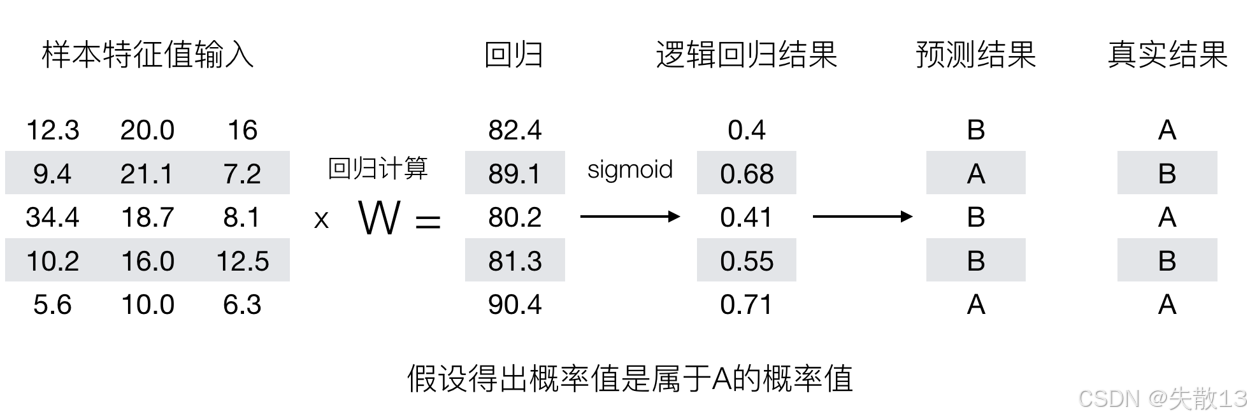
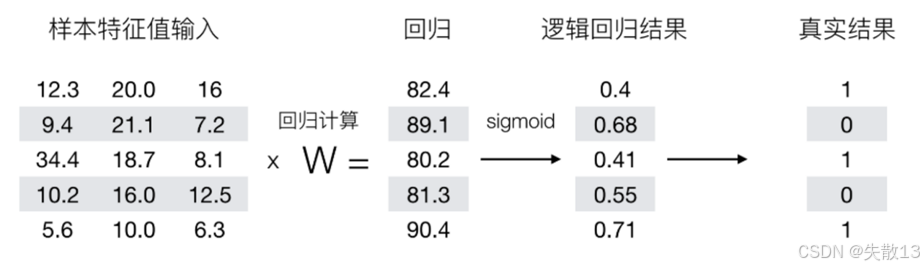
举个栗子:逻辑回归预测过程(阈值为 0.6)
-
样本特征值输入:给出了多个样本的特征值,例如第一行样本的特征值为 [12.3,20.0,16][12.3, 20.0, 16][12.3,20.0,16];
-
回归计算:通过样本特征值与权重向量 WWW 进行线性运算(x×Wx \times Wx×W),得到回归结果。例如,第一行样本的回归结果为 82.4;
-
逻辑回归结果(sigmoid 转换):将回归结果通过 sigmoid 函数转换为概率值。例如,第一行样本的逻辑回归结果为 0.4;
-
预测结果:根据设定的阈值(这里阈值为 0.6),如果逻辑回归结果(概率值)大于 0.6,则预测样本属于 A 类;否则,预测属于 B 类。例如,第一行样本的逻辑回归结果为 0.4,小于 0.6,所以预测结果为 B 类;
-
真实结果:给出了样本实际所属的类别。例如,第一行样本的真实结果为 A 类,说明该预测结果不准确。
-
2.2 损失函数
-
逻辑回归的损失函数公式为:
Loss(L)=−∑i=1m(yilog(pi)+(1−yi)log(1−pi)) \text{Loss}(L) = -\sum_{i=1}^{m} \left( y_i \log(p_i) + (1 - y_i) \log(1 - p_i) \right) Loss(L)=−i=1∑m(yilog(pi)+(1−yi)log(1−pi))- 其中,pi=sigmoid(wTxi+b)p_i = \text{sigmoid}(w^T x_i + b)pi=sigmoid(wTxi+b) 是逻辑回归对第 iii 个样本的输出结果,表示样本属于正类的概率;yiy_iyi 是第 iii 个样本的真实标签(yi=1y_i = 1yi=1 表示正类,yi=0y_i = 0yi=0 表示负类);mmm 是样本的数量;
-
损失函数的工作原理:
- 对于每个样本,逻辑回归模型预测其属于 A、B 两个类别的概率;
- 损失函数的设计目的是让真实类别对应的位置上的概率值越大越好。例如,如果样本的真实类别是 A(yi=1y_i = 1yi=1),那么我们希望模型预测的属于 A 类的概率 pip_ipi 尽可能大;如果样本的真实类别是 B(yi=0y_i = 0yi=0),那么我们希望模型预测的属于 B 类的概率 1−pi1 - p_i1−pi 尽可能大;
- 通过最小化损失函数,我们可以调整模型的参数 www 和 bbb,使得模型的预测结果尽可能接近真实标签;
-
举个栗子:以图中的样本数据为例,假设真实结果中 1 表示 A 类,0 表示 B 类
-
第 1 个样本:真实结果 y1=1y_1 = 1y1=1,逻辑回归结果 p1=0.4p_1 = 0.4p1=0.4。根据损失函数公式,该样本的损失为:
y1log(p1)+(1−y1)log(1−p1)=1×log(0.4)+(1−1)×log(1−0.4)=log(0.4) y_1 \log(p_1) + (1 - y_1) \log(1 - p_1) = 1 \times \log(0.4) + (1 - 1) \times \log(1 - 0.4) = \log(0.4) y1log(p1)+(1−y1)log(1−p1)=1×log(0.4)+(1−1)×log(1−0.4)=log(0.4) -
第 2 个样本:真实结果 y2=0y_2 = 0y2=0,逻辑回归结果 p2=0.68p_2 = 0.68p2=0.68。该样本的损失为:
y2log(p2)+(1−y2)log(1−p2)=0×log(0.68)+(1−0)×log(1−0.68)=log(0.32) y_2 \log(p_2) + (1 - y_2) \log(1 - p_2) = 0 \times \log(0.68) + (1 - 0) \times \log(1 - 0.68) = \log(0.32) y2log(p2)+(1−y2)log(1−p2)=0×log(0.68)+(1−0)×log(1−0.68)=log(0.32) -
以此类推,可以计算出所有样本的损失,然后将它们求和并取负,得到总的损失值;
-
-
损失函数的概率解释
-
1 个样本的概率表示:
-
假设样本有 0、1 两个类别,某个样本被分为 1 类的概率为 ppp,则分为 0 类的概率为 1−p1 - p1−p。每一个样本分类正确的概率可以表示为:
L={pif y=11−pif y=0 L = \begin{cases} p & \text{if } y = 1 \\ 1 - p & \text{if } y = 0 \end{cases} L={p1−pif y=1if y=0 -
将其合成一个式子为:
L=py(1−p)1−y L = p^y (1 - p)^{1 - y} L=py(1−p)1−y -
我们希望当样本是 1 类别时,模型预测的 ppp 越大越好;当样本是 0 类别时,模型预测的 1−p1 - p1−p 越大越好;
-
-
n 个样本的概率表示:
-
假设有样本 [(x1,y1),(x2,y2),⋯ ,(xn,yn)][(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)][(x1,y1),(x2,y2),⋯,(xn,yn)],其中 nnn 是样本数量。所有样本都预测正确的概率为:
P=P(y1∣x1)P(y2∣x2)⋯P(yn∣xn)=∏i=1npiyi(1−pi)1−yi P = P(y_1|x_1)P(y_2|x_2) \cdots P(y_n|x_n) = \prod_{i=1}^{n} p_i^{y_i} (1 - p_i)^{1 - y_i} P=P(y1∣x1)P(y2∣x2)⋯P(yn∣xn)=i=1∏npiyi(1−pi)1−yi -
其中,pip_ipi 表示第 iii 个样本被分类正确时的概率,yiy_iyi 表示第 iii 个样本的真实类别(0 或 1);
-
-
极大似然估计:
- 问题转化为:找到合适的权重参数 www 和偏置项 bbb,使得所有样本都预测正确的联合概率 PPP 最大;
- 这就是极大似然估计的思想,即认为观测到的数据是最有可能发生的,因此需要找到使观测数据概率最大的模型参数。
-
-
损失函数的优化
-
极大似然函数转对数似然函数。为了方便计算和优化,我们对极大似然函数取对数,将连乘形式转换为对数加法形式。对数似然函数 H(L)H(L)H(L) 为:
H(L)=∑i=1m(yilog(pi)+(1−yi)log(1−pi)) H(L) = \sum_{i=1}^{m} \left( y_i \log(p_i) + (1 - y_i) \log(1 - p_i) \right) H(L)=i=1∑m(yilog(pi)+(1−yi)log(1−pi))- 其中,pi=11+e−(wTxi+b)p_i = \frac{1}{1 + e^{-(w^T x_i + b)}}pi=1+e−(wTxi+b)1 是逻辑回归的输出结果;
-
最大化问题转最小化问题。由于对数函数是单调递增的,最大化对数似然函数 H(L)H(L)H(L) 等价于最大化原似然函数。但在优化过程中,通常将最大化问题转换为最小化问题,因此我们取对数似然函数的负值,得到损失函数:
Loss(L)=−∑i=1m(yilog(pi)+(1−yi)log(1−pi)) \text{Loss}(L) = -\sum_{i=1}^{m} \left( y_i \log(p_i) + (1 - y_i) \log(1 - p_i) \right) Loss(L)=−i=1∑m(yilog(pi)+(1−yi)log(1−pi))- 这样,我们就可以通过最小化损失函数来优化模型的参数 www 和 bbb;
-
使用梯度下降优化算法。在逻辑回归中,通常使用梯度下降优化算法来更新模型的权重参数 www 和偏置项 bbb。梯度下降算法通过计算损失函数关于参数的梯度,并沿着梯度的反方向更新参数,逐步减小损失函数的值,从而找到最优的参数组合。具体的更新公式为:
w=w−α∂Loss(L)∂wb=b−α∂Loss(L)∂b w = w - \alpha \frac{\partial \text{Loss}(L)}{\partial w} \\ b = b - \alpha \frac{\partial \text{Loss}(L)}{\partial b} w=w−α∂w∂Loss(L)b=b−α∂b∂Loss(L)- 其中,α\alphaα 是学习率,控制参数更新的步长。通过不断迭代更新参数,直到损失函数收敛到最小值,此时模型的参数即为最优参数。
-
3 案例:癌症分类预测
3.1 API
-
API 函数:
sklearn.linear_model.LogisticRegression(solver='liblinear', penalty='l2', C=1.0) -
solver(损失函数优化方法)
liblinear:对于小数据集场景训练速度更快sag和saga:对于大数据集训练速度更快- 正则化支持情况:
sag、saga支持 L2 正则化或者没有正则化liblinear和saga支持 L1 正则化
-
penalty(正则化的种类):可以是
l1或者l2 -
C(正则化力度):用于控制正则化的强度,
C值越小,正则化力度越大 -
默认正例:默认将类别数量少的当做正例
3.2 案例:癌症分类预测
-
威斯康星州乳腺数据集介绍:
- 该数据包含 699 条样本,有 11 列数据;
- 首列是用于检索的样本代码编号,后 9 列是与肿瘤相关的医学特征,如细胞团厚度、细胞大小均匀性、细胞形状均匀性、边缘粘连情况、单个上皮细胞大小、裸核情况、染色质平淡程度、正常核仁情况、有丝分裂情况 ;
- 最后一列代表肿瘤类型,其中 2 表示良性,4 表示恶性,数据中存在 16 个缺失值,用 “?” 标注;
-
导包:
# 0.导包 import pandas as pd from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score import numpy as np -
加载数据并查看:
# 1.加载数据 data =pd.read_csv('data/breast-cancer-wisconsin.csv') data.info()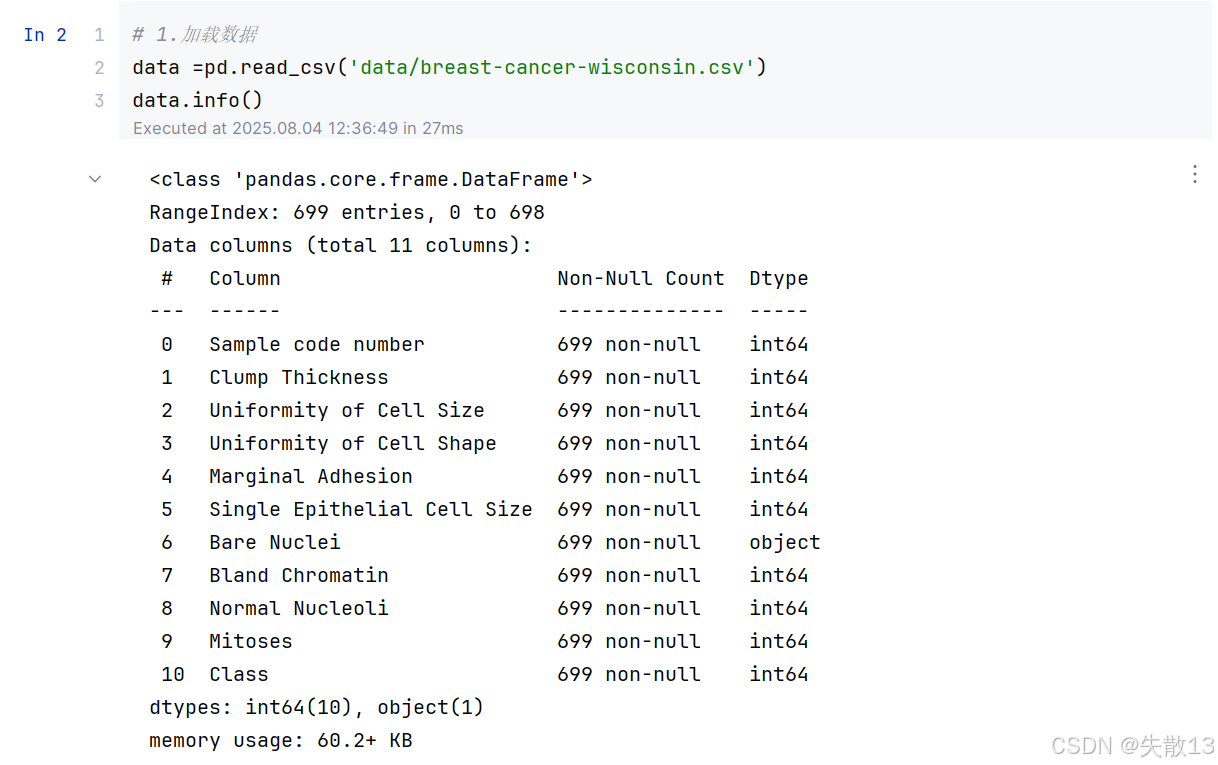
-
数据处理:
# 2.数据处理 # 2.1 处理缺失值 data =data.replace(to_replace='?',value=np.nan) data=data.dropna() # 2.2 获取特征和目标值 # 从数据中获取特征,即所有行和除了最后一列之外的所有列 X = data.iloc[:,1:-1] # 从数据中获取目标值,即'Class'列 y = data['Class'] # 2.3 数据划分,测试集占比为0.2,random_state为22以保证结果可复现 x_train,x_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=22) -
标准化:
# 3.特征工程(标准化) pre =StandardScaler() x_train=pre.fit_transform(x_train) x_test=pre.transform(x_test) -
模型训练:
# 4.模型训练 model=LogisticRegression() model.fit(x_train,y_train)
-
模型预测与评估
# 5.模型预测和评估 y_predict =model.predict(x_test) # 打印预测结果 print(y_predict) # 计算模型在测试集上的准确率 print(accuracy_score(y_test,y_predict))
4 分类问题评估
4.1 混淆矩阵
-
什么是混淆矩阵?
- 混淆矩阵是一种用于评估分类模型性能的工具,它以矩阵的形式展示了模型在预测过程中各类别的正确和错误预测情况;
- 矩阵的行表示样本的真实类别,列表示模型的预测类别;
-
混淆矩阵四个指标
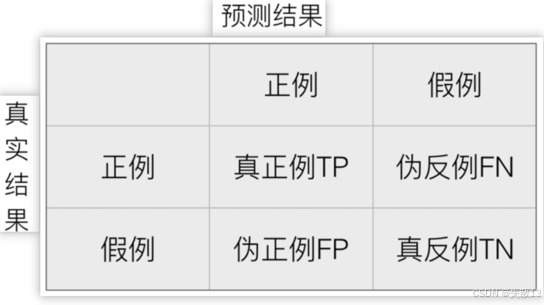
- 真正例(TP,True Positive):真实值是正例的样本中,被分类为正例的样本数量。例如,在预测肿瘤是否为恶性时,真实为恶性且被模型正确预测为恶性的样本数量;
- 伪反例(FN,False Negative):真实值是正例的样本中,被分类为假例的样本数量。例如,真实为恶性但被模型错误预测为良性的样本数量;
- 伪正例(FP,False Positive):真实值是假例的样本中,被分类为正例的样本数量。例如,真实为良性但被模型错误预测为恶性的样本数量;
- 真反例(TN,True Negative):真实值是假例的样本中,被分类为假例的样本数量。例如,真实为良性且被模型正确预测为良性的样本数量;
-
举个栗子:假设样本集有10个样本,其中6个是恶性肿瘤样本(正例),4个是良性肿瘤样本(假例)
预测正例 预测假例 真实正例:6 真实假例:4 -
模型A:预测对了3个恶性肿瘤样本,4个良性肿瘤样本
预测正例 预测假例 真实正例:6 3 真实假例:4 4 -
真正例(TP)为3:模型正确预测的恶性肿瘤样本数量
-
伪反例(FN)为3:真实为恶性但被模型错误预测为良性的样本数量(6 - 3 = 3)
预测正例 预测假例 真实正例:6 3 6 - 3 = 3 真实假例:4 4 -
伪正例(FP)为0:真实为良性但被模型错误预测为恶性的样本数量
预测正例 预测假例 真实正例:6 3 6 - 3 = 3 真实假例:4 0 4 -
真反例(TN)为4:模型正确预测的良性肿瘤样本数量
-
-
模型B:预测对了6个恶性肿瘤样本,1个良性肿瘤样本
- 真正例(TP)为6:模型正确预测的恶性肿瘤样本数量
- 伪反例(FN)为0:真实为恶性但被模型错误预测为良性的样本数量(6 - 6 = 0)
- 伪正例(FP)为3:真实为良性但被模型错误预测为恶性的样本数量(4 - 1 = 3)
- 真反例(TN)为1:模型正确预测的良性肿瘤样本数量
-
需要注意的是,TP+FN+FP+TNTP + FN + FP + TNTP+FN+FP+TN 等于总样本数量;
-
-
代码示例:
-
导包:
# 从sklearn.metrics模块中导入混淆矩阵、精确率、召回率和F1分数的计算函数 from sklearn.metrics import confusion_matrix,precision_score,recall_score,f1_score import pandas as pd -
构建数据:
# 构建数据:真实值和预测值 # 真实值列表,其中'恶性'表示正例,'良性'表示假例 y_true = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性', '良性', '良性', '良性'] # 模型A的预测值列表 y_pre_A = ['恶性', '恶性', '恶性', '良性', '良性', '良性', '良性', '良性', '良性', '良性'] # 模型B的预测值列表 y_pre_B = ['恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '恶性', '良性'] -
混淆矩阵:
# 混淆矩阵 # 计算模型A的混淆矩阵,指定标签为['恶性', '良性'] A = confusion_matrix(y_true, y_pre_A, labels=['恶性', '良性']) # 将混淆矩阵转换为DataFrame格式并打印,设置列名为['恶性', '良性'],行索引为['恶性', '良性'] print(pd.DataFrame(A, columns=['恶性', '良性'], index=['恶性', '良性']))# 计算模型B的混淆矩阵,指定标签为['恶性', '良性'] B = confusion_matrix(y_true, y_pre_B, labels=['恶性', '良性']) # 将混淆矩阵转换为DataFrame格式并打印,设置列名为['恶性', '良性'],行索引为['恶性', '良性'] print(pd.DataFrame(B, columns=['恶性', '良性'], index=['恶性', '良性']))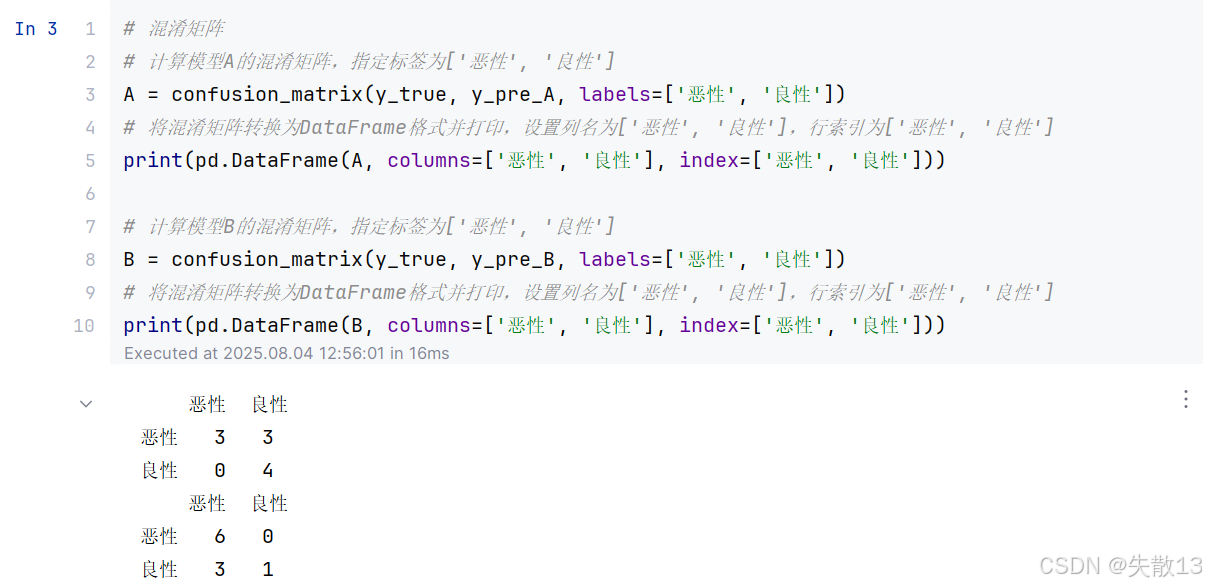
-
4.2 精确率
-
精确率(Precision):精确率也称为查准率,它衡量的是模型对正例样本的预测准确率。例如,在将恶性肿瘤视为正例样本的情况下,精确率可以告诉我们模型预测为恶性肿瘤的样本中,真正是恶性肿瘤的比例;

-
精确率的计算方法为:
P=TPTP+FP P = \frac{TP}{TP + FP} P=TP+FPTP- 其中,TPTPTP 是真正例(真实为正例且被模型正确预测为正例的样本数量),FPFPFP 是伪正例(真实为假例但被模型错误预测为正例的样本数量);
-
举个栗子:假设样本集有10个样本,其中6个是恶性肿瘤样本(正例),4个是良性肿瘤样本(假例);
-
模型A:预测对了3个恶性肿瘤样本,4个良性肿瘤样本
- 真正例(TP)为3
- 伪反例(FN)为3(6 - 3 = 3)
- 伪正例(FP)为0
- 真反例(TN)为4
- 精确率为:
PA=33+0=100% P_A = \frac{3}{3 + 0} = 100\% PA=3+03=100%
-
模型B:预测对了6个恶性肿瘤样本,1个良性肿瘤样本。
- 真正例(TP)为6
- 伪反例(FN)为0(6 - 6 = 0)
- 伪正例(FP)为3(4 - 1 = 3)
- 真反例(TN)为1
- 精确率为:
PB=66+3≈67% P_B = \frac{6}{6 + 3} \approx 67\% PB=6+36≈67%
-
-
代码示例:
# 计算模型A的精确率,指定正例标签为'恶性' print(precision_score(y_true, y_pre_A, pos_label='恶性')) # 计算模型B的精确率,指定正例标签为'恶性' print(precision_score(y_true, y_pre_B, pos_label='恶性'))
4.3 召回率
-
召回率(Recall):召回率也称为查全率,它指的是预测为正例样本占所有真实正例样本的比重。例如,在将恶性肿瘤视为正例样本的情况下,召回率可以告诉我们模型能够正确预测出的恶性肿瘤患者在所有实际恶性肿瘤患者中所占的比例;

-
召回率的计算方法为:
R=TPTP+FN R = \frac{TP}{TP + FN} R=TP+FNTP- 其中,TPTPTP 是真正例(真实为正例且被模型正确预测为正例的样本数量),FNFNFN 是伪反例(真实为正例但被模型错误预测为假例的样本数量);
-
举个栗子:假设样本集有10个样本,其中6个是恶性肿瘤样本(正例),4个是良性肿瘤样本(假例)
-
模型A:预测对了3个恶性肿瘤样本,4个良性肿瘤样本。
- 真正例(TP)为3。
- 伪反例(FN)为3(6 - 3 = 3)。
- 伪正例(FP)为0。
- 真反例(TN)为4。
- 召回率为:
RA=33+3=50% R_A = \frac{3}{3 + 3} = 50\% RA=3+33=50%
-
模型B:预测对了6个恶性肿瘤样本,1个良性肿瘤样本。
- 真正例(TP)为6。
- 伪反例(FN)为0(6 - 6 = 0)。
- 伪正例(FP)为3(4 - 1 = 3)。
- 真反例(TN)为1。
- 召回率为:
RB=66+0=100% R_B = \frac{6}{6 + 0} = 100\% RB=6+06=100%
-
-
代码示例
# 计算模型A的召回率,指定正例标签为'恶性' print(recall_score(y_true, y_pre_A, pos_label='恶性')) # 计算模型B的召回率,指定正例标签为'恶性' print(recall_score(y_true, y_pre_B, pos_label='恶性'))
4.4 F1-score
-
F1-score:F1-score 是精确率(Precision)和召回率(Recall)的调和平均值,用于综合评估模型在精确率和召回率两个方面的性能。当我们对模型的精确率和召回率都有要求,希望了解模型在这两个评估方向的综合预测能力时,可以使用 F1-score;
-
F1-score 的计算方法为:
F1=2×Precision×RecallPrecision+Recall F1 = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} F1=Precision+Recall2×Precision×Recall -
举个栗子:假设样本集有10个样本,其中6个是恶性肿瘤样本(正例),4个是良性肿瘤样本(假例)
-
模型A:
- 精确率(Precision)为100%
- 召回率(Recall)为50%
- F1-score 为
F1A=2×100%×50%100%+50%≈67% F1_A = \frac{2 \times 100\% \times 50\%}{100\% + 50\%} \approx 67\% F1A=100%+50%2×100%×50%≈67%
-
模型B:
- 精确率(Precision)为67%
- 召回率(Recall)为100%
- F1-score 为:
F1B=2×67%×100%67%+100%≈80% F1_B = \frac{2 \times 67\% \times 100\%}{67\% + 100\%} \approx 80\% F1B=67%+100%2×67%×100%≈80%
-
-
代码示例
# 计算模型A的F1-score,指定正例标签为'恶性' print(f1_score(y_true, y_pre_A, pos_label='恶性')) # 计算模型B的F1-score,指定正例标签为'恶性' print(f1_score(y_true, y_pre_B, pos_label='恶性'))
4.5 AUC指标&ROC曲线
-
真正率(TPR)与假正率(FPR)
-
真正率(TPR,True Positive Rate):正样本中被预测为正样本的概率。它衡量的是模型对正样本的识别能力;
-
假正率(FPR,False Positive Rate):负样本中被预测为正样本的概率。它衡量的是模型将负样本错误分类为正样本的概率;
-
通过这两个指标,可以描述模型对正、负样本的分辨能力;
-
-
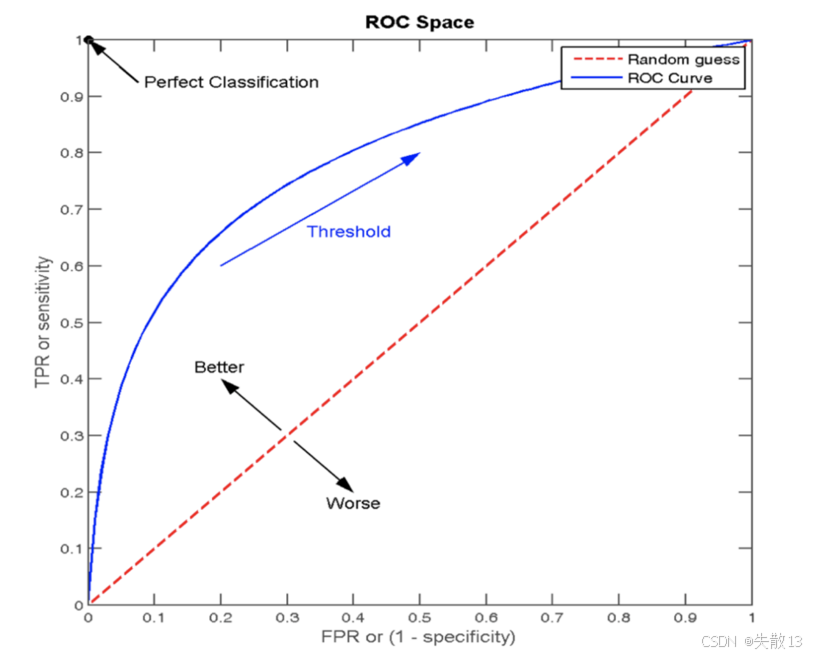
ROC曲线(Receiver Operating Characteristic curve):ROC曲线是一种常用于评估分类模型性能的可视化工具。它以模型的真正率(TPR)为纵轴,假正率(FPR)为横轴,将模型在不同阈值下的表现以曲线的形式展现出来;
-
AUC(Area Under the ROC Curve)指标,即ROC曲线下面积:ROC曲线的优劣可以通过曲线下的面积(AUC)来衡量,AUC越大表示分类器性能越好;
-
当 AUC=0.5AUC = 0.5AUC=0.5 时,表示分类器的性能等同于随机猜测;
-
当 AUC=1AUC = 1AUC=1 时,表示分类器的性能完美,能够完全正确地将正负例分类;
-
-
ROC 曲线图像中,4 个特殊点的含义:ROC曲线图像中,x轴表示FPR,y轴表示TPR,任意一点的坐标为(FPR值,TPR值);
- 点 (0, 0):所有的负样本都预测正确,所有的正样本都预测为错误;
- 点 (1, 0):所有的负样本都预测错误,所有的正样本都预测错误。这是最不好的效果;
- 点 (1, 1):所有的负样本都预测错误,表示所有的正样本都预测正确;
- 点 (0, 1):所有的负样本都预测正确,表示所有的正样本都预测正确。这是最好的效果;
- ROC曲线上的每个点代表模型在不同阈值下的性能表现。从图像上来看,曲线越靠近 (0,1)(0, 1)(0,1) 点则模型对正负样本的辨别能力就越强;
-
案例:ROC 曲线的绘制
-
已知在网页某个位置有一个广告图片,该广告共被展示了6次,有2次被浏览者点击了。每次点击的概率见下图,其中正样本为 {1,3}\{1, 3\}{1,3},负样本为 {2,4,5,6}\{2, 4, 5, 6\}{2,4,5,6}。要求画出在不同阈值下的ROC曲线;
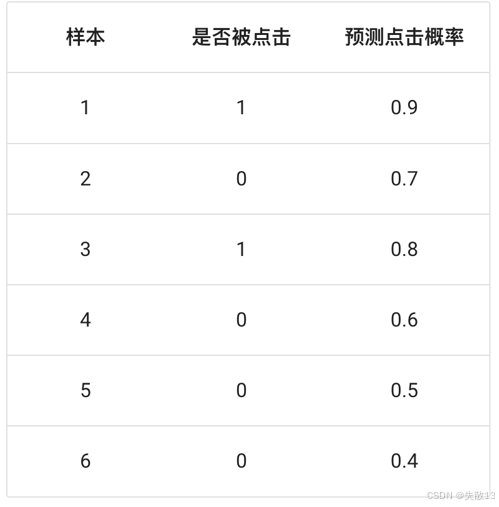
-
思路分析:根据不同的阈值,求出TPR和FPR,得出点坐标画ROC图;
-
不同阈值下的计算:
-
阈值:0.9
- 原本为正例的1、3号样本中3号样本被分类错误,则 TPR=0/2=0TPR = 0/2 = 0TPR=0/2=0
- 原本为负例的2、4、5、6号样本没有一个被分为正例,则 FPR=0FPR = 0FPR=0
-
阈值:0.8
- 原本为正例的1、3号样本被分类正确,则 TPR=1/2=0.5TPR = 1/2 = 0.5TPR=1/2=0.5
- 原本为负例的2、4、5、6号样本没有一个被分为正例,则 FPR=0FPR = 0FPR=0
-
阈值:0.7
- 原本为正例的1、3号样本被分类正确,则 TPR=2/2=1TPR = 2/2 = 1TPR=2/2=1
- 原本为负类的2、4、5、6号样本中2号样本被分类错误,则 FPR=0/4=0FPR = 0/4 = 0FPR=0/4=0
-
阈值:0.6
- 原本为正例的1、3号样本被分类正确,则 TPR=2/2=1TPR = 2/2 = 1TPR=2/2=1
- 原本为负类的2、4、5、6号样本中2、4号样本被分类错误,则 FPR=1/4=0.25FPR = 1/4 = 0.25FPR=1/4=0.25
-
阈值:0.5
- 原本为正例的1、3号样本被分类正确,则 TPR=2/2=1TPR = 2/2 = 1TPR=2/2=1
- 原本为负类的2、4、5、6号样本中2、4、5号样本被分类错误,则 FPR=2/4=0.5FPR = 2/4 = 0.5FPR=2/4=0.5
-
阈值:0.4
- 原本为正例的1、3号样本被分类正确,则 TPR=2/2=1TPR = 2/2 = 1TPR=2/2=1
- 原本为负类的2、4、5、6号样本全部被分类错误,则 FPR=3/4=0.75FPR = 3/4 = 0.75FPR=3/4=0.75
-
-
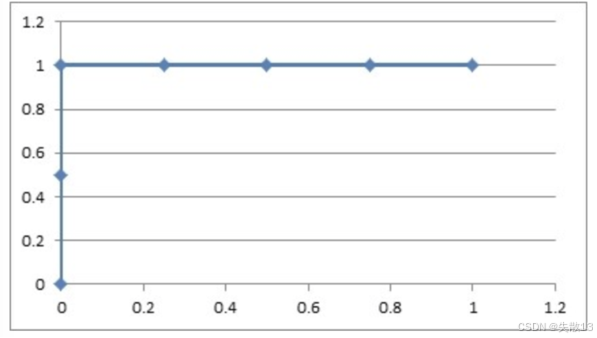
不同阈值下的点坐标:(0,0.5)(0, 0.5)(0,0.5)、(0,1)(0, 1)(0,1)、(0.25,1)(0.25, 1)(0.25,1)、(0.5,1)(0.5, 1)(0.5,1)、(0.75,1)(0.75, 1)(0.75,1)、(1,1)(1, 1)(1,1);
-
由 TPR 和 FPR 构成的 ROC 图像中,ROC曲线上的每个点代表模型在不同阈值下的性能表现;
-
-
AUC的计算 API:
from sklearn.metrics import roc_auc_score sklearn.metrics.roc_auc_score(y_true, y_score)-
功能:计算 ROC 曲线面积,即 AUC 值
-
参数:
y_true:每个样本的真实类别,必须为 0(反例)、1(正例)标记y_score:预测得分,可以是正例的估计概率、置信值或者分类器方法的返回值
-
-
分类评估报告 API:
sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None)-
参数:
y_true:真实目标值y_pred:估计器预测目标值labels:指定类别对应的数字target_names:目标类别名称
-
返回值:每个类别精确率与召回率;
-
5 案例:电信客户流失预测
5.1 概述
-
案例需求:通过分析用户的个人信息、通话及上网数据,确定影响客户流失的关键因素,构建预测模型判断用户是否会流失,并提出预警策略;
-
数据集概况:
- 包含 7043 条样本,16 列数据,内存占用约 880.5KB;
- 数据类型:2 列浮点型(
MonthlyCharges、TotalCharges)、12 列整数型、2 列对象型(Churn、gender); - 无缺失值,数据完整性较好;
-
字段含义说明:
字段名称 含义说明 Churn客户是否流失(目标变量, Yes表示流失,No表示未流失)gender客户性别( Male男性、Female女性)Partner_att配偶是否为 ATT 用户(1 是,0 否) Dependents_att家人是否为 ATT 用户(1 是,0 否) landline是否使用 ATT 固话服务(1 是,0 否) internet_att是否使用 ATT 互联网服务(1 是,0 否) internet_other是否使用其他运营商互联网服务(1 是,0 否) StreamingTV是否使用在线电视服务(1 是,0 否) StreamingMovies是否使用在线电影服务(1 是,0 否) Contract_Month是否为月度合约用户(1 是,0 否) Contract_1YR是否为年度合约用户(1 是,0 否) PaymentBank是否使用银行付款(1 是,0 否) PaymentCreditcard是否使用信用卡付款(1 是,0 否) PaymentElectronic是否使用电子付款(1 是,0 否) MonthlyCharges每月话费(浮点型,数值) TotalCharges累计话费(浮点型,数值) -
案例步骤分析:
- 数据基本处理
- 查看数据行 / 列数量:了解数据集的规模,包括样本数量和特征数量;
- 对类别数据进行 one-hot 处理:将类别型特征转换为数值型特征,以便模型能够处理。例如,将性别(男、女)转换为两个二进制特征(是否为男、是否为女);
- 查看标签分布情况:了解目标变量(客户是否流失)的分布情况,判断数据是否平衡。如果数据不平衡,可能需要进行采样或调整模型参数;
- 特征筛选
- 分析哪些特征对标签值影响大:通过统计方法或机器学习模型,分析各个特征与目标变量之间的相关性或重要性;
- 对标签进行分组统计,对比 0/1 标签分组后的均值等:将数据按照目标变量的不同取值(0 表示未流失,1 表示流失)进行分组,计算各个特征在不同组内的均值、方差等统计量,以发现特征与目标变量之间的关系;
- 初步筛选出对标签影响比较大的特征,形成 x、y:根据特征分析的结果,选择对目标变量影响较大的特征作为模型的输入(x),目标变量作为输出(y);
- 模型训练
- 样本均衡情况下模型训练:如果数据集中目标变量的分布比较均衡,可以直接使用原始数据进行模型训练;
- 样本不平衡情况下模型训练:如果数据集中目标变量的分布不平衡(例如,流失客户的比例远低于未流失客户的比例),可以采用过采样、欠采样或合成新样本等方法来平衡数据,然后再进行模型训练;
- 交叉验证网格搜索等方式模型训练:为了提高模型的泛化能力,可以采用交叉验证的方法来评估模型的性能,并通过网格搜索等方式来优化模型的超参数;
- 模型评估
- 精确率:衡量模型预测为正例的样本中,真正是正例的比例;
- Roc_AUC 指标计算:ROC 曲线下的面积(AUC)是评估二分类模型性能的常用指标,AUC 值越大表示模型的性能越好。
- 数据基本处理
5.2 代码
-
导包:
# 0.导包 import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score,roc_auc_score,classification_report -
数据处理:
# 1.数据处理 data =pd.read_csv('data/churn.csv') print(data.info()) print(data.head())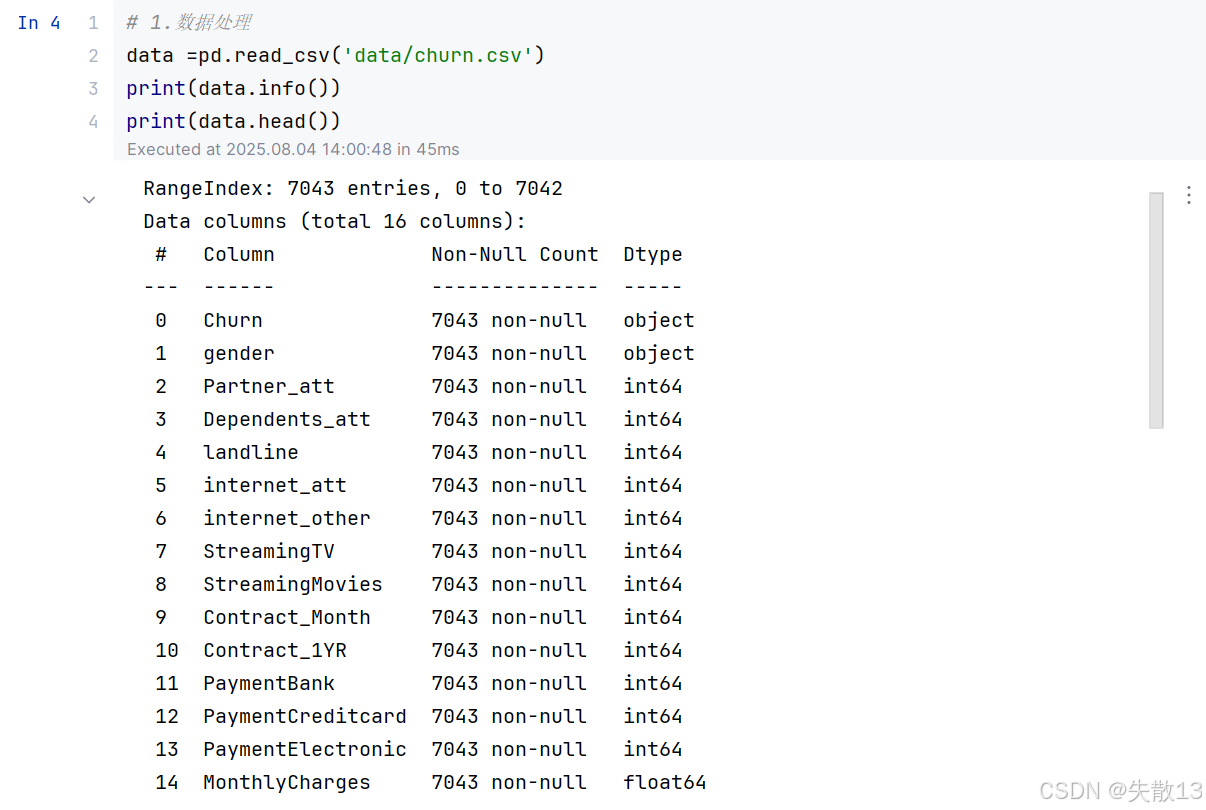
# 对类别型特征进行 one-hot 编码 data =pd.get_dummies(data) print(data.head())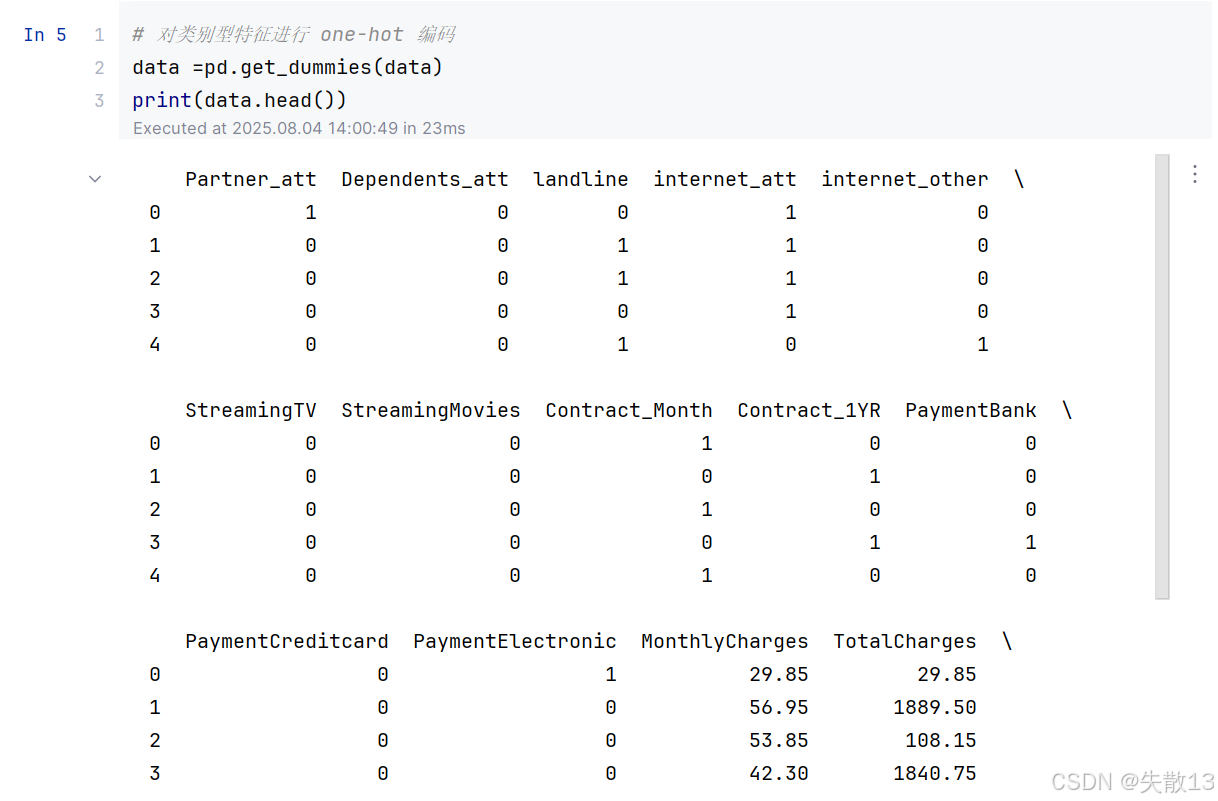
# 删除指定的列('Churn_No' 和 'gender_Male') data = data.drop(['Churn_No','gender_Male'],axis=1) print(data.head())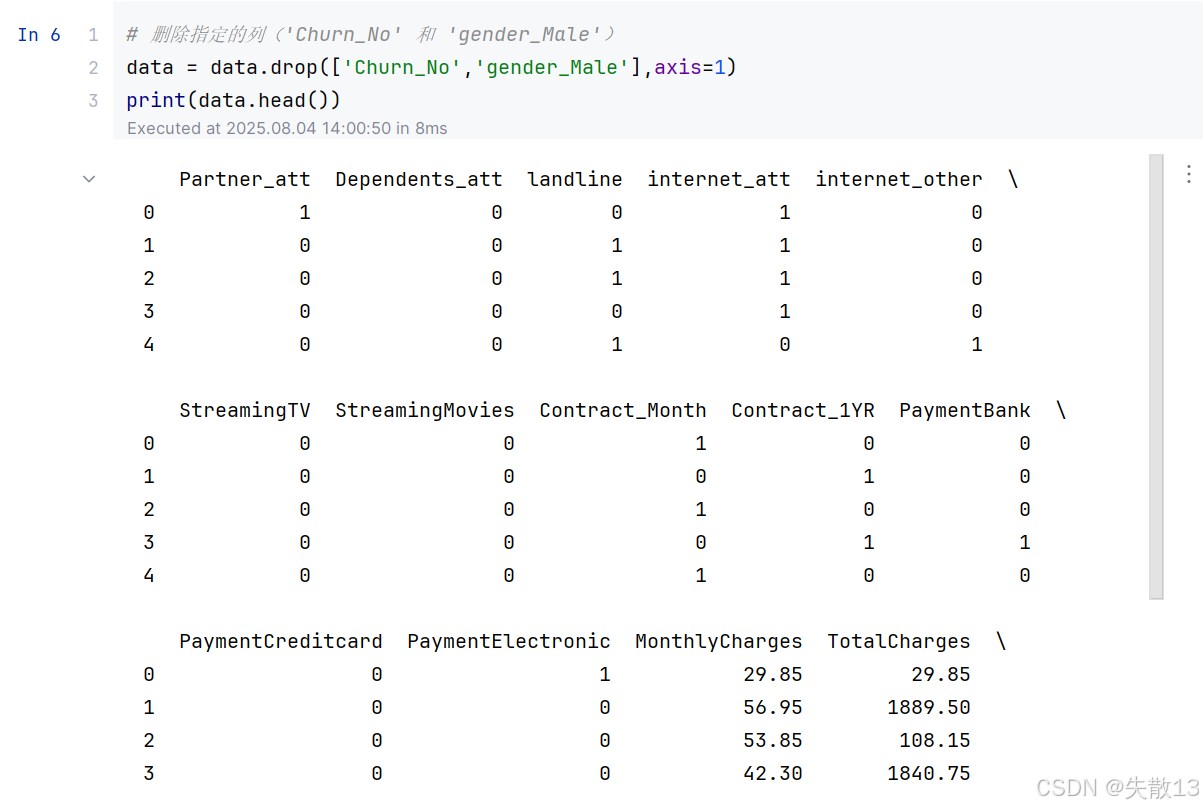
# 将 'Churn_Yes' 列重命名为 'flag' data = data.rename(columns = {'Churn_Yes':'flag'}) print(data.head()) # 查看 'flag' 列的取值分布情况 print(data.flag.value_counts())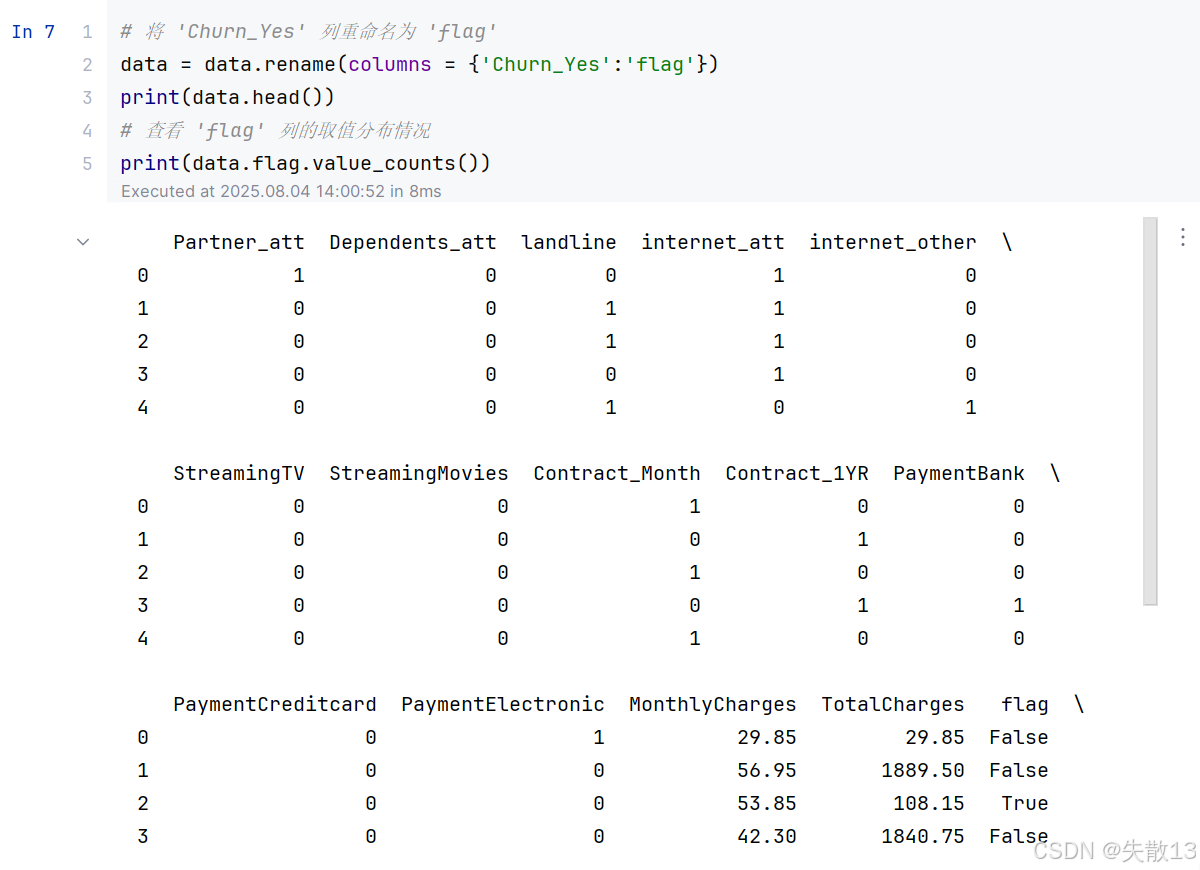
-
特征工程:
# 2.特征工程 # 绘制 'Contract_Month' 特征在不同 'flag' 取值下的计数图 sns.countplot(data=data,y = 'Contract_Month',hue='flag') plt.show() # 选择特征列('PaymentElectronic'、'Contract_Month'、'internet_other')作为输入 x x = data[['PaymentElectronic','Contract_Month','internet_other']] # 选择 'flag' 列作为输出 y y = data['flag'] # 将数据划分为训练集和测试集,测试集占比为 0.2,stratify=y 保证分层抽样,random_state=22 保证结果可复现 x_train,x_test,y_train,y_test =train_test_split(x,y,stratify=y,test_size=0.2,random_state=22)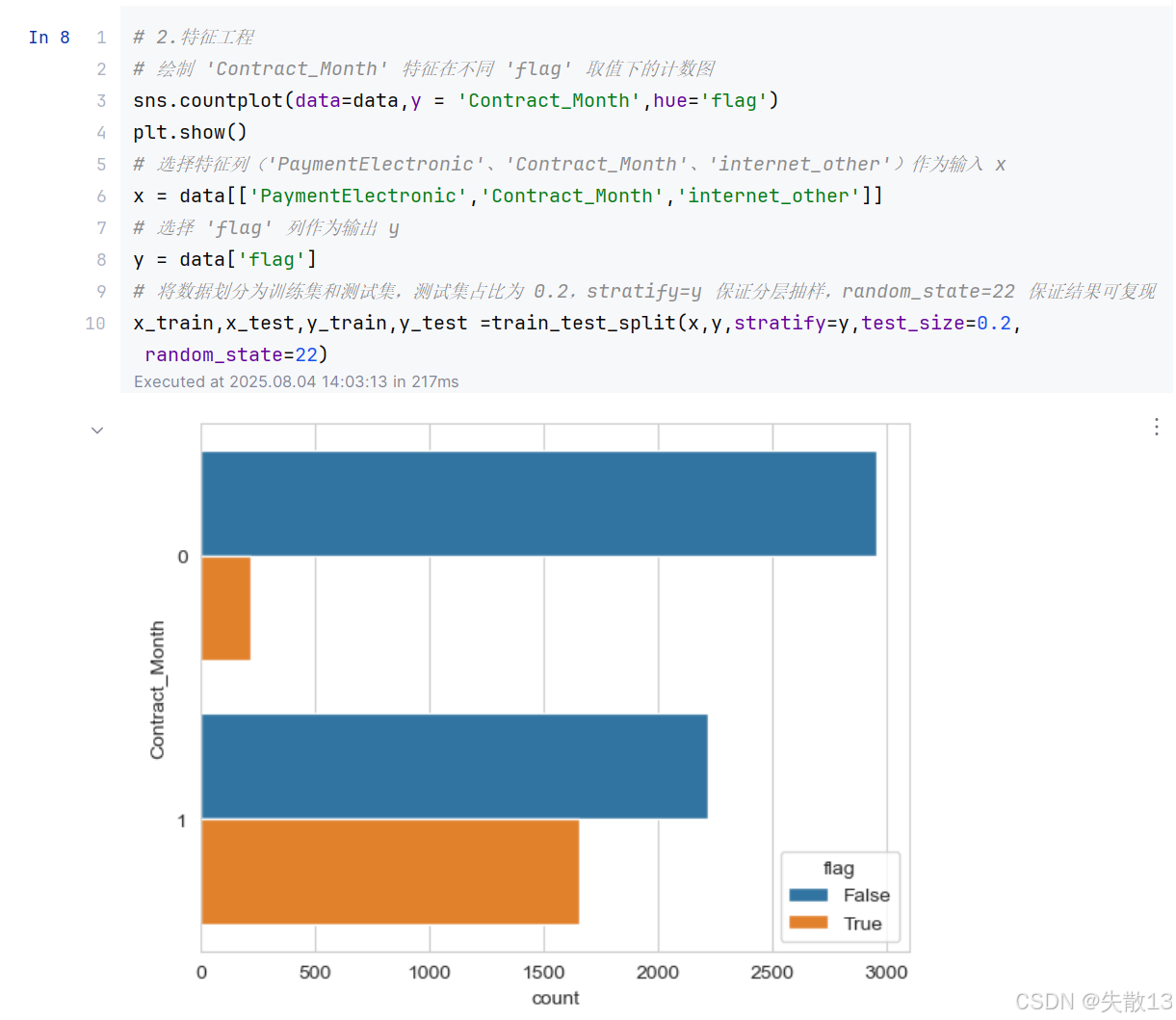
-
模型训练:
# 3.模型训练 LR =LogisticRegression() LR.fit(x_train,y_train)
-
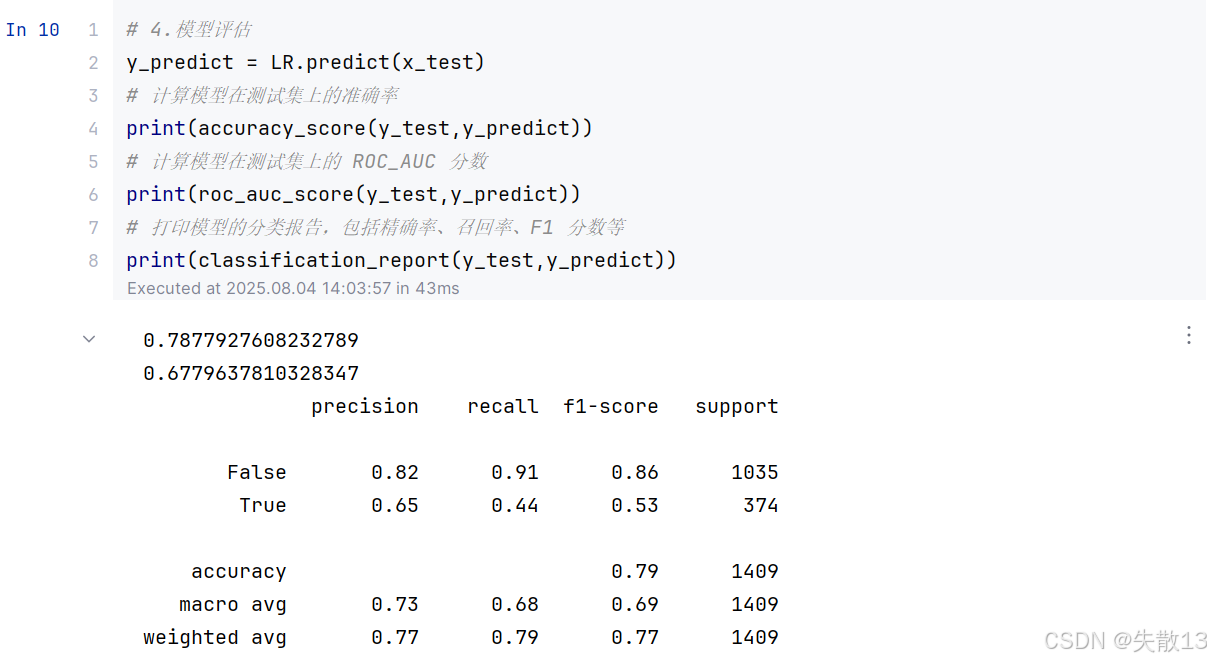
模型评估:
# 4.模型评估 y_predict = LR.predict(x_test) # 计算模型在测试集上的准确率 print(accuracy_score(y_test,y_predict)) # 计算模型在测试集上的 ROC_AUC 分数 print(roc_auc_score(y_test,y_predict)) # 打印模型的分类报告,包括精确率、召回率、F1 分数等 print(classification_report(y_test,y_predict))