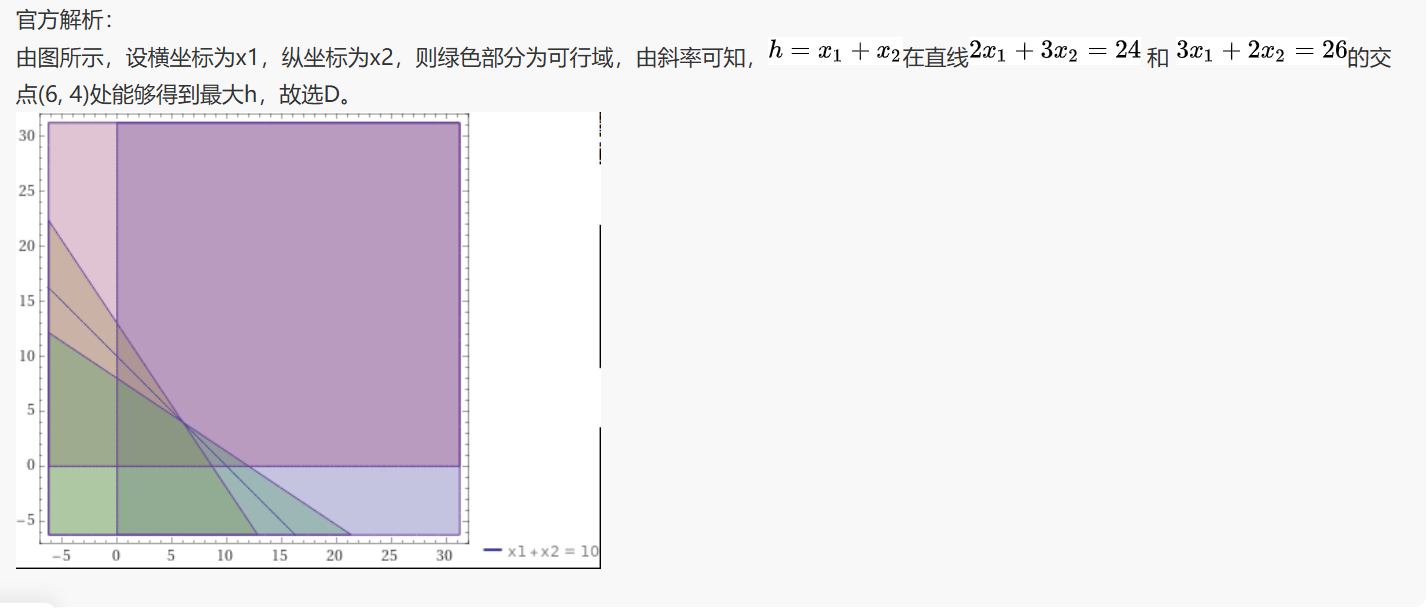
线性规划最优解

解题步骤

线性规划问题的最优解通常出现在可行域的顶点上。因此，我们可以通过求解约束条件的交点来找到这些顶点，然后计算目标函数在这些顶点的值，从而确定最优解。

第一步：绘制约束条件

1. 约束条件 2x1​+3x2​≤24：

   • 等式形式：2x1​+3x2​=24
   • 当 x1​=0，x2​=8；当 x2​=0，x1​=12。
   • 连接点 (0,8) 和 (12,0)。

2. 约束条件 3x1​+2x2​≤26：

   • 等式形式：3x1​+2x2​=26
   • 当 x1​=0，x2​=13；当 x2​=0，x1​=326​≈8.67。
   • 连接点 (0,13) 和 (26​/3,0)。

3. 非负约束：x1​≥0，x2​≥0，限制解在第一象限。

---

第二步：求约束条件的交点

我们需要求解以下两个约束的交点：

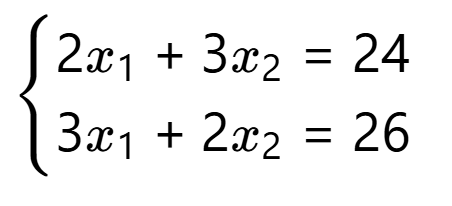
用消元法求解：

1. 将第一式乘以 3，第二式乘以 2：

   

2. 两式相减：

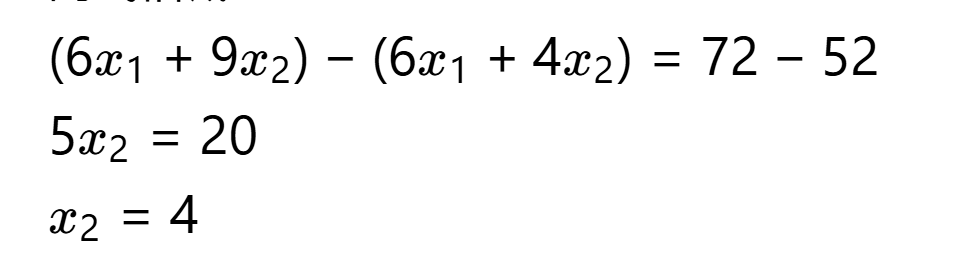
3. 将 x2​=4 代入第一式：

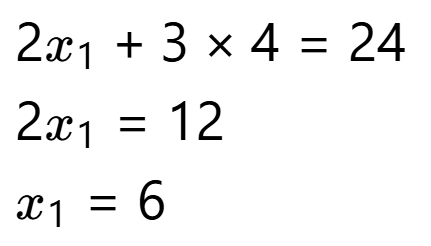
因此，交点为 (6,4)。

---

第三步：确定可行域的顶点

可行域的顶点包括：

1. (0,0)：两个约束和非负约束的交点。
2. (0,8)：2x1​+3x2​=24 与 x1​=0 的交点。
   • 检查是否满足 3x1​+2x2​≤26：3×0+2×8=16≤26，满足。
3. (6,4)：两个约束的交点。
4. (26/3​,0)：3x1​+2x2​=26 与 x2​=0 的交点。
   • 检查是否满足 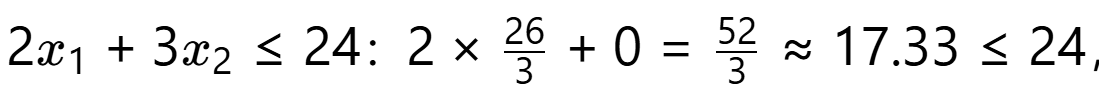，满足。

---

第四步：计算目标函数在各顶点的值

计算 f=x1​+x2​：

1. (0,0)：f=0+0=0
2. (0,8)：f=0+8=8
3. (6,4)：f=6+4=10
4. (26/3​,0)：f=326​+0≈8.67

---

第五步：确定最优值

比较以上结果，最大的 f 值为 10，对应的点是 (6,4)。

验证

验证 (6,4) 是否满足所有约束：

1. 2×6+3×4=12+12=24≤24，满足。
2. 3×6+2×4=18+8=26≤26，满足。
3. x1​=6≥0，x2​=4≥0，满足。

结论

该线性规划问题的最优值为 ​10，在点 (6,4) 处取得。