CMU-15445(7)——PROJECT#2-BPlusTree-Task#2Task#3

Task #2 - B+Tree Operations

Task2 的目的是实现 B+ 树的插入、删除和查询操作，相比 TASK#1 来说难了很多，是 PROJECT#2 的核心。

需要修改的文件：

• src/include/storage/index/b_plus_tree.h
• src/storage/index/b_plus_tree.cpp

参考：

B+ Tree Visualization

CMU15445 (Fall 2020) 数据库系统 Project#2 - B+ Tree 详解（上篇） - 之一Yo - 博客园

做个数据库：2022 CMU15-445 Project2 B+Tree Index - 知乎

B树和B+树的插入、删除图文详解 - nullzx - 博客园（可以着重学习理解）

b_plus_tree.h 中的 Context 类是 B + 树操作的上下文管理器，主要用来跟踪B+树操作过程中访问的页面。

BPlusTree 类是 TASK2 的核心类，主要负责 B+ 树节点的插入、删除和查询。先分析一下其成员变量的作用：

std::string index_name_;          // 索引名称
BufferPoolManager *bpm_;          
KeyComparator comparator_;         // 键比较器，
std::vector<std::string> log;     // 日志
int leaf_max_size_;                // 叶子节点最大键数
int internal_max_size_;            // 内部节点最大键数
page_id_t header_page_id_;         // 头部页面ID

• index_name_ 是索引名称，类比 MYSQL 中的 CREATE INDEX、DROP INDEX
• comparator_ 是 B+ 树节点值的比较函数，在 src/include/storage/index/generic_key.h 中已定义了比较函数 GenericComparator，可以自行查看
• header_page_id_ 是根页面 id，仅仅用来检索根页面，防止并发环境下可能出现的竞态条件。src/include/storage/page/b_plus_tree_header_page.h 的实现也很简单，仅有一个成员变量 page_id_t root_page_id_

方法根据功能可分为四类：

1. 状态查询

   auto IsEmpty() const -> bool;  // 判断B+树是否为空
   auto GetRootPageId() -> page_id_t;  // 获取根页面ID
   

2. 数据操作

   auto Insert(const KeyType &key, const ValueType &value) -> bool;  // 插入键值对
   void Remove(const KeyType &key);  // 删除指定键
   auto GetValue(const KeyType &key, std::vector<ValueType> *result) -> bool;  // 查询键对应的值
   

3. 迭代器接口

   auto Begin() -> INDEXITERATOR_TYPE;  // 返回第一个键值对的迭代器
   auto End() -> INDEXITERATOR_TYPE;    // 返回末尾迭代器
   auto Begin(const KeyType &key) -> INDEXITERATOR_TYPE;  // 返回大于等于指定键的迭代器
   

4. 辅助工具函数

   void Print(BufferPoolManager *bpm);  // 打印树结构
   void Draw(BufferPoolManager *bpm, const std::filesystem::path &outf);  // 绘制树结构到文件
   auto DrawBPlusTree() -> std::string;  // 返回树结构的字符串表示
   

我们需要实现前三部分，辅助工具已实现我们只需调试调用即可。

B+树操作原理

参考B树和B+树的插入、删除图文详解 - nullzx - 博客园

必要函数实现

IsEmpty() 的实现很简单，获取 header_page_id_ 对应的 ReadPageGuard 后，通过 As 方法转换为 BPlusTreeHeaderPage，判断其 root_page_id_ 是否等于 INVALID_PAGE_ID。

B+ Tree 查找

B+ Tree 的查找比较简单，先从根节点开始，将内部节点与搜索的 key 进行二分搜索，找出包含 key 的子节点的指针，然后向缓冲池要子节点页，接着在子节点上重复上述过程直到叶节点为止，最后在叶节点上进行二分搜索。

首先实现辅助函数 KeyBinarySearch ：

INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::KeyBinarySearch(const BPlusTreePage *page, const KeyType &key) -> int {// 叶子节点if (page->IsLeafPage()) {const auto *leaf = static_cast<const LeafPage *>(page);int l = 0, r = leaf->GetSize() - 1;while (l <= r) {int mid = l + (r - l) / 2;int cmp = comparator_(key, leaf->KeyAt(mid));if (cmp == 0) return mid;cmp < 0 ? (r = mid - 1) : (l = mid + 1);}return -1;}const auto *inner = static_cast<const InternalPage *>(page);int l = 1, r = inner->GetSize() - 1;// 内部节点的一个特殊情况，考虑key小于结点中第一个键的情况if (comparator_(key, inner->KeyAt(l)) < 0) return 0;while (l <= r) {int mid = l + (r - l) / 2;int cmp = comparator_(inner->KeyAt(mid), key);if (cmp <= 0) {if (mid == r || comparator_(inner->KeyAt(mid + 1), key) > 0) return mid;l = mid + 1;} else {r = mid - 1;}}return inner->GetSize() - 1;
}

该函数用于在 B+ 树的节点中查找指定的键，对于叶子节点找到匹配键时返回对应索引；对于内部节点返回导航到子节点的索引。

需要将函数写为两部分，第一部分用于查找叶子节点匹配键对应的索引，用常规的二分法就行，网上有很多教程不过多介绍。

因为内部节点不存储实际数据，而是存储 “索引键 + 子节点指针”，用于导航到下一层节点，其键按升序排列，且首个位置（index=0）不存储键（仅存储子节点指针），因此第二部分键从 index=1 开始，如下图所示：

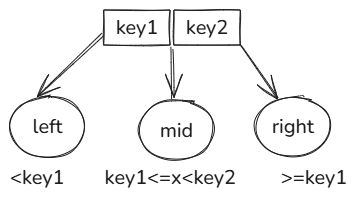
对于目标键 key，它应该进入的子节点指针为：

• 若 key < k1 → 选 p0；
• 若 k1 ≤ key < k2 → 选 p1；
• 若 k2 ≤ key < k3 → 选 p2；
• 若 key ≥ k3 → 选 p3；

因此第二部分的主要作用是在内部节点的键中，找到 “最大的且小于等于 key 的键” 的索引，这个索引对应的子节点就是 key 应该进入的下一层节点。

假设内部节点的索引键为 [*, 20, 40, 60]，子节点指针为 [p0, p1, p2, p3]，我们要查找 key=25。

• 第一次循环：l=1, r=3，mid=2（键 = 40）
  cmp=40>25 → 进入 else，r=mid-1=1
• 第二次循环：l=1, r=1，mid=1（键 = 20）
  cmp=20<=25 → 进入 if
  检查 mid+1=2 是否 > r=1？不，mid+1=2 <=1 为假
  再检查 KeyAt(mid+1)=40 与 key=25 的比较：40>25 → 条件满足
  因此 return mid=1
• 返回索引 1，对应子节点指针 p1（符合导航规则：20 ≤ 25 <40 → 选 p1）

利用实现的辅助函数 KeyBinarySearch 实现 GetValue，需要注意的是，通过 ctx.read_set_.push_back(bpm_->ReadPage(page_id)) 获取读页后，在读取完需要释放 ctx.read_set_.pop_front()。

B+ Tree 插入

先实现辅助函数 IndexBinarySearchLeaf:

INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::IndexBinarySearchLeaf(LeafPage *page, const KeyType &key) -> int {int l = 0, r = page->GetSize() - 1;int size = page->GetSize();if (comparator_(key, page->KeyAt(l)) < 0) {return 0;}while (l <= r) {int mid = (l + r) >> 1;if (comparator_(page->KeyAt(mid), key) < 0) {if (mid + 1 >= size || comparator_(page->KeyAt(mid + 1), key) >= 0) {return mid + 1;}l = mid + 1;} else {r = mid - 1;}}return -1;
}

该函数主要用来辅助 insert 函数查找目标 key 要在叶子节点中插入的位置。

B+ 树的插入较为复杂，由于 B+ 树需要保持平衡和有序性，插入过程不仅要完成键值对的存储，还要处理节点满时的分裂、并发控制（以及根节点更新等逻辑，可以在这个算法可视化网站查看 B+ 树的插入过程。

总体流程为 “初始化与空树处理”→“乐观锁尝试插入”→“悲观锁强制插入（含分裂）” 三大部分。

第一部分判断是否为空树，如果是，则可以直接插入作为根节点。

第二部分先假设插入可以在不触发节点分裂的情况下完成，以最小的锁开销尝试插入。主要流程为：

// 乐观锁：先以读锁定位叶子节点，尝试升级为写锁后插入
BPlusTreePage *op_write_page = nullptr;
ctx.read_set_.push_back(bpm_->ReadPage(ctx.root_page_id_));  // 根节点加读锁
auto op_page = ctx.read_set_.back().As<BPlusTreePage>();// 若根节点是叶子节点，直接升级为写锁
if (op_page->IsLeafPage()) {ctx.read_set_.pop_back();ctx.write_set_.push_back(bpm_->WritePage(ctx.root_page_id_));  // 升级为写锁op_page = ctx.write_set_.back().As<BPlusTreePage>();
}
ctx.header_page_ = std::nullopt;  // 释放头页面锁（已获取根节点ID）// 逐层导航到叶子节点（读锁模式）
page_id_t page_id = ctx.root_page_id_;
while (!op_page->IsLeafPage()) {int index = KeyBinarySearch(op_page, key);  // 内部节点中查找子节点索引if (index == -1) return false;  // 键不存在于树中（无需插入）auto internal_page = static_cast<const InternalPage *>(op_page);page_id = internal_page->ValueAt(index);  // 获取子节点IDctx.read_set_.push_back(bpm_->ReadPage(page_id));  // 子节点加读锁op_page = ctx.read_set_.back().As<BPlusTreePage>();// 若到达叶子节点，升级为写锁if (op_page->IsLeafPage()) {ctx.read_set_.pop_back();ctx.write_set_.push_back(bpm_->WritePage(page_id));  // 升级为写锁op_page = ctx.write_set_.back().As<BPlusTreePage>();}ctx.read_set_.pop_front();  // 释放上层节点读锁（减少竞争）
}// 尝试在叶子节点插入（若节点未满）
op_write_page = ctx.write_set_.back().AsMut<BPlusTreePage>();
if (op_write_page->GetSize() < op_write_page->GetMaxSize()) {auto leaf_page = static_cast<LeafPage *>(op_write_page);int insert_index = IndexBinarySearchLeaf(leaf_page, key);  // 找插入位置// 检查是否重复键（B+树要求键唯一）if (insert_index == -1 || comparator_(leaf_page->KeyAt(insert_index), key) == 0) {return false;}// 移动现有键，腾出插入位置int size = leaf_page->GetSize();for (int i = size; i > insert_index; i--) {leaf_page->SetKeyAt(i, leaf_page->KeyAt(i - 1));leaf_page->SetValueAt(i, leaf_page->ValueAt(i - 1));}// 插入新键值对并更新节点大小leaf_page->SetKeyAt(insert_index, key);leaf_page->SetValueAt(insert_index, value);leaf_page->SetSize(size + 1);return true;
}// 若叶子节点已满，释放乐观锁，切换到悲观锁
ctx.write_set_.clear();

1. 以读锁导航至叶子节点（从根节点开始，通过KeyBinarySearch查找子节点索引）
2. 到达叶子节点后，将读锁升级为写锁
3. 检查叶子节点是否未满：
   • 若未满：通过IndexBinarySearchLeaf找到插入位置，移动现有键值对腾出空间，插入新键值对
   • 若已满：释放当前锁，切换到悲观锁流程

第三部分仅当叶子节点已满时，通过悲观锁处理节点分裂，而且需要递归更新上层节点，主要流程和乐观锁差不多，都是先找叶子节点然后再插入，区别在于：

1. 导航叶子节点的过程中全程持写锁
2. 叶子节点若满，则需要分裂，并且更新 B + 树索引头页中的 root_page_id

全程写锁简单，将 bpm_->WritePage 换成 bpm_->WritePage 就行。但是分裂很复杂，不仅需要分裂节点，而且需要递归更新上层节点。分裂的完整过程分为**“叶子节点分裂”->“上层节点更新”->“创建新根节点”**三部分。

叶子节点分裂：

  // 1. 分裂叶子节点（原节点和新节点分配键值对）int first_size = (leaf_page->GetMaxSize() + 2) / 2;int second_size = leaf_page->GetMaxSize() + 1 - first_size;page_id_t new_leaf_id = bpm_->NewPage();WritePageGuard new_leaf_guard = bpm_->WritePage(new_leaf_id);auto new_leaf_page = new_leaf_guard.AsMut<LeafPage>();ctx.write_set_.push_back(std::move(new_leaf_guard));new_leaf_page->Init(leaf_max_size_);// 随时记得更新各结点size_new_leaf_page->SetSize(second_size);leaf_page->SetSize(first_size);// 记得修改原叶子节点和新叶子结点的next_page_id_new_leaf_page->SetNextPageId(leaf_page->GetNextPageId());leaf_page->SetNextPageId(new_leaf_id);// 2. 根据插入位置分配键值对（原节点或新节点）if (insert_index < first_size) {// 插入位置在原节点：先移动原节点溢出的键到新节点，再插入新键for (int i = 0; i < second_size; i++) {new_leaf_page->SetKeyAt(i, leaf_page->KeyAt(i + first_size - 1));new_leaf_page->SetValueAt(i, leaf_page->ValueAt(i + first_size - 1));}for (int i = first_size - 1; i > insert_index; i--) {leaf_page->SetKeyAt(i, leaf_page->KeyAt(i - 1));leaf_page->SetValueAt(i, leaf_page->ValueAt(i - 1));}leaf_page->SetKeyAt(insert_index, key);leaf_page->SetValueAt(insert_index, value);} else {// 插入位置在新节点：先移动部分键到新节点，再插入新键for (int i = 0; i < insert_index - first_size; i++) {new_leaf_page->SetKeyAt(i, leaf_page->KeyAt(i + first_size));new_leaf_page->SetValueAt(i, leaf_page->ValueAt(i + first_size));}new_leaf_page->SetKeyAt(insert_index - first_size, key);new_leaf_page->SetValueAt(insert_index - first_size, value);for (int i = insert_index - first_size + 1; i < second_size; i++) {new_leaf_page->SetKeyAt(i, leaf_page->KeyAt(i + first_size - 1));new_leaf_page->SetValueAt(i, leaf_page->ValueAt(i + first_size - 1));}}

1. 计算分裂后两个节点的大小：

   int first_size = (leaf_page->GetMaxSize() + 2) / 2;
   int second_size = leaf_page->GetMaxSize() + 1 - first_size;
   

   first_size 是原节点保留的键数，值为 (maxsize + 1) / 2 的向上取整，这样是为了让分裂后的第一个节点数量要么等于第二个节点数量，要么比第二个节点数量大一。

2. 创建新叶子节点：
   分配新页面，初始化并设置大小为second_size，原节点大小改为first_size

3. 维护叶子节点链表：
   叶子节点通过next_page_id组成链表，方便范围查询。这里设置：

   • 原节点 leaf_page 的next指向新节点 new_leaf_id
   • 新节点 new_leaf_page的next继承原节点 leaf_page 的next

4. 根据插入位置分配键值对

   • 若新键属于原节点范围（insert_index < first_size）：先将原节点中 “溢出” 的键（超出first_size的部分）移到新节点，再在原节点中腾出位置插入新键。
   • 若新键属于新节点范围（insert_index ≥ first_size）：先将原节点中属于新节点的部分键移到新节点，插入新键后，再移动剩余键到新节点的对应位置。
     两种情况均保证分裂后两节点的键值对保持有序（从小到大）。

例如 4 阶 B+ 树：

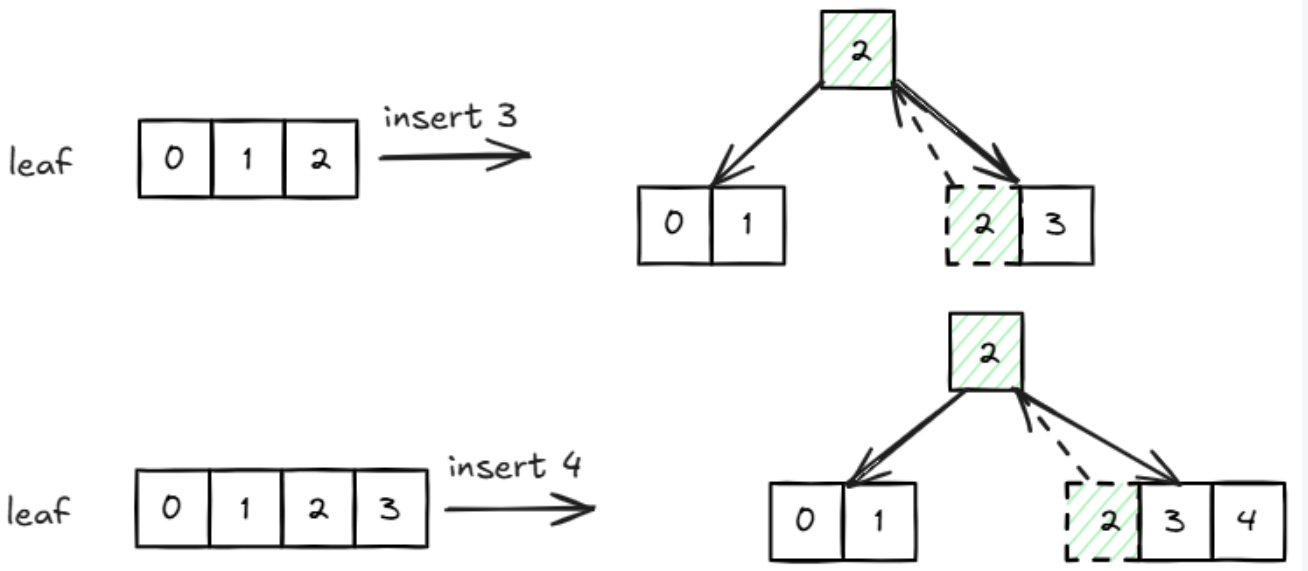
上层节点更新：

  // 1. 准备向上层节点插入的信息（新叶子节点的第一个键）KeyType insert_key = new_leaf_page->KeyAt(0);ctx.write_set_.pop_back();ctx.write_set_.pop_back();page_id_t first_split_page_id = ctx.root_page_id_;page_id_t second_split_page_id = new_leaf_id;bool new_root_flag = true;// 2. 逐层向上更新父节点（可能触发递归分裂）while (!ctx.write_set_.empty()) {int insert_index = ctx.indexes_.back() + 1;auto internal_page = ctx.write_set_.back().AsMut<InternalPage>();int size = internal_page->GetSize();if (size < internal_page->GetMaxSize()) {for (int i = size; i > insert_index; i--) {internal_page->SetKeyAt(i, internal_page->KeyAt(i - 1));internal_page->SetValueAt(i, internal_page->ValueAt(i - 1));break;}// 3.当内部结点已满时，继续进行分裂int first_size = (internal_page->GetMaxSize() + 2) / 2;int second_size = internal_page->GetMaxSize() + 1 - first_size;page_id_t new_internal_id = bpm_->NewPage();WritePageGuard new_internal_guard = bpm_->WritePage(new_internal_id);auto new_internal_page = new_internal_guard.AsMut<InternalPage>();ctx.write_set_.push_back(std::move(new_internal_guard));new_internal_page->Init(internal_max_size_);new_internal_page->SetSize(second_size);internal_page->SetSize(first_size);if (insert_index < first_size) {KeyType tmp_key = internal_page->KeyAt(first_size - 1);for (int i = 0; i < second_size; i++) {if (i > 0) {new_internal_page->SetKeyAt(i, internal_page->KeyAt(i + first_size - 1));}new_internal_page->SetValueAt(i, internal_page->ValueAt(i + first_size - 1));}for (int i = first_size - 1; i > insert_index; i--) {internal_page->SetKeyAt(i, internal_page->KeyAt(i - 1));internal_page->SetValueAt(i, internal_page->ValueAt(i - 1));}internal_page->SetKeyAt(insert_index, insert_key);internal_page->SetValueAt(insert_index, second_split_page_id);insert_key = tmp_key;} else {for (int i = 0; i < insert_index - first_size; i++) {if (i > 0) {new_internal_page->SetKeyAt(i, internal_page->KeyAt(i + first_size));}new_internal_page->SetValueAt(i, internal_page->ValueAt(i + first_size));}KeyType tmp_key;if (insert_index > first_size) {new_internal_page->SetKeyAt(insert_index - first_size, insert_key);tmp_key = internal_page->KeyAt(first_size);} else {tmp_key = insert_key;}new_internal_page->SetValueAt(insert_index - first_size, second_split_page_id);for (int i = insert_index - first_size + 1; i < second_size; i++) {new_internal_page->SetKeyAt(i, internal_page->KeyAt(i + first_size - 1));new_internal_page->SetValueAt(i, internal_page->ValueAt(i + first_size - 1));}insert_key = tmp_key;}second_split_page_id = new_internal_id;ctx.write_set_.pop_back();ctx.write_set_.pop_back();ctx.indexes_.pop_back();}  }internal_page->SetKeyAt(insert_index, insert_key);internal_page->SetValueAt(insert_index, second_split_page_id);internal_page->SetSize(size + 1);new_root_flag = false;ctx.write_set_.clear();ctx.indexes_.clear();

叶子节点分裂后，需将新节点的索引同步到上层内部节点，否则无法通过索引找到新节点，核心原理是：

1. 向上传递的索引键：新叶子节点的第一个键（new_leaf_page->KeyAt(0)）作为索引，需插入其父节点，标识新节点的键范围起点。
2. 父节点更新逻辑：
   • 若父节点未满：直接在父节点中插入索引键和新节点 ID，调整原有键和子节点的位置以保持有序，更新父节点大小后结束。
   • 若父节点已满：触发内部节点分裂，分裂规则与叶子节点类似（first_size向上取整），但存在关键差异：
     • 内部节点存储的是 “子节点索引键” 和 “子节点 ID”，其size表示子节点数量（比键数量多 1）。
     • 分裂时，中间位置的键不保留在分裂后的两节点中，而是作为新的索引键向上传递（用于更新更上层节点）。
3. 递归传导：上述分裂过程会逐层向上重复，直到某层节点未满可容纳新索引键，或到达原根节点。

创建新根节点：

  if (new_root_flag) {page_id_t new_root_id = bpm_->NewPage();WritePageGuard new_root_guard = bpm_->WritePage(new_root_id);auto new_root_page = new_root_guard.AsMut<InternalPage>();ctx.write_set_.push_back(std::move(new_root_guard));new_root_page->Init(internal_max_size_);// 这里size_应该设置为2，因为internal page 的size_指的是value的数量，是key的数量加一new_root_page->SetSize(2);new_root_page->SetKeyAt(1, insert_key);new_root_page->SetValueAt(0, first_split_page_id);new_root_page->SetValueAt(1, second_split_page_id);auto head_page = ctx.header_page_->AsMut<BPlusTreeHeaderPage>();head_page->root_page_id_ = new_root_id;ctx.write_set_.clear();}

若分裂过程传导至原根节点（原根节点也已满并分裂），则需创建新根节点，核心原理是：

• 新根节点为内部节点，存储原根节点和分裂出的新内部节点的 ID，并以 “向上传递的索引键” 作为两者的分界键。
• 更新头页面（BPlusTreeHeaderPage）中的根节点 ID 为新根的 ID，树的高度增加 1。

可以参考B+ Tree Visualization提供的可视化动画理解整个过程。

B+ Tree 删除

删除总共有两大部分，合并相邻节点和重新分配。

当合并 leaf page 后，删除父节点中对应的 key 比较简单，直接删除即可。例如 4 阶 B+ 树：

首先需要定位到存储目标键的叶子节点，删除该节点中对应的键值对后，检查节点大小是否是否小于最小容量。若小于min size，首先尝试从两侧的兄弟节点（即与当前节点拥有相同父节点的节点）中 “借用” 一个键值对。若存在某一侧的兄弟节点有富余的键值对（容量大于min size），则成功完成借用后即可结束操作；若两侧兄弟节点均无富余键值对，则需选择一侧兄弟节点进行合并。

借用过程较为直接：从左侧兄弟节点借用时，将左侧节点的最后一个键值对转移至当前节点的最前端；从右侧兄弟节点借用时，将右侧节点的第一个键值对转移至当前节点的末尾。叶子节点与内部节点的借用流程基本一致，仅需注意内部节点借用后需同步更新子节点的父节点指针。

相对复杂的是合并过程。同样需选择左侧或右侧的兄弟节点进行合并，将其中一个节点的所有键值对转移至另一个节点中。若合并的是叶子节点，需记得更新节点的 next page id 以维护链表连续性；若合并的是内部节点，则需更新合并后节点的所有子节点的父节点指针。完成节点合并后，然后，删除 parent 节点中对应的 key。删除后，再次检查 size 是否小于 min size，形成向上递归。

在合并叶子节点后，从父节点中删除对应索引键的操作较为简单，直接移除即可。例如在 4 阶 B + 树中：

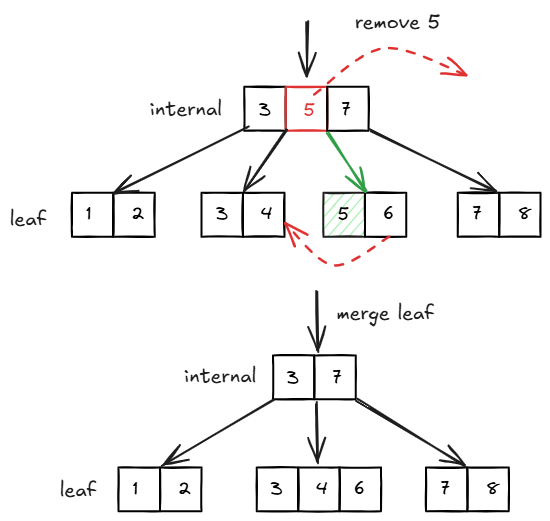
合并 internal page 后，并不是简单地删除父节点中对应 key，而是有一个父节点 key 下推的过程：

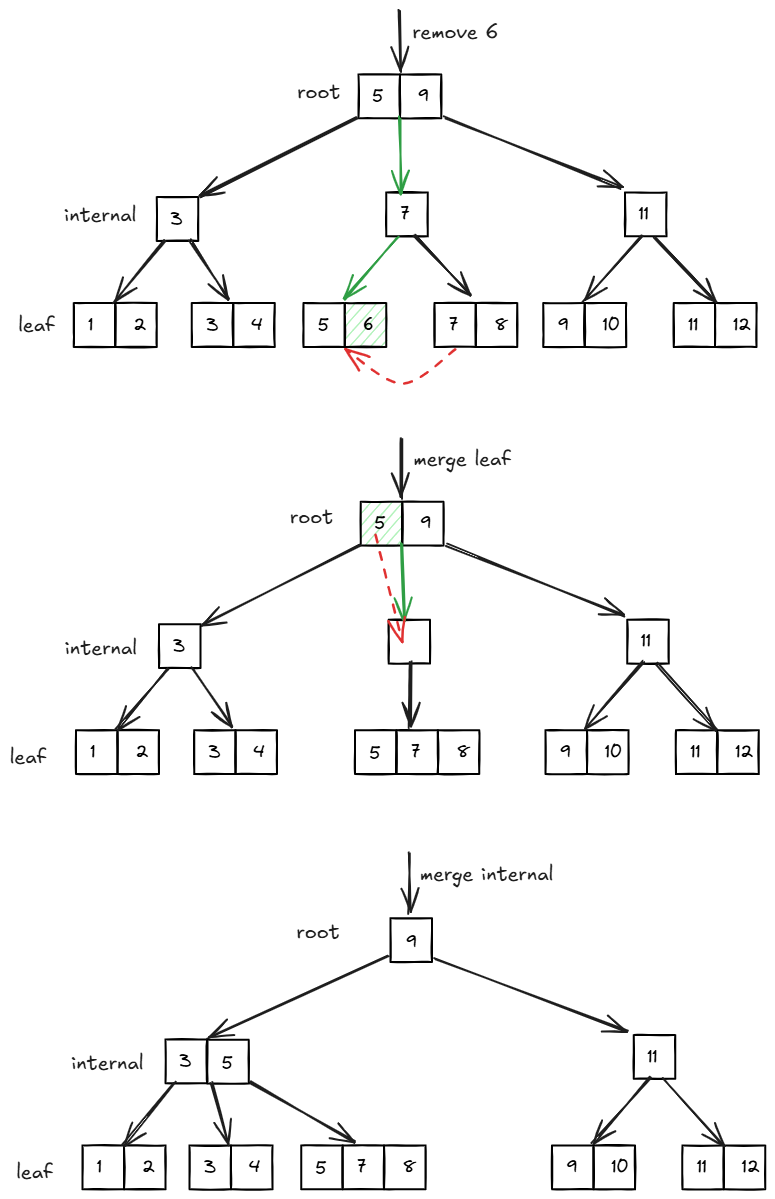
需要注意的是，root page 并不受 min size 的限制。但如果 root page 被删到 size 只剩 1，即只有一个 child page 的时候，应将此 child page 设置为新的 root page。

root page 的 min size 与节点类型相关。如果 root page 是 internal page，则 min size == 2，如果是 leaf page，则 min size == 1。这是因为 root page 若子节点数量太少（≤1），会失去索引意义（若根节点只有 1 个键、2 个子节点，查询时总是直接定位到其中一个子节点，根节点本身没有起到分流作用）。

另外，在合并时，两个 page 合并成一个 page，另一个 page 应该删除，释放资源。删除 page 时，仍是调用 buffer pool 的 DeletePage() 函数。

和 Insert 类似，Delete 过程也是先向下递归查询 leaf page，不满足 min size 后先尝试偷取，无法偷取则合并，并向上递归地检查是否满足 min size。

---

代码流程和插入的相似，均通过乐观锁和悲观锁策略进行优化。

乐观锁情况下，无需借键或合并，只需先按读锁找到叶子节点，然后将该叶子节点升级为写锁，最后执行删除（叶子节点当前大小 > 最小容量（GetMinSize()））。

如果乐观锁没能删除成功，则进入悲观锁策略。

悲观锁需全程持有读锁导航到目标叶子节点，同时记录路径中的父节点索引（ctx.indexes_），确保操作过程中持有所有相关节点的锁（防止死锁），然后在悲观锁保护下，从叶子节点中物理删除指定键。

若删除后节点大小 < 最小容量，需要通过 “借键” 或 “合并” 恢复平衡，并将影响逐层向上传导。流程为：

1. 若当前节点是根节点：

   • 若为叶子节点且大小为 0，更新头页面的根节点 ID 为INVALID_PAGE_ID。
   • 若为内部节点且大小 ≤ 1，删除原根节点，更新根节点为合并后的节点 ID。

2. 若当前节点大小 ≥ 最小容量，直接返回。

3. 左借键：若存在左兄弟（index > 0）且左兄弟大小 > 最小容量（有多余键可借），调用BorrowFromLeft：左兄弟将最大键移到当前节点，同时更新父节点的索引键，借键后节点大小恢复，返回。

4. 尝试右借键：若左借失败，检查右兄弟（index < 父节点大小-1）且右兄弟大小 > 最小容量，调用BorrowFromRight：右兄弟将最小键移到当前节点，更新父节点索引键，返回。

5. 若借键失败（兄弟节点均无多余键），则与兄弟节点合并：

   • 左合并（有左兄弟时）：当前节点与左兄弟合并，左兄弟吸收当前节点的所有键，父节点删除对应子节点索引。

   • 右合并（无左兄弟时）：当前节点吸收右兄弟的所有键，父节点删除右兄弟的索引。

   • 合并后，删除被合并的节点（释放页面），并向上层节点（父节点）继续循环处理（因为父节点可能因删除子节点而大小低于最小值）。

遇到的问题

1.释放叶子结点的读锁后，在获取写锁之前存在时间空窗，在此时间可能被其他线程获得写锁，修改了叶子结点之后，本线程才获得写锁，此时叶子结点已经被修改。之后的操作也会存在数据一致性问题

ctx.read_set_.clear();
ctx.write_set_.push_back(bpm_->WritePage(page_id));
op_write_page = ctx.write_set_.back().AsMut<BPlusTreePage>();

因此应该修改为直接获取写锁，不应该设置读写锁升级过程，避免时间空窗

op_write_page = ctx.write_set_.back().AsMut<BPlusTreePage>(); 

2.合并叶子节点后未同步next_page_id，导致叶子节点链表断裂，影响范围查询。

// MergeWithLeft中修复：更新左叶子节点的next指针
left_leaf_page->SetNextPageId(leaf_page->GetNextPageId());// MergeWithRight中修复：更新当前叶子节点的next指针
leaf_page->SetNextPageId(right_leaf_page->GetNextPageId());

Task #3 - Index Iterator

Task3 的目的是实现B+树的迭代器，以便支持对叶子页中数据的中序扫描。

需要修改的文件：

• src/include/storage/index/index_iterator.h
• src/index/storage/index_iterator.cpp

在此之前，Task#2 中的 B+树部分还有 begin () 和 end () 方法暂未实现，因为我觉得这部分其实也算迭代器的一部分，所以我挪到 Task#3 一起实现，测试留到最后一起做。

B+树迭代器

这部分只需要实现 begin() 、Begin(const KeyType &key)和 end() ，begin() 包括两个重载。

begin() 返回 B+ 树中最小元素（最左侧叶子节点的第一个元素）的迭代器，实现比较简单。首先，从根节点开始，一直向左遍历到最左侧的叶子节点；然后，在叶子节点中，从索引 0 开始迭代；如果树为空（根节点无效），直接返回结束迭代器。

但注意，返回值的类型为 INDEXITERATOR_TYPE，它是 IndexIterator 模板类的宏定义，返回迭代器时如果传入了一些参数，比如 bpm、page_id和index，我们需要为 IndexIterator 定义一个对应的构造函数，比如：

IndexIterator(BufferPoolManager *bpm, page_id_t page_id, int index);

Begin (const KeyType &key) 返回第一个大于等于指定 key 的元素的迭代器，思路是从根节点出发，逐层向下遍历到叶子节点，最终在叶子节点中定位到目标位置。

流程其实和 begin() 差不多，只不过begin() 始终是左遍历，前者需要通过 KeyBinarySearch(page, key) 对比导航到目标叶子节点，然后在叶子节点内调用 KeyBinarySearch(page, key) 定位目标的所以，最后返回 INDEXITERATOR_TYPE(bpm_, page_guard.GetPageId(), index)

end() 是超尾，直接返回 INDEXITERATOR_TYPE(bpm_, INVALID_PAGE_ID, -1) 就行。

Index Iterator

IndexIterator 类需要我们自定义构造函数和成员变量以实现以下方法：

• isEnd ()：返回当前迭代器是否指向最后一个键值对。
• operator++()：移动到下一个键值对。
• operator*()：返回当前迭代器指向的键值对。
• operator==()：返回两个迭代器是否相等。
• operator!=()：返回两个迭代器是否不相等。

默认构造函数为：

IndexIterator(BufferPoolManager *bpm, page_id_t page_id, int index);

注意，在迭代器形成后，需临时持有该页的读锁，然后再将键值对存储至 result_。

私有成员变量有：

BufferPoolManager *bpm_; 
page_id_t page_id_;      
int index_;              
std::pair<KeyType, ValueType> result_; 

page_id_ 是存有目标的叶子页id，index_是当前叶子页中目标键值对的索引（之前用ReadPageGuard作为成员导致死锁，因此改为存储page_id_而非直接持有页锁，避免长期持有锁导致其他操作无法访问该页）；result_ 缓存目标键值对，避免每次调用operator*()时都重新读取页。

---

迭代器方法的实现都比较简单，大部分只需返回成员变量即可。

isEnd() 返回 index_ == INVALID_PAGE_ID 判断是否为最后一个键值对；

operator*() 返回 result_ 即可；

operator++() 实现稍微复杂一点，需要从当前位置移动到下一个键值对，若当前页已遍历完，则通过叶子节点的链表（GetNextPageId()）切换到下一个叶子页

operator== 和 operator!= 只需要判断两个迭代器的 page_id_ 和 index_ 变量是否相同即可。

test

test/storage/b_plus_tree_concurrent_test.cpptest/storage/b_plus_tree_contention_test.cpptest/storage/b_plus_tree_delete_test.cpptest/storage/b_plus_tree_insert_test.cpptest/storage/b_plus_tree_sequential_scale_test.cpp

首先cd到build目录下，然后将上述文件中所有测试函数第二个形参的前缀DISABLE_去掉，执行命令：

make b_plus_tree_concurrent_test -j `nproc`
./test/b_plus_tree_concurrent_testmake b_plus_tree_contention_test -j `nproc`
./test/b_plus_tree_contention_testmake b_plus_tree_delete_test -j `nproc`
./test/b_plus_tree_delete_testmake b_plus_tree_insert_test -j `nproc`
./test/b_plus_tree_insert_testmake b_plus_tree_sequential_scale_test -j `nproc`
./test/b_plus_tree_sequential_scale_test

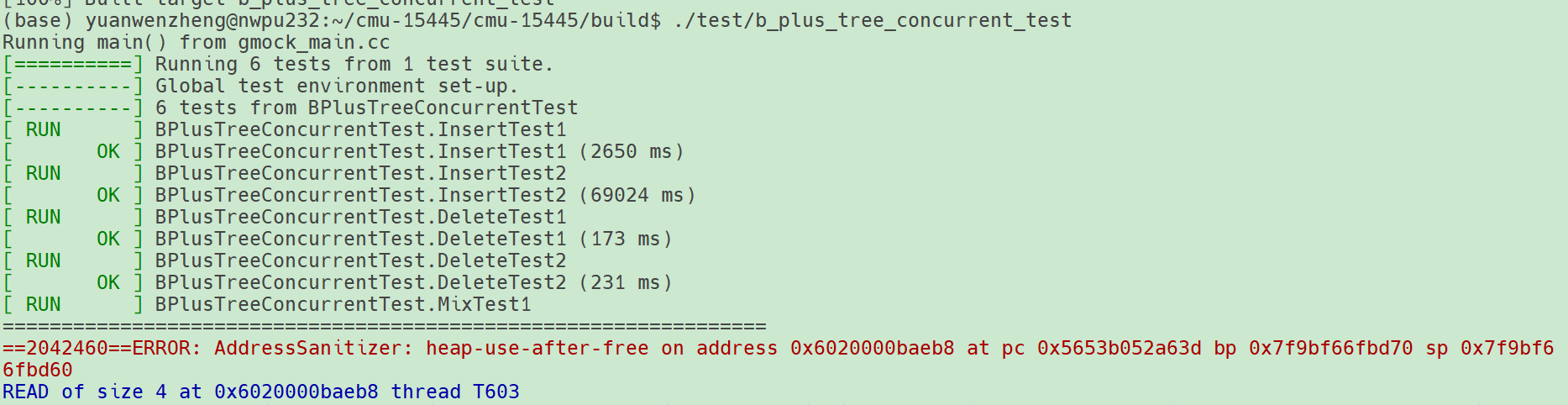
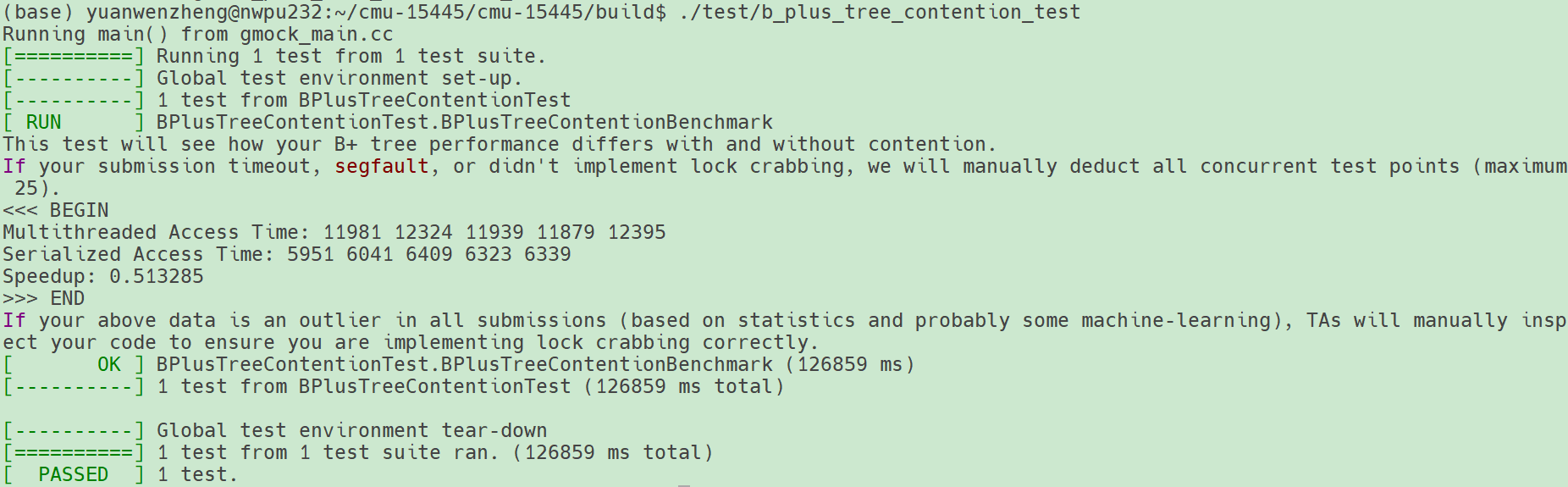
测试在 b_plus_tree_concurrent_test 的 BPlusTreeConcurrentTest.MixTest1中发生了 heap-use-after-free ，debug调试看看。

调用栈定位到问题发生在lab1 中的 BufferPoolManager 对page_table_的操作中，问题如下：

1. 线程 T603 在BufferPoolManager::CheckedWritePage中，通过std::unordered_map::operator[]分配了一个键值对
2. 线程 T602 在BufferPoolManager::CheckedReadPage中，通过std::unordered_map::erase释放了同一个键值对
3. 线程 T603 在BufferPoolManager::DeletePage中，再次通过std::unordered_map::erase尝试删除同一个条目，但此时该条目已被 T602 释放，导致访问了已释放的内存，触发 heap-use-after-free。

根本原因是锁没设置好，在 1 和 2 中间存在时间空窗，导致 it 在这个空窗内被删除了，因此 2 重新持有锁时，会发生 heap-use-after-free。解决方法很简单，在 2 发生重新持有锁后，再次获取 it 然后判断是否有效。

// 问题
lk.unlock();  // 1
// 写回脏页
if (frame->is_dirty_) {
FlushPage(page_id);
}
lk.lock();  // 2
page_table_.erase(it);    // 解决
lk.unlock();
// 写回脏页
if (frame->is_dirty_) {
FlushPage(page_id);
}
lk.lock();
// 重新查找
it = page_table_.find(page_id);
if (it == page_table_.end() || it->second != frame_id) {
return true;
}
if (frame->pin_count_ > 0) {
return false;
}
page_table_.erase(it);

重新测试

测试成功。

这个错误让我没想到，因为 lab1 通过了本地的所有测试并提交 Gradescope 成功，但还是出现了一些未检测出来的问题。

submit

先在build文件夹下依次执行以下命令：

make format
make check-clang-tidy-p1

然后执行：

make submit-p2

会在根目录下生成名为 project2-submission.zip的压缩包，将其上传至 Gradescope即可

我提交检测的时候，说除了所需的代码文件外，还需要 GRADESCOPE.md 签名文件，大概查了下，这是23年开始新加的要求，除了PROJECT#0不需要外，其他项目都需要。运行下面指令生成：

cd ..
python3 gradescope_sign.py

然后填一下自己的名字、院校和Github ID即可，GRADESCOPE.md 会自行添加至刚才生成的project2-submission.zip压缩包中。

满分通过。

排名中上

其实从 lab2 开始，完成的人正在逐渐减少，希望能坚持到最后。