MLS学习
1.前言
问ai等,查看资料并记录
2.记录
deepseek.ai






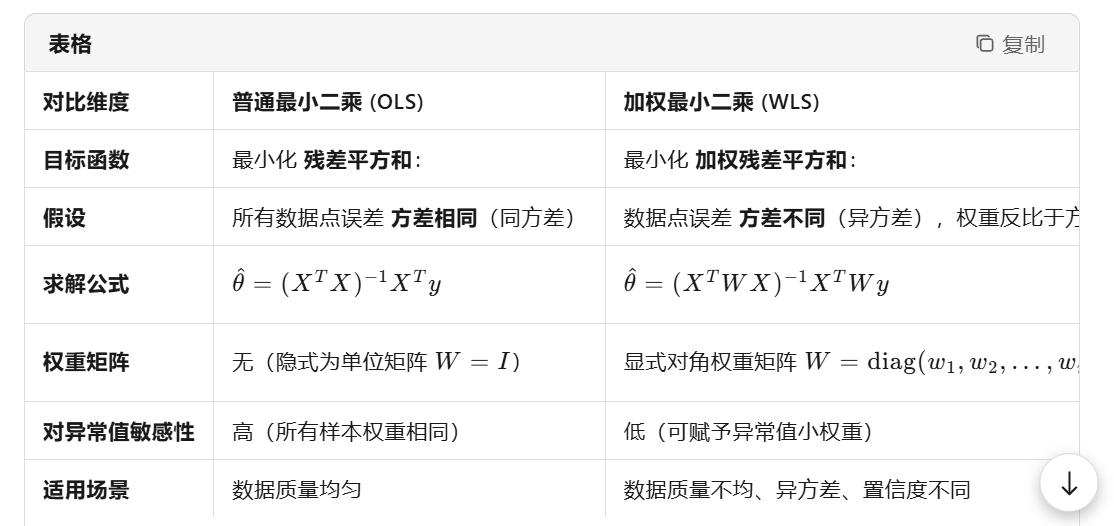
关键区别
| 特征 | fit_params_1 | fit_params_2 |
|---|---|---|
| 坐标系统 | 相对中心点偏移 (Δx,Δy)(Δx,Δy) | 绝对坐标 (x,y)(x,y) |
| 权重应用方式 | 最小化 ∑wi⋅残差2∑wi⋅残差2 | 最小化 ∑wi2⋅残差2∑wi2⋅残差2 |
| 设计矩阵构造 | 先构造 AA,后与 WW 相乘 | 直接构造 Aweighted=WA0Aweighted=WA0 |
| 数学等价性 | 标准加权最小二乘 (WLS) | 权重被平方的加权最小二乘 |
| 求解效率 | 需计算 ATWAATWA(显式正规方程) | 直接求解 Aθ=bAθ=b(隐式) |
kimi.ai
fit_params_1 = np.linalg.lstsq(AWA, AWb, rcond=None)[0]
AWA 是一个6x6的矩阵,AWb是一个6x1的矩阵
fit_params_2 = np.linalg.lstsq(A, b, rcond=None)[0]
A是一个 nx6的矩阵, b是一个长度为n的一维向量注意:
fit_params_1中:basis_funcs = [lambda x, y: x ** 2,lambda x, y: y ** 2,lambda x, y: x * y,lambda x, y: x,lambda x, y: y,lambda x, y: 1,]A = np.zeros((len(local_points), len(basis_funcs))) #矩阵大小 mx6
b = local_points[:, 2]for i, func in enumerate(basis_funcs):A[:, i] = [func(pt[0] - x, pt[1] - y) for pt in local_points]
W = np.diag(weights) ## 将权重向量转换为对角矩阵
AWA = A.T @ W @ A
AWb = A.T @ W @ b fit_params_2中:
A = np.vstack([x_neigh ** 2 * weights, y_neigh ** 2 * weights, x_neigh * y_neigh * weights, x_neigh * weights,y_neigh * weights, weights]).T
b = z_neigh * weights 请分别给出fit_params_1 与 fit_params_2 的详细计算方法过程表格
| 计算步骤 | fit_params_1 | fit_params_2 |
|---|---|---|
| 加权方式 | A 和 b 未加权,权重通过 AWA = AᵀWA 和 AWb = AᵀWb 引入 | A 和 b 直接加权,即 A = [x²*w, y²*w, ..., 1*w] |
| 矩阵维度 | AWA 是 6×6,AWb 是 6×1 | A 是 m×6,b 是 m×1 |
| 最小二乘形式 | 正规方程法:(AᵀWA)θ = AᵀWb | 直接最小二乘:Aθ ≈ b |
但 数值上,如果 weights 相同,fit_params_1 和 fit_params_2 的结果应该完全一致,因为:
fit_params_1 是 加权最小二乘的正规方程解。
fit_params_2 是 加权最小二乘的直接解,等价于
fit_params_1。
因此,两者本质相同,只是计算方式不同
问题:
加权最小二乘的正规方程解 具体计算过程:
fit_params_1
表格
| 步骤 | 计算内容 |
|---|---|
| 1 | 构造 X(m×6)和 y(m×1) |
| 2 | 构造对角权重矩阵 W(m×m) |
| 3 | 计算 XTWX(6×6) |
| 4 | 计算 XTWy(6×1) |
| 5 | 解正规方程 θ=(XTWX)−1XTWy |
问题 加权最小二乘的直接解 具体计算过程:
fit_params_2
表格
| 步骤 | 计算内容 |
|---|---|
| 1 | 构造原始设计矩阵 X(m×6)和观测向量 y(m×1) |
| 2 | 计算权重矩阵的平方根 W1/2=diag(wi) |
| 3 | 构造加权数据 X~=W1/2X、y~=W1/2y |
| 4 | 解普通最小二乘 θ=np.linalg.lstsq(X~,y~) |
