07-一般的树

1. 树的概念

树: 逻辑结构是一对多的, 类似于"树状"的数据结构形式.

• 结点的度：树中一个结点孩子的个数称为该结点的度。
• 树的度：树中结点最大的度数称为树的度。
• 树的高度 (深度）：树中结点的最大层数称为树的高度 (深度)
• 路径：树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的，路径长度为序列中边的个数。

• 孩子顺序性分类

• • 有序树：结点的子树按照从左往右的顺序排列，不能更改。
  • 无序树：结点的子树之间没有顺序，随意更改。

注: 这个认知会在我们后续学习二叉树的时候用到，因为二叉树需要区分左右孩子

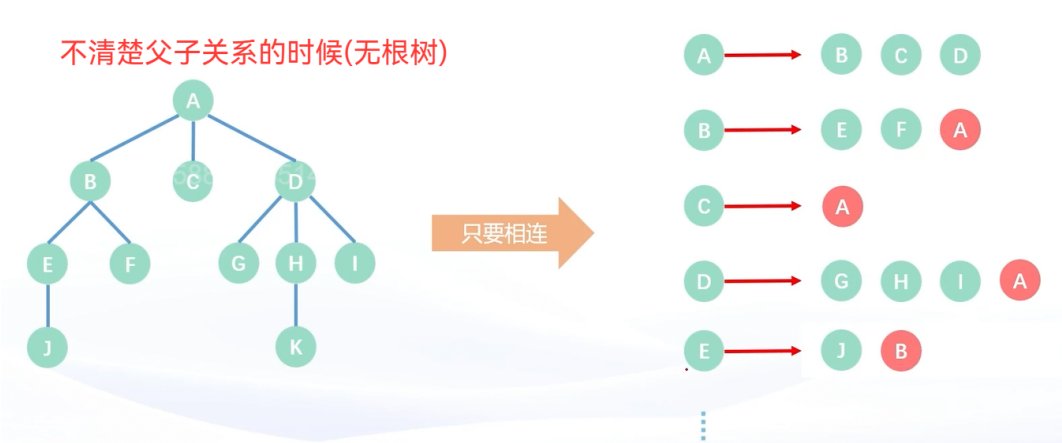
• 有根树和⽆根树

• • 有根树：树的根节点已知，是固定的
  • 无根树：树的根节点未知，谁都可以是根结点

注: 这个认知主要会影响我们对于树的存储。

如果是无根树，父子关系不明确，此时我们需要把所有的情况都存下来。比如a和b之间有一条边，我们不仅要存a有一个孩子b，也要存b有一个孩子a。

甚至有的时候，在有根树的题目里，也要这样存储。

2. 树的存储 -> 孩子表示法

孩子表示法: 将每个节点的孩子信息存储下的一种树的存储方法.

• vector数组实现
• 链式前向星实现

2.1. vector数组实现

#include <iostream>
#include <vector>using namespace std;const int N = 1e5 + 10;int n;
vector<int> edges[N]; // 存储树int main()
{cin >> n;for(int i = 1; i < n; i++){int a, b; cin >> a >> b;// a 和 b 之间有一条边edges[a].push_back(b);edges[b].push_back(a);}return 0;
}

2.2. 链式前向星实现

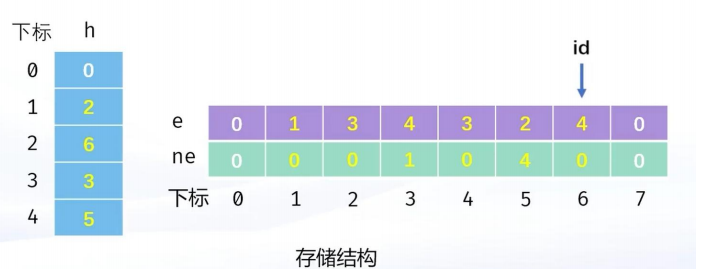
#include <iostream>using namespace std;const int N = 1e5 + 10;// 链式前向星
int h[N], e[N * 2], ne[N * 2], id; // 无根树需要存储两遍根
int n;// 其实就是把 b 头插到 a 所在的链表后面
void add(int a, int b)
{id++;e[id] = b;ne[id] = h[a];h[a] = id;
}int main()
{cin >> n;for(int i = 1; i < n; i++){int a, b; cin >> a >> b;// a 和 b 之间有一条边add(a, b); add(b, a);}return 0;
}

3. 树的遍历

3.1. DFS

DFS: 优先遍历完一条路径, 再考虑其他路径的遍历方式.

// vector<type>[N]存储
void dfs(int u)
{cout << u << " ";st[u] = true; // 当前这个点已经访问过了// 访问所有的孩子for(auto v : edges[u]){if(!st[v]){dfs(v);}}
}// 用链式前向星存储
// 存图
int h[N], e[N * 2], ne[N * 2], id; // 无根树, 存储边要存储两遍
int n;bool st[N]; // 标记哪些点已经访问过了void add(int a, int b)
{id++;e[id] = b;ne[id] = h[a];h[a] = id;
}void dfs(int u)
{cout << u << " ";st[u] = true;for(int i = h[u]; i; i = ne[i]){int v = e[i]; // 孩子if(!st[v]){dfs(v);}}
}
// 注: 链表存储方式遍历会反着, 因为用的是头插

3.2. BFS

BFS: 层层访问, 同一层访问完了再访问下一层.

void bfs()
{queue<int> q;q.push(1);st[1] = true;while(q.size()){int u = q.front(); q.pop();cout << u << " ";for(auto v : edges[u]){if(!st[v]){q.push(v);st[v] = true;}}}
}void bfs()
{queue<int> q;q.push(1);st[1] = true;while(q.size()){int u = q.front(); q.pop();cout << u << " ";for(int i = h[u]; i; i = ne[i]){int v = e[i];if(!st[v]){q.push(v);st[v] = true;}}}
}
// 注: 链表存储方式遍历会反着, 因为用的是头插