当前位置：首页 > news >正文

机器学习通关秘籍｜Day 03：决策树、随机森林与线性回归

news 2025/8/6 7:54:02

一、决策树

1、概念

2、基于信息增益的决策树的建立

（1）信息熵

（2）信息增益

（3）信息增益决策树建立步骤

3、基于基尼指数的决策树的建立

4、API

二、随机森林

1、算法原理

2、API

三、线性回归

1、回归

2、线性回归

3、损失函数

4、多参数回归

5、最小二乘法

6、API

四、总结

一、决策树

1、概念

决策树是一种常用的机器学习算法，用于解决 分类和回归问题。它通过递归地将数据集划分为子集，构建一棵树形结构，每个节点代表一个特征或属性的判断条件，叶子节点表示最终的分类结果。

2、基于信息增益的决策树的建立

决策树的核心思想是通过选择最优的特征进行划分，从而减少数据的不确定性。以下是基于信息增益的决策树建立步骤：

（1）信息熵

信息熵描述的是 不确定性。信息熵越大，不确定性越大。信息熵的值越小，则X的纯度越高。

信息熵是衡量数据集纯度的一个指标，公式如下：

示例：假设一个数据集中有 10 个样本，其中 6 个属于类别 A，4 个属于类别 B，则信息熵为：

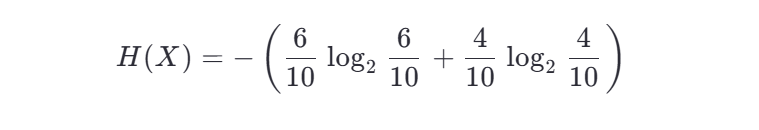
（2）信息增益

信息增益（Information Gain）是决策树中用于选择最优分裂特征的核心指标。它的基本思想是：选择能够最大程度降低数据不确定性的特征进行划分。不确定性由信息熵衡量，信息增益越大，说明使用该特征划分后，数据变得更“纯净”，分类效果更好。

信息增益是一个统计量，用来描述一个属性区分数据样本的能力。信息增益越大，那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量, 信息增益公式：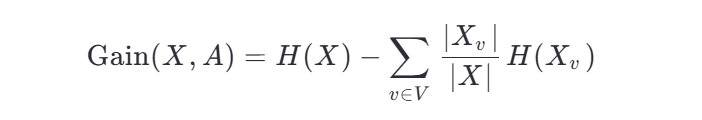

（3）信息增益决策树建立步骤

下面我们通过一个具体例子来详细计算信息增益：

假设我们有一个数据集共 10 个样本，目标是预测用户是否会购买某产品（类别 A：购买，类别 B：不购买）。我们考虑使用“天气”这一特征进行划分，其分布如下：

天气	样本数	购买	不购买
晴天	6	5	1
雨天	4	1	3
总计	10	6	4

我们的目标是计算使用“天气”作为分裂特征时的信息增益。

第一步：计算原始数据集的信息熵 H(X)

原始数据集中：

信息熵为：

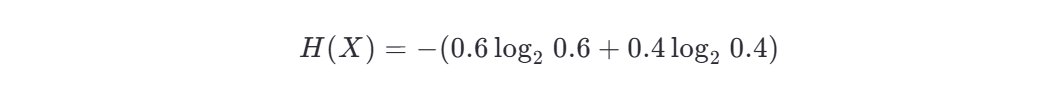
计算对数值（可使用计算器）：

代入：

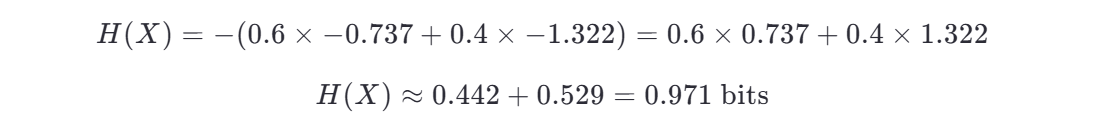
第二步：计算每个子集的信息熵 H(Xv)

(a) 晴天子集（6 个样本）

(b) 雨天子集（4 个样本）

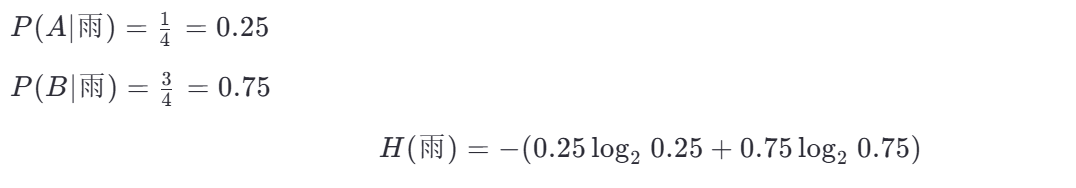
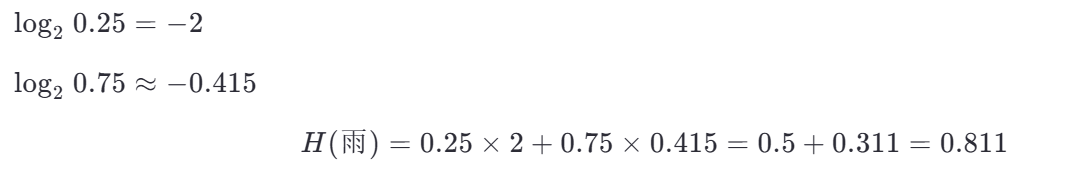
第三步：计算加权平均熵

第四步：计算信息增益

信息增益与决策判断的关系

信息增益越大，说明该特征对分类的帮助越大。在这个例子中，“天气”带来了 0.256 的信息增益，意味着通过“天气”划分后，整体数据的不确定性显著下降。
在构建决策树时，我们会比较所有特征的信息增益，选择增益最大的特征作为当前节点的分裂依据。
例如，如果另一个特征“温度”的信息增益是 0.32，大于“天气”的 0.256，那么我们就会优先选择“温度”进行分裂。
这体现了决策树的贪心策略：每一步都选择当前最优的特征，逐步构建一棵高效的分类树。

3、基于基尼指数的决策树的建立

基尼指数是另一种衡量数据集纯度的指标，公式如下：

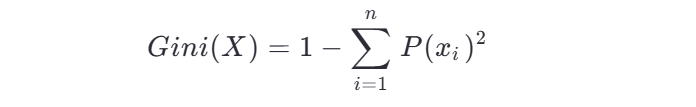
基尼指数越小，数据集的纯度越高。

4、API

代码示例：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.model_selection import train_test_split
x, y = load_iris(return_X_y=True)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
# 创建决策树模型
model = DecisionTreeClassifier()
model.fit(x_train, y_train)
print(model.score(x_test, y_test))y_pred = model.predict([[4.3, 2.6, 1.5, 1.3]])
print(y_pred)
# 导出已经构建的据册数
export_graphviz(model, out_file='../src/tree.txt', feature_names=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'])

结果展示：

二、随机森林

森林，顾名思义，就是有很多棵树。

1、算法原理

随机森林是一种基于决策树的集成学习方法，通过构建多棵决策树并结合它们的预测结果来提高模型的泛化能力。其核心思想包括：

Bootstrap 抽样：从原始数据集中有放回地抽取多个子集，每棵树使用不同的子集进行训练。
随机特征选择：在每个节点分裂时，只考虑一部分随机选择的特征，而不是全部特征。
投票机制：对于分类任务，最终预测结果是所有树的多数投票结果；对于回归任务，最终预测结果是所有树的平均值。

2、API

RandomForestClassifier ( n_estimators=100, max_depth=5, criterion='entropy' )

n_estimators: 树的数量,

max_depth: 树的最大深度,

criterion: 评价标准(entropy: 熵, gini: 基尼系数)

代码示例：

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 加载数据集
x, y = load_iris(return_X_y=True)
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
# 标准化
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
# 创建随机森林模型 n_estimators: 树的数量, max_depth: 树的最大深度, criterion: 评价标准(entropy: 熵, gini: 基尼系数)
model = RandomForestClassifier(n_estimators=100, max_depth=5, criterion='entropy')
model.fit(x_train, y_train)
score = model.score(x_test, y_test)
print(score)
# 预测新数据
y = model.predict([[1.3,2.5,1.1,0.5]])
print(y)

结果展示：

三、线性回归

1、回归

回归的目的是预测数值型的目标值y。最直接的办法是依据输入x写出一个目标值y的计算公式。假如你想预测某人的体重（因变量），根据他的身高（自变量）。通过收集一些人的身高和体重数据，我们可以找到它们之间的关系。

张三的体重 = 0.86 * 张三的身高 - 0.5 * 张三的运动时间

这就是所谓的回归方程（regression equation），其中的 0.86 和 0.5 称为回归系数（regression weights），求这些回归系数的过程就是回归。一旦有了这些回归系数，再给定输入，做预测就非常容易了。具体的做法是用回归系数乘以输入值，再将结果全部加在一起，就得到了预测值。

2、线性回归

概念：线性回归是回归的一种，它假设因变量与自变量之间存在线性关系。也就是说，可以用一条直线来近似描述它们的关系。
例子：如果身高和体重的关系是线性的，那么我们可以画一条直线，这条直线可以表示为：

其中，“斜率”表示身高每增加1单位，体重平均增加多少；“截距”表示当身高为0时的体重值（虽然实际中身高不可能为0，但这是数学上的起点）。

3、损失函数

（1）线性方程

我们为了让我们得到的 方程（模型）更加地贴近真实值，尽可能地提高准确率，由此提出了损失函数。

我们假设这个最优的方程是:

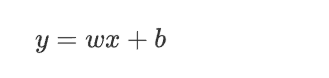
这样的直线随着w和b的取值不同可以画出无数条

（2）为了求解最优值，我们引入损失函数

在这无数条中,哪一条是比较好的呢?

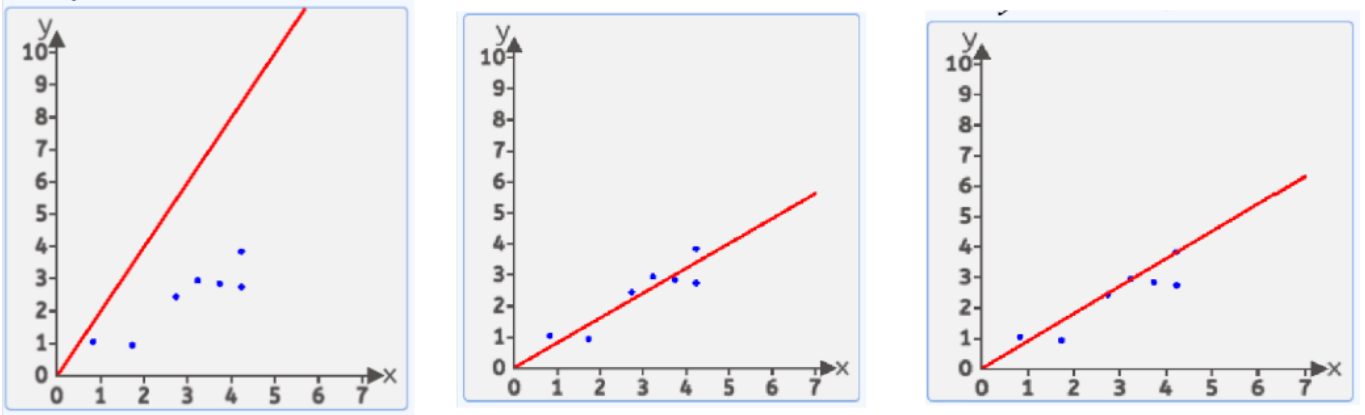
我们有很多方式认为某条直线是最优的,其中一种方式:均方差

就是每个点到线的竖直方向的距离平方求和在平均最小时这条直接就是最优直线

可能很多读者会疑惑一个问题：为什么我们要取竖直方向上的差值？而不是对于这一点向直线做垂线求距离呢？

我们只需要搞清楚，直线上的点代表着 预测值 ，而样本点的 y 值代表了真实值，所以竖直距离上的差值，就是误差

然后计算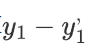表示第一个点的真实值和计算值的差值 ,然后把第二个点,第三个点...最后一个点的差值全部算出来

有的点在上面有点在下面,如果直接相加有负数和正数会抵消,体现不出来总误差,平方后就不会有这个问题了

所以最后:

总误差(也就是传说中的损失 ):

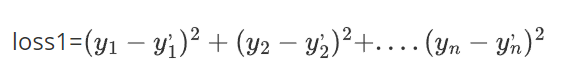
平均误差(总误差会受到样本点的个数的影响，样本点越多，该值就越大，所以我们可以对其平均化，求得平均值，这样就能解决样本点个数不同带来的影响)

这样就得到了传说中的损失函数:

（此处的 x值任取，只是举个例子）

怎么样让这个损失函数的值最小呢?

（3）利用初中抛物线的知识或者高中的求导知识求得最低点

我们先假设b=0

然后就简单了，算 w 在什么情况下损失函数的值最小( 初中的抛物线求顶点 的横坐标, 高中求导数为0时)

求得w=0.795时损失函数取得最小值

那我们最终那个真理函数(最优解)就得到了

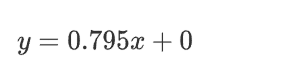
注意：

实际数据中 x 和 y 组成的点不一定是全部落在一条直线上
我们假设有这么一条直线 y=wx+b 是最符合描述这些点的
最符合的条件就是这个方程带入所有x计算出的所有y与真实的y值做 均方差计算
找到均方差最小的那个w
这样就求出了最优解的函数(前提条件是假设b=0)

4、多参数回归

概念：多参数回归是指自变量不止一个的情况。例如，除了身高外，还可能考虑年龄、性别等因素来预测体重。
例子：如果我们不仅用身高预测体重，还加入年龄作为另一个自变量，那么线性回归的公式就变成了：

这里有两个斜率，分别表示身高和年龄对体重的影响。

5、最小二乘法

概念：最小二乘法是一种优化方法，用于求解线性回归中的参数（如斜率和截距），使得损失函数（通常是均方误差）最小化。
目标：找到一组参数，使得损失函数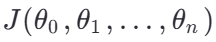最小。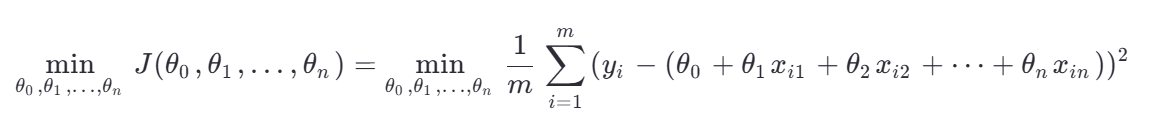
求解方法：可以通过解析法（如正规方程）或数值优化方法（如梯度下降）来求解最小化问题。
- 正规方程（适用于小规模数据）：
  
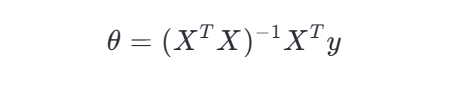
  其中：
- 梯度下降（适用于大规模数据）：
  
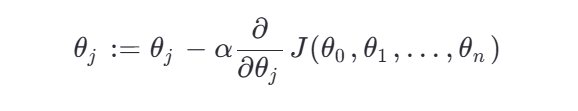
  其中：
例子：假设我们有几组身高和体重的数据，最小二乘法会调整直线的位置（即调整斜率和截距），使得所有数据点到直线的距离平方和最小。这样得到的直线就是最佳拟合直线。

6、API

代码示例：

from sklearn.linear_model import LinearRegression
import numpy as np
# 创建具有8个特征和1个目标值的数据集
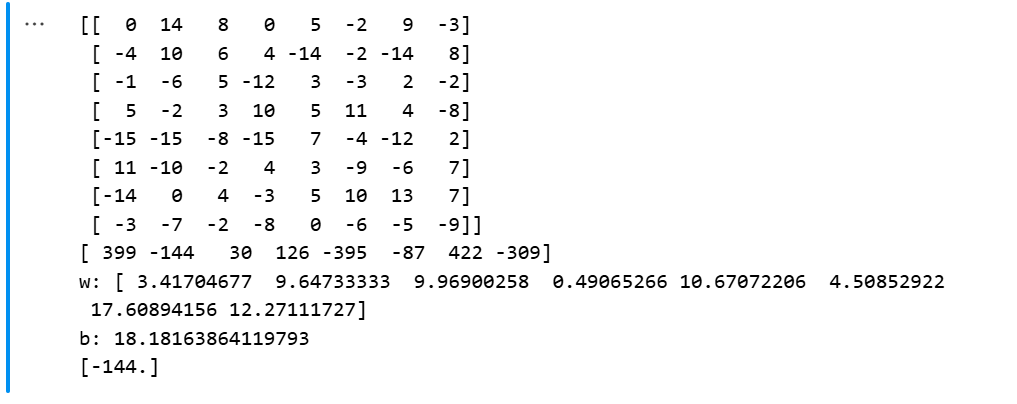
data=np.array([[0,14,8,0,5,-2,9,-3,399],[-4,10,6,4,-14,-2,-14,8,-144],[-1,-6,5,-12,3,-3,2,-2,30],[5,-2,3,10,5,11,4,-8,126],[-15,-15,-8,-15,7,-4,-12,2,-395],[11,-10,-2,4,3,-9,-6,7,-87],[-14,0,4,-3,5,10,13,7,422],[-3,-7,-2,-8,0,-6,-5,-9,-309]])
# 取全部行，除了最后一列的全部列，也就是八个特征
x = data[:, :-1]
# 取全部行，最后一列，也就是目标值
y = data[:, -1]
print(x)
print(y)
# 创建线性回归模型
model = LinearRegression()
# 训练
model.fit(x, y)
# 权重
print("w:",model.coef_)
# 偏置
print("b:", model.intercept_)
# 预测新数据
y_pred = model.predict([[-4,10,6,4,-14,-2,-14,8]])
print(y_pred)

结果展示：

四、总结

决策树 是一种基于树形结构的分类和回归算法，通过信息增益或基尼指数进行特征选择。

随机森林 是基于决策树的集成学习方法，通过 Bootstrap 抽样和随机特征选择提高模型的泛化能力。

线性回归 是一种简单的回归模型，通过最小二乘法或梯度下降等方法求解权重参数。

希望这篇博客对你有所帮助！如果有任何问题，欢迎进一步讨论。

查看全文

http://www.dtcms.com/a/315779.html