2025年EAAI SCI1区TOP,森林救援调度与路径规划:一种新型蚁群优化算法应用,深度解析+性能实测
目录
- 1.摘要
- 2.数学模型
- 3.改进Kmeans算法
- 4.改进蚁群算法
- 5.结果展示
- 6.参考文献
- 7.代码获取
- 8.算法辅导·应用定制·读者交流

1.摘要
随着全球气候变化和人类活动影响,森林火灾的发生频率和强度不断增加,及时有效的火灾救援变得至关重要。直升机巡检作为一种预防措施显著提升了火灾事件的应对效率,但现有直升机路线规划方法通常侧重于单一阶段调度(如离线预规划或在线实时调整),难以在动态环境中平衡预定路线与实时紧急响应之间的关系。此外,传统蚁群优化算法(ACO)存在初始解过于随机和后期搜索阶段禁忌表过于严格等问题,导致算法易于过早收敛并且不稳定。因此,本文提出了一种两阶段动态路径规划模型,结合了离线预调度与在线自适应调整,该模型采用改进蚁群优化算法(IACO),对所有巡检点的路线进行优化,通过动态信息素初始化和阶段性更新策略,增强了探索与利用的平衡。在实际操作中,当紧急情况发生时,模型能够动态调度最近的可用直升机,并重新规划其余巡检路径。
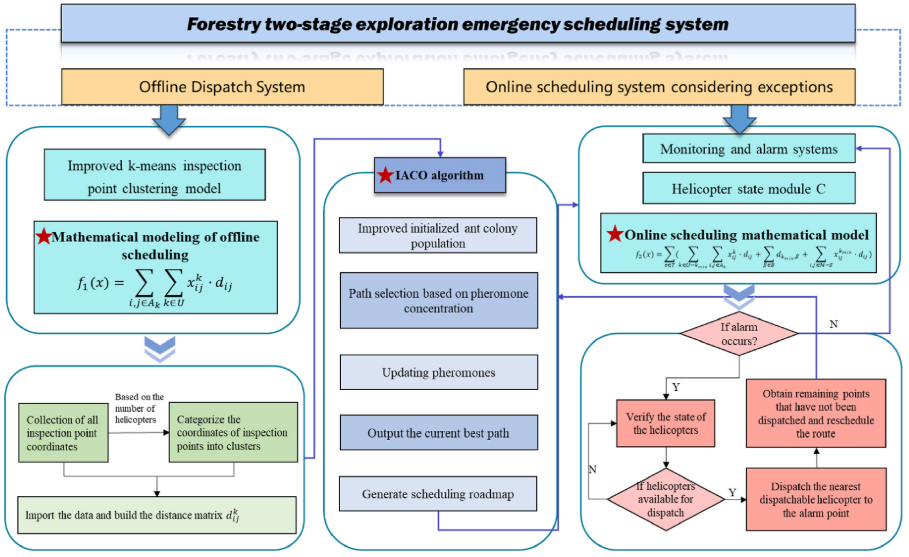
2.数学模型
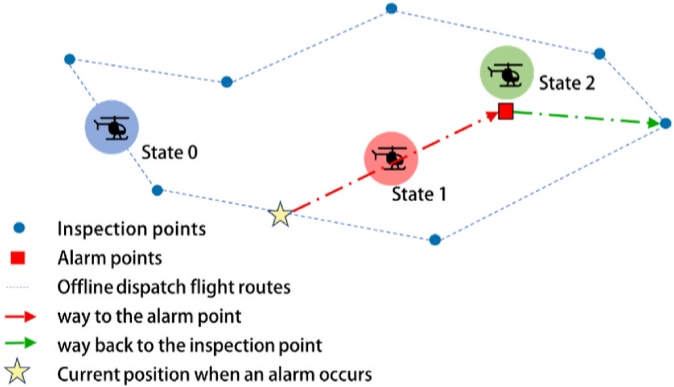
本文模型分为离线调度和在线调度两个阶段,离线调度通过聚类方法将巡查点分类,分类数量取决于直升机数量;在线调度则根据紧急情况的时间和地点,迅速调度最近直升机进行巡查。直升机的状态分为三类:正常巡逻、飞往报警点和在报警点检查。模型核心是优化直升机的巡逻路线和应急响应路径,以提高救援效率。状态之间的过渡及决策逻辑构成动态调度机制。通过重新规划飞行路线,确保直升机高效完成巡查和应急任务,该模型的两阶段动态路径规划,每个阶段有独立的目标函数,旨在提升路径规划效率和响应速度。

离线调度
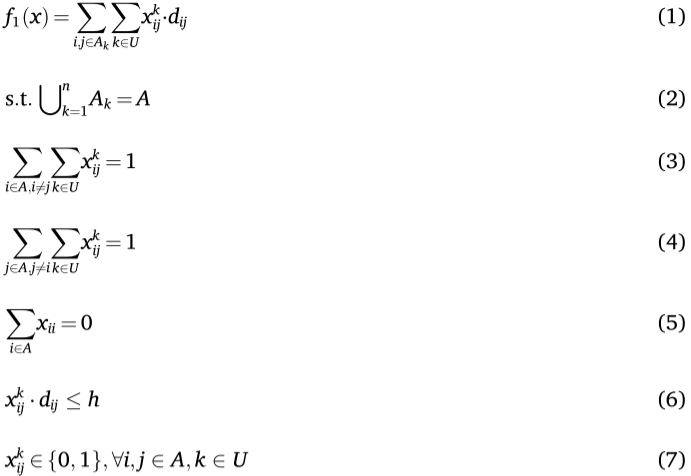
等式(1)是阶段1的目标函数,调度所有直升机的飞行路线,等式(2)-等式(7)是约束条件,确保巡查点数量、路径唯一性、飞行顺序、最大飞行距离及二进制决策变量。
在线调度


等式(8)-等式(11)为目标函数,主要包括直升机已飞行路径、从当前位置到报警点的路径和后续巡查路径。等式(12)-等式(18)定义了相关约束,确保飞行时间、直升机数量、路径长度和最大飞行距离等条件。等式(19)强调未巡查点TSP从紧急点β\betaβ开始。
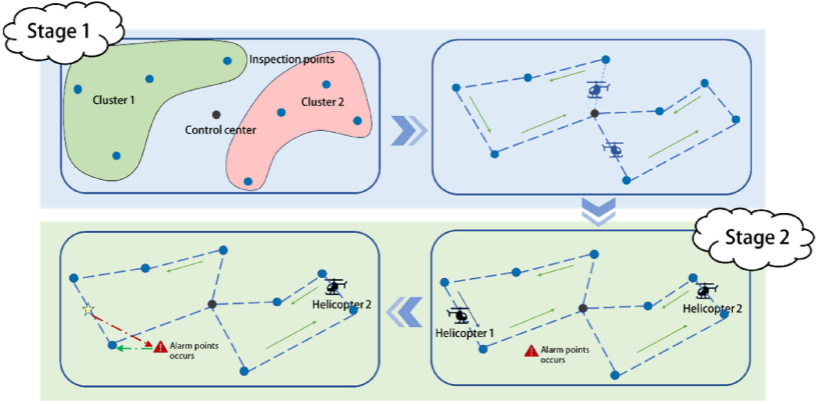
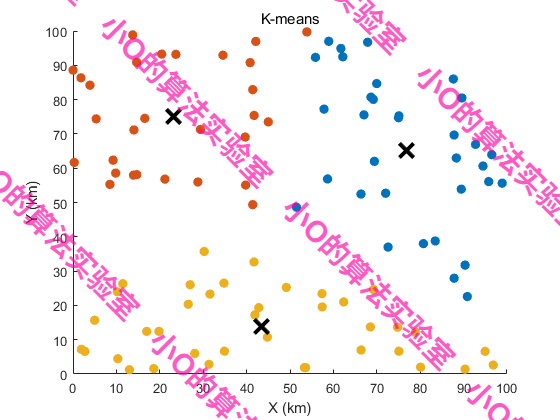
3.改进Kmeans算法
森林火灾应急响应要求快速调度,K-means算法在处理100个巡查点时效率高于层次聚类。将巡查问题转化为多个TSP问题后,K-means聚类结果更适合解决TSP问题。为提高稳定性和准确性,本文通过计算几何中心并采用距离优先启发式方法优化初始质心选择,显著提升了聚类效果与计算效率。
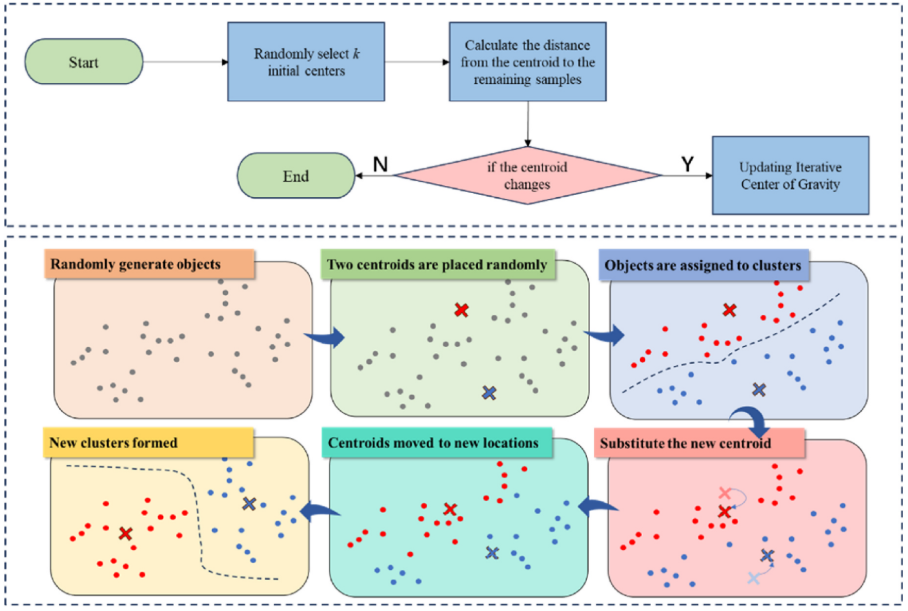

4.改进蚁群算法
信息素初始化
传统蚁群算法中,初始信息素均匀分布,导致蚂蚁在初期搜索中较为盲目。研究表明,依据节点到直线的欧几里得距离动态分配初始信息素,可以显著提高初始搜索效率。
τ0=(1+dijk−0.5)n\tau_0=\left(1+d_{ijk}^{-0.5}\right)n τ0=(1+dijk−0.5)n
信息素更新
蚂蚁的行为在现实中与算法模型不完全一致,尤其在TSP中,路径选择受到禁忌列表的限制,导致后期选择性能下降。此外,ACO中的信息素更新可能干扰后续优化。因此,本文提出了一种新策略增强巡回早期的更新强度并减少后期更新,来减少信息素对后续蚂蚁搜索的影响。
Δτijk={Q×n−s+1n(n+1)/2if ant k passes through path ij0otherwise\Delta \tau_{ij}^{k} = \begin{cases} Q \times \frac{n - s + 1}{n(n + 1)/2} & \text{if ant k passes through path ij} \\ 0 & \text{otherwise} \end{cases} Δτijk={Q×n(n+1)/2n−s+10if ant k passes through path ijotherwise
其中,nnn表示蚂蚁的总数量,sss表示蚂蚁在队列中的当前位置。这里,通过蚂蚁的遍历顺序将信息素按递减比例分布到路径上,实现了信息素递减的概念。然而固定比例分配方式在实际应用中难以达到最优性能,因此引入了最大和最小信息素更新常数Max(C)Max(C)Max(C):
Δτijk={Q×Max(C)−(n−s+1)(Max(C)−Min(C))n(n−1)(Max(C)+Min(C))if ant k passes through path ij0otherwise\Delta \tau_{ij}^{k} = \begin{cases} Q \times \frac{ \text{Max}(C) - (n - s + 1)(\text{Max}(C) - \text{Min}(C)) }{ \frac{n}{(n - 1)}(\text{Max}(C) + \text{Min}(C)) } & \text{if ant k passes through path ij} \\ 0 & \text{otherwise} \end{cases} Δτijk={Q×(n−1)n(Max(C)+Min(C))Max(C)−(n−s+1)(Max(C)−Min(C))0if ant k passes through path ijotherwise

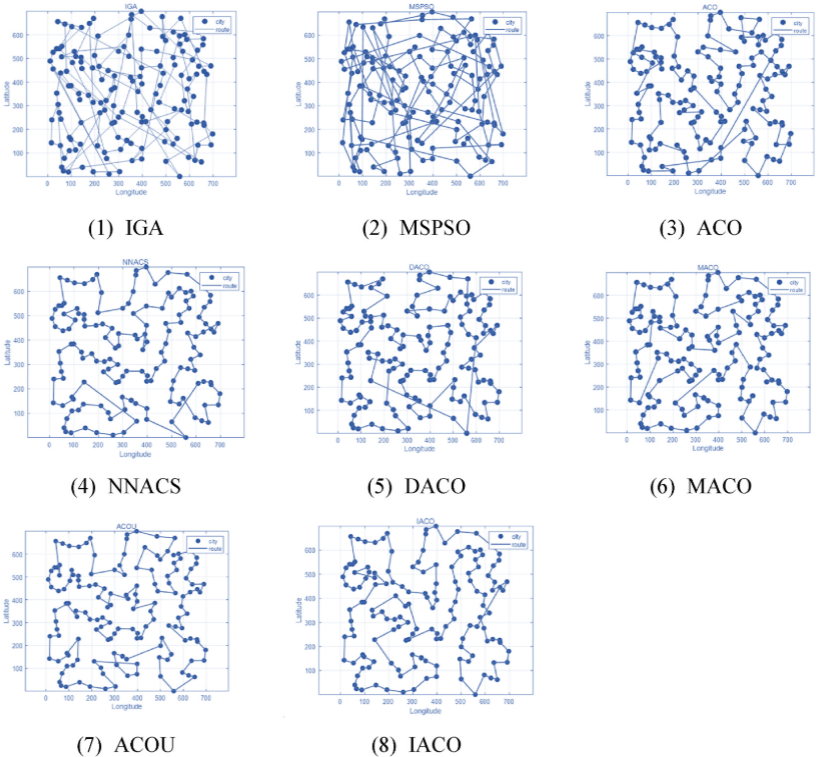
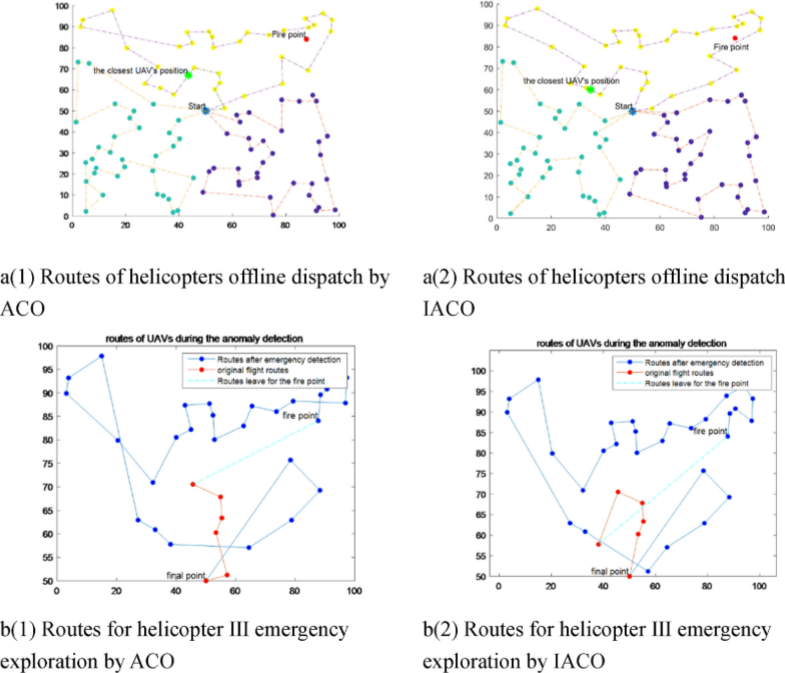
5.结果展示
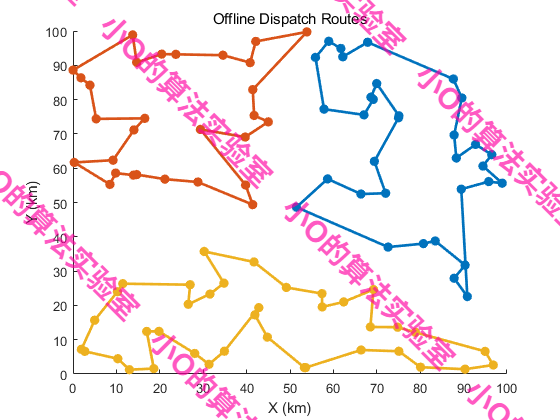
6.参考文献
[1] Wangying X, Naiming X. Scheduling and route planning for forests rescue: Applications with a novel ant colony optimization algorithm[J]. Engineering Applications of Artificial Intelligence, 2025, 155: 111042.
7.代码获取
xx
8.算法辅导·应用定制·读者交流
xx
