01数据结构-二叉搜索树
01数据结构-二叉搜索树
- 前言
- 1. 二叉搜索树(BST)的概念
- 1.1定义和性质
- 1.2二叉搜索树的优势
- 2.二叉搜索树的维护
- 3.二叉搜索树的插入
- 3.1二叉搜索树的插入逻辑
- 3.2二叉搜索树的插入代码
- 4.线性查找和二叉查找树查找快慢比较
- 5.二叉搜索树的删除
- 5.1二叉搜索树的删除逻辑
- 5.1二叉搜索树的删除代码
- 6.二叉搜索树的非递归插入
- 6.1二叉搜索树的非递归插入逻辑
- 6.2二叉搜索树的非递归插入代码
- 7.二叉搜索树的非递归删除
- 7.1二叉搜索树的非递归删除逻辑
- 7.2二叉搜索树的非递归插入代码
前言
二叉搜索树是在前面二叉树的基础上又增加了几个约束条件,没有约束的树对我们来说没有什么意义。不能解决什么问题,只能解决存储行为,为了解决进一步的需求,人们又在二叉树的基础上增加了几个规则约束。这棵树我们在工程中很少会用到,但是我们后面讲的很多树例如平衡树,红黑树。都是以这棵树为基础。大家可以看一下这个网址,里面包含了我们一些常规的难理解的一些算法的动图:链接: https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
1. 二叉搜索树(BST)的概念
二叉搜索树(Binary Search Tree),也有称之为二叉排序树、二叉查找树。排序和查找效率较高
1.1定义和性质
在二叉树的基础上,增加了几个规则约束(如图1):
- 如果他的左子树不空,则左子树上所有结点的值均小于它的根结点的值。
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值。
- 它的左、右树又分为二叉排序树。
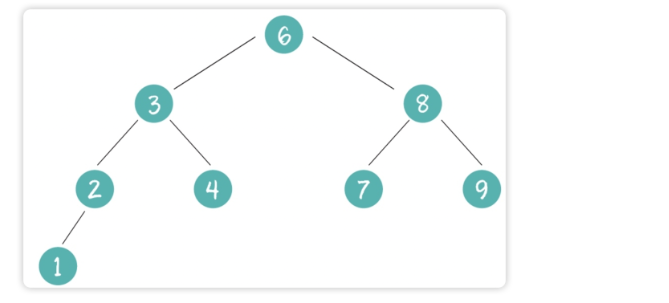
图1
1.2二叉搜索树的优势
- 查找值的效率高:在图1一共有9个数,我们知道在9个数里如果我们要查找一个数据,最差的情况就是找了9次都没找到。而在二叉搜索树中的查找效率会很高,比如我们要找16,由于16比6大,所以16绝对不会在左边,所以应该走向6的右边,而一旦走向6的右边,6的左边我们就再也不会去查找了,同理16比8大,继续往8的右边走,遇到9,发现9的右边为空,故这棵树里没有16。由此得出,每往下迈出一层都会少查找一部分子树的数据,一共查询了3次,显然这跟树的高度有关,查询的最坏情况是4次(当我们查询的数据是0的时候)比起9次我们查找的效率一下就高了,这就是为什么二叉搜索树查询效率高。
- 二叉排序树的中序遍历,就是一个从小到大排好序的序列
2.二叉搜索树的维护
我们如何维护一个二叉搜索树呢,和之前一样,我们需要知道二叉搜索树的根节点的地址,由于是二叉搜索树我们还可能想放一下别的信息,比如有多少个节点啊,int count;树的名字啊,char *name;所以这个二叉搜索树的维护还是和我们之前的逻辑一样,定义一个“树头”结构体,那以后要插入数据,只需找到树头然后“干活”就行了,所以在整个二叉搜索树中,我们的结构定义仍然是树头加树体,这个树体我们是用链式结构来存储的,既然用链式存储来存,那我们只需要知道一个点(root),根据它的左右慢慢找就行了。
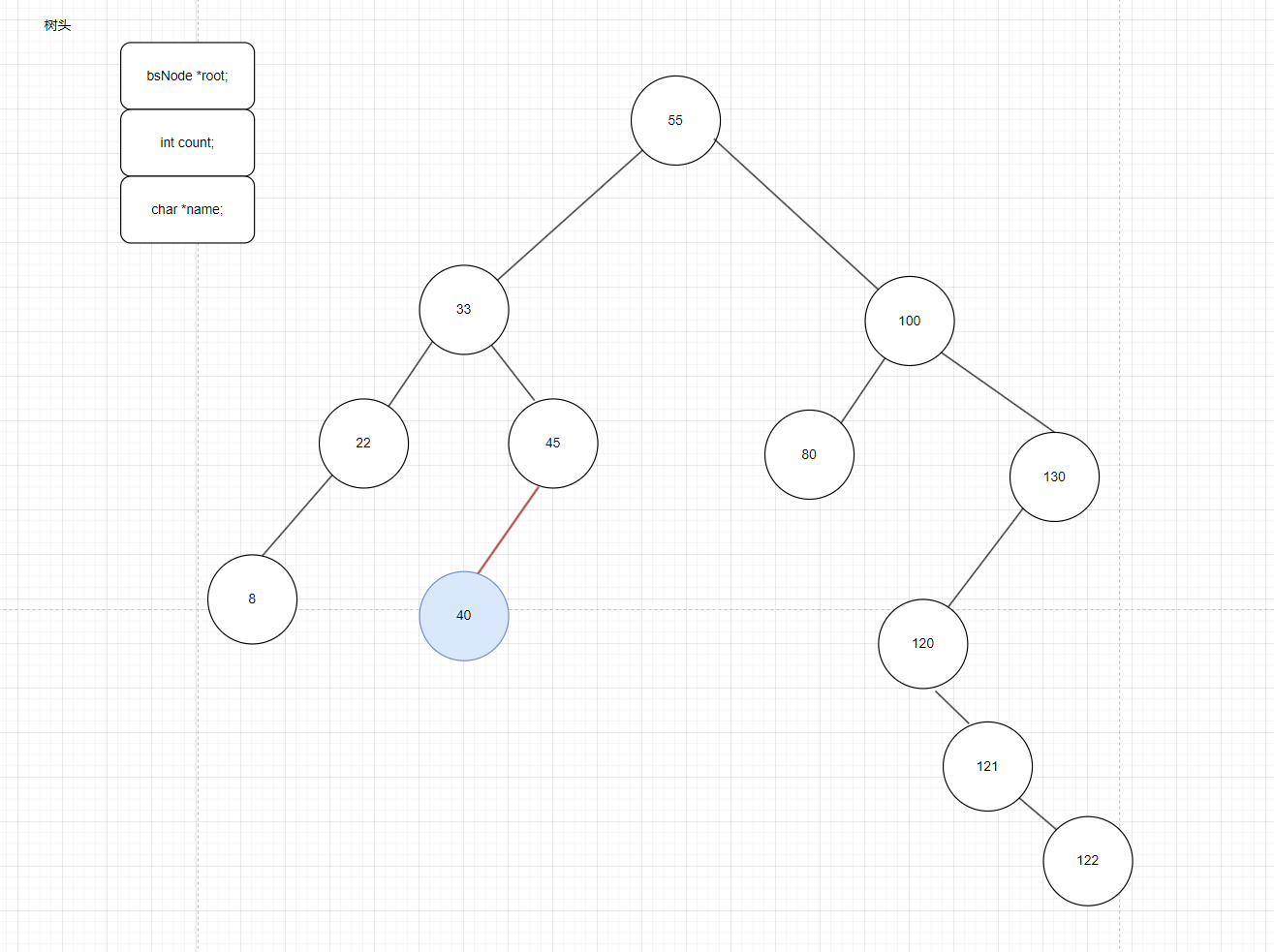
图2
3.二叉搜索树的插入
3.1二叉搜索树的插入逻辑
如图3是一颗二叉搜索树,我们要将40这个数据插入这个二叉树,有的同学会这样想40比33大又比45小,那可不可以在33和45之间横插一脚,把40放进去呢,这个想法归纳一下就是能不能在二叉搜索树的任意位置的中间插入数据呢。如果这么放会发现代码会很难写,因为会涉及很多关系的重建并且在代码角度也很难找到两个值一个比要插入的数据大一个比要插入的数据小。
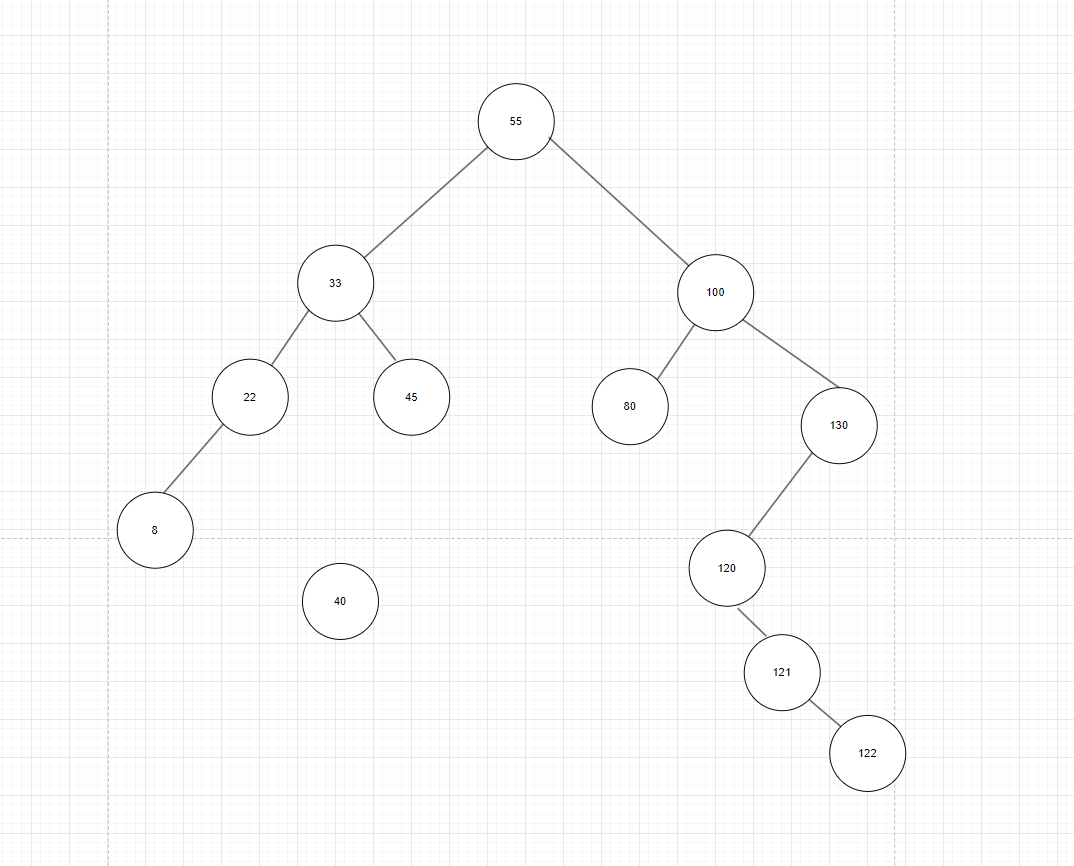
图3
二叉搜索树又叫动态树,它会根据你目前树的情况进行构建,接下来看一个极端的例子,我要把123456构建成一个二叉搜索树,发现这不是一个单链表吗,所以二叉搜索树中一个致命的问题是:所有的插入都是动态的行为,而动态行为意味着它每次插入的节点都一定在空位置上,不能在两个数据间随便插入。所以接下来看40的正确插入逻辑
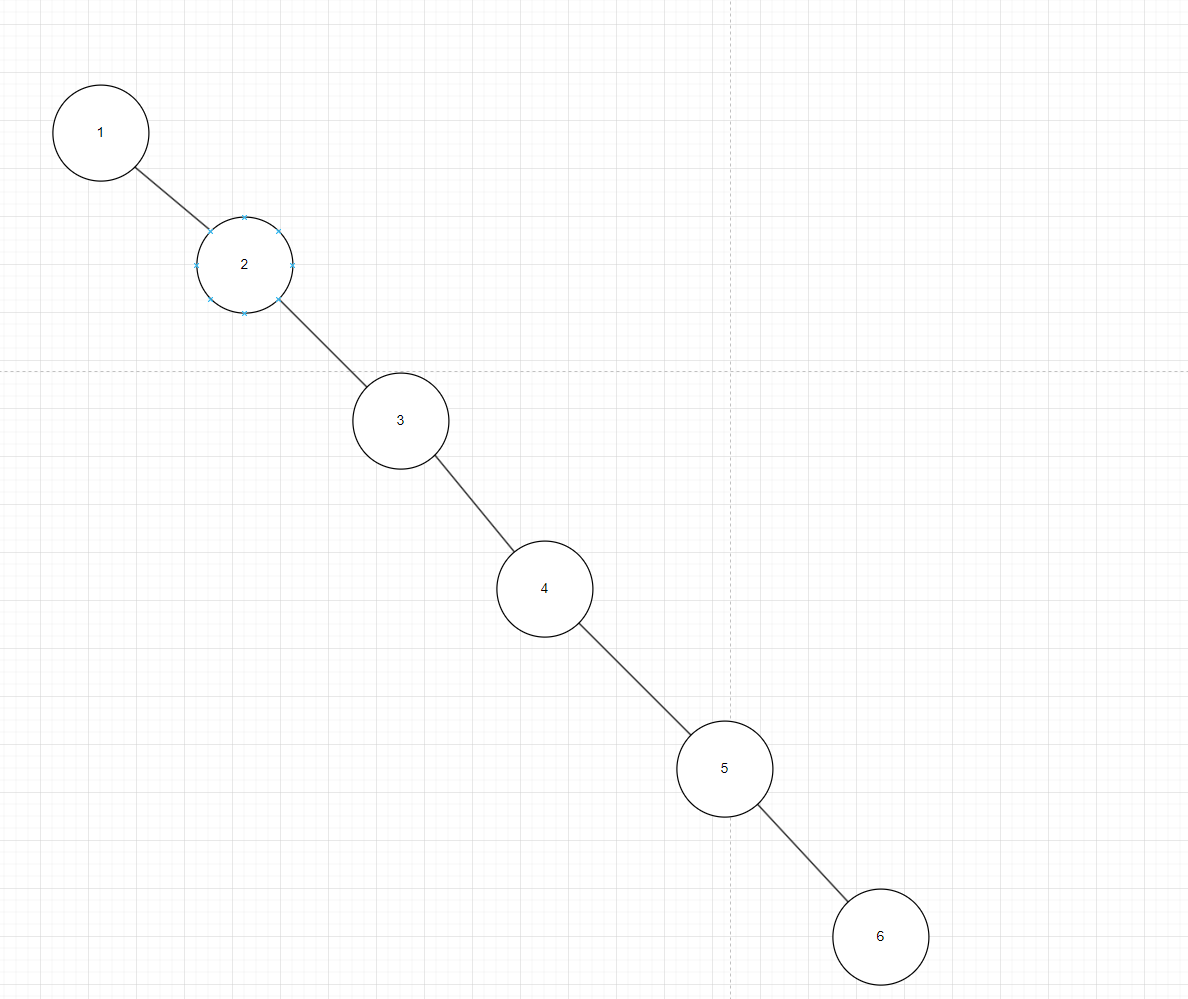
图4
如图5:从根节点开始,由于40比根节点55小,所以40在根节点的左边,来到根节点的左子树,40比33大,40应该在33的右边,来到33的右子树,40比45小,所以40应该在45的左边,来到45的左边,这时45左边为NULL,当一个任务传入了空节点就意味着应该创建一个节点,创建新节点的目的是拿着这个创建的新节点的地址归回到之前没处理完的问题(插入新节点),归回到45的时候应该归回到33,归回到33的时候又归回到根节点55,因为最终的问题是给这棵树体插入一个新元素40,所以最终是对根节点进行操作。
我们再来理一下逻辑:我们应该处理的是根节点55,只处理55,结果出不来,在55的基础上拆成33的问题,再拆成45的问题,最后发现把新节点插入到45的左边就解决问题,解决问题后就从路径原路返回到根节点。很明显这是一个递归函数,用简单的话来说,就是把大问题一直拆拆拆成很多个小问题,一直拆到临界值后,开始原路返回处理逻辑,这和我们之前讲二叉树的前,中,后序遍历的代码还不一样,之前的情况我们不需要返回值,但我们现在归回来的时候需要带着返回值进行返回,因为每返回一次会就和之前的树体不一样会得到一个新的返回情况。
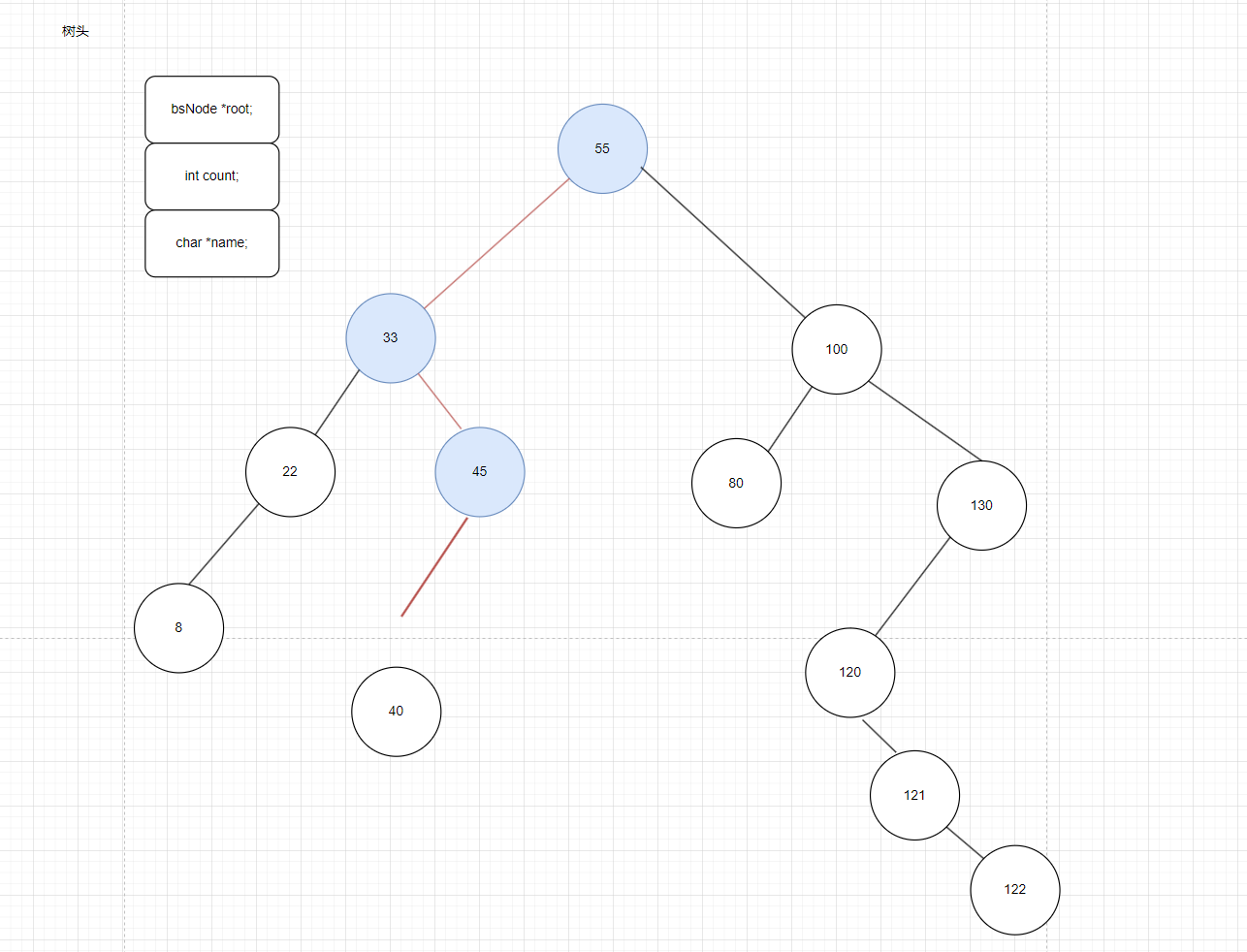
图5
总结:二叉搜索树的插入行为一定是在空位置上插入
3.2二叉搜索树的插入代码
节点和树头的创建:
typedef int Element;
// 定义二叉搜索树的节点结构
typedef struct _bs_node {Element data;struct _bs_node *left;struct _bs_node *right;
}BSNode;
// 定义二叉搜索树的头节点
typedef struct {BSNode *root;int count;char *name;
}BSTree;
//创建树头
创建树头:BSTree * createBSTree(const char *name);
BSTree * createBSTree(const char *name) {BSTree *tree=malloc(sizeof(BSTree));if (tree==NULL) {fprintf(stderr,"tree malloc failure");return NULL;}tree->name=name;tree->root=NULL;tree->count=0;return tree;
}
创建节点:static BSNode *createBSNode(Element e);
static BSNode *createBSNode(Element e) {BSNode *node = malloc(sizeof(BSNode));if (node == NULL) {return NULL;}node->data = e;node->left = node->right = NULL;return node;
}
中序遍历的代码:根据中序遍历的结果是从小到大顺序排列查看我们的插入逻辑是否正确
void visitBSNode(const BSNode *node) {printf("\t%d", node->data);
}static void inOrderBSNode(const BSNode *node) {if (node) {inOrderBSNode(node->left);visitBSNode(node);inOrderBSNode(node->right);}
}void inOrderBSTree(const BSTree *tree) {printf("[%s]Tree: ", tree->name);inOrderBSNode(tree->root);printf("\n");
}
以上的代码之前都写过,就不赘述了。接下来来看插入的代码:
——————————————————————————————————————
插入:现在归回来的时候需要带着返回值进行返回,创建新节点的目的是拿着这个创建的新节点的地址归回到之前没处理完的问题(插入新节点),我注释里是我第一遍写的代码,这个代码有两个严重的错误,一是在返回的过程中途径每一个节点不管是不是空都会创建一个新节点,但我们正确的逻辑是只在空节点的位置插入,二是返回的是原来没有更新的节点没意义,我直接返回的node,这样在 node->left=insertBSNode(tree,node->left,e);和node->right=insertBSNode(tree,node->right,e);这两句话中不会更新到上层节点,因为return的本身就是下层的节点。举个例子在图4中,当我们的node是45节点的左节点即NULL时,如果按照注释里的代码,此时跳出if(node),进入到下面三句话,创建一个新节点,树的数量加1,沿着路径返回给上一级的node,而当前node是45节点的左节点即NULL,上一级的node是45,没有起到更新节点的意义,并在当返回后,在45这个节点又会创建一个新节点,一直返回到根节点,这些创建的新节点没有和树中的节点产生联系,没有free掉还会造成内存泄露,正确的逻辑我已写在下面。
static BSNode *insertBSNode(BSTree *tree,BSNode *node,Element e) {// if (node) {// if (e<node->data) {// node->left=insertBSNode(tree,node->left,e);// }// if (e>node->data) {// node->right=insertBSNode(tree,node->right,e);// }// }//入的时候不会创建节点但是在返回的过程中途径每一个节点时都会创建一个新节点//返回的是原来没有更新的节点没意义// BSNode *new_node=createBSNode(e);// tree->count++;// return node;if (node == NULL) {tree->count++;return createBSNode(e);}if (e < node->data) {node->left = insertBSNode(tree, node->left, e);} else if (e > node->data) {node->right = insertBSNode(tree, node->right, e);}return node;
}void insertBSTree(BSTree *tree, Element e) {tree->root=insertBSNode(tree,tree->root,e);
}
计算树的高度:计算树的高度就要先计算每个节点的高度,所以这里依旧采用内在接口先计算节点的高度把根节点传入进去即可。注意到要想计算一个节点的高度,我们可以把它拆成计算它得子树的高度,然后发现又可以拆分,一直到为空的时候,从叶子节点开始加高度,所以这里很明显也是一个递归函数,我们将其分为左子树和右子树:
- 1.如果节点是NULL,返回0(空树高度为0)
- 2.递归计算左子树的高度。
- 3.递归计算右子树的高度。
- 4.比较左子树高度和右子树高度,选择较大的那个,然后加1(因为要加上当前节点自身的一层)并返回。
注意:返回的是以当前节点为根的子树的高度(节点数定义的高度:从当前节点到最远叶子节点的节点个数,包括当前节点和叶子节点。所以空节点返回0,叶子节点返回1。这里简单举个例子:
如图6:计算节点高度(从下向上):
-
叶子节点
D和E:- 左右子树均为
NULL→leftHeight = 0,rightHeight = 0 - 返回
max(0, 0) + 1 = 1
- 左右子树均为
-
节点
B:- 左子树高度 =
height(D) = 1 - 右子树高度 =
height(NULL) = 0 - 返回
max(1, 0) + 1 = 2
- 左子树高度 =
-
节点
C:- 左子树高度 =
height(NULL) = 0 - 右子树高度 =
height(E) = 1 - 返回
max(0, 1) + 1 = 2
- 左子树高度 =
-
根节点
A:- 左子树高度 =
height(B) = 2 - 右子树高度 =
height(C) = 2 - 返回
max(2, 2) + 1 = 3
- 左子树高度 =
最终结果:
A的高度 = 3B/C的高度 = 2D/E的高度 = 1
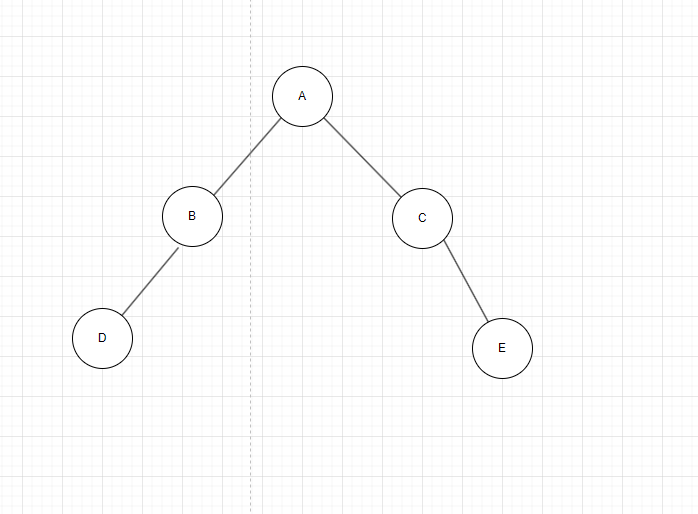
图6
static int heightBSNode(const BSNode* node) {if (node==NULL) {return 0;}int leftHeight=heightBSNode(node->left);int rightHeight=heightBSNode(node->right);if (leftHeight > rightHeight) {return ++leftHeight;}return ++rightHeight;
}int heightBSTree(const BSTree *tree) {return heightBSNode(tree->root);
}
最后来测试一下:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "binarySearchTree.h"void test01() {int data[] = {55, 33, 100, 22, 80, 45, 130, 8, 120, 40, 121};BSTree *tree = createBSTree("stu01");if (tree == NULL) {return;}for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {insertBSTree(tree, data[i]);}inOrderBSTree(tree);printf("Tree node :%d, height: %d\n", tree->count, heightBSTree(tree));
}
int main() {test01();return 0;
}
大家看一下这里 sizeof(data) / sizeof(data[0],这种方式表示数组中的元素个数挺有意思的。
结果:
D:\work\DataStruct\cmake-build-debug\02_TreeStruct\BSTree.exe
[stu01]Tree: 8 22 33 40 45 55 80 100 120 121 130
Tree node :11, height: 5进程已结束,退出代码为 04.线性查找和二叉查找树查找快慢比较
二分查找树的查找代码:BSNode *searchBSTree(const BSTree *tree, Element e);
BSNode *searchBSTree(const BSTree *tree, Element e) {BSNode *node = tree->root;while (node != NULL) {if (e == node->data) {return node;} else if (e < node->data) {node = node->left;} else {node = node->right;}}return NULL;
}
这个代码比较简单我就不过多赘述。下面来看一下测试案例:
//线性查找
static void linearFindTest(const Element *data, size_t n, int cnt, Element value) {for (int i = 0; i < cnt; ++i) {for (int j = 0; j < n; ++j) {if (data[i] == value) {printf("!!!Linear Find!!!\n");return;}}}
}
//二分搜索树查找
static void binaryFindTest(BSTree *tree, int cnt, Element value) {BSNode *node = NULL;for (int i = 0; i < cnt; ++i) {node = searchBSTree(tree, value);if (node) {printf("!!! BSTree Find!!!\n");return;}}
}void test02() {// size_t是一个在 C 和 C++ 标准库中定义的无符号整数类型// 通常用于表示内存大小、数组索引和循环计数器等// <-----------------数据初始化---------------->size_t n = 100000;int cnt = 10000;Element m = n + 5000;// 创建n个元素,取值范围在1 ~ m之间Element *data = malloc(n * sizeof(Element));srand(time(NULL));for (int i = 0; i < n; i++) {data[i] = rand() % m + 1;}// <-----------------线性查找----------------->// `clock_t start = clock();`// 这行代码用于在 C 或 C++ 程序中记录程序的开始时间。// 单位是 `CLOCKS_PER_SEC`(每秒的时钟滴答数)。clock_t start = clock();linearFindTest(data, n, cnt, m + 5);// 记录程序结束时间clock_t end = clock();printf("Linear Find time: %lf sec\n", (double)(end - start) / CLOCKS_PER_SEC);// <-----------------二分搜索树的查找----------------->BSTree *tree = createBSTree("stu02");for (int i = 0; i < n; ++i) {insertBSTree(tree, data[i]);}printf("tree height: %d\n", heightBSTree(tree));start = clock();binaryFindTest(tree, cnt, m + 5);end = clock();printf("binaryFind time: %lf sec\n", (double)(end - start) / CLOCKS_PER_SEC);free(data);
}
先讲void test02()
- 数据初始化:
n代表我们的数据的个数cnt代表我们查询的次数m代表这n个数的取值范围。srand(time(NULL)):这行代码初始化随机数生成器的种子。time(NULL)返回当前时间(以秒为单位),这样每次运行程序时都会得到不同的随机数序列。for (int i = 0; i < n; i++):这个循环遍历n次,生成n个随机数。data[i] = rand() % m + 1:这行代码生成一个从 1 到m的随机数,并将其存储在data数组中。rand()生成一个介于 0 和RAND_MAX之间的随机整数,rand() % m将其限制在 0 到m-1之间,再加上 1 就得到了 1 到m之间的随机数。
为了防止我们运气好一开始就找到value,我们将value的值设置为m+5,这样由于n的范围是1-m,我们在找到value之前,cnt是一定能执行完的。
- 线性查找
- 插入n个元素,记录时间。在linearFindTest里面一次太快了,循环cnt次。
- 二分搜索树的查找
- 同样插入n个元素,记录时间
- 同样为了防止太快binaryFindTest,循环cnt次
最后来测试一下结果:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "binarySearchTree.h"int main() {//test01();test02();return 0;
}
结果:
D:\work\DataStruct\cmake-build-debug\02_TreeStruct\BSTree.exe
Linear Find time: 0.512000 sec
tree height: 38
binaryFind time: 0.001000 sec进程已结束,退出代码为 0
你可以看到二分搜索树查找比线性查找快很多,因为这里生成的树的高度是38,按之前讲的理论即最多找38次就知道有没有找到了,而线性查找要一次一次地找。但这并不是说可以淘汰线性查找了,如果我频繁地用下标来查找,那线性表这时就比二分搜索树查找快了。
5.二叉搜索树的删除
5.1二叉搜索树的删除逻辑
写代码满足逻辑完备性(所有情况都要考虑进去):且删除后的树依旧是二叉搜索树
- 删除度为0的点:
- 如图7,叶子结点从二叉搜索树中移除后,并不影响其他结点的排列规则,直接删除
- 删除度为1的点:
- 例如我们要删除22,那能不能简单地直接把22和他的左子树一起删了呢?肯定是不行的,我们只是删除22,并不删除8。我们要删22,看33的左边,33的左边一定是比33小的,由于度为1,我们直接把8这个节点连在33的左边即可
- 该节点缺失左子树或右子树,当去掉这个节点后,剩余的左子树和右子树满足二叉搜索树的要求
- 矛盾在于删除的这个节点,属于父节点的左边还是右边,那么剩余的左子树或右子树仍然满足父节点的左右属性,接
入这个父节点就可以
度为0和度为1的代码都挺容易的我们可以把它归纳成一个代码。
情况一:如果一个节点的左边为空,那么它要么是度为0的点,要么是度为1的点,那我们只需判断如果左边的点为空,那我们直接把右边的子树(若为空也成立)替换过去就行了。
情况二:如果一个节点的右边为空,那么它只能是度为1 的点,那我们直接把左边的子树(若为空也成立)替换过去就行了(左子树为空的情况在前面情况一已处理)。
- 删除度为2的点:
- 如果要删55,那我们就不知道用33替换还是用100替换,好像怎么替换都不对,这个时候可以用到我们计算机中的一个思想:转移矛盾。在删除度为0和度为1的点时,我们发现特别好做,但现在度为2的点删除很困难。此时我们删除55后,那整个树的中序遍历应该还是有序的,这棵树的中序遍历序列是:8 22 33 45
5580 100 120 121 122 130,若删除55中序遍历序列号应该是:8 22 33 45 80 100 120 121 122 130,55的前驱和后继分别是45,80,而45和80都是度为0或度为1的点。若删除100发现80和120是100的前驱和后继,也是度为0或度为1的点。那我们思考一下为什么? - 因为如果你要删除的是度为2的点,而中序遍历中以一个节点的前驱和后继一定分别是前面几个元素中最大的元素和后面几个元素中最先的元素,对应到二叉搜索树里就是要删除的这个节点的左节点的极右值和删除的这个节点的右节点的极左值。而这两个节点肯定是度为0或度为1的节点了
- 所以我们就想到要是能转换成删叶子节点就好了,这棵树的中序遍历序列是:8 22 33 45 55 80
100120 121 122 130假设我们此时要删除100,100的前驱和后继分别是80和120,我们把100替换成120,8 22 33 45 55 80120120 121 122 130,再删除120就好了,这样就不会出现两个叉不知道该链接哪一个的问题,并且中序遍历的序列还是对的。(替换成80也可以,总之是中序遍历中前驱或后继节点的替换) - 转移矛盾,把度为2的节点转换成中序遍历中前驱或后继节点的删除。前驱节点或后继节点度非0即1。
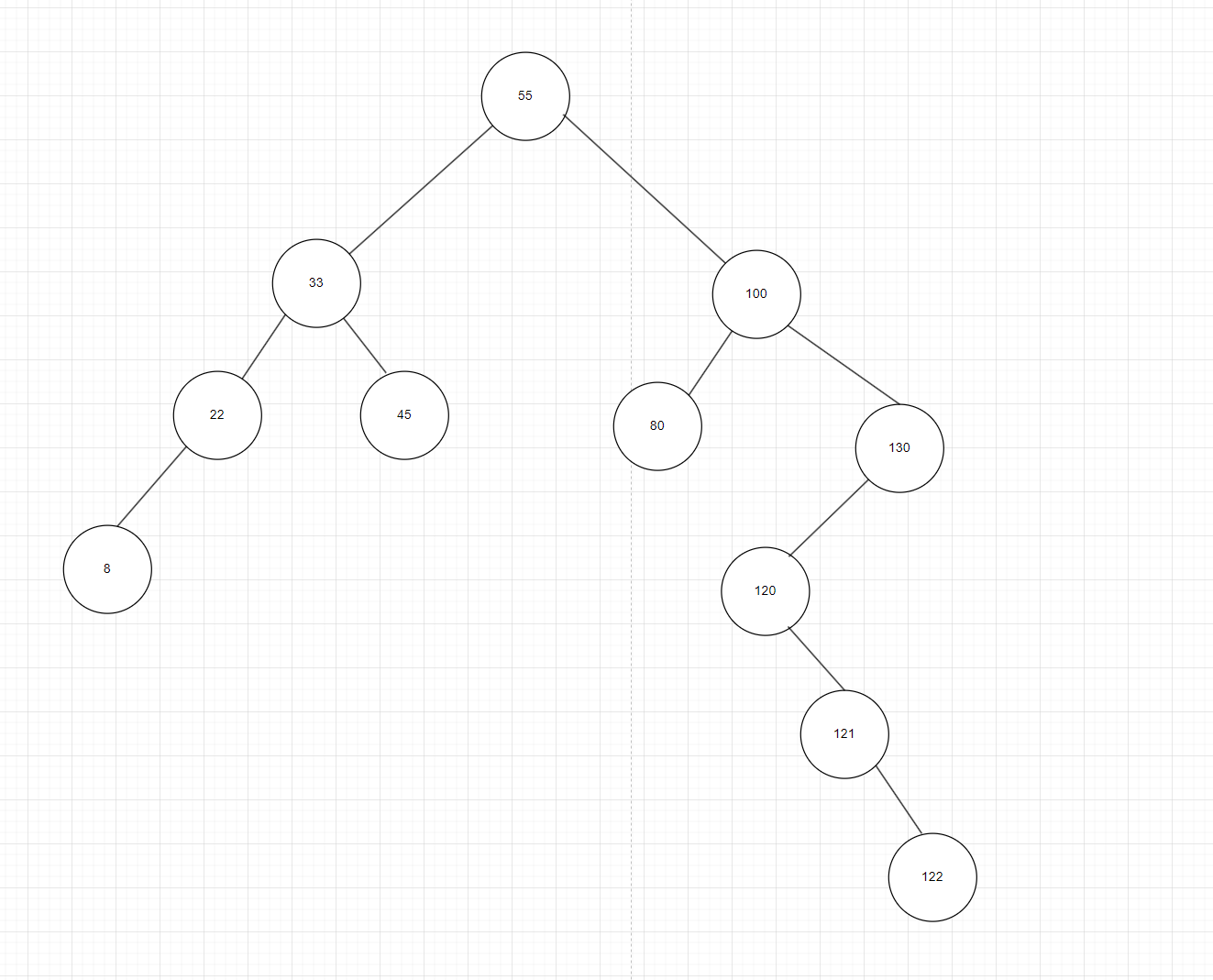
图7
- 如果要删55,那我们就不知道用33替换还是用100替换,好像怎么替换都不对,这个时候可以用到我们计算机中的一个思想:转移矛盾。在删除度为0和度为1的点时,我们发现特别好做,但现在度为2的点删除很困难。此时我们删除55后,那整个树的中序遍历应该还是有序的,这棵树的中序遍历序列是:8 22 33 45
5.1二叉搜索树的删除代码
删除代码:我们删除的是node,而不是树,只是要不删除完后子树返给tree->root,所以我们依然要定义一一个内在接口删除节点:
static BSNode *deleteBSNode(BSTree *tree,BSNode *node,Element e)
static BSNode *deleteBSNode(BSTree *tree,BSNode *node,Element e) {if (node == NULL) {return NULL;}if (node->data==e) {BSNode *tmp;if (node->left==NULL){ //度为0或1tmp=node->right;free(node);--tree->count;return tmp; }else if (node->right == NULL) { // 度为1tmp = node->left;free(node);tree->count--;return tmp;}BSNode *node_left=node->left; //度为2while (node_left->right) {node_left = node_left->right;}//deleteBSNode(tree,node_left,e);node->data=node_left->data;node->left=deleteBSNode(tree,node->left,node->data);}if (e<node->data) {node->left=deleteBSNode(tree,node->left,e);}else if (e>node->data) {node->right=deleteBSNode(tree,node->right,e);}return node;
}void deleteBSTree(BSTree *tree, Element e) {tree->root=deleteBSNode(tree,tree->root,e);
}
删除度为1和度为0的节点大家应该都看得懂,我这儿就只说删除度为2的节点的代码逻辑:
在前面我已经处理了删除度为0和度为1的节点的代码逻辑,所以这里我定义一个局部变量让他拿到前驱节点的地址(大家写的时候也可以写写成后继,大体逻辑是一样的),然后把前驱节点中的数据域赋给要删除的节点的数据域吗,最后再以node->left为起始节点删除前驱节点的值,由于前驱节点必定是度为0或1的节点,所以进入递归函数的处理逻辑阶段的时候会执行前面两段代码中的一段,最终把结果返给node->left。
BSNode *node_left=node->left; //度为2while (node_left->right) {node_left = node_left->right;}//deleteBSNode(tree,node_left,e);node->data=node_left->data;node->left=deleteBSNode(tree,node->left,node->data);
这里我说一下我最开始犯的毛病,在删除度为2的节点的时候我直接写的是:deleteBSNode(tree,node_left,e);
- 错误一:删除的目标值不对
e 是原节点要删除的值,而我们现在需要删除的是前驱节点(node_left),它的值是 node_left->data,而非 e。
如果用 e 作为参数,函数会在子树中搜索值为 e 的节点,但前驱节点的值 node_left->data 一定不等于 e(BST 中节点值唯一,且前驱是左子树最大值,小于当前节点值 e)。
结果:找不到要删除的节点,前驱节点不会被删除,导致内存泄漏,且树中会保留重复值(原节点已被替换为前驱的值,前驱本身还在)。 - 错误二:搜索的起始节点不对
node_left 是前驱节点本身,而我们需要从当前节点的左子树(node->left) 开始搜索并删除前驱节点。
如果直接传入 node_left 作为起始节点,函数会从前驱节点开始搜索,但前驱节点的子树中(如果有)不可能有 e(理由同上),且前驱节点本身的值也不是 e。
结果:递归会在 node_left 的子树中无效搜索,最终返回 NULL 或原节点,导致前驱节点始终未被删除。
最后来测一下:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "binarySearchTree.h"void test01() {int data[] = {55, 33, 100, 22, 80, 45, 130, 8, 120, 40, 121};BSTree *tree = createBSTree("stu01");if (tree == NULL) {return;}for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {insertBSTree(tree, data[i]);}inOrderBSTree(tree);printf("tree root: %d\n", tree->root->data);printf("Tree node :%d, height: %d\n", tree->count, heightBSTree(tree));deleteBSTree(tree,55);inOrderBSTree(tree);printf("tree root: %d\n", tree->root->data);int main() {test01();//test02();return 0;
}
}结果:
D:\work\DataStruct\cmake-build-debug\02_TreeStruct\BSTree.exe
[stu01]Tree: 8 22 33 40 45 55 80 100 120 121 130
tree root: 55
Tree node :11, height: 5
[stu01]Tree: 8 22 33 40 45 80 100 120 121 130
tree root: 45进程已结束,退出代码为 0
6.二叉搜索树的非递归插入
6.1二叉搜索树的非递归插入逻辑
在讲链表的时候我们讲过,只要是进行插入就应该站在插入的位置的前一个位置,这样就可以插入了,所以我们这里就了定义一个辅助指针node,假设我们要插入的是7,很明显应该在8的左边,如果我们的node指向7,那我们就没法找其父节点的地址,无法进行插入。这里采用的思想是“大哥小弟”的思想,我们设置两个辅助指针,一个cur一个pre,pre始终紧跟着cur,初始时cur指向根节点,pre指向空,当cur这个大哥每往前走一步,prev这个小弟的就备份它,当cur指向空,pre就指向了这个空的父节点,这样就可以进行插入了,如图9。但这里要注意一个点,当树本来就为空的时候,cur一返回就需要返回新节点。
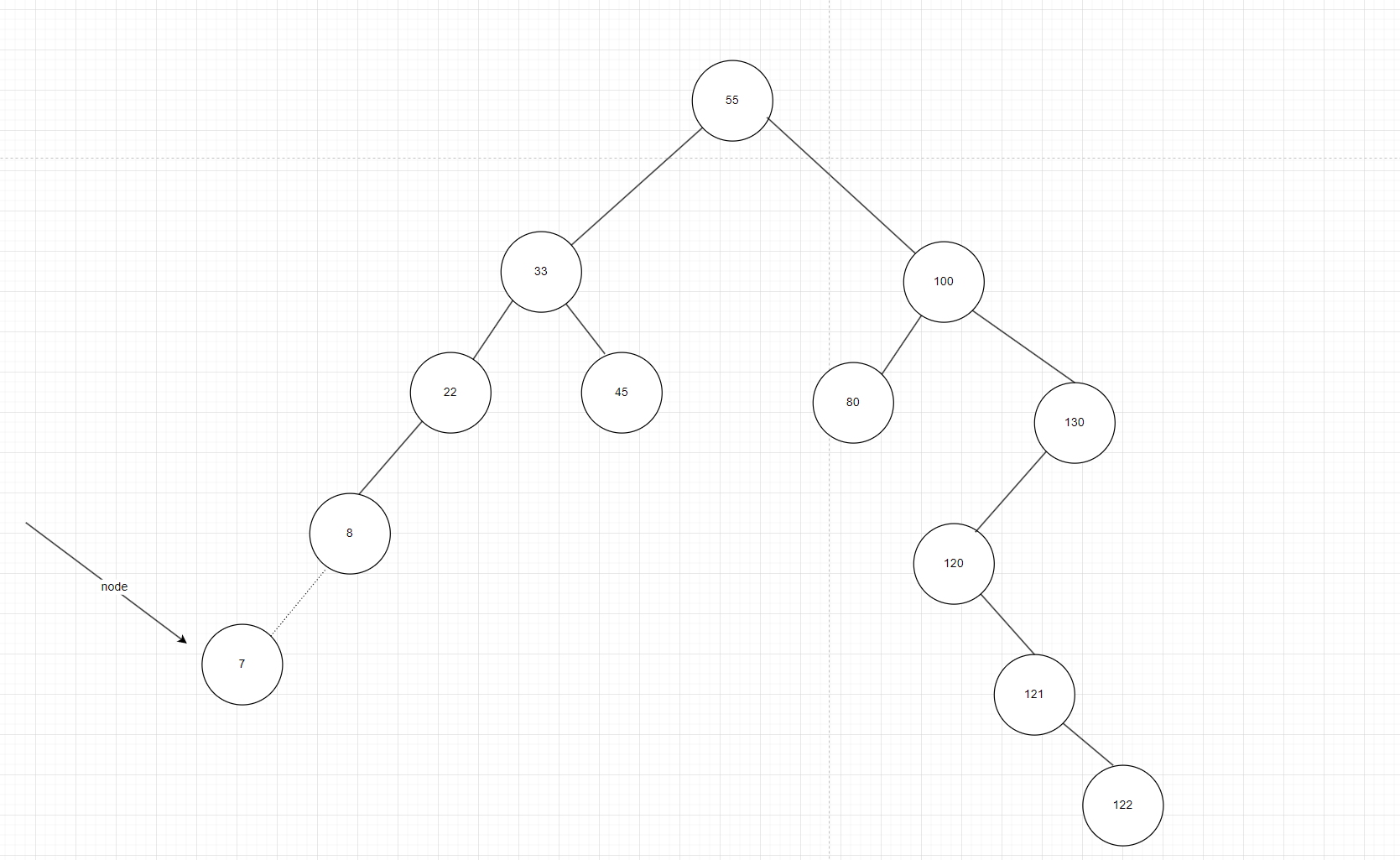
图8
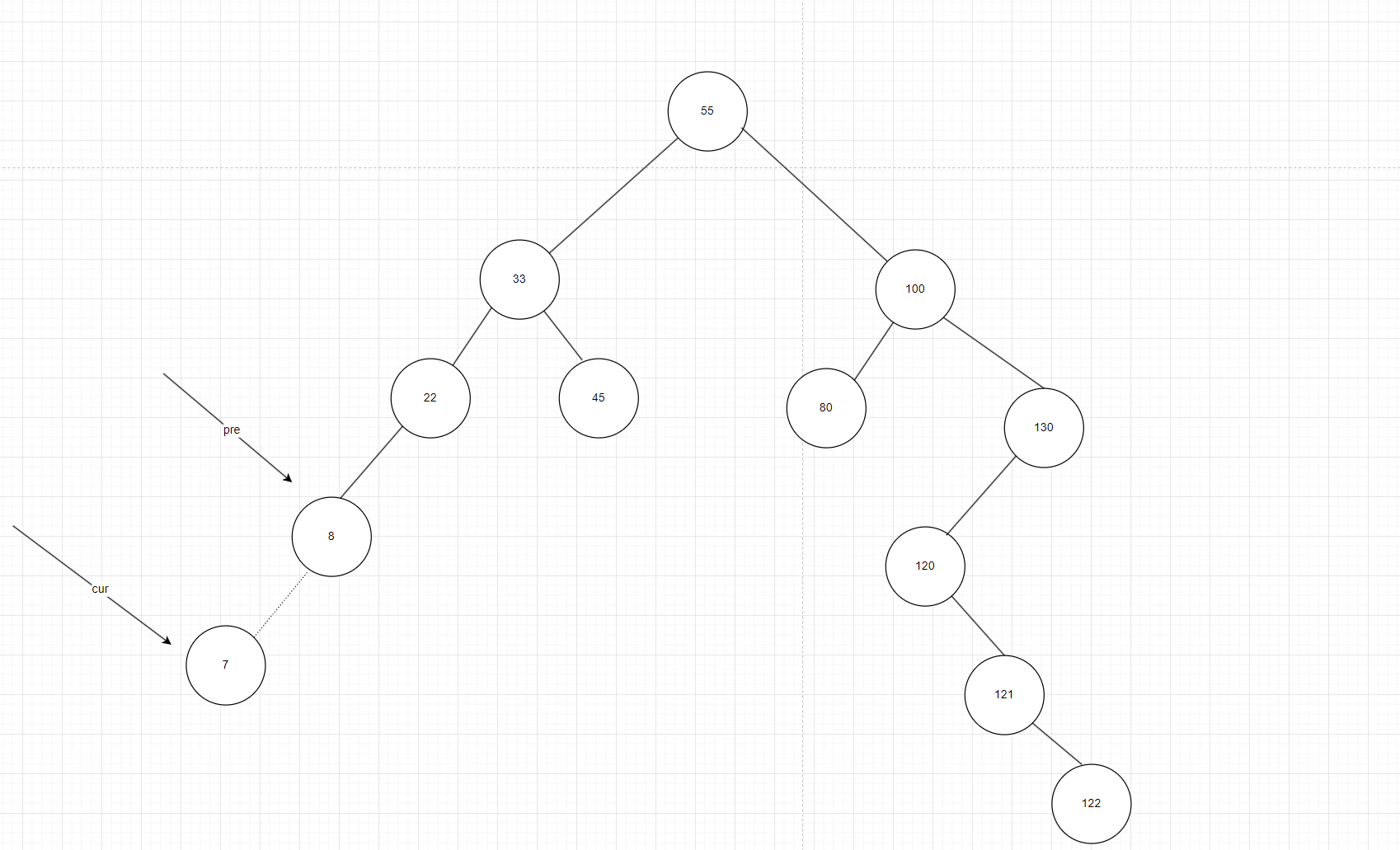
图9
6.2二叉搜索树的非递归插入代码
非递归插入:void insertBSTree(BSTree *tree, Element e);
void insertBSTree(BSTree *tree, Element e) {
#ifdef RECUR//递归调用tree->root=insertBSNode(tree,tree->root,e);
#else//非递归函数BSNode *cur=tree->root;BSNode *pre=NULL;while (cur) {pre = cur;if (e < cur->data) {cur = cur->left;} else if (e > cur->data) {cur = cur->right;}}// 可能插入的是第一个根元素,可能插入的是一个普通的位置BSNode *node = createBSNode(e);if (pre) {if (e < pre->data) {pre->left = node;} else if (e > pre->data) {pre->right = node;}} else {tree->root = node;}tree->count++;
#endif
}
其实这个函数写进static BSNode *insertBSNode(BSTree *tree,BSNode *node,Element e);也是可以的,只是稍稍改一下逻辑即可,大家应该都能看懂我就不过多赘述。
最后测一下:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "binarySearchTree.h"void test01() {int data[] = {55, 33, 100, 22, 80, 45, 130, 8, 120, 40, 121};BSTree *tree = createBSTree("stu01");if (tree == NULL) {return;}for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {insertBSTree(tree, data[i]);}inOrderBSTree(tree);printf("tree root: %d\n", tree->root->data);printf("Tree node :%d, height: %d\n", tree->count, heightBSTree(tree));deleteBSTree(tree,55);inOrderBSTree(tree);printf("tree root: %d\n", tree->root->data);
}int main() {test01();//test02();return 0;
}
结果:
D:\work\DataStruct\cmake-build-debug\02_TreeStruct\BSTree.exe
[stu01]Tree: 8 22 33 40 45 55 80 100 120 121 130
tree root: 55
Tree node :11, height: 5
[stu01]Tree: 8 22 33 40 45 80 100 120 121 130
tree root: 45进程已结束,退出代码为 0
7.二叉搜索树的非递归删除
7.1二叉搜索树的非递归删除逻辑
同样也分度为0,1,2的节点的删除,和上次写的一样,我们把度为0和1的节点删除的代码逻辑写在一起,因为不能递归所以把度为2的节点的删除单独封装一个函数进行删除
- 删除度为0或1的节点:
- 我们依旧定义两个指针,一个cur初始化为tree->root,一个pre初始为NULL,cur去寻找要删除的元素的地址,pre紧跟在cur身后, 如图10,不管我删除22还是45,pre指针都指向他们的父节点45。根据前面递归的删除逻辑:
- 情况一:如果一个节点的左边为空,那么它要么是度为0的点,要么是度为1的点,那我们只需判断如果左边的点为空,那我们直接把右边的子树(若为空也成立)替换过去就行了。
情况二:如果一个节点的右边为空,那么它只能是度为1 的点,那我们直接把左边的子树(若为空也成立)替换过去就行了(左子树为空的情况在前面情况一已处理)。
- 情况一:如果一个节点的左边为空,那么它要么是度为0的点,要么是度为1的点,那我们只需判断如果左边的点为空,那我们直接把右边的子树(若为空也成立)替换过去就行了。
- 如果我删除的是22,那么应该把22的左节点8连在pre的左边,如果我删除的是45,那么应该把45右边给pre的右边,所以这里不仅要判断删除节点的度数还要判断删除节点与pre元素的大小关系。
- 我们依旧定义两个指针,一个cur初始化为tree->root,一个pre初始为NULL,cur去寻找要删除的元素的地址,pre紧跟在cur身后, 如图10,不管我删除22还是45,pre指针都指向他们的父节点45。根据前面递归的删除逻辑:
- 删除度为2的节点:
- 在递归版中我们找的是前驱元素,这里我们就找删除后继元素,这里分两种情况,一是删除节点的右节点无极左值(即右节点的左节点为NULL),二是删除节点的右节有无极左值。
- 情况一:假设我们删除的是33,那我们应该找的是33的右边的极左值,发现45的左边为空,所以我们应该直接把45的值赋给33,然后把45的左节点即NULL连在33的右边。free(45)
- 情况二:假设我们删除的是55,那我们应该找的是55的右边的极左值为80,将80的值赋给55,然后把80的左节点即NULL连在100的左边。free(80)
- 可能会有人询问为什么之前递归函数中为什么不分这种情况,是因为递归函数通过 “函数返回值” 隐式传递了 “子树更新后的根节点”,而上层节点只需用这个返回值更新自己的 left 或 right 指针,而非递归版本中需要手动跟踪父节点(pre)并判断其与子节点关系的复杂逻辑。
- 在递归版中我们找的是前驱元素,这里我们就找删除后继元素,这里分两种情况,一是删除节点的右节点无极左值(即右节点的左节点为NULL),二是删除节点的右节有无极左值。
接下来来看代码,在代码中再详细讲述一下
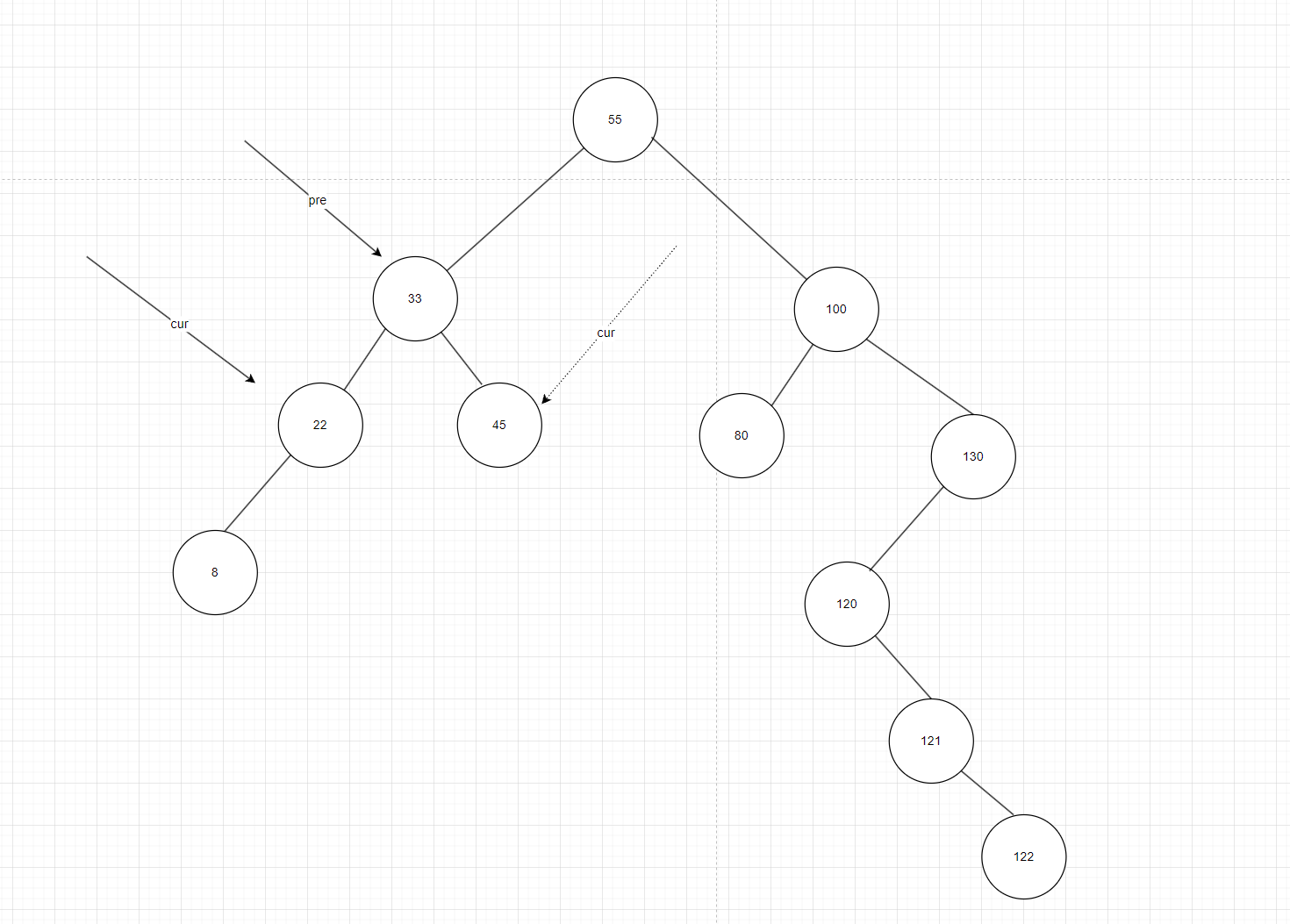
图10
7.2二叉搜索树的非递归插入代码
先来看一下释放函数的代码:
static void freeBSNode(BSTree *tree, BSNode *node) {if (node) {freeBSNode(tree, node->left);freeBSNode(tree, node->right);free(node);tree->count--;}
}void releaseBSTree(BSTree* tree) {if (tree) {freeBSNode(tree, tree->root);printf("There are %d nodes.\n", tree->count);free(tree);}
}
这里应该比较简单我就不说了。注意要用后序删除,不然会出错,原因是如果采用先序,先删除节点后,节点的左右找不到了,中序也一样的道理。
单独处理度为2的节点:static void deleteMiniNode(BSNode *node);
static void deleteMiniNode(BSNode *node) {BSNode *node_right = node->right;BSNode *pre = node;while (node_right->left) {pre = node_right;node_right = node_right->left;}// 删除最小节点if (pre->data == node->data) {// 最小节点就是右子节点pre->right = node_right->right;} else {// 最小节点不是右子节点pre->left = node_right->left;}node->data = node_right->data;free(node_right);
}
如果没有下面这个判断,即情况一,node_right->left会为NULL,不会执行while循环,此时 pre 是 node,node_right 是 node->right,本应更新 pre->right,却错误地更新 pre->left(即 node->left)。这会导致 node 的左子树被意外修改(可能被设为 NULL),并且free后没有更细node的right,导致node依然指向node_right,而node_right已被free,所以node指的是悬空的指针,导致node右子树断连,彻底破坏了树的结构,并且而递归函数会根据路径带着返回值一直更新上层节点。
if (pre->data == node->data) {// 最小节点就是右子节点pre->right = node_right->right;}
非递归删除:void deleteBSTree(BSTree *tree, Element e);
void deleteBSTree(BSTree *tree, Element e) {
#ifdef RECUR//递归调用tree->root=deleteBSNode(tree,tree->root,e);
#else//非递归函数BSNode *cur=tree->root;BSNode *pre=NULL;if (cur==NULL) {fprintf(stderr,"There are no nodes in the BSTree!!!");return ;}//若删除的是根节点,不会进入这个循环因为cur->data==ewhile (cur != NULL &&cur->data!=e) {pre=cur;if (e<cur->data) {cur=cur->left;} else if (e>cur->data) {cur=cur->right;}}if (cur == NULL) {printf("No %d element!\n", e);return;}//处理不同度数的节点BSNode *tmp=NULL;if (cur->left==NULL) {tmp=cur->right; //度为0或1}else if (cur->right==NULL) {tmp=cur->right; //度为1}else {deleteMiniNode(cur);//度为2的节点单独处理--tree->count;return;}//pre里面处理的是删除的度为0或1的节点if (pre) {//删除的元素不是根节点,pre!=NULL;if (e<pre->data) {//连在左边pre->left=tmp;}else if (e>pre->data) {//连在右边pre->right=tmp;}//删除的元素是根节点,pre==NULL;}else {tree->root=tmp;}free(cur);--tree->count;
#endif
}我们主要看这里:
//处理不同度数的节点BSNode *tmp=NULL;if (cur->left==NULL) {tmp=cur->right; //度为0或1}else if (cur->right==NULL) {tmp=cur->right; //度为1}else {deleteMiniNode(cur);//度为2的节点单独处理--tree->count;return;}//处理的是删除的度为0或1的节点if (pre) {//删除的元素不是根节点,pre!=NULL;if (e<pre->data) {//连在左边pre->left=tmp;}else if (e>pre->data) {//连在右边pre->right=tmp;}//删除的元素是根节点,pre==NULL;且根只有左子树或右子树}else {tree->root=tmp;}free(cur);--tree->count;
先分别处理要删除的节点的度数为0,1,2的情况应该把要删除节点的哪一边交给pre,并单独处理度数为2的节点,再开始处理pre和tmp的连接关系逻辑,即删除的度数为0或1的节点在pre的左边还是右边,特别注意当我们删除的节点为根节点(此时的根节点只有左子树或右子树,因为如果根节点有左右子树会走static void deleteMiniNode(BSNode *node);这个逻辑)时不会进入循环,因为cur->data==e,所以pre等于NULL,此时应该tree->root=tmp;这种情况必须单独处理,因为根节点没有父节点,删除后需要直接更新树的根指针(tree->root),而不是像普通节点那样更新父节点的 left 或 right 指针。
最后来测一下:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "binarySearchTree.h"
void test03() {int data[] = {55, 33, 100, 22, 80, 45, 130, 8, 120, 121, 122};BSTree *tree = createBSTree("stu01");if (tree == NULL) {return;}for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {insertBSTree(tree, data[i]);}printf("tree height: %d\n", heightBSTree(tree));printf("inOrder traversal:\n");inOrderBSTree(tree);printf("\n");deleteBSTree(tree, 55);inOrderBSTree(tree);printf("tree root: %d\n", tree->root->data);releaseBSTree(tree);
}int main() {//test01();//test02();test03();return 0;
}
结果:
D:\work\DataStruct\cmake-build-debug\02_TreeStruct\BSTree.exe
tree height: 6
inOrder traversal:
[stu01]Tree: 8 22 33 45 55 80 100 120 121 122 130[stu01]Tree: 8 22 33 45 80 100 120 121 122 130
tree root: 80
There are 0 nodes.进程已结束,退出代码为 0今天写的比较多好好消化,大概先写这些吧,今天的博客就先写到这,谢谢您的观看。
