算法题（181）：最大直方矩形面积

审题：

本题需要我们找到以一条任意高度水平线分割的图形中矩形的最大面积，其中该矩形中间不能有空位

思路：

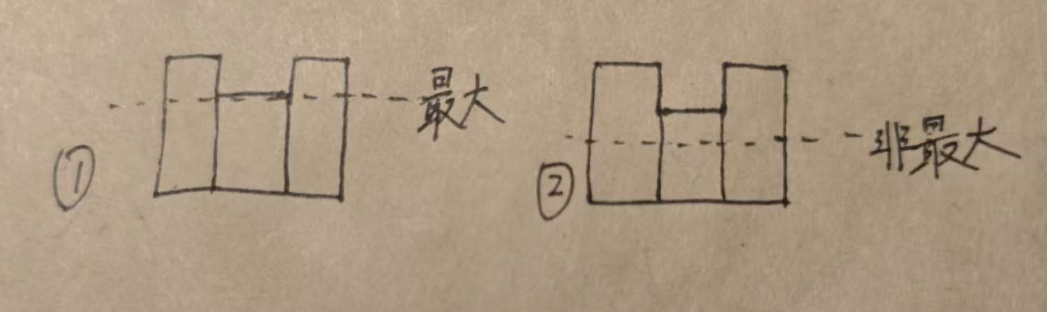
我们先思考一下最终矩形的构成情况，最终矩形的高度一定是等于其中一个竖矩形的最大高度的，因为若低于那个竖矩形则一定会有一个更大矩形，此时结论会矛盾

图解：

所以最终矩形一定是以从某一个竖矩形向两侧延伸得来，故问题变成了如何求出某个高度的矩形的左右边界（比他高度低的最近位置），此时就可以使用单调栈了
方法一：单调栈

第一步：录入数据

第二步：利用单调栈查找左侧和右侧的边界

第三步：根据前面得到的矩形左右边界和矩形高度计算出矩形的面积，并比较出max面积

解题：

#include<iostream>
#include<stack>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
ll n;
ll v[N];
ll l[N], r[N];
int main()
{while (cin >> n, n){for (int i = 1; i <= n; i++) cin >> v[i];//查找左侧边界stack<int> s;for (int i = 1; i <= n; i++){while (s.size() && v[s.top()] >= v[i]) s.pop();if (s.size()) l[i] = s.top();else l[i] = 0;s.push(i);}//清除单调栈数据残留while (s.size()) s.pop();//查找右侧边界for (int i = n; i >= 1; i--){while (s.size() && v[s.top()] >= v[i]) s.pop();if (s.size()) r[i] = s.top();else r[i] = n+1;s.push(i);}//比对出最终答案ll ret = 0;for (int i = 1; i <= n; i++){ret = max(ret, v[i] * (r[i] - l[i] - 1));}cout << ret << endl;}return 0;
}

SP1805 HISTOGRA - Largest Rectangle in a Histogram - 洛谷