Gumbel-Softmax函数
Gumbel-Softmax函数
背景动机
在许多任务中,我们需要从一个离散分布中采样,例如从one-hot编码中选出某个类别:
- 但是离散采样操作是不可导的,这使得无法通过反向传播更新参数
- Gumbel-Softmax提供了一种近似采样的方法,它是可微的,因此可以端到端训练神经网络
什么任务需要离散分布采样
- 神经架构搜索:在给定多个可能的网络组件中选择一个子结构
- 强化学习:代理在每一步需要从有限的动作空间中选择一个动作,如走上/下/走/右
Gumbel-Max Trick
如果我们希望从一个离散的概率分布z=[z1,z2....,zK]z=[z_1,z_2....,z_K]z=[z1,z2....,zK]中采样一个类别,可以通过以下方式实现:
y=argmax[log(zi)+gi]
y = argmax[log(z_i)+g_i]
y=argmax[log(zi)+gi]
其中gi=Gumbel(0,1)g_i=Gumbel(0,1)gi=Gumbel(0,1),这个过程称为Gumbel-Max trick,可以视为在logits上加上噪声后取最大值。
然而,argmax操作显然不可导
为了使Gumbel-Max变为可导,我们将argmax用softmax来近似
yi=exp((log(zi)+gi)/τ)∑j=1Kexp((log(zi)+gi)/τ)
y_i = \frac{exp((log(z_i)+g_i)/\tau)}{\sum_{j=1}^Kexp((log(z_i)+g_i)/\tau)}
yi=∑j=1Kexp((log(zi)+gi)/τ)exp((log(zi)+gi)/τ)
- gi=Gumbel(0,1)是Gumbel噪声g_i = Gumbel(0,1)是Gumbel噪声gi=Gumbel(0,1)是Gumbel噪声
- τ>0\tau>0τ>0是温度参数
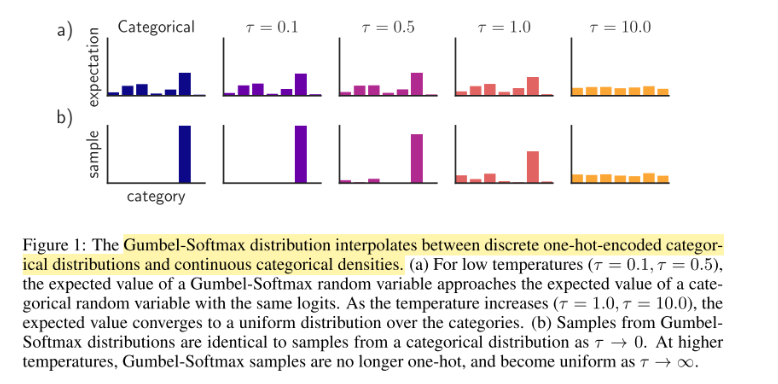
当τ→∞\tau\rightarrow\inftyτ→∞, Gumbel-Softmax输出趋近于平均分布(更平滑)
当τ→0\tau\rightarrow0τ→0,输出趋近于one-hot(更像真实采样,但梯度不稳定)
因此,训练时通常采用:高温度开始,逐渐降低温度
为什么说Gumbel-Softmax模拟了采样行为?
从一个离散概率分布z=[0.1,0.7,0.2]z=[0.1,0.7,0.2]z=[0.1,0.7,0.2]中采样,指的是:根据概率值,随机选择一个类别(one-hot)作为结果。
有70%概率选择第2类: [0,1,0]
有10%概率选择第1类:[1,0,0]
但是采样过程不可导。
Gumbel-Max Trick = 真实采样
y=argmax[log(zi)+gi]
y = argmax[log(z_i)+g_i]
y=argmax[log(zi)+gi]
举个例子:
- logits = [2.0, 1.0, 0.1]
Softmax 后输出:
[0.57, 0.31, 0.12] # 每次都一样,不是真采样
- Gumbel-Softmax(多次运行)
每次加上 Gumbel 噪声再 softmax,例如:
Sample 1: [0.97, 0.02, 0.01]
Sample 2: [0.03, 0.91, 0.06]
Sample 3: [0.05, 0.10, 0.85]
这些近似 one-hot 输出,就模拟了多次“真实采样”的过程。
为什么要使用log函数?
压缩大值,使噪声占比大
Gumbel 分布 (耿贝尔分布)
Gumbel 分布是一种极值分布,用于建模“最大值”的概率分布。
📌 标准 Gumbel(0,1) 分布的定义:
一个随机变量 g 服从标准 Gumbel 分布,当其概率密度函数(PDF)为:
f(g)=exp(−(g+e−g))
f(g) = exp(-(g+e^{-g}))
f(g)=exp(−(g+e−g))
如何采样Gumbel噪声
g=−log(−log(U))
g = - log(-log(U))
g=−log(−log(U))
def sample_gumbel(shape, eps=1e-20):U = torch.rand(shape)return -torch.log(-torch.log(U + eps) + eps)总结:Gumbel-Softmax在Softmax的基础上增加了噪声扰动性,从而达到离散分布采样的作用
