当前位置：首页 > news >正文

图像轮廓与凸包

news 2025/7/29 11:44:02

绘制轮廓

轮廓的含义

寻找轮廓

凸包特征检测

穷举法

QuickHull法

绘制凸包

图像轮廓特征查找

外接矩形

最小外接矩形

最小外接圆

总结

绘制轮廓

轮廓的含义

轮廓是一系列相连的点组成的曲线，代表了物体的基本外形。相对于边缘，轮廓是连续的，边缘不一定连续，如下图所示。轮廓是一个闭合的、封闭的形状。

轮廓的作用：形状分析，目标识别，图像分割

寻找轮廓

在绘制轮廓之前需要先找到相应的轮廓，在OpenCV中，使用cv2.findContours()来进行寻找轮廓，其原理过于复杂，这里只进行一个简单的介绍，具体的实现原理可参考：

https://zhuanlan.zhihu.com/p/107257870

寻找轮廓需要将图像做一个二值化处理，并且根据图像的不同选择不同的二值化方法来将图像中要绘制轮廓的部分置为白色，其余部分置为黑色。也就是说，我们需要对原始的图像进行灰度化、二值化的处理，令目标区域显示为白色，其他区域显示为黑色，如下图所示。

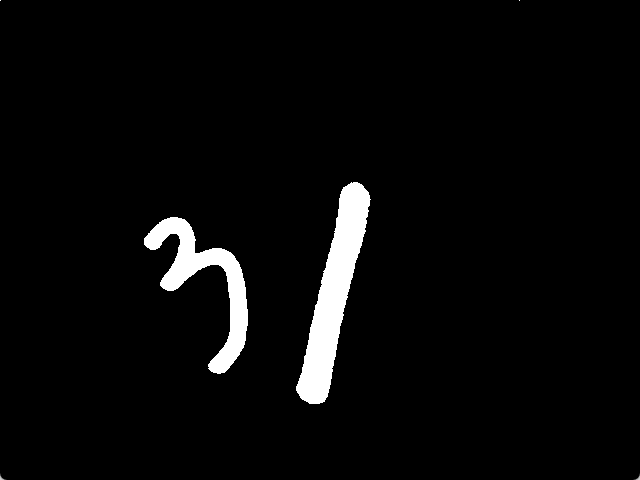
后，对图像中的像素进行遍历，当一个白色像素相邻（上下左右及两条对角线）位置有黑色像素存在或者一个黑色像素相邻（上下左右及两条对角线）位置有白色像素存在时，那么该像素点就会被认定为边界像素点，轮廓就是有无数个这样的边界点组成的。

下面具体介绍一下cv2.findContours()函数，其函数原型为：

contours,hierarchy = cv2.findContours(image，mode，method)

返回值为轮廓点坐标和层级关系；

countours表示获取到的轮廓点的列表，有多少轮廓就有多少子列表，每一个子列表都表示了一个轮廓中所以点的坐标；

hierarchy表示轮廓之间的关系；

image表示输入的额二值化图像；

mode表示轮廓的检索模式，mode参数共有四个选项分别为：RETR_LIST，RETR_EXTERNAL，RETR_CCOMP，RETR_TREE。

method为轮廓的表示方法，method参数有三个选项：CHAIN_APPROX_NONE、CHAIN_APPROX_SIMPLE(只存储有用的点)、CHAIN_APPROX_TC89_L1。

凸包特征检测

穷举法

将集中的点进行两两配对，并进行连线，对于每条直线，检查其余所有的点是否处于该直线的同一侧，如果是，那么说明构成该直线的两个点就是凸包点，其余的线依次进行计算，从而获取所有的凸包点。

缺点：时间复杂度高，不断使用for循环，耗时。

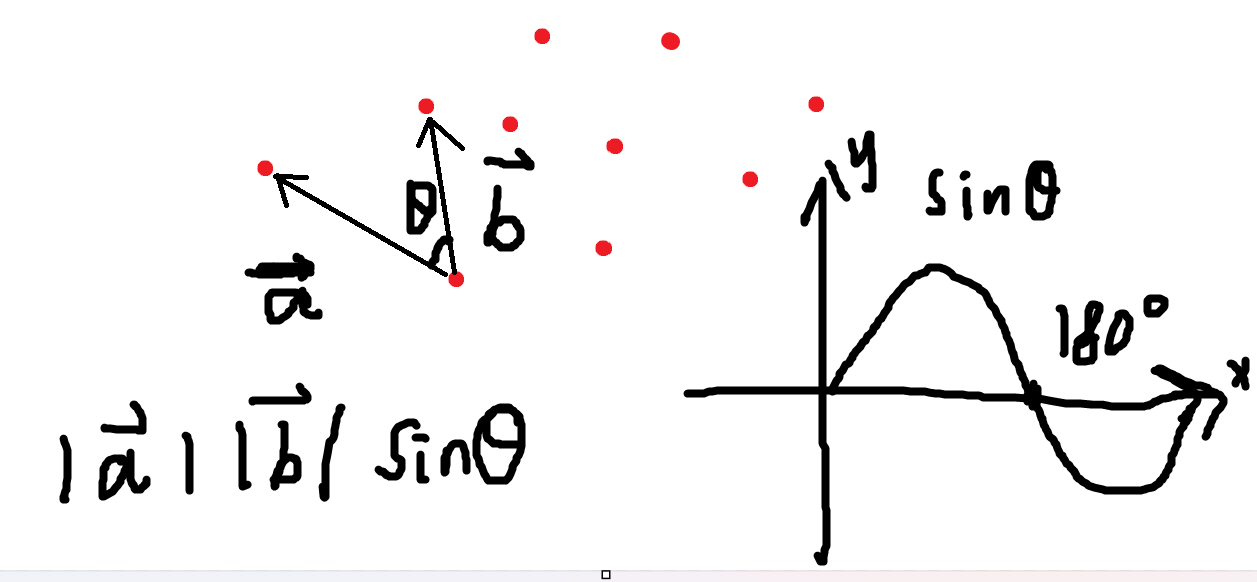
QuickHull法

将所有点放在二维坐标系中，找到横坐标最小和最大的两个点P_1和P_2并连线。此时整个点集被分为两部分，直线上为上包，直线下为下包。然后找到上包中的点距离该直线最远的点P_3,连线并寻找直线P1P3左侧的点和P2P3右侧的点，然后重复本步骤，直到找不到为止。对下包也是这样操作。

绘制凸包

在绘制凸包点之前需要先获取凸包点，获取凸包点在OpenCV中通过API

cv2.convexHull(points) 来实现的

point当中输入参数为图像的轮廓

hull = cv2.convexHull(counters[0])，获取第一个轮廓的凸包点，若要获取多个轮廓的凸包点可进行for循环遍历。

绘制凸包在OpenCV中通过cv2.polylines(image, pts, isClosed, color, thickness=1) 实现

image：要绘制线条的目标图像，它应该是一个OpenCV格式的二维图像数组（如numpy数组）。

pts：一个二维 numpy 数组，每个元素是一维数组，代表一个多边形的一系列顶点坐标。

isClosed：布尔值,表示是否闭合多边形,如果为 True，会在最后一个顶点和第一个顶点间自动添加一条线段，形成封闭的多边形。

color：线条颜色，可以是一个三元组或四元组，分别对应BGR或BGRA通道的颜色值，或者是灰度图像的一个整数值。

thickness（可选）：线条宽度，默认值为1。

图像轮廓特征查找

外接矩形

形状的外接矩形有两种，如下图，绿色的叫外接矩形，表示不考虑旋转并且能包含整个轮廓的矩形。其中，外接矩形可根据获得到的轮廓坐标中最上、最下、最左、最右的点的坐标来绘制外接矩形，也就是下图中的绿色矩形。

 # 绘制外接矩形circumscribed_contour_image = contour_image.copy()for cnt in contours:x, y, w, h = cv2.boundingRect(cnt)cv2.rectangle(circumscribed_contour_image, (x, y), (x + w, y + h), (0, 0, 255), 2)

最小外接矩形

最小外接矩形就是上图所示的蓝色矩形，寻找最小外接矩形使用的算法叫做旋转卡壳法。下面简单说明一下旋转卡壳法的思路：

我们了解到了凸包的概念，凸包就是一个点集的凸多边形，它是这个点集所有点的凸壳，点集中所有的点都处于凸包里，构成凸包的点我们叫做凸包点。而旋转卡壳法就是基于凸包点进行的，

旋转卡壳法有一个很重要的前提条件：对于多边形P的一个外接矩形存在一条边与原多边形的边共线。

假设某凸包图如下所示：

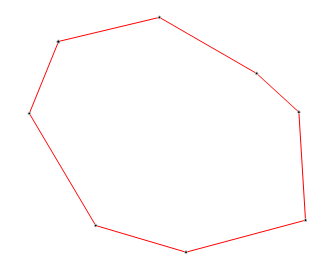
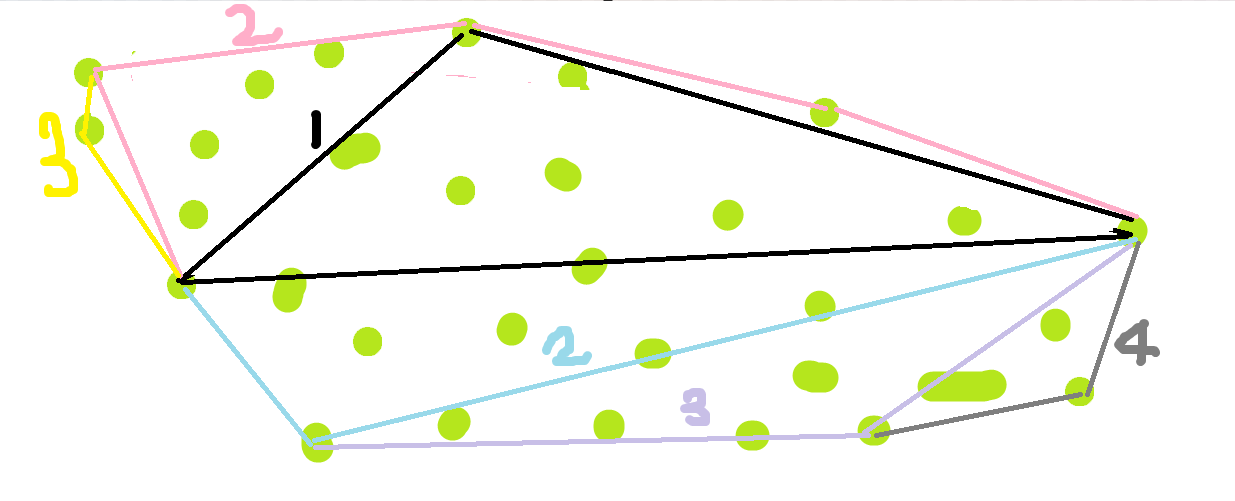
根据前提条件，上面的凸多边形的最小外接矩形与凸多边形的某条边是共线的。因此我们只需要以其中的一条边为起始边，然后按照逆时针方向计算每个凸包点与起始边的距离，并将距离最大的点记录下来。

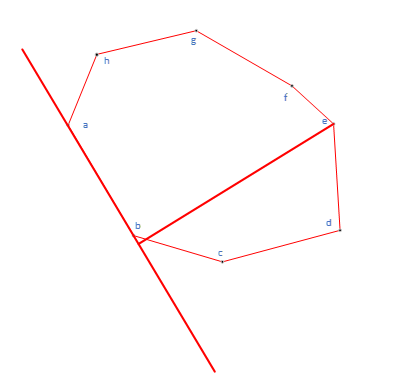
如上图所示，我们首先以a、b两点为起始边，并计算出e点离起始边最远，那么e到起始边的距离就是一个矩形的高度，因此我们只需要再找出矩形的宽度即可。对于矩形的最右边，以向量 $\overline{{a b}}$ 为基准，然后分别计算凸包点在向量 $\overline{{a b}}$ 上的投影的长度，投影最长的凸包点所在的垂直于起始边的直线就是矩形最右边所在的直线。

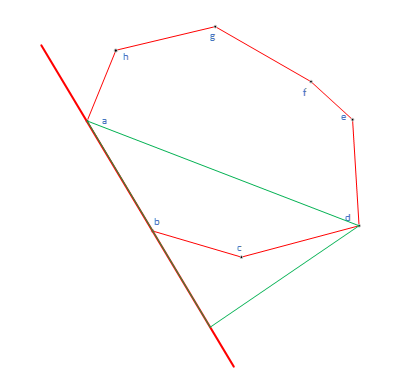
如上图所示，d点就是在向量 $\overline{{a b}}$ 上投影最长的凸包点，那么通过d点垂直于直线ab的直线就是矩形的右边界所在的直线。矩形的左边界的也是这么计算的，不同的是使用的向量不是 $\overline{{a b}}$ 而是 $\overline{{b a}}$ 。

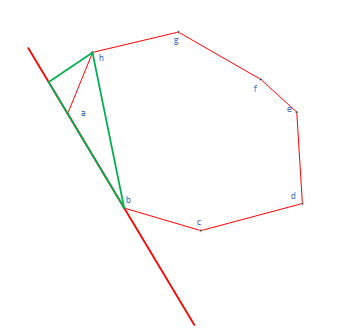
如上图所示，h点垂直于ab的直线就是以ab为起始边所计算出来的矩形所在的左边界所在的直线。其中矩形的高就是e点到直线ab的距离，矩形的宽是h点在向量上 $\overline{{b a}}$ 的投影加上d点在向量 $\overline{{a b}}$ 上的投影减去ab的长度，即：
$w i d t h=|\overline{{{b h}}}|\times\cos a+|\overline{{{a d}}}|\times\cos\theta-|\overline{{{a b}}}|$

于是我们就有了以ab为起始边所构成的外接矩形的宽和高，这样就可以得到该矩形的面积。然后再以bc为起始边，并计算其外接矩形的面积。也就是说凸多边形有几个边，就要构建几次外接矩形，然后找到其中面积最小的矩形作为该凸多边形的最小外接矩形。

OpenCV中实现的API为rect = cv2.minAreaRect(cnt)

传入的cnt参数为contours中的轮廓,可以遍历contours中的所有轮廓,然后计算出每个轮廓的小面积外接矩形

rect 是计算轮廓最小面积外接矩形:rect 结构通常包含中心点坐标 (x, y)、宽度 width、高度 height 和旋转角度 angle

cv2.boxPoints(rect).astype(int)

cv2.boxPoints(rect)返回是一个形状为 4行2列的数组，每一行代表一个点的坐标（x, y），顺序按照逆时针或顺时针方向排列

将最小外接矩形转换为边界框的四个角点，并转换为整数坐标

最后再通过绘制轮廓显示最小外接矩形

最小外接圆

寻找最小外接圆使用的算法是Welzl算法。Welzl算法基于一个定理：希尔伯特圆定理表明，对于平面上的任意三个不在同一直线上的点，存在一个唯一的圆同时通过这三个点，且该圆是最小面积的圆（即包含这三个点的圆中半径最小的圆，也称为最小覆盖圆）。进一步推广到任意 n 个不在同一圆上的点，总存在一个唯一的最小覆盖圆包含这 n 个点。

在OpenCV中，可以直接使用cv2.minEnclosingCircle()来获取最小外接圆，该函数只需要输入一个参数，就是要绘制最小外接圆的点集的坐标，然后会返回最小外接圆的圆心坐标与半径。通过该函数返回的内容信息即可绘制某点集的最小外接圆。如下图所示：