哈夫曼树的解析

权 (weight)：将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度： 从根结点到该结点之间的路径长度与该结点的权的乘积。

树的带权路径长度：树中所有叶子结点的带权路径长度之和。 记作： \(\boldsymbol{WPL = \sum_{k = 1}^{n} w_k l_k}\) ，其中 \(w_k\) 为权值，\(l_k\) 为结点到根的路径长度

引入哈夫曼树，有一个关键，是把出现次数越多的，放在离根越近的地方，这样可以节省时间

树的路径长度：根到每个结点的路径之和

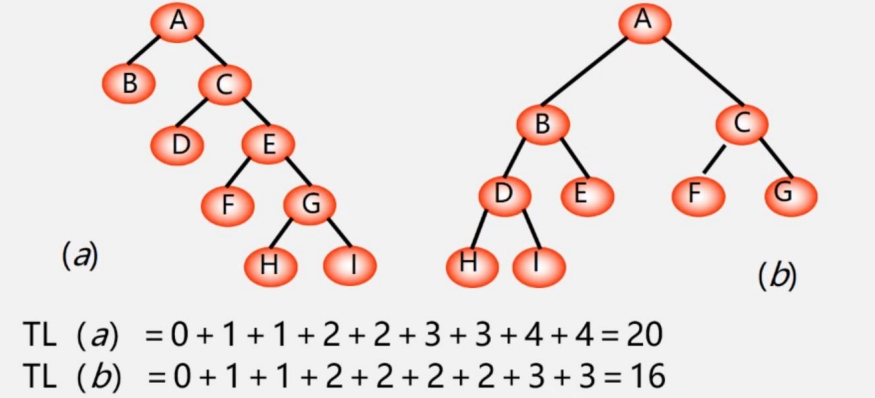
分析（a），A到A的路径为0，A到B为1，A到C为1，A到D为2（A-->C-->D)，以此类推

我们不难发现b的路径长度比a短，说明效率更高，b是完全二叉树（完全二叉树，指的除了叶子结点这一排，其他结点均满，并且最后一排的叶子结点必须从左往右顺序摆放）

由此我们得出结论：结点相同的二叉树中，完全二叉树的路径最短

哈夫曼树的相关定义：

权 (weight)：将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度： 从根结点到该结点之间的路径长度与该结点的权的乘积。

树的带权路径长度：树中所有叶子结点的带权路径长度之和。 WPL=∑Wk*Lk（k从1到n）

举个例子帮助我们理解：

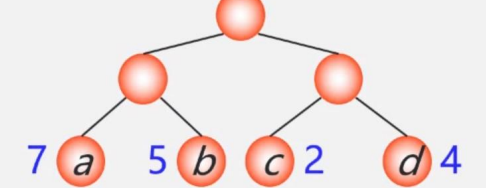
a、b、c、d的路径长度分别是：2、2、2、2

所以结点的带权路径长度=7*2+5*2+2*2+4*2=36

哈夫曼树：最优树（最优树的比较是在树的度相同的情况下）

“度” 就是指一个结点拥有的子结点（子树）数量，比如根A带了BC两个子树，A的度为2，叶子结点度为0

哈夫曼树：最优二叉树（带权路径长度也就是WPL最短的二叉树）

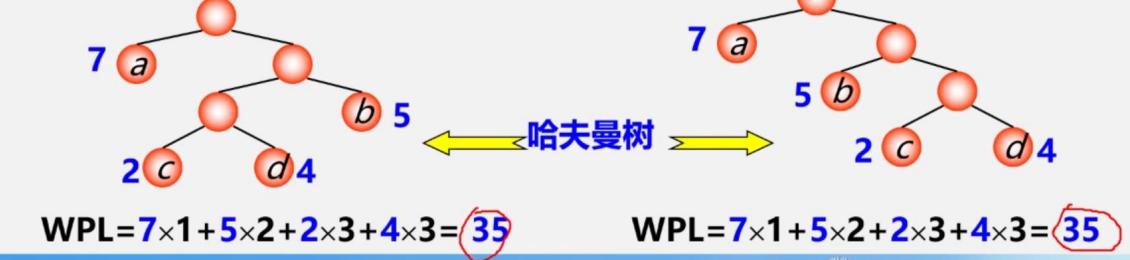
上图表明，结点相同的哈夫曼树，是不唯一的

满二叉树不一定是哈夫曼树

哈夫曼树中权越大的叶子离根越近

具有相同带权结点的哈夫曼树不惟一

如何构造哈夫曼树？

简要说明：我们找出两个权最小的，连在一起，然后再继续比较，找出两个最小的，我们直接用一个例子来说明

我们知道，目前最小的两个权值是2-c，4-d，这两个 结点构成一个小树

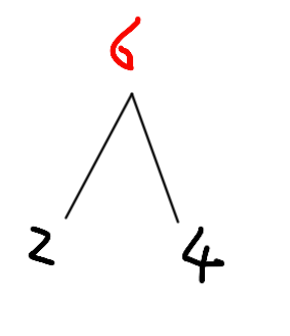
然后6再与，7和5比较，最小的是6和5

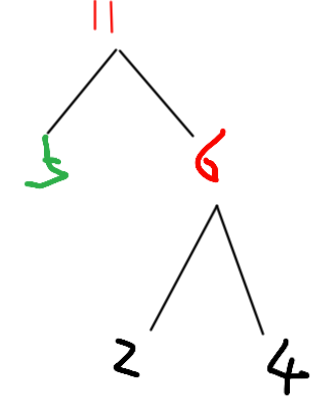
最后剩11和7，再拼成一棵树即可

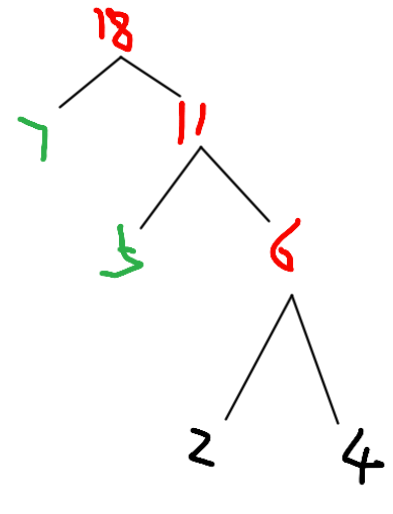
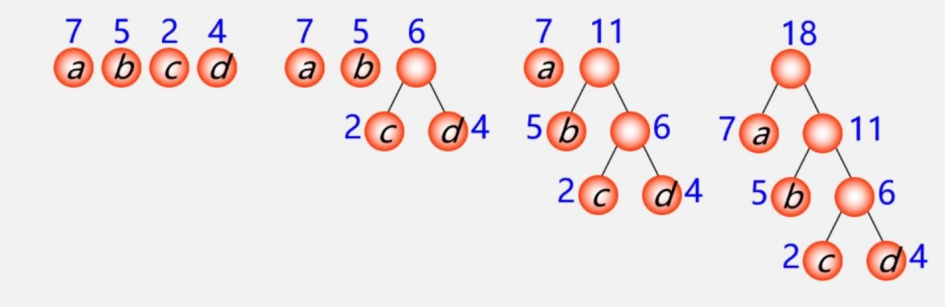
总结：

1、在哈夫曼算法中，初始时有n棵二叉树，要经过n-1次合并最终形成哈夫曼树。

2、经过n-1次合并产生n-1个新结点，且这n-1个新结点都是具有两个孩子的分支结点。

可见：哈夫曼树中共有n + n-1 = 2n-1个结点，且其所有的分支结点的度均不为1（0或2）。

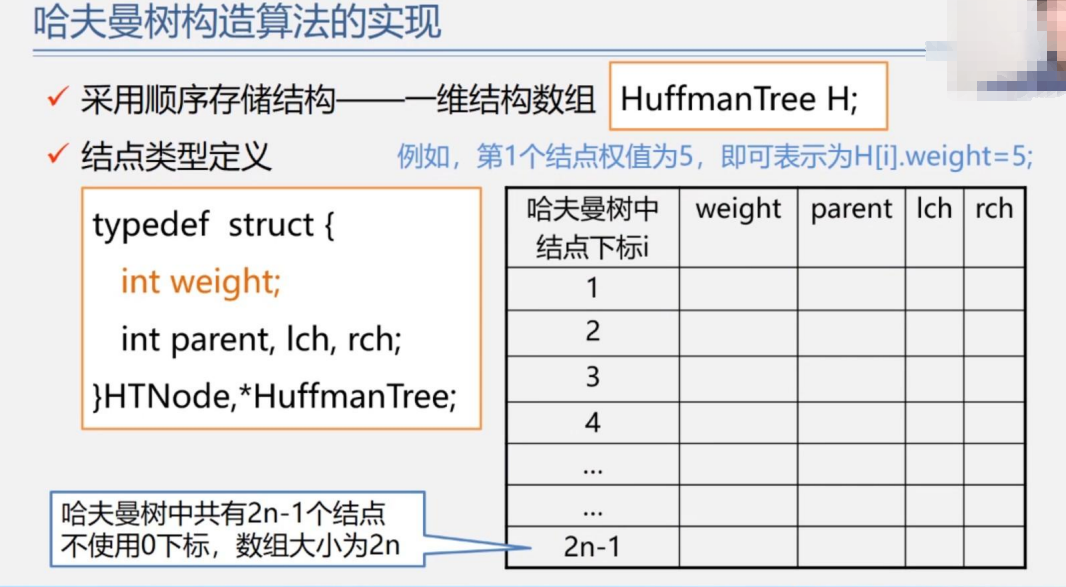
我们举个例子帮助理解：

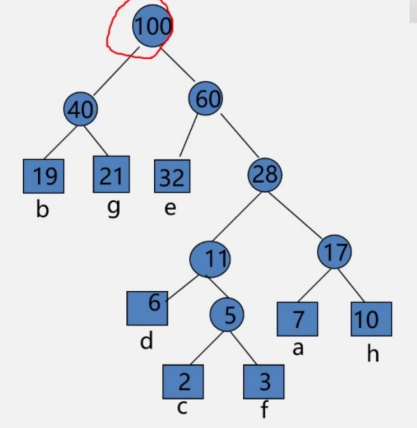
例，有 n=8，权值为 W={7，19，2，6，32，3，21，10} 构造哈夫曼树

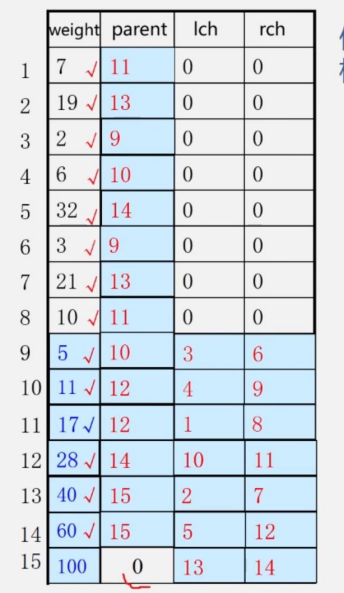
先找出最小的两个构成树，是2和3，他们的双亲是5，在下标为9的数组里存储

再看11，双亲是28，在下标为12的地方存储，而左孩6和右孩5分别在4和9存储

哈夫曼编码：

结点的左分支为0，右分支为1

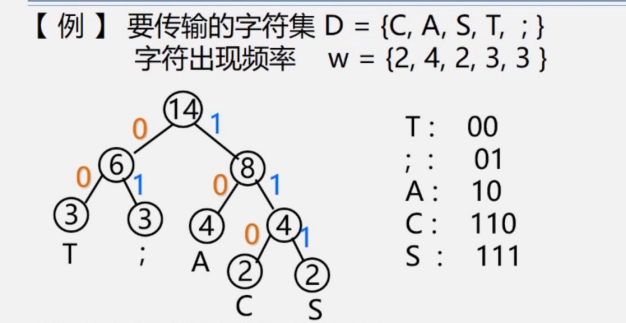
我们构造出哈夫曼树以后，分别对左分支编号均为0，右分支编号均为1，图已经很明显的能看出这个编码的原理

我们再详细解释一下吧，首先构造哈夫曼树，C和S对应的权最小，先构成一个小树4，以此类推，构成哈夫曼树，然后依次编号后，从上至下读取，比如T，是14->6->3这条路径，也就是00

再举一个例子：

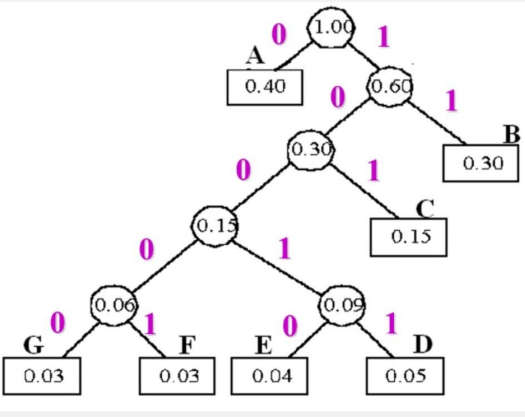
我们可以直接从图中知道各个结点的编码

哈夫曼编码的算法实现，用上边这个例子，我们来进一步了解一下原理

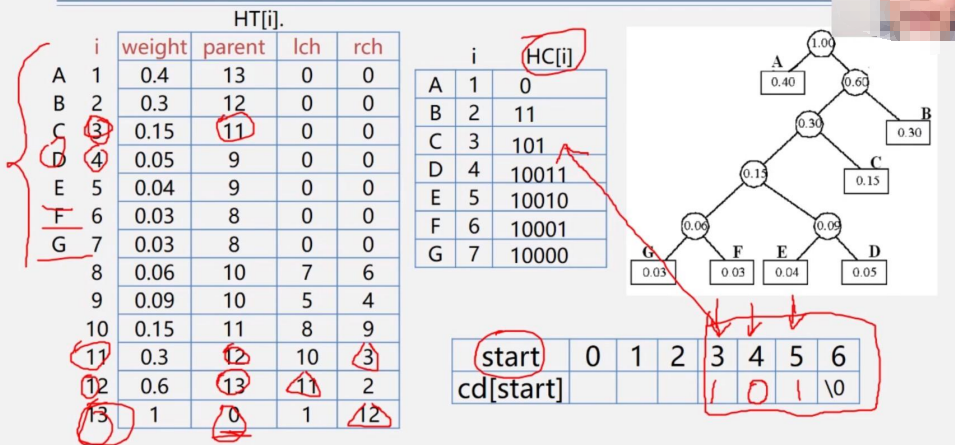
我们用一个一维数组来记录，依次从右往左记录，读取的时候是从左往右读取，举个例子，我们看一下C的编码

C在下标为3的位置里，双亲在下标为11的数组，我们发现，3就存在下标为11的右分支里，记为1，一维数组中下标为5的位置，我们填上1

继续在下标为11的数组里分析，他的双亲是12，我们来到12号，发现11在12的做分支，我们记为0，录入一维数组下标为4的窗口

接着，继续分析，下标为12的数组中，双亲是13，我们来到下标为13的位置，发现12是13的右分支，记为1，录入一维数组下标为3的窗口，到此结束，所以从左往右读，C的编码是101