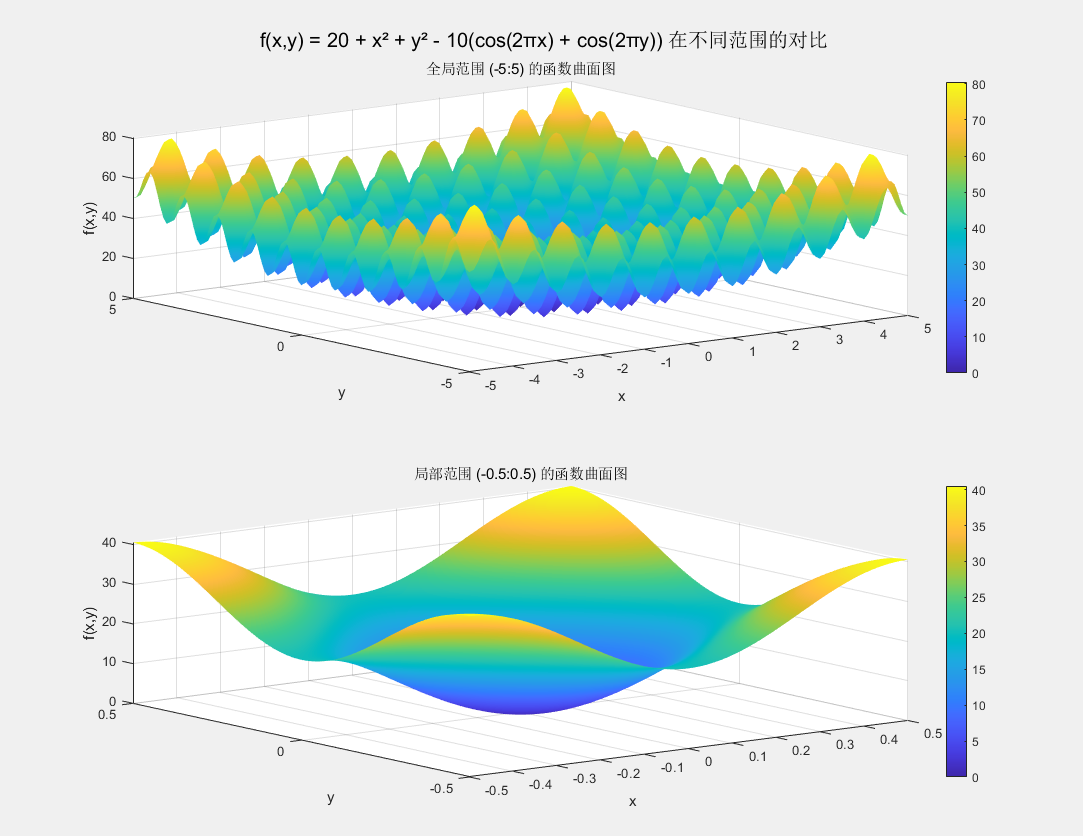
Rastrigin函数简介

前言

提醒：
文章内容为方便作者自己后日复习与查阅而进行的书写与发布，其中引用内容都会使用链接表明出处（如有侵权问题，请及时联系）。
其中内容多为一次书写，缺少检查与订正，如有问题或其他拓展及意见建议，欢迎评论区讨论交流。

内容由AI辅助生成，仅经笔者审核整理，请甄别食用。

---

Rastrigin函数是在优化领域中非常经典的一个测试函数，常被用于评估优化算法的性能，如遗传算法、粒子群优化算法等。以下是关于它的详细介绍：

1. 函数定义

Rastrigin函数是一个多变量函数，其一般形式为：
$$f(\mathbf{x})=A\cdot n+\sum _{i=1}^n\left[x_i^2-A\cdot \cos (2\pi x_i)\right]$$
其中：

• $\mathbf{x}=[x_1,x_2,\cdots ,x_n]$是一个 $n$ 维的向量，表示函数的输入变量，也就是优化问题中的决策变量。
• $n$是变量的维度，即向量 $\mathbf{x}$ 的长度，代表优化问题的自由度，比如在二维空间中 $n=2$，三维空间中 $n=3$ 等。
• $A$是一个常数，通常取 $A=10$，用于调整函数的形态和复杂度。

当 $A=10$ 时，函数形式变为：
$$f(\mathbf{x})=10\cdot n+\sum _{i=1}^n\left[x_i^2-10\cdot \cos (2\pi x_i)\right]$$

2. 函数特性

• 全局最小值：函数的全局最小值为 $f({\mathbf{x}}^{\ast })=0$，当且仅当 $x_1=x_2=\cdots =x_n=0$ 时取得。这是我们使用各种优化算法试图找到的目标值。
• 多模态性：Rastrigin函数是一个典型的多模态函数，在其定义域内存在大量的局部最小值。以二维情况为例，它的函数图像看起来像一个布满小坑的地形，每个小坑都对应一个局部最小值。 数学上，对函数求偏导数可以找到局部极值点。对于 $f(\mathbf{x})$ 中的第 $i$ 个变量 $x_i$ 求偏导数：
  $$\frac{\partial f}{\partial x_i}=2x_i+20\pi \sin (2\pi x_i)$$
  令偏导数等于0，即 $2x_i+20\pi \sin (2\pi x_i)=0$，解这个方程可以得到局部极值点的 $x_i$ 坐标。但由于正弦函数的周期性和非线性，方程有多个解，也就意味着存在多个局部最小值。
• 周期性：函数中的 $\cos (2\pi x_i)$ 项具有周期性，周期为 $T=1$。这使得函数在不同的周期内呈现相似的形态，增加了优化的难度，因为优化算法可能会在不同周期内找到相似的局部最小值，而难以跳出局部最优去寻找全局最优。
• 可扩展性：该函数可以很方便地扩展到更高维度，随着维度 $n$ 的增加，局部最小值的数量会呈指数增长，优化问题的难度也会急剧上升。

3. 常见定义域

在实际应用中，Rastrigin函数通常在一个有限的定义域内进行优化。常见的定义域设置为：
$$x_i\in [-5.12,5.12],i=1,2,\cdots ,n$$
这个定义域是为了在一个合理的范围内评估优化算法的性能，避免因定义域过大或过小对算法效果产生不合理的影响。

4. 应用场景

• 优化算法测试：由于Rastrigin函数具有多模态、复杂的局部最小值分布等特性，是测试和比较各种优化算法性能的理想选择。通过在该函数上运行优化算法，可以评估算法的全局搜索能力、收敛速度、避免陷入局部最优的能力等。
• 工程优化问题的近似模型：在一些复杂的工程优化场景中，如机械设计、电子电路设计等，目标函数可能非常复杂，难以直接求解。可以使用Rastrigin函数这样的测试函数来近似模拟目标函数的复杂特性，帮助研究人员开发和验证优化策略。

5. 可视化python代码（三维）

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import matplotlib# 强制使用Windows系统预装的中文字体
matplotlib.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]  # 优先使用黑体，其次微软雅黑
matplotlib.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题# 定义Rastrigin函数
def rastrigin(x):n = x.shape[0]return 10 * n + np.sum([xi**2 - 10 * np.cos(2 * np.pi * xi) for xi in x])# 生成数据
x = np.linspace(-5.12, 5.12, 100)
y = np.linspace(-5.12, 5.12, 100)
X, Y = np.meshgrid(x, y)
Z = np.zeros_like(X)
for i in range(X.shape[0]):for j in range(X.shape[1]):Z[i, j] = rastrigin(np.array([X[i, j], Y[i, j]]))# 绘图
fig = plt.figure(figsize=(12, 5))
ax1 = fig.add_subplot(121, projection='3d')
surf = ax1.plot_surface(X, Y, Z, cmap=cm.coolwarm, linewidth=0, antialiased=True)
ax1.set_title('Rastrigin函数3D曲面图')
ax1.set_xlabel('x1')
ax1.set_ylabel('x2')
ax1.set_zlabel('函数值')
fig.colorbar(surf, ax=ax1)ax2 = fig.add_subplot(122)
contour = ax2.contourf(X, Y, Z, levels=50, cmap=cm.coolwarm)
ax2.set_title('Rastrigin函数等高线图')
ax2.set_xlabel('x1')
ax2.set_ylabel('x2')
fig.colorbar(contour, ax=ax2)plt.tight_layout()
plt.show()

运行结果

matlab运行结果：

---