当前位置：首页 > news >正文

【CF】Day112——杂题 (逆向思维 | 二分 + 贪心 | 单调队列优化DP | 二进制 + 前缀和 | 二分图判断 | 暴力枚举)

news 2025/7/28 9:42:31

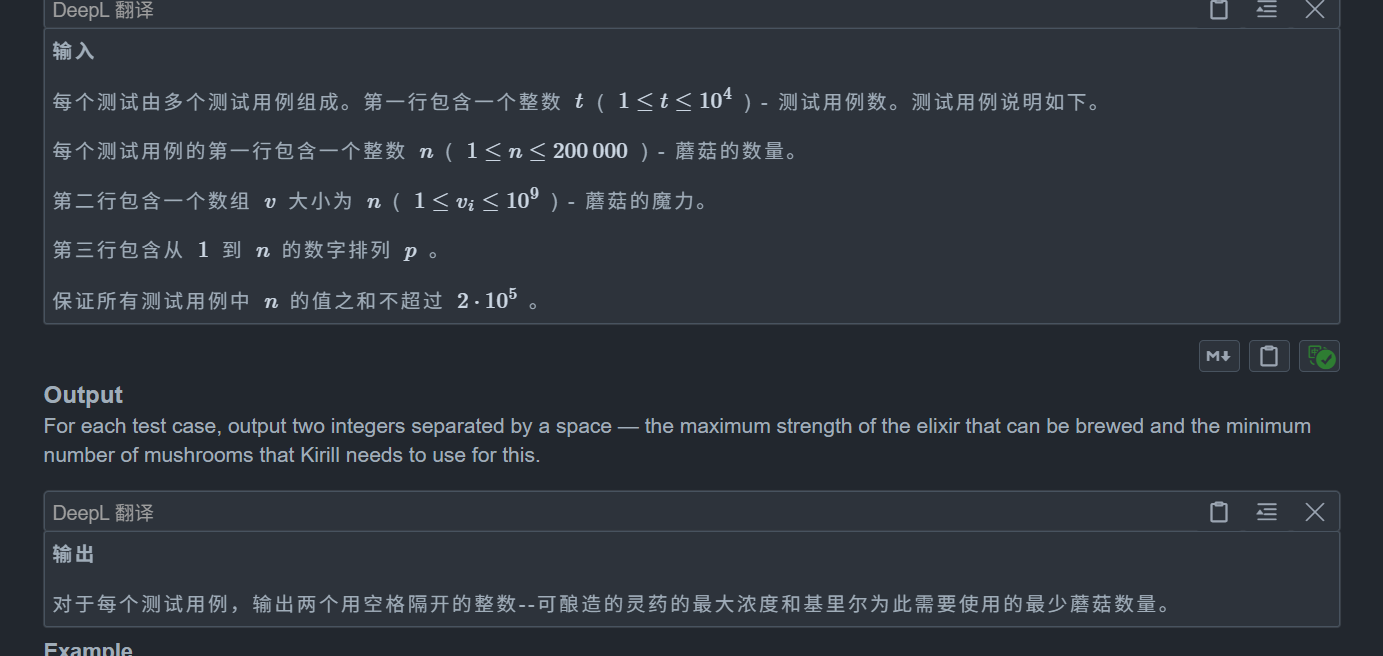
F. Kirill and Mushrooms

题目：

思路：

逆向思维

对于这种有删除操作的题目，其实我们不妨去往逆向的方向想，这是一种模板了

这题也是如此，我们不妨考虑一个一个加数字，然后全程维持最大值

具体的，我们利用一个优先队列来存储数值，如果当前队列大小大于我们能选的数，那么就把弹出堆顶（此处为小根堆），答案即为 size * top

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"
int n;
int v[200005];
int p[200005];
priority_queue<int,vector<int>,greater<>> pq;
void solve()
{cin >> n;for (int i = 1; i <= n; i++){cin >> v[i];}for (int i = 1; i <= n; i++){cin >> p[i];}int ans = 0, num = 0;//逆向思维，考虑一个一个放入数字，枚举选了 i 个数for (int i = n; i >= 0; i--){pq.push(v[p[i]]);while (pq.size() > i){pq.pop();}if(pq.size() >= i && pq.top() * i >= ans){ans = pq.top() * i;num = i;}}cout << ans << " " << num << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

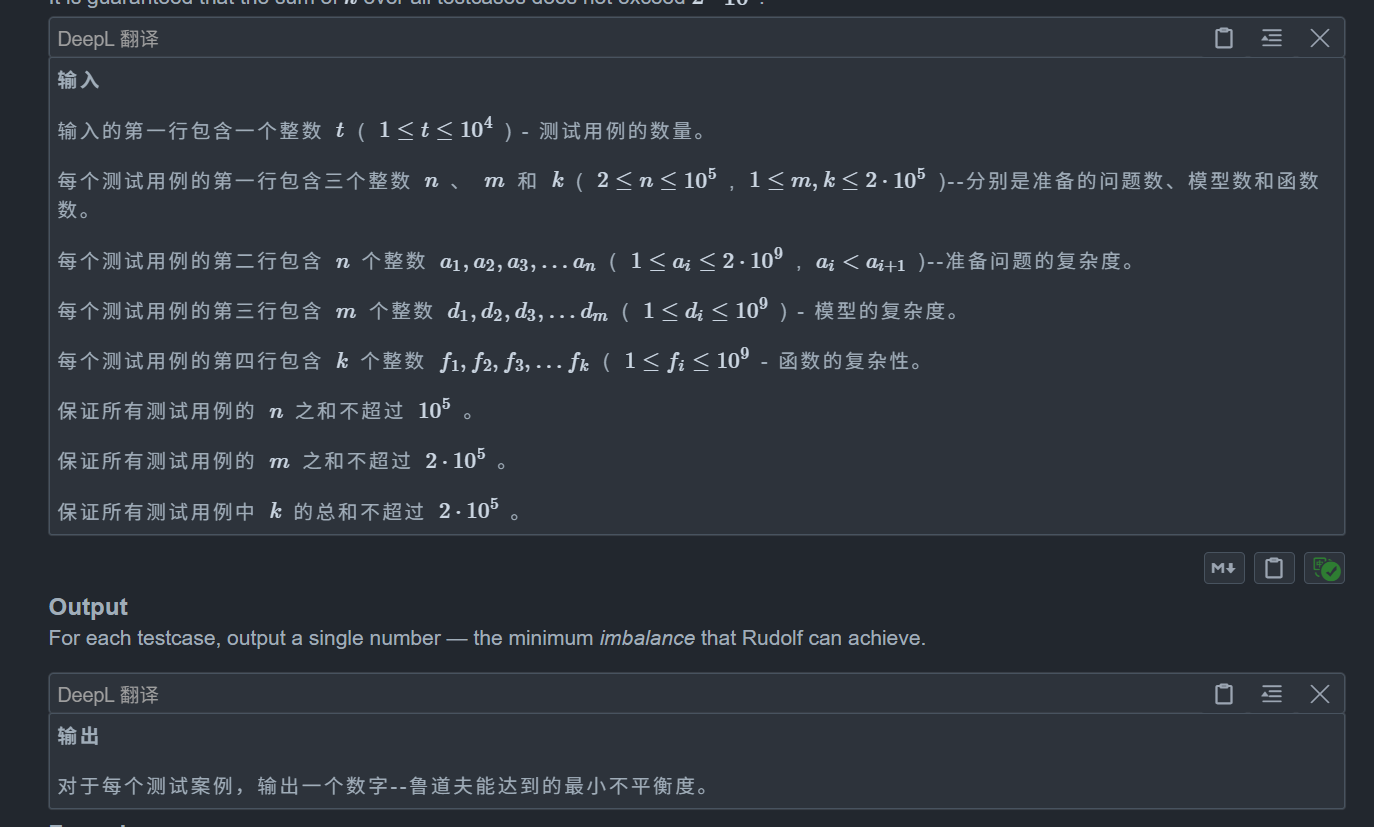
F. Rudolf and Imbalance

题目：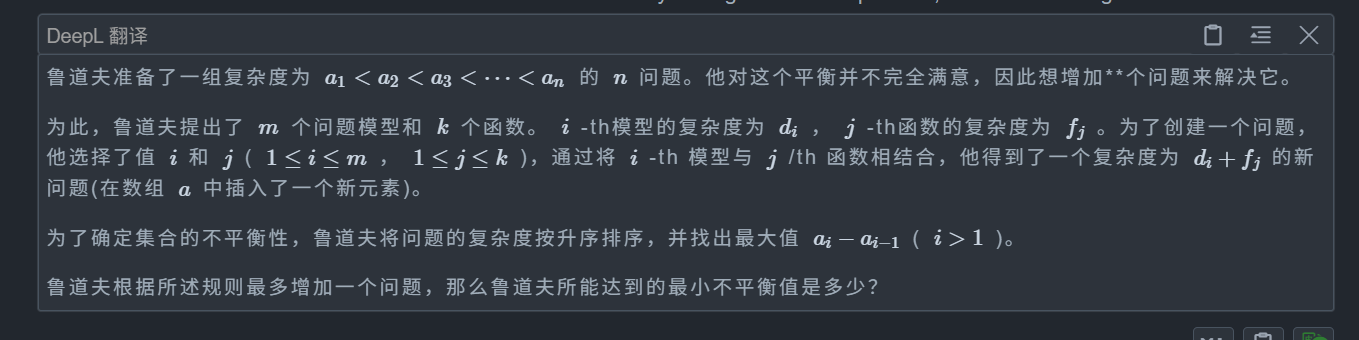

思路：

二分 + 贪心

本题的关键点在于明白我们最多只能改一个，那么我们只需要存储两个值，一个为最大值，一个为次大值，同时我们存储最大值对应的左边数和右边数

由于我们只能更改一个，那么显然是更改最大值更优，为了使得最大值变小，我们贪心的想肯定是最好分成平均数，所以我们枚举 d，去 f 中二分最接近 (l+r) / 2 的数，然后计算答案

特别的，由于我们还有一个次大值，所以还需比较，以及二分的结果不一定等于平均值，所以我们还要往后找一个再次比较

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"
int n, m, k;
int a[100005];void solve()
{cin >> n >> m >> k;set<int> d, f;int mx = -1, l = 0, r = 0, mx2 = -1;for (int i = 0; i < n; i++){cin >> a[i];if (i){int nx = a[i] - a[i - 1];if (nx > mx){mx2 = mx;mx = nx;l = a[i - 1], r = a[i];}else if (nx > mx2){mx2 = nx;}}}for (int i = 0; i < m; i++){int x;cin >> x;d.insert(x);}for (int i = 0; i < k; i++){int x;cin >> x;f.insert(x);}int ans = mx;for (auto &dx : d){auto it = f.lower_bound((l+r) / 2 - dx);int df = *it + dx;ans = min(ans, max(abs(r - df), abs(df - l)));if (it != f.begin()){it--;df = *it + dx;ans = min(ans, max(abs(r - df), abs(df - l)));}}cout << max(ans, mx2) << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

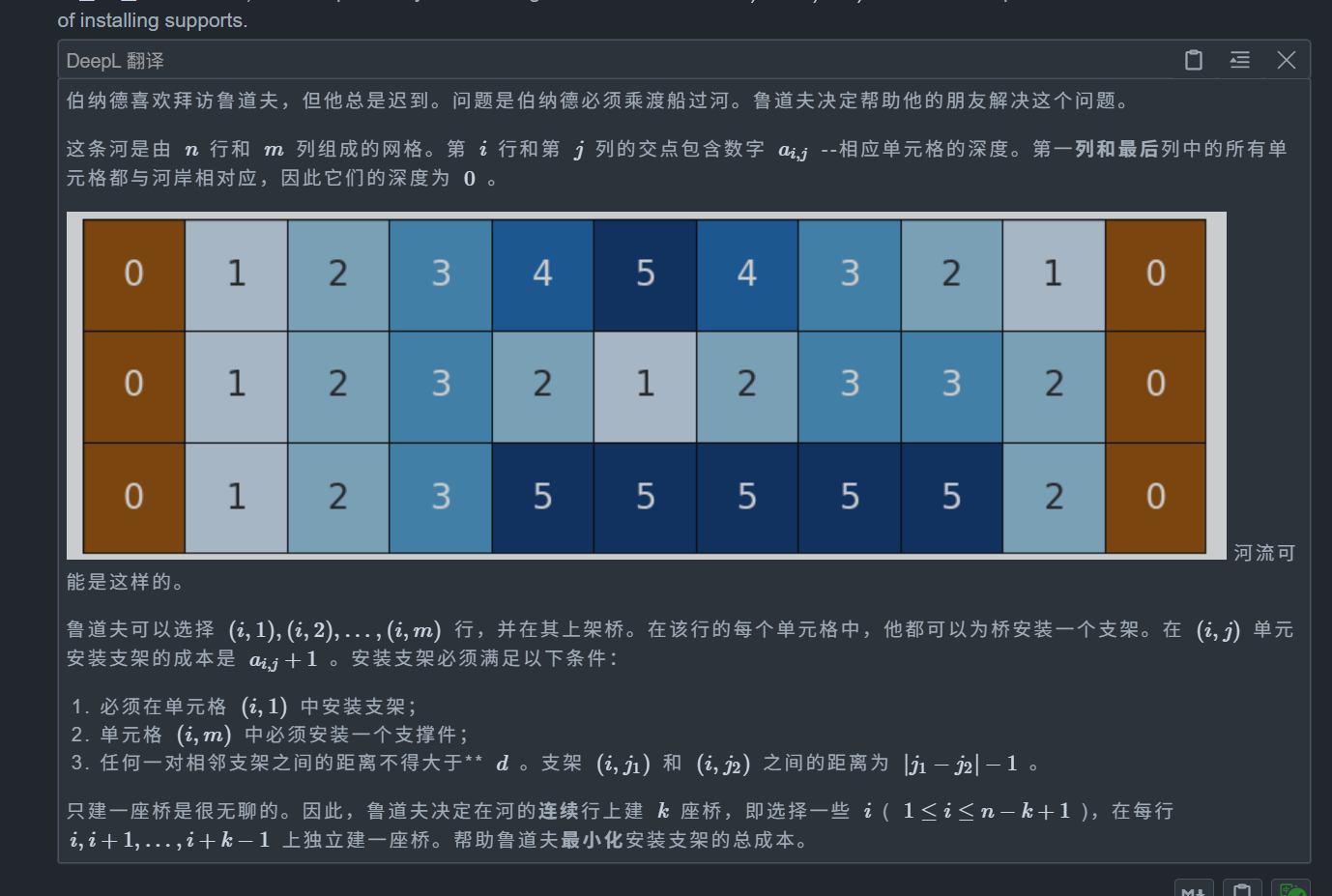
E. Rudolf and k Bridges

题目：

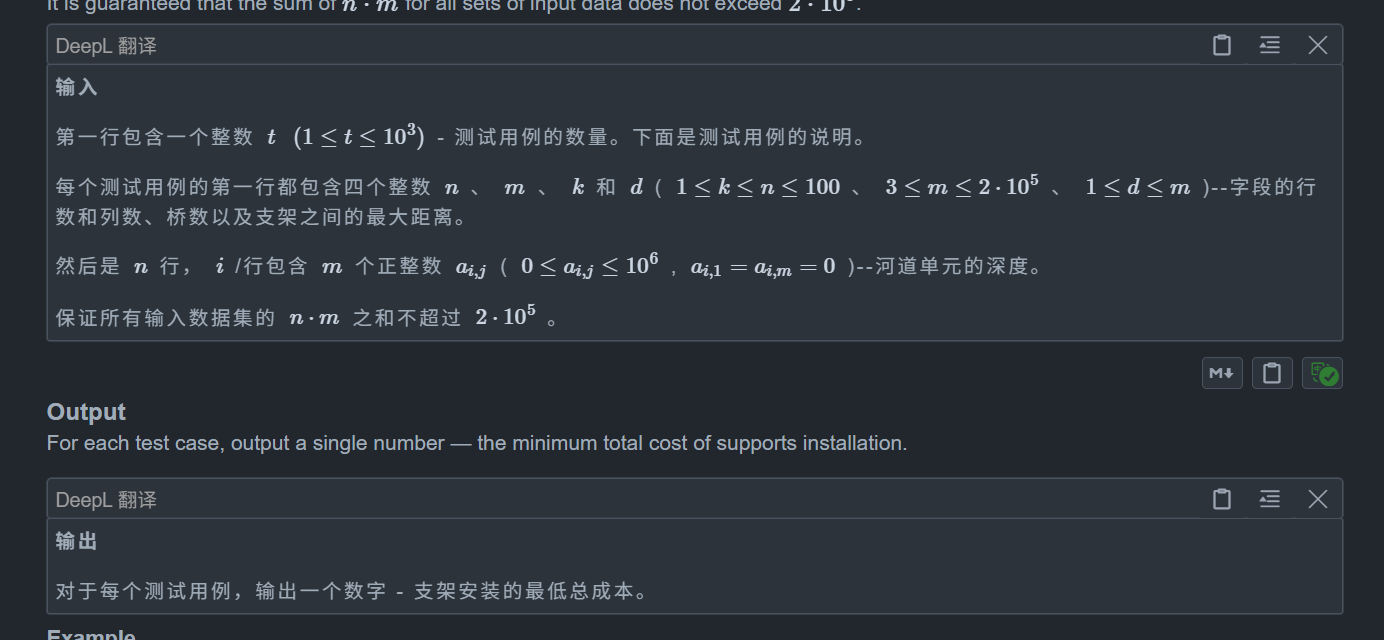思路：

单调队列优化DP

简单题，只需要看出这是一个单调队列优化DP即可，唯一需要注意的就是我们首尾是必选的，所以单调队列需要稍微更改一下

最后答案取 dp[i][m] 即可，然后做一个前缀和枚举答案

代码：

#include <bits/stdc++.h>
using namespace std;
#define yes cout << "Yes\n"
#define no cout << "No\n"
int n, m, k, d;
int a[105][200005];
long long dp[105][200005];
long long sum[105];
void solve()
{cin >> n >> m >> k >> d;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> a[i][j];dp[i][j] = 1e18;}}for (int i = 1; i <= n; i++){deque<int> q;dp[i][1] = 1;q.push_back(1);for (int j = 2; j <= m; j++){if (q.size() && q.front() < j - d - 1)q.pop_front();dp[i][j] = dp[i][q.front()] + a[i][j] + 1;while (q.size() && dp[i][q.back()] >= dp[i][j])q.pop_back();q.push_back(j);}sum[i] = sum[i - 1] + dp[i][m];}long long ans = 1e18;for (int i = k; i <= n; i++){ans = min(ans, sum[i] - sum[i - k]);}cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

D. A BIT of an Inequality

题目：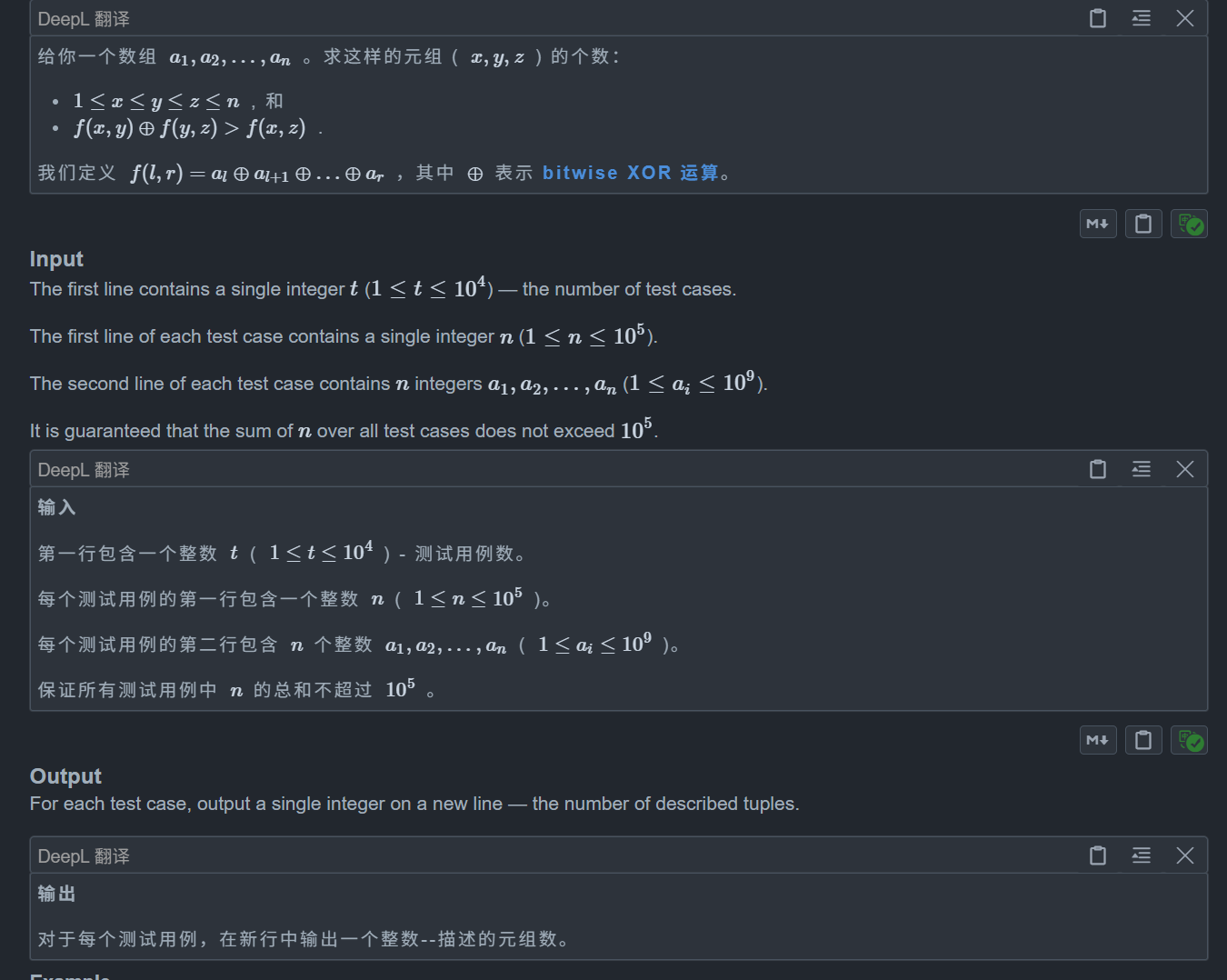

思路：

位运算 + 前缀和

题目简单明了，让我们化简一下看看

其实就是 sum[r] ^ s[l-1] ^ y > sum[r] ^ s[l-1]

也就是说我们要找到一个 y 满足上面的条件，对于这个 y，我们只看最高位，如果 y 最高位的 1 对于着的是 1，那么 sum 就会减少，且就算后面的 1 全做了奉献也是减少的，所以我们只考虑最高位的 1 是否对应着 0（关键点：只考虑最高位，一开始还没想出来）

所以我们考虑枚举 y，然后寻找 y 左边和右边的 sum 中有哪些满足 0/1 位的，那么结果就是 l0 * r0 + l1 * r1，因为 0 ^ 0 = 0，1 ^ 1 = 0，0 ^ 1 = 1

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"
const int N = 1e5 + 5;
int n;
int a[N];
int sum[N];
int getw(int x)
{for (int i = 32; i >= 0; i--){if (x >> i & 1)return i;}
}void solve()
{cin >> n;vector<vector<int>> sum1(n + 1, vector<int>(35, 0));for (int i = 1; i <= n; i++){cin >> a[i];sum[i] = sum[i - 1] ^ a[i];for (int j = 32; j >= 0; j--){sum1[i][j] = sum1[i - 1][j];if (sum[i] >> j & 1)sum1[i][j]++;}}int ans = 0;for (int i = 1; i <= n; i++){int w = getw(a[i]);int l1 = sum1[i - 1][w];int l0 = i - l1;int r1 = sum1[n][w] - sum1[i - 1][w];int r0 = n - i + 1 - r1;ans += r1 * l1 + r0 * l0;}cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

I. Disks

题目：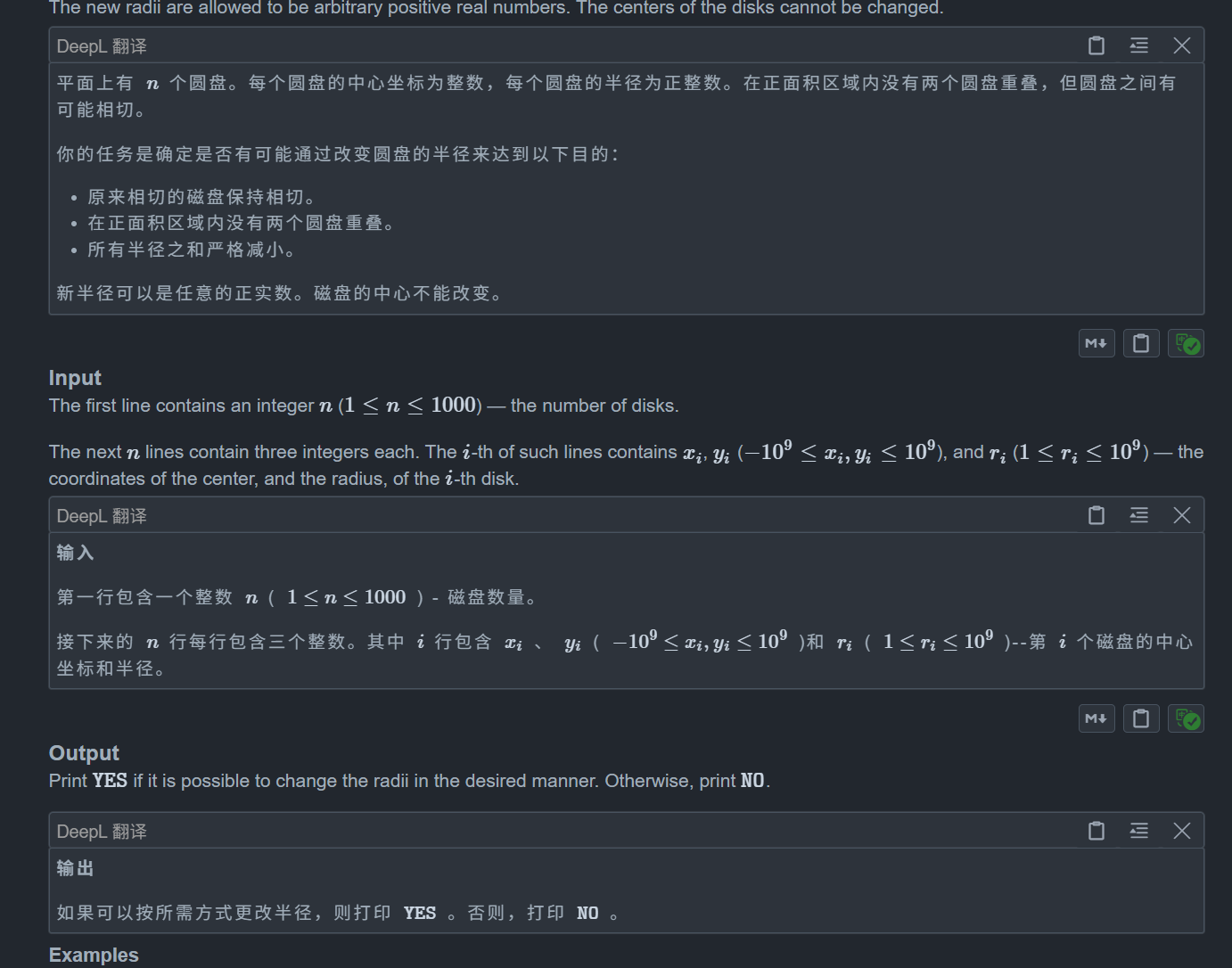

思路：

二分图判断

这题关键点在于能否想到二分图

注意到我们只考虑相切的圆，对于相切的圆，如果我们改变一个半径，那么另一个半径固然改变，且二者的半径和是不会变的

所以不妨考虑二分图，左边点为减少点，右边点为增加点

如果左边点和右边点数量一样，那么显然是和固定的，否则一定可以改变的，因为我们只需要让变小的半径多于变多的半径即可

官方题解：

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"int n;
int x[1005], y[1005], r[1005];
vector<vector<int>> g(1005);
int col[1005];
int cnt[2];
int ans = 0;
void dfs(int fa, int co)
{col[fa] = co;cnt[co]++;for (auto &son : g[fa]){if (col[son] == -1){dfs(son, 1 - co);}else if (col[son] != 1 - co){ans = 0;}}
}bool check(int i, int j)
{return (pow(x[i] - x[j], 2) + pow(y[i] - y[j], 2)) == (pow(r[i] + r[j], 2));
}void solve()
{cin >> n;for (int i = 1; i <= n; i++){cin >> x[i] >> y[i] >> r[i];}for (int i = 1; i <= n; i++){for (int j = i + 1; j <= n; j++){if (check(i, j)){g[i].push_back(j);g[j].push_back(i);}}}memset(col, -1, sizeof(col));for (int i = 1; i <= n; i++){if(col[i] == -1){cnt[0] = cnt[1] = 0;ans = 1;dfs(i,0);if(ans && cnt[0] != cnt[1]){yes;return;}}}no;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}

D. Tandem Repeats?

题目：

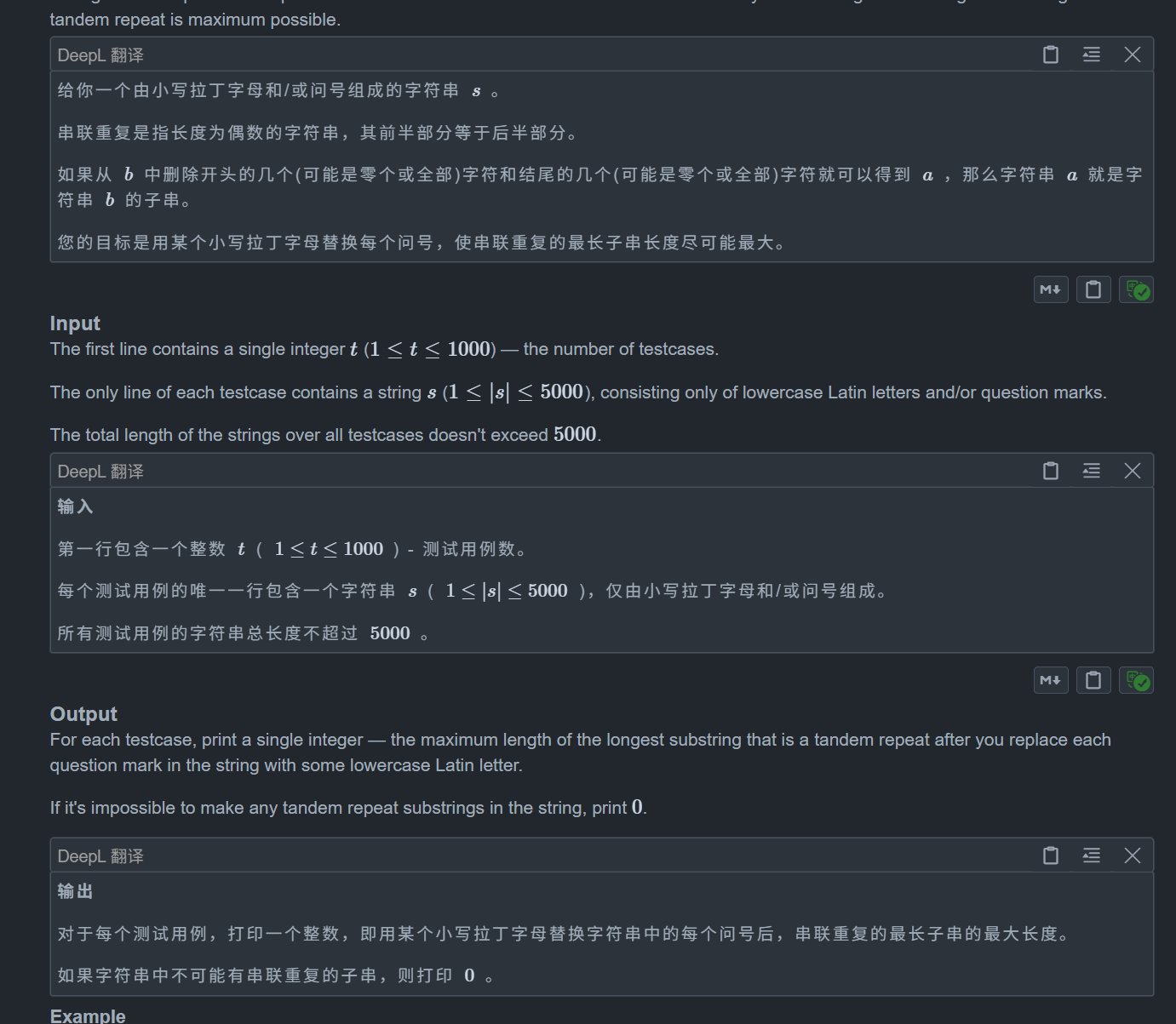
思路：

暴力枚举

本题其实暴力枚举即可，就是需要注意一些细节

我们枚举长度 len，对于 i，如果 i 和 i + len / 2 相同或者其中有一个是 ‘?' ，那我们就记 f + 1，否则 f = 0，只要 f * 2 = len 就说明我们已经凑够了，此时直接输出结果即可

非常巧妙的判断方法，特别注意别枚举出界即可

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"void solve()
{string s;cin >> s;for (int len = s.size() - s.size() % 2; len >= 0; len-=2){int f = 0;for (int i = 0; i+len/2 < s.size(); i++){if(f*2==len){break;;}if(s[i + len/2] == s[i] || s[i] == '?' || s[i+len/2] == '?'){f++;}else{f = 0;}}if(f *2 == len){cout << len << endl;return;}}
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

查看全文

http://www.dtcms.com/a/301409.html