Deja Vu: 利用上下文稀疏性提升大语言模型推理效率

温馨提示：
本篇文章已同步至"AI专题精讲" Deja Vu: 利用上下文稀疏性提升大语言模型推理效率

摘要

拥有数百亿参数的大语言模型（LLMs）催生了一系列令人振奋的 AI 应用。然而，在推理阶段它们计算开销极大。稀疏化是一种自然的降本策略，但现有方法要么需要代价高昂的重新训练，要么必须放弃 LLM 的“in-context learning”能力，要么在现代硬件上无法带来真实的墙钟时间加速。我们提出**上下文稀疏性（contextual sparsity）**这一假设：即存在一组依赖于输入的小规模注意力头和 MLP 参数集合，它们在保持输出质量接近 dense 模型的前提下，显著降低计算成本。我们证明了上下文稀疏性的存在，展示了它是可被准确预测的，并进一步提出了一种无需牺牲模型质量或上下文学习能力、即可在墙钟时间上加速推理的新方法。

基于这些洞察，我们提出了 DEJAVU 系统：该系统采用低开销算法，在每层接收输入时实时预测上下文稀疏性，并结合异步且硬件友好的实现方案，实现 LLM 推理加速。我们实验证实，DEJAVU 能够将 OPT-175B 的推理延迟在不影响模型质量的前提下，相比现有最优的 FasterTransformer 实现减少 2 倍以上的延迟，相比 Hugging Face 实现提升超 6 倍。代码已开源于：https://github.com/FMInference/DejaVu

1 引言

大型语言模型（LLMs），如 GPT-3、PaLM 和 OPT，已经展示出随着参数规模激增，模型性能和涌现出的 in-context learning 能力得到了显著提升——它们可以仅通过输入-输出示例来完成任务，而无需更新参数（Bommasani 等，2021；Liang 等，2022；Brown 等，2020；Min 等，2022；Chan 等，2022）。然而，这些模型在推理阶段的计算开销非常高，尤其是在面向低延迟的实际应用场景中（Pope 等，2022）。理想的推理阶段模型应在不牺牲性能和 LLM 特性的前提下，尽可能减少计算量与显存占用。最简单且自然的做法是稀疏化（sparsification）或剪枝（pruning），这在 LLM 出现之前已有悠久历史（LeCun 等，1989）。

遗憾的是，要在不损失质量和上下文学习能力的前提下，实现大型语言模型的稀疏化推理，并获得真实的墙钟时间加速，仍是一项巨大挑战。

尽管稀疏性和剪枝已经被广泛研究，但它们在 LLM 中未被广泛采用，主要是由于在现代硬件（如 GPU）上的质量与效率权衡不佳。一方面，在百亿级参数规模下进行重新训练或迭代剪枝几乎不可行，因此基于迭代剪枝和 lottery ticket hypothesis 的方法（Lee 等，2018；Frankle & Carbin，2018）仅适用于小规模模型。另一方面，要找到在保留上下文学习能力的同时实现稀疏性的结构也非常困难。尽管已有研究展示了基于任务的剪枝策略有效（Michel 等，2019；Bansal 等，2022），但为每个任务维护一个单独模型显然违背了 LLM 所追求的任务无关性目标。

此外，由于非结构化稀疏性在现代硬件上难以优化（Hooker，2021），实现墙钟时间加速尤为困难。例如，近期的零样本剪枝方法 SparseGPT（Frantar & Alistarh，2023）虽然可达到 60% 的非结构化稀疏率，但仍无法带来推理时间的实际加速。

因此，一个理想的 LLM 稀疏化方案应满足以下三个条件：

1. 无需重新训练模型；
2. 保持模型质量和上下文学习能力；
3. 在现代硬件上带来真实的墙钟时间加速。

为满足这些严苛要求，我们跳出传统的静态稀疏（如结构化/非结构化权重剪枝）框架，提出了新的视角：上下文稀疏性（contextual sparsity）。我们设想，对于任意输入，总存在一组小型、输入依赖的注意力头和 MLP 参数集合，其在不显著损失精度的情况下，可以输出与 dense 模型近似的结果。这一设想受到 LLM、隐马尔可夫模型（HMM）（Xie 等，2022；Baum & Petrie，1966）以及经典的维特比算法（Viterbi，1967）之间联系的启发。

我们提出：对一个预训练的 LLM，给定任何输入，其对应的上下文稀疏性是存在的。

该假设一旦成立，将使我们能够在推理时动态裁剪特定的注意力头和 MLP 参数（即结构化稀疏），而无需修改预训练模型。然而，实现这一目标面临三项挑战：

• 存在性：验证此类上下文稀疏性是否存在并非易事，直接验证的计算开销可能极其高昂。
• 可预测性：即使上下文稀疏性确实存在，如何在推理前准确预测特定输入对应的稀疏模式仍然具有挑战性。
• 效率：即使能正确预测稀疏模式，是否真的能在端到端墙钟时间上实现加速也是一个难题。以 OPT-175B 为例，其单个 MLP 模块在 8×A100 80GB 的机器上仅需 0.2 毫秒。如果没有快速的预测算法与优化的执行实现，这种方法的开销甚至可能拖慢推理速度，而非加速。

在本工作中，我们通过以下方式解决上述挑战：

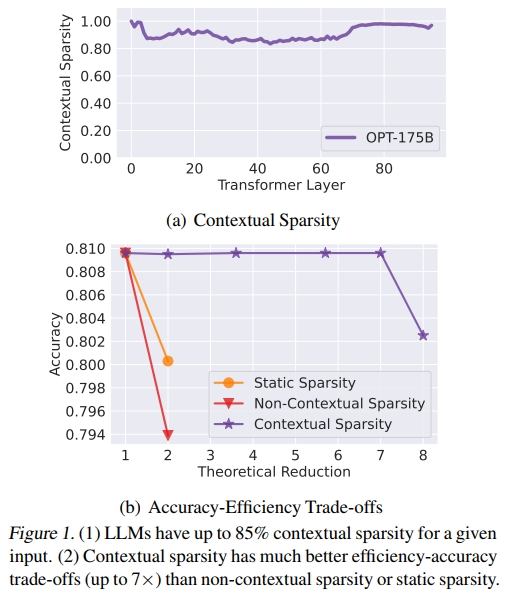
• 存在性：幸运的是，我们通过一种出人意料地简单的方法验证了上下文稀疏性的存在。为了实现与完整模型几乎一致的输出，上下文稀疏性平均可达到 85% 的结构化稀疏率，这意味着在特定输入下，参数量最多可减少 7 倍，同时保持模型精度（见图 1(a)）。
  在探索上下文稀疏性的过程中，我们获得了一些重要的经验观察，并对 LLM 的主要组成模块建立了理论认识，从而为解决预测和效率问题奠定了基础。
  

预测：我们发现，上下文稀疏性不仅依赖于单个输入 token（即非上下文的动态稀疏性），还依赖于 token 之间的交互关系（即上下文动态稀疏性）。如图 1(b) 所示，若仅依赖纯粹的动态信息，稀疏性预测将不准确。只有当 token embedding 中包含了足够的上下文信息时，才能准确预测稀疏性。我们还发现，每一层的上下文动态稀疏性可由**该层参数（如 attention head 或 MLP）与上一层输出之间的“相似度”**进行预测，而该输出本身携带了 token embedding 的即时上下文混合信息。

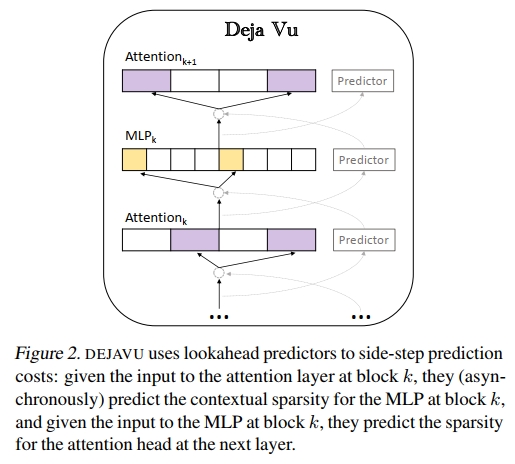
效率：由于推理时模型参数是静态的，我们受经典的最近邻搜索（Nearest Neighbor Search, NNS）文献及其在高效深度学习中的应用启发，提出将上述基于相似度的预测问题转化为 NNS 问题（Indyk & Motwani, 1998b；Zhang et al., 2018；Chen et al., 2020a）。然而，如前所述，在每层前都执行动态预测可能带来显著开销，难以获得整体加速效果。幸运的是，我们发现 LLM 存在一个现象，即由于残差连接的存在，token embedding 在不同层之间变化缓慢（这一现象在计算机视觉领域已广为人知（He et al., 2016））。由于多个连续层的输入相似度较高，我们设计了一种异步的前瞻式预测器（见图 2）。

基于上述发现，我们提出了一个系统 DEJAVU，其利用上下文稀疏性来实现适用于低延迟应用场景的高效 LLM 推理。

• 在第 4.1 节和第 4.2 节中，我们提出了一种低开销的基于学习的算法，用于在线预测稀疏性。对于特定层的输入，它预测下一层中需要使用的 attention head 或 MLP 参数的子集，并仅加载这些参数用于计算。
• 在第 4.3 节中，我们设计了一个异步预测器（类似于经典的分支预测器（Smith, 1998）），以避免顺序执行带来的额外开销。我们还提供了理论保证，说明跨层设计足以实现准确的稀疏性预测。
• 在第 4.4 节中，我们集成了面向硬件优化的稀疏矩阵乘法实现。DEJAVU（主要用 Python 实现）在不降低模型质量的前提下，相较于由 Nvidia 全 C++/CUDA 实现的最新库 FasterTransformer，在如 OPT-175B 等开源 LLM 上端到端推理延迟降低超过 2 倍，相较 Hugging Face 的广泛使用实现，在小 batch size 下也提升超过 2 倍。

此外，我们还对 DEJAVU 各组件进行了消融实验，并验证其与量化技术的兼容性。

2 相关工作与问题表述

我们首先简要回顾有关高效推理的大量研究文献，随后介绍本研究设置下的延迟分解，最后给出正式的问题表述。

2.1 用于推理的量化、剪枝与蒸馏

在机器学习推理中，各种简化技术已经被研究了数十年，主要包括三大类方法：量化（Han et al., 2015；Jacob et al., 2018；Nagel et al., 2019；Zhao et al., 2019）、剪枝或稀疏化（Molchanov et al., 2016；Liu et al., 2018；Hoefler et al., 2021）以及蒸馏（Hinton et al., 2015；Tang et al., 2019；Touvron et al., 2021）。这三类方法相互独立，通常在不同场景下发挥各自优势。近年来，越来越多的研究致力于将这些技术单独或组合应用于 LLM 推理（Yao et al., 2022；Park et al., 2022；Dettmers et al., 2022；Frantar et al., 2022；Frantar & Alistarh, 2023；Bansal et al., 2022；Xiao et al., 2022）。更详细的讨论见附录 A。

2.2 LLM 推理延迟分解

LLM 的生成过程通常包括两个阶段：

1. Prompt 阶段：处理输入序列，生成每个 transformer block 所需的 key 和 value（即 KV cache），这一过程类似于模型训练中的前向传播；
2. token 生成阶段：利用并更新 KV cache，逐步生成 token，其中当前 token 的生成依赖于此前生成的 token。

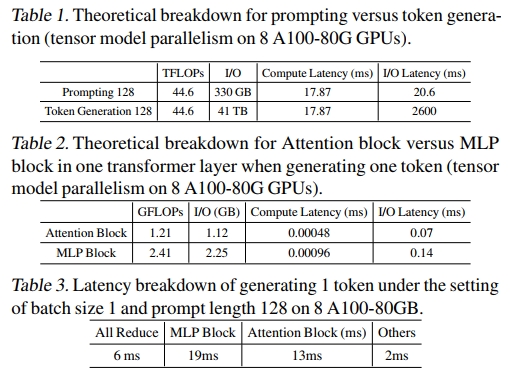
本文主要研究第二阶段，即 token 生成阶段，其往往在端到端推理时间中占据主导地位。如表 1 所示，生成长度为 128 的序列比处理相同长度的 prompt 序列所需时间更长，主要原因在于加载模型参数时存在 I/O 延迟。

此外，表 2 表明，在 LLM 中 attention 和 MLP 是两个主要瓶颈。例如在 175B 模型中，MLP 参数加载约占总 I/O 的三分之二，attention head 则占三分之一。

进一步地，在 tensor-parallel 设置下，每次前向传播中存在两个 GPU 间通信过程：一次发生在 attention block 之后，另一次发生在 MLP block 之后。如表 3 所示，GPU 之间的通信大约占生成一个 token 所需总时间的 15%。因此，本文的优化目标是使 attention 和 MLP 更高效。需要注意的是，即便完全跳过 transformer blocks，通信成本也意味着理论加速上限约为 6 倍。

2.3 问题表述

本研究的目标是通过利用 contextual sparsity 来减少 LLM 的生成延迟。下面我们将形式化定义被稀疏化的 attention 和 MLP blocks。

稀疏化的 MLP：一个 MLP block 中包含两个线性层，分别为 $W^1,W^2\in {\mathbb{R}}^{d\times 4d}$。设 $y\in {\mathbb{R}}^{1\times d}$ 为当前生成步骤中输入到 MLP block 的向量。令每一列（即第 $i$ 个神经元的权重）为 $W_i^1,W_i^2\in {\mathbb{R}}^{d\times 1}$。在 contextual sparsity 的设定下，仅需其中一小部分参与计算。设 $S_M\subseteq [4d]$ 为针对输入 $y$ 选择的神经元索引集合，则稀疏化的 MLP 计算方式为：
$${\mathsf{MLP}}_{S_M}(y)\stackrel{\cdot }{=}\sigma (y{W}_{S_M}^1)(W_{S_M}^2{)}^{\top }(1)$$

其中 $\sigma$ 是激活函数，例如 ReLU 或 GeLU。需要注意的是，由于第一层线性变换产生的是稀疏激活，因此第二层线性变换也自然是稀疏化的。

稀疏化的 Attention：设 $X\in {\mathbb{R}}^{n\times d}$ 表示所有 token（如 prompt 和此前生成的 token）的 embedding。令 $y\in {\mathbb{R}}^{1\times d}$ 表示当前生成步骤中输入到 Multi-Head-Attention（MHA）的向量。假设共有 $h$ 个 attention head。对于每个 $i\in [h]$，设 $W_i^K,W_i^Q,W_i^V\in {\mathbb{R}}^{d\times d_h}$ 为该 head 的 key、query 和 value 映射矩阵，$W_i^O\in {\mathbb{R}}^{d_h\times d}$ 为输出映射矩阵。

在 contextual sparsity 的设定下，设 $S_A$ 为一组经过选择、能对输入 $y$ 产生近似于完整 attention 输出的小规模 attention head 的索引集合。参考 (Alman & Song, 2023) 的记号系统，稀疏化的 MHA 计算可形式化地写作：
$${\mathsf{MHA}}_{S_A}(y)=\sum _{i\in S_A}\underset{1\times d_h{d}_h\times d}{\underbrace{H_i(y)W_i^O}}$$
其中，$H_i(y):{\mathbb{R}}^d\to {\mathbb{R}}^{d_h}\mathrm{and}{D}_i(y)\in \mathbb{R}$ ，可以被写作
$$H_i(y):=D_i(y{)}^{-1}\exp (y{W}_i^Q(W_i^K{)}^{\top }{X}^{\top })X{W}_i^V(2)$$

$$D_i(y):=\exp (y{W}_i^Q(W_i^K{)}^{\top }{X}^{\top })1_n$$

对于 MLP 和 Attention，两者而言，在给定计算预算的前提下，目标是寻找集合 $S_M$ 和 $S_A$，使得稀疏近似与完整计算之间的误差最小。

3 预训练大语言模型具有上下文稀疏性

在本节中，我们展示了大语言模型（LLMs）中稀疏性的几个关键观察结果与理论理解，这些构成了 DEJAVU 设计的基础。我们首先在第 3.1 节测试“上下文稀疏性假说”，验证预训练 LLM 中确实存在上下文稀疏性。接着在第 3.2 节中，我们解释为什么即便在密集训练的情况下，上下文稀疏性也会自然出现。最后，在第 3.3 节中我们展示了关于残差连接（residual connection）的一个观察，并从分析角度解释它与上下文稀疏性的关系。

3.1 上下文稀疏性假说

受之前剪枝研究（Molchanov et al., 2016）启发，我们发现有一个令人惊讶的简单方法可以用来研究并验证我们的假说。本节将介绍这一测试过程、具体观察以及由此得到的启发。

验证过程：
我们在 OPT-175B、66B 和 30B 模型上进行了测试，使用的数据集包括 OpenBookQA（Mihaylov et al., 2018）和 Wiki-Text（Merity et al., 2016）等多个下游任务数据。我们对每个输入样本进行两次前向传播来寻找其对应的上下文稀疏结构。在第一次前向传播中，我们记录一部分参数，具体来说是哪些 attention head 和 MLP 神经元在该输入下输出范数较大。接着，在第二次前向传播中，我们仅使用第一次中记录到的这部分参数来进行计算。令人惊讶的是，这两次前向传播在所有的 in-context learning 任务和语言建模任务中都达到了类似的预测准确率或性能，验证了上下文稀疏性在预训练大模型中确实存在。

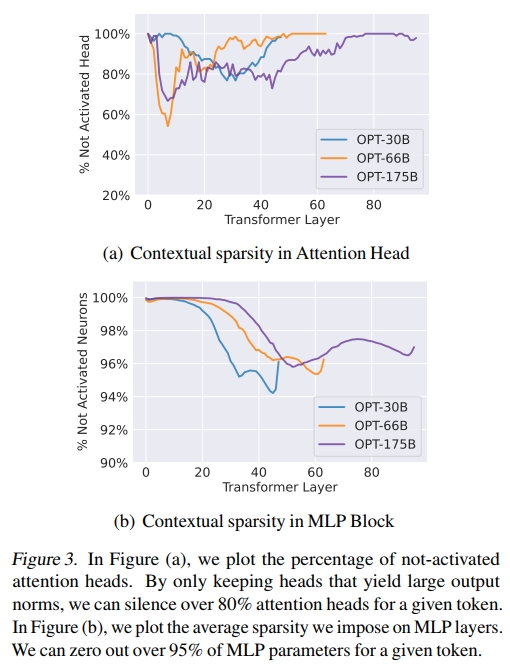
观察结果： 图 3 显示，我们平均可以对 attention head 施加高达 80% 的稀疏性，对 MLP 神经元施加高达 95% 的稀疏性。如第 2 节所述，OPT-175B 模型中 MLP 的参数量是 attention block 的 2 倍，因此总体稀疏率约为 85%。由于这里所用的稀疏性都是结构化的（即 head 和神经元级别的稀疏），如果能够准确地预测这些稀疏结构，理论上可能实现 7 倍的加速。

洞察： 在推理阶段，我们能够在 MLP block 中发现上下文稀疏性是较为直观的，因为这些模块使用了激活函数（例如 ReLU 或 GeLU（Kurtz et al., 2020））。类似的现象也在 Li 等人（2022）的研究中被观察到。

然而，在 attention 层中发现上下文稀疏性则颇为出人意料。需要注意的是，在 attention 中发现上下文稀疏性不同于传统的 head 剪枝（head pruning）。我们进行交叉验证后发现，不同的输入样本具有不同的上下文稀疏模式。尽管对于某个样本来说，约 80% 的 attention head 没有被使用，但这些 head 可能会在其他样本中被使用。接下来，我们将尝试解释为什么在 attention block 中也会自然地产生上下文稀疏性。

3.2 Attention 层中的 Token 聚类现象

在上一节中，我们已经验证，对于给定的输入，大型语言模型（LLMs）中确实存在上下文稀疏性。本节我们尝试理解这一现象产生的原因，特别是在 attention 层中的表现。我们首先展示一个关于 attention 的深入观察，接着提出一个假设：self-attention 在本质上是一种聚类算法，最后我们给出分析性的证据来支持这一假设。

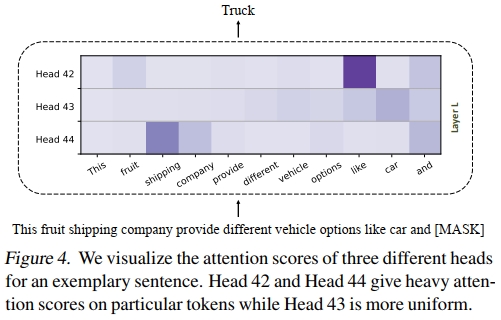
观察： 图 4 显示了在同一层中，三个不同 attention head 的 attention map，输入是一个示例文本，当前模型需要预测的下一个 token 是 “Truck”。图中颜色越深表示 attention 分数越高。

我们观察到：

• 中间的 head 是一个**相对均匀混合（token-mixing）**的 head，即它将注意力较平均地分配给所有 token。
• 上方和下方的两个 head 则是“重点关注（heavy hitter）”的 head，分别对 token “like” 和 “shipping” 表现出较高的 attention 分数。

这种现象并不令人意外：即使只保留重点关注的 head 而丢弃那些均匀分布的 head，也不会影响模型的预测性能，因为那些均匀的 head 没有捕捉或编码重要的 token 间交互。

在下一节中，我们还将进一步解释：如何根据 attention head 是否均匀、或者其输出范数是否较小来选择保留或丢弃该 head，并说明这两个标准之间存在高度相关性。

假设：注意力头执行均值迁移聚类（Mean-Shift Clustering）

我们假设每个注意力头（attention head）执行的操作类似于均值迁移聚类（Derpanis, 2005）。

回顾第2.3节中的符号定义：对于当前层的第 i 个注意力头，令

• $X=[x_1,\dots ,x_n{]}^{\top }\in {\mathbb{R}}^{n\times d}$ 表示前一时间步的所有 token 嵌入（token embeddings），
• $X{W}_i^K$ 和 $X{W}_i^V$ 分别表示对应的 key 和 value 投影矩阵乘积。

对于输入的嵌入 $y$，输出为 ${\tilde{y}}_i=H_i(y)$，其中 $H_i(y)$ 的定义见等式(2)。

对于每个 $i\in [h]$，定义相似度函数：

$$K_i(x_j,y):=\exp (y{W}_i^Q(W_i^K{)}^{\top }{x}_j)$$

用于衡量向量 $x_j$ 与 $y$ 之间的相似度。

定义均值迁移操作：

$$m_i(y):=\frac{{\sum }_j{K}_i(x_j,y)x_j}{{\sum }_j{K}_i(x_j,y)}$$

即基于相似度加权的 $x_j$ 的加权平均。由此，注意力头的输出为：

$${\tilde{y}}_i=m_i(y)W_i^V$$

进一步假设：令$W_i^V=I$ ，（单位矩阵），并考虑残差连接（residual connection）和层归一化（layer norm），那么下一层当前 token 的嵌入更新为：

$${\hat{y}}_i=\text{Normalize}(y+{\tilde{y}}_i)=\text{Normalize}(y+m_i(y))$$

这个迭代过程存在一个固定点：$y=\gamma m_i(y)$ ，其中 $\gamma$ 是任意标量。

这个过程类似于均值迁移聚类（mean-shift clustering），其核心思想是通过不断迭代：$y\leftarrow m_i(y)$ ，直到收敛到固定点。该固定点满足：$y=m_i(y)$ 。

温馨提示：
阅读全文请访问"AI深语解构" Deja Vu: 利用上下文稀疏性提升大语言模型推理效率