当前位置： 首页 > news >正文

蜣螂优化算法的华丽转身：基于Streamlit的MSIDBO算法可视化平台

news 2025/7/28 9:16:59

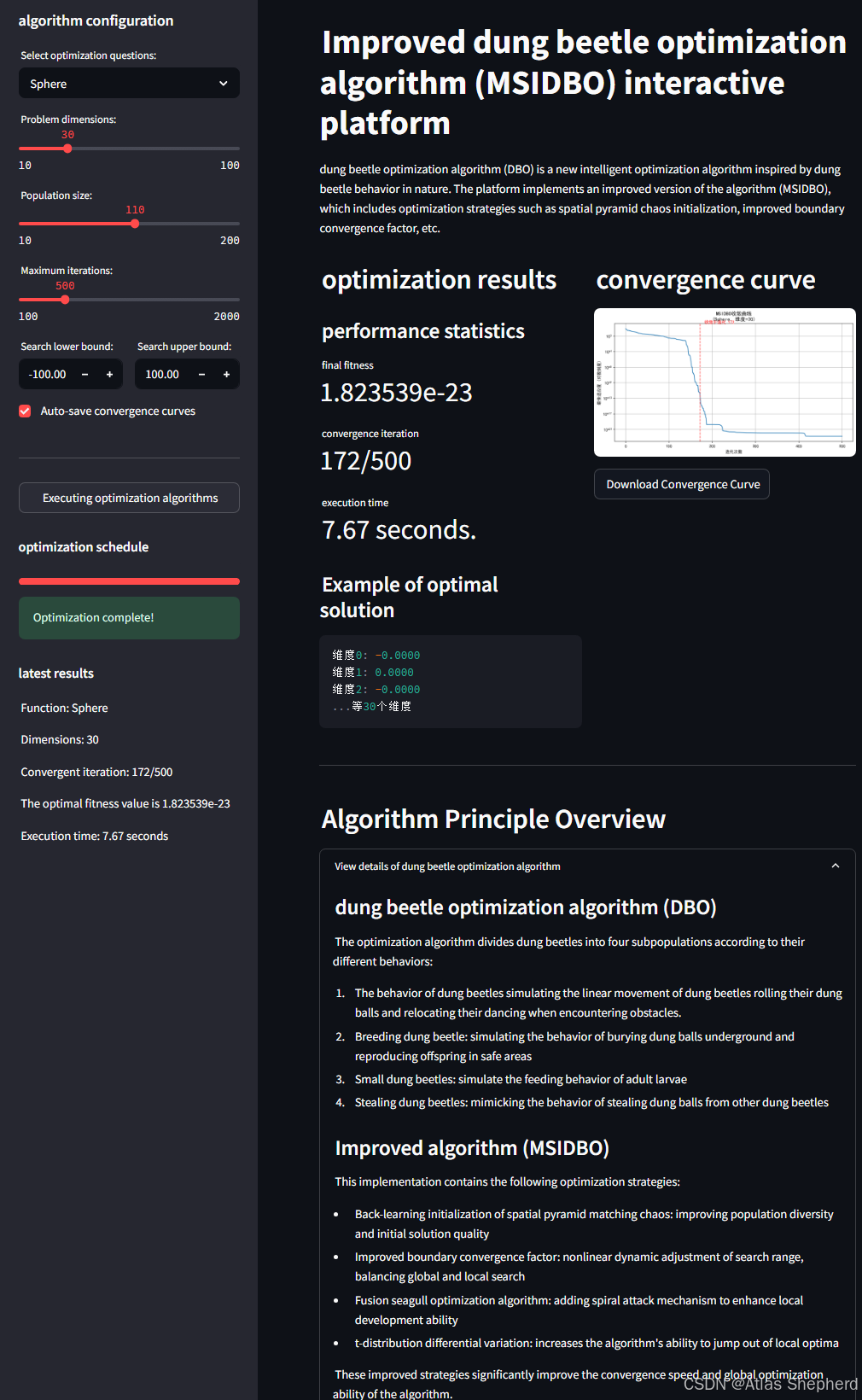
基于Streamlit的交互式Web应用，用于展示和运行改进的蜣螂优化算法（MSIDBO）。以下是代码的详细解读，分模块说明其功能和实现细节：

1. 算法核心：MSIDBO类（未完整展示）

虽然代码中未完整展示MSIDBO类的实现，但通过run_optimization函数的调用可以推断其结构：

  • MSIDBO类定义：包含算法的核心逻辑，如种群初始化、迭代优化、收敛判断等。
  • 关键方法：
    • __init__: 初始化参数（目标函数、维度、搜索边界、种群大小、最大迭代次数等）。
    • run: 执行优化过程，返回最优解（best_solution）、最优适应值（best_fitness）和收敛历史（history）。
  • 算法改进点（根据代码注释）：
    • 空间金字塔混沌初始化：提高种群多样性。
    • 改进边界收敛因子：动态调整搜索范围，平衡全局与局部搜索。
    • 融合海鸥优化的螺旋攻击机制：增强局部开发能力。
    • t-分布差分变异：增加跳出局部最优的能力。

2. Streamlit Web应用结构

代码使用Streamlit构建交互式界面，分为以下几个模块：

(1) 页面配置
st.set_page_config( page_title="🐞 改进蜣螂优化算法平台", page_icon="🐞", layout="wide" )
  • 设置页面标题、图标和布局为宽屏模式。
(2) 侧边栏配置
  • 问题选择：通过下拉菜单选择优化目标函数（如Sphere、Rosenbrock等）。
  • 参数配置：
    • 维度（dimension）
    • 种群大小（population_size）
    • 最大迭代次数（max_iter）
    • 搜索边界（仅对部分函数开放）
  • 执行按钮：触发run_optimization函数运行算法。
  • 状态显示：展示最新运行结果（如收敛迭代次数、最优适应值、执行时间等）。
(3) 主界面布局
  • 左侧列（优化结果）：
    • 显示性能统计（最终适应值、收敛迭代次数、执行时间）。
    • 展示最优解的示例（前三个维度的值）。
  • 右侧列（收敛曲线）：
    • 使用matplotlib绘制对数坐标收敛曲线，展示最佳适应度随迭代的变化。
    • 提供下载收敛曲线的功能。

3. 核心功能：run_optimization函数

def run_optimization():# 创建MSIDBO实例optimizer = MSIDBO(objective_func=TEST_FUNCTIONS[function_name],dim=dim,lb=lb,ub=ub,population_size=population_size,max_iter=max_iter,verbose=False)# 运行算法start_time = time.time()best_solution, best_fitness, history = optimizer.run()exec_time = time.time() - start_time# 保存结果到session_statestats = {"function": function_name,"dimension": dim,"convergence_iter": optimizer.convergence_iter,"execution_time": exec_time,"final_fitness": best_fitness,"population_size": population_size}st.session_state.stats = statsst.session_state.history = historyst.session_state.solution = best_solution# 绘制收敛曲线fig, ax = plt.subplots(figsize=(10, 5))ax.semilogy(history)ax.set_title(...)ax.grid(True)# 标记收敛点（若有）if optimizer.convergence_iter > 0:ax.axvline(...)ax.text(...)st.session_state.convergence_plot = fig
  • 功能：
    • 实例化MSIDBO优化器。
    • 运行算法并记录执行时间。
    • 保存结果到st.session_state供界面展示。
    • 生成收敛曲线并保存到st.session_state。

4. 收敛曲线绘制

  • 对数坐标图：使用ax.semilogy(history)绘制适应度变化，更清晰地展示收敛过程。
  • 收敛点标记：若算法在迭代中达到预设精度，用垂直线标记收敛点。

5. 界面交互与结果展示

  • 左侧列：
    • 显示性能统计（如final_fitness、execution_time）。
    • 展示最优解的示例值（前三个维度）。
  • 右侧列：
    • 动态生成收敛曲线。
    • 提供下载功能（通过st.download_button）。
import numpy as np
import streamlit as st
import matplotlib.pyplot as plt
from scipy.stats import t
import time
import base64
import io
import math
import matplotlib.font_manager as fm# 设置中文字体支持
try:# 尝试使用系统自带的中文字体plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'KaiTi', 'FangSong', 'STSong', 'STKaiti']plt.rcParams['axes.unicode_minus'] = False
except:# 如果系统没有中文字体，尝试使用matplotlib的默认字体plt.rcParams['font.sans-serif'] = ['DejaVu Sans']plt.rcParams['axes.unicode_minus'] = Falseclass MSIDBO:"""改进的蜣螂优化算法实现"""def __init__(self, objective_func, dim=30, lb=-100, ub=100, population_size=50, max_iter=500, K=0.5, u=1.0, v=1.0, S=1.0, w=0.5, verbose=True):"""初始化算法参数Parameters:objective_func (function): 目标函数dim (int): 问题维度lb (float or list): 下界ub (float or list): 上界population_size (int): 种群大小max_iter (int): 最大迭代次数K (float): 反向学习参数 (0,1)u (float): 螺旋形状常数v (float): 螺旋形状常数S (float): 偷窃蜣螂常数w (float): t分布变异的缩放因子verbose (bool): 是否打印迭代信息"""self.obj_func = objective_funcself.dim = dimself.lb = np.array(lb) if isinstance(lb, list) else np.full(dim, lb)self.ub = np.array(ub) if isinstance(ub, list) else np.full(dim, ub)self.pop_size = population_sizeself.max_iter = max_iterself.K = Kself.u = uself.v = vself.S = Sself.w = wself.verbose = verbose# 子种群比例self.roller_ratio = 0.4   # 滚球蜣螂self.breeder_ratio = 0.3  # 繁殖蜣螂self.minor_ratio = 0.2    # 小蜣螂self.thief_ratio = 0.1    # 偷窃蜣螂# 收敛迭代次数self.convergence_iter = -1# 计算结果存储self.g_best_pos = Noneself.g_best_fit = float('inf')self.fitness_history = []def spm_chaos_mapping(self):"""SPM混沌映射生成混沌序列 (向量化优化版本)"""# 参数设置eta = 0.4mu = 0.3pop = np.random.uniform(0, 1, (self.pop_size * 2, self.dim))# 迭代生成混沌序列 (减少到5次迭代)for _ in range(5):# 划分不同区域mask0 = (0 <= np.abs(pop)) & (np.abs(pop) < eta)mask1 = (eta <= np.abs(pop)) & (np.abs(pop) < 0.5)mask2 = (0.5 <= np.abs(pop)) & (np.abs(pop) < 1 - eta)mask3 = (1 - eta <= np.abs(pop)) & (np.abs(pop) < 1)# 分别处理不同区域的点pop[mask0] = np.mod(pop[mask0] / eta + mu * np.sin(np.pi * pop[mask0]) + np.random.random(pop[mask0].shape) * 0.01, 1)pop[mask1] = np.mod(pop[mask1] / (0.5 - eta) + mu * np.sin(np.pi * pop[mask1]) + np.random.random(pop[mask1].shape) * 0.01, 1)pop[mask2] = np.mod((1 - pop[mask2]) / (0.5 - eta) + mu * np.sin(np.pi * (1 - pop[mask2])) + np.random.random(pop[mask2].shape) * 0.01, 1)pop[mask3] = np.mod((1 - pop[mask3]) / eta + mu * np.sin(np.pi * (1 - pop[mask3])) + np.random.random(pop[mask3].shape) * 0.01, 1)return popdef map_to_solution_space(self, chaos_pop):"""将[0,1]映射到解空间"""return self.lb + (self.ub - self.lb) * chaos_popdef opposition_learning(self, population):"""反向学习生成反向解"""center = self.K * (self.lb + self.ub)return np.clip(center - population, self.lb, self.ub)def spm_chaos_opposition_init(self):"""SPM混沌反向学习初始化"""# SPM混沌映射生成种群spm_pop = self.spm_chaos_mapping()spm_pop = self.map_to_solution_space(spm_pop)# 反向学习生成种群opposite_pop = self.opposition_learning(spm_pop)# 合并种群并选择最优个体combined_pop = np.vstack([spm_pop, opposite_pop])fitness = np.array([self.obj_func(ind) for ind in combined_pop])sorted_indices = np.argsort(fitness)return combined_pop[sorted_indices[:self.pop_size]]def improved_R_factor(self, t):"""改进的边界收敛因子"""x = 2 * t / self.max_iter - 1return ((x**3 - 3*x + 2) / 4)def update_global_best(self, fitness):"""更新全局最优解"""min_idx = np.argmin(fitness)if fitness[min_idx] < self.g_best_fit:self.g_best_fit = fitness[min_idx]self.g_best_pos = self.population[min_idx].copy()# 首次达到接近0的精度时记录收敛if self.g_best_fit < 1e-12 and self.convergence_iter == -1:self.convergence_iter = self.current_iter + 1def roll_ball(self, i, Xw):"""滚球蜣螂更新"""# 90%概率滚球，10%概率跳舞if np.random.rand() < 0.9:# 滚球行为delta_x = self.population[i] - Xwalpha = np.random.choice([1, -1], size=self.dim)k = np.random.uniform(0, 0.2, size=self.dim)b = np.random.uniform(0, 1, size=self.dim)return self.population[i] + alpha * k * delta_x + b * delta_xelse:# 跳舞行为displacement = self.population[i] - self.prev_positions[i]theta = np.random.uniform(0, np.pi)# 避免theta接近π/2导致数值不稳定if np.abs(theta - np.pi/2) < 0.01:theta = np.pi/2 + 0.1return self.population[i] + np.tan(theta) * displacementdef breeder(self, i, R):"""繁殖蜣螂更新（融合海鸥螺旋攻击）"""# 计算边界L_star_b = np.maximum(self.g_best_pos * (1 - R), self.lb)U_star_b = np.minimum(self.g_best_pos * (1 + R), self.ub)# 海鸥螺旋攻击机制beta = np.random.uniform(0, 2 * np.pi)r = self.u * np.exp(beta * self.v)x_prime = r * np.cos(beta)y_prime = r * np.sin(beta)z_prime = r * betaspiral_factor = x_prime * y_prime * z_prime# 位置更新b1 = np.random.uniform(0, 1, size=self.dim)b2 = np.random.uniform(0, 1, size=self.dim)return self.g_best_pos + spiral_factor * (b1 * (self.population[i] - L_star_b) + b2 * (self.population[i] - U_star_b))def minor(self, i, R):"""小蜣螂更新"""# 计算边界L_bb = np.maximum(self.g_best_pos * (1 - R), self.lb)U_bb = np.minimum(self.g_best_pos * (1 + R), self.ub)# 位置更新C1 = np.random.randn()C2 = np.random.uniform(0, 1, size=self.dim)return self.population[i] + C1 * (self.population[i] - L_bb) + C2 * (self.population[i] - U_bb)def thief(self, i):"""偷窃蜣螂更新"""g = np.random.randn(self.dim)dist = np.abs(self.population[i] - self.g_best_pos)return self.g_best_pos + self.S * g * distdef t_distribution_mutation(self):"""t-分布差分变异"""new_pop = np.copy(self.population)new_fitness = np.copy(self.fitness)for i in range(self.pop_size):# 随机选择另一个体r = np.random.randint(self.pop_size)# 确保自由度有效df = max(1, self.current_iter)# t分布的随机数 (自由度为当前迭代次数)gamma1 = t.rvs(df=df, size=self.dim)gamma2 = t.rvs(df=df, size=self.dim)# 差分变异new_pos = self.population[i] + self.w * (gamma1 * (self.g_best_pos - self.population[i]) + gamma2 * (self.population[r] - self.population[i]))# 边界检查new_pos = np.clip(new_pos, self.lb, self.ub)# 贪婪选择new_fit = self.obj_func(new_pos)if new_fit < self.fitness[i]:new_pop[i] = new_posnew_fitness[i] = new_fitreturn new_pop, new_fitnessdef run(self):"""执行算法主循环"""# 初始化种群self.population = self.spm_chaos_opposition_init()self.prev_positions = np.copy(self.population)self.fitness = np.array([self.obj_func(ind) for ind in self.population])self.update_global_best(self.fitness)self.fitness_history.append(self.g_best_fit)self.convergence_iter = -1if self.verbose:print(f"Iter 1/{self.max_iter}, Best Fitness: {self.g_best_fit:.6f}")for t in range(self.max_iter):self.current_iter = t# 保存上一代位置（用于跳舞行为）self.prev_positions = np.copy(self.population)# 计算改进的R因子R = self.improved_R_factor(t)# 划分子种群roller_end = int(self.pop_size * self.roller_ratio)breeder_end = int(self.pop_size * (self.roller_ratio + self.breeder_ratio))minor_end = int(self.pop_size * (self.roller_ratio + self.breeder_ratio + self.minor_ratio))# 更新全局最差解位置worst_idx = np.argmax(self.fitness)Xw = self.population[worst_idx]# 更新滚球蜣螂for i in range(roller_end):new_pos = self.roll_ball(i, Xw)self.population[i] = np.clip(new_pos, self.lb, self.ub)# 更新繁殖蜣螂for i in range(roller_end, breeder_end):new_pos = self.breeder(i, R)self.population[i] = np.clip(new_pos, self.lb, self.ub)# 更新小蜣螂for i in range(breeder_end, minor_end):new_pos = self.minor(i, R)self.population[i] = np.clip(new_pos, self.lb, self.ub)# 更新偷窃蜣螂for i in range(minor_end, self.pop_size):new_pos = self.thief(i)self.population[i] = np.clip(new_pos, self.lb, self.ub)# 计算新适应度self.fitness = np.array([self.obj_func(ind) for ind in self.population])# 更新全局最优解self.update_global_best(self.fitness)# t-分布差分变异self.population, self.fitness = self.t_distribution_mutation()# 更新全局最优解（变异后）self.update_global_best(self.fitness)# 记录历史最优适应度self.fitness_history.append(self.g_best_fit)# 打印迭代信息if self.verbose and (t % 50 == 0 or t == self.max_iter - 1):print(f"Iter {t+1}/{self.max_iter}, Best Fitness: {self.g_best_fit:.6f}")return self.g_best_pos, self.g_best_fit, self.fitness_history# 测试函数集合
TEST_FUNCTIONS = {"Sphere": lambda x: np.sum(x**2),"Rastrigin": lambda x: 10 * len(x) + np.sum(x**2 - 10 * np.cos(2 * np.pi * x)),"Ackley": lambda x: 20 - 20 * np.exp(-0.2 * np.sqrt(np.mean(x**2))) + math.e - np.exp(np.mean(np.cos(2 * np.pi * x))),"Rosenbrock": lambda x: np.sum(100 * (x[1:] - x[:-1]**2)**2 + (1 - x[:-1])**2),"Schwefel": lambda x: 418.9829 * len(x) - np.sum(x * np.sin(np.sqrt(np.abs(x))))
}def run_optimization():"""执行优化算法并显示结果"""st.sidebar.subheader("优化进度")progress_bar = st.sidebar.progress(0)status_text = st.sidebar.empty()# 获取参数function_name = st.session_state.selected_functiondim = st.session_state.dimensionpop_size = st.session_state.population_sizemax_iter = st.session_state.max_iterlb = st.session_state.lower_boundub = st.session_state.upper_boundsave_plot = st.session_state.save_plot# 设置问题边界if function_name == "Schwefel":lb = -500ub = 500elif function_name == "Rosenbrock":lb = -30ub = 30# 创建优化器optimizer = MSIDBO(objective_func=TEST_FUNCTIONS[function_name],dim=dim,lb=lb,ub=ub,population_size=pop_size,max_iter=max_iter,verbose=False)# 运行优化算法start_time = time.time()best_solution, best_fitness, history = optimizer.run()exec_time = time.time() - start_time# 更新性能统计stats = {"function": function_name,"dimension": dim,"convergence_iter": optimizer.convergence_iter,"execution_time": exec_time,"final_fitness": best_fitness,"population_size": pop_size}# 保存结果st.session_state.stats = statsst.session_state.history = historyst.session_state.solution = best_solution# 绘制收敛曲线fig, ax = plt.subplots(figsize=(10, 5))ax.semilogy(history)ax.set_title(f'MSIDBO收敛曲线\n({function_name}, 维度={dim})')ax.set_xlabel('迭代次数')ax.set_ylabel('最佳适应度 (对数刻度)')ax.grid(True)if optimizer.convergence_iter > 0:ax.axvline(x=optimizer.convergence_iter, color='r', linestyle='--', alpha=0.7)ax.text(optimizer.convergence_iter + max_iter*0.02, plt.ylim()[1] * 0.9, f'收敛于迭代 {optimizer.convergence_iter}', color='r')st.session_state.convergence_plot = figstatus_text.success("优化完成!")progress_bar.progress(100)def main():st.set_page_config(page_title="蜣螂优化算法平台",page_icon="🐞",layout="wide")# 页面标题st.title("🐞 改进蜣螂优化算法(MSIDBO)交互平台")st.markdown("""**蜣螂优化算法(DBO)** 是一种受自然界蜣螂行为启发的新型智能优化算法。本平台实现了改进版算法(MSIDBO)，包含空间金字塔混沌初始化、改进边界收敛因子等优化策略。""")# 初始化session状态if 'stats' not in st.session_state:st.session_state.stats = Noneif 'history' not in st.session_state:st.session_state.history = Noneif 'solution' not in st.session_state:st.session_state.solution = Noneif 'convergence_plot' not in st.session_state:st.session_state.convergence_plot = Noneif 'selected_function' not in st.session_state:st.session_state.selected_function = "Sphere"if 'dimension' not in st.session_state:st.session_state.dimension = 30if 'population_size' not in st.session_state:st.session_state.population_size = 50if 'max_iter' not in st.session_state:st.session_state.max_iter = 500if 'lower_bound' not in st.session_state:st.session_state.lower_bound = -100if 'upper_bound' not in st.session_state:st.session_state.upper_bound = 100if 'save_plot' not in st.session_state:st.session_state.save_plot = False# 侧边栏配置with st.sidebar:st.header("算法配置")# 问题选择st.session_state.selected_function = st.selectbox("选择优化问题:",list(TEST_FUNCTIONS.keys()),key="func_select")# 参数配置st.session_state.dimension = st.slider("问题维度:", min_value=10, max_value=100, value=30, step=10)st.session_state.population_size = st.slider("种群大小:", min_value=10, max_value=200, value=50, step=10)st.session_state.max_iter = st.slider("最大迭代次数:", min_value=100, max_value=2000, value=500, step=100)# 仅当函数不是固定边界时才显示边界设置if st.session_state.selected_function not in ["Schwefel", "Rosenbrock"]:col1, col2 = st.columns(2)with col1:st.session_state.lower_bound = st.number_input("搜索下界:", value=-100.0, key="lb_input")with col2:st.session_state.upper_bound = st.number_input("搜索上界:", value=100.0, key="ub_input")st.session_state.save_plot = st.checkbox("自动保存收敛曲线", value=True)# 执行按钮st.markdown("---")if st.button("执行优化算法", key="run_btn", use_container_width=True):run_optimization()# 状态显示if st.session_state.stats:st.markdown("### 最新结果")st.write(f"函数: {st.session_state.stats['function']}")st.write(f"维度: {st.session_state.stats['dimension']}")st.write(f"收敛迭代: {st.session_state.stats.get('convergence_iter', 'N/A')}/{st.session_state.max_iter}")st.write(f"最优适应值: {st.session_state.stats['final_fitness']:.6e}")st.write(f"执行时间: {st.session_state.stats['execution_time']:.2f}秒")# 主显示区域col1, col2 = st.columns([1, 1])with col1:st.header("优化结果")if st.session_state.stats:stats = st.session_state.statsst.subheader("性能统计")st.metric("最终适应值", f"{stats['final_fitness']:.6e}")convergence_info = "未收敛"if stats.get('convergence_iter', -1) > 0:convergence_info = f"{stats['convergence_iter']}/{st.session_state.max_iter}"st.metric("收敛于迭代", convergence_info)st.metric("执行时间", f"{stats['execution_time']:.2f}秒")st.subheader("最优解示例")st.code(f"维度0: {st.session_state.solution[0]:.4f}\n" +f"维度1: {st.session_state.solution[1]:.4f}\n" +f"维度2: {st.session_state.solution[2]:.4f}\n" +(f"...等{stats['dimension']}个维度" if stats['dimension'] > 3 else ""))else:st.info("请配置算法参数并点击'执行优化算法'运行")with col2:st.header("收敛曲线")if st.session_state.convergence_plot:st.pyplot(st.session_state.convergence_plot)if st.session_state.save_plot:buf = io.BytesIO()st.session_state.convergence_plot.savefig(buf, format="png", dpi=150)buf.seek(0)st.download_button(label="下载收敛曲线",data=buf,file_name=f"convergence_{st.session_state.selected_function}_d{st.session_state.dimension}.png",mime="image/png")else:st.image("https://via.placeholder.com/600x400.png?text=等待算法运行...", width=500)# 算法描述st.markdown("---")st.header("算法原理概述")with st.expander("查看蜣螂优化算法细节"):st.markdown("""### 蜣螂优化算法(DBO)蜣螂优化算法根据蜣螂的不同行为划分为4个子种群：1. **滚球蜣螂**：模拟蜣螂滚粪球的直线移动和遇障碍物跳舞重新定位的行为2. **繁殖蜣螂**：模拟将粪球埋入地下，在安全区域繁殖后代的行为3. **小蜣螂**：模拟幼虫长大后的觅食行为4. **偷窃蜣螂**：模拟偷窃其他蜣螂粪球的行为### 改进算法(MSIDBO)本实现包含以下优化策略：- **空间金字塔匹配混沌反向学习初始化**：提高种群多样性和初始解质量- **改进边界收敛因子**：非线性动态调整搜索范围，平衡全局和局部搜索- **融合海鸥优化算法**：加入螺旋攻击机制增强局部开发能力- **t-分布差分变异**：增加算法跳出局部最优能力这些改进策略显著提高了算法的收敛速度和全局优化能力。""")if __name__ == "__main__":main()

http://www.dtcms.com/a/301340.html

相关文章：

  • 【ESP32设备通信】-W5500与ESP32 /ESP32 S3集成
  • MySQL - 性能优化
  • Java面试实战：电商高并发与分布式事务处理
  • maven optional 功能详解
  • Java进阶7：Junit单元测试
  • 数据结构基础内容（第九篇：最短路径）
  • OpenCv中的 KNN 算法实现手写数字的识别
  • 电子电路设计学习
  • git回退版本教程
  • Java validation
  • Java学习第八十部分——Freemarker
  • Linux c网络专栏第三章DPDK
  • Petalinux驱动开发
  • Linux驱动开发笔记（五）——设备树（下）——OF函数
  • 人社部物联网安装调试员的实训平台
  • RabbitMq 常用命令和REST API
  • 9.SpringBoot Web请求参数绑定方法
  • 盛最多水的容器-leetcode
  • 《Java 程序设计》第 7 章 - 继承与多态
  • 记录几个SystemVerilog的语法——时钟块和进程通信
  • maven聚合工程（多个mudule只编译、打包指定module）
  • JVM类加载机制全流程详解
  • 通过硬编码函数地址并转换为函数指针来调用函数
  • Java#包管理器来时的路
  • Leetcode-3427变长子数组求和
  • Mitk教程案例项目编译
  • 嵌入式——单片机的独立按键
  • 【3DsMax+Zbrush+SP】风格化低多边形模型制作教程——以制作杯子为例——03在Substance Painter中制作材质
  • PyTorch深度学习入门记录3
  • 两数之和 II - 输入有序数组-leetcode