Polyhedral Approaches in Combinatorial Optimization组合优化中的多面体方法（下）
目录
1. s-t最短路 多面体表示
2. 生成树与 r-树形图
2.1 生成树多面体
2.2 r-树形图多面体
3. 非二分图匹配
3.1 完美匹配多面体
3.2 匹配多面体 （不一定要覆盖所有顶点）
4. 组合不交
4.1 生成树多面体的整性
4.2 r - 树形图多面体支配集的整性
4.3 极小 k-边连通图的边数上界
1. s-t最短路 多面体表示
尚未找到 （有向图 s-t 经过每个点最多一次）多项式时间内可优化 任意线性函数的多面体描述。
因为最长 s-t路径为NP-hard问题，如果能求解这个问题 就可以在多项式时间内求解哈密顿路径问题（指定起点到终点 经过所有其他点仅一次）
只需对所有的两两顶点 在单位边权下找最长 s−t 路径，并检查是否存在哈密顿路径即可。
正权函数的最短路径问题 s出多1 t进多1 其余进=出
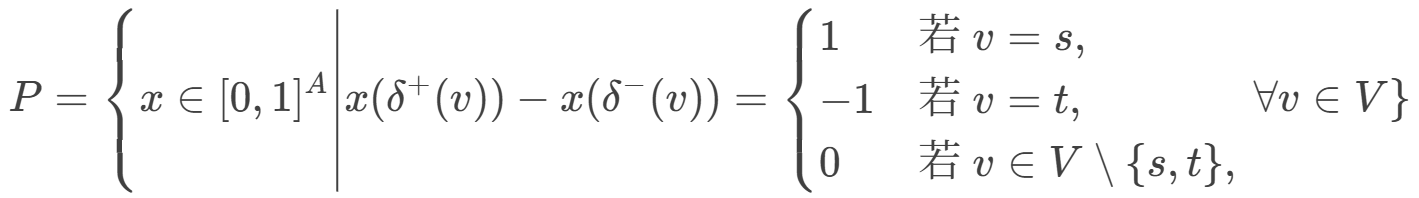
这些整数点 包含一个s-t路径 和若干个环。 下证P的整数性 约束矩阵TU。
x为选边 系数矩阵D为 顶点-弧 关联矩阵（出1 入-1） 右侧b向量
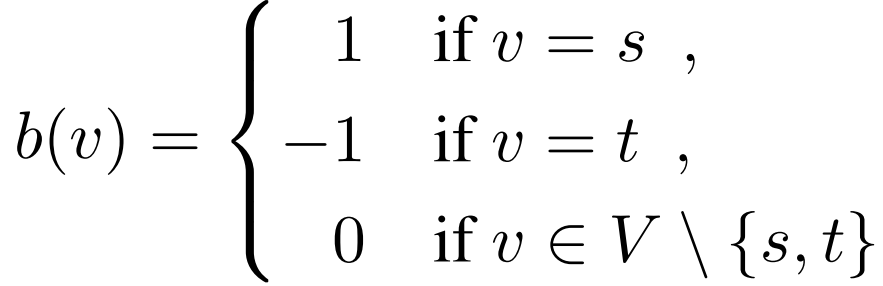
因为每列（每条边）只有 一个1，-1 所以划分行子集的时候
R1取这个子集 和只能为 {0,1,-1} R2取空集即可
2. 生成树与 r-树形图
生成树和树形图（有向版本）对应的组合多面体具有 指数级数量的面。
2.1 生成树多面体
无向图的生成树是满足（1连接所有顶点 2不含环路）的边集 T⊆E：
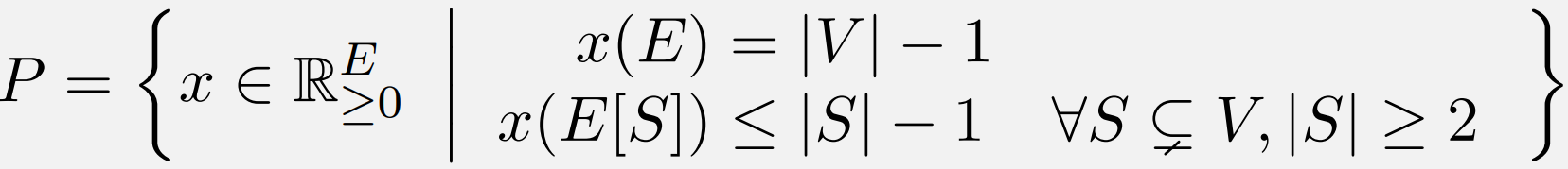
一共选 |V|-1 条边； 任何点集内部连边不能到顶点数（否则就成环）
2.2 r-树形图多面体
有向图中 1忽略方向时为生成树 2从 r 出发可到达任意顶点 / 每个顶点至多一条入弧
引入根r r-树形图多面体的支配锥为：除了r以外 每个子集都会被指向；对应一棵r为根的树形图
3. 非二分图匹配
我们上一次提到 完美二分图匹配； 只需要每个点连边=1的条件 划出了凸包
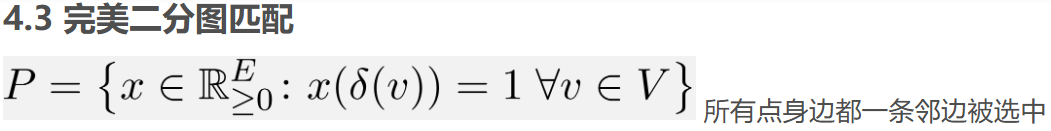
对于普通无向图 要割掉分数极点 形成整凸包还需要加一些边的约束。
3.1 完美匹配多面体
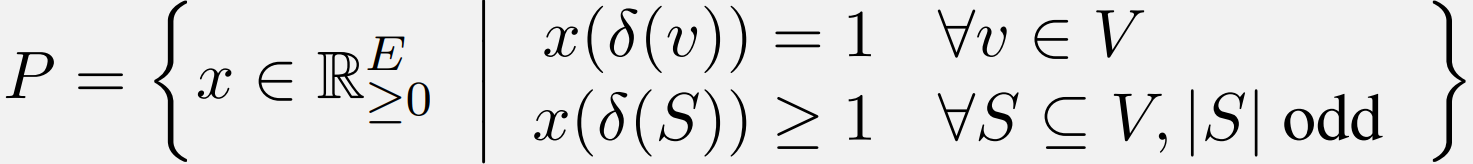
每个点都连一条边； 每个奇数点集都与外界有连边（因为内部无法配对成功 用来去除分数极点）
P的整数点集 与 完美匹配可互相等价。 下证整性：
假设存在使 P 非整数的图 G ，是∣V∣+∣E∣ 最小的反例。 | V |为偶数 否则第二个条件为0
可以发现G的性质：1.是联通的 不然可以仅考虑其包含一条 y - 分形边的一个连通分支
2. y(e)∈(0,1) 因为长度为0的边可以被删去 长度为1的边连接的两点 都没有别的连边了
因为 y(e)∈(0,1) 所以x的≥0的约束是松的 顶点 y 由 ∣E∣ 个线性无关的紧约束唯一确定
紧约束
里面选∣E∣个约束
每个顶点度数至少为2 因为至少要两条分数边才能凑1
所以边数不少于顶点数 |V| ≤ |E| 。 因为y对应|E|个约束 所以 |E| = |W| ≤ |V| 。
左右连接一下 上面都得取等 即为 |V| = |E| = |W| 每个顶点度≥2 顶点数=边数 所以度都为2
所以系统 包含所有点的度数约束，且 G 是一个每个顶点度数恰好为 2 的图
又因为G连通 且顶点数为偶数 则必须是一个包含所有顶点的单偶环
G所对应的 按照边的顺序排列为1-n P的约束就变成了相邻的两条边 y之和 ≥ 1
以n=6 为例 奇数位置的约束 合一起为(e1+e2)+(e3+e4)+(e5+e6) = 3
偶数位置的约束 合一起为 (e2+e3)+(e4+e5)+e6+e1 = 3
奇数行约束之和 = 偶数行约束之和 说明是线性相关 不是满秩的 所以y非极点
|S|>1 因为|V|为偶数 |S|为奇数 所以 |V \ S| > 1 是存在元素的
我们要研究 δ(S) S和V\S 之间的边（这两个大图之间 大图内部的不需要考虑）
可以在图G上 把S缩小成一个超级顶点 剩下的G为G1；把V\S 缩小成一个超级顶点 剩下的G为G2
因为G是最小反例 G1 G2都比G小 所以G1 G2对应的完美匹配多面体都没有分数顶点
我们可以将G1对应的y1和 G2对应的y2 表示为完美匹配的凸组合
三种边：S内部 V\S内部 S与V\S之间；
G1包含V\S内部和 S与V\S之间；G2包含S内部和 S与V\S之间； 所以y1 y2的匹配组合可以表示G
G的y 可以写成y1∪y2 y 是 G 中完美匹配的凸组合 所以不是顶点，所以分数点都不是顶点。
3.2 匹配多面体 （不一定要覆盖所有顶点）
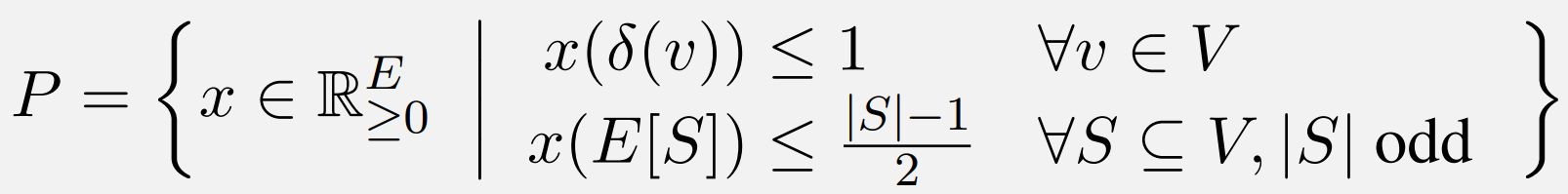
每个点连接不超过1（把 = 变成≤）； 奇数点集内不连半数以上 下证x∈P 都是匹配的凸组合
4. 组合不交
从大的集合族中提取结构良好的集合系统 可帮助证明多面体的整性。
目标为：给定一个 约束数量远多于变量（过度确定）且唯一确定一个点的线性系统，
找到一个结构良好的满秩子系统。 满秩对应唯一确定这个点 结构TU对应整性。
4.1 生成树多面体的整性
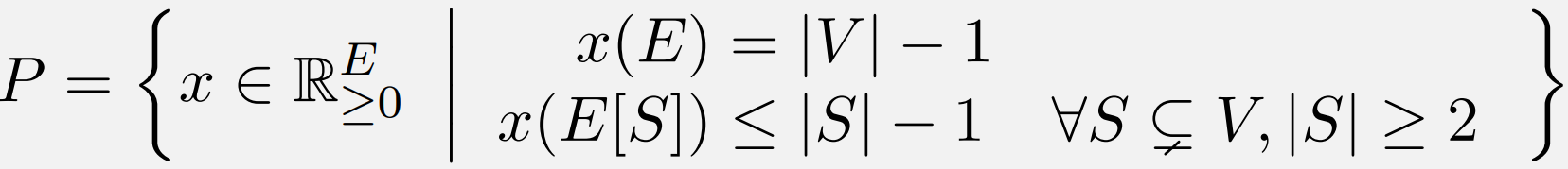
在顶点y上（y中一些边值>0） 对应的紧约束为 =0的哪些边=0约束； ≠0的那些边涉及到的约束
约束数大于变量数。 并且仅考虑紧约束，得到的线性子系统也可能不是全幺模的。
但是，可证明：关于顶点 y 紧 的生成树约束中，总有一个满秩线性子系统是全幺模的。
移除掉y中 对应值为0的边；y在缩减图中仍然为顶点
支撑集supp(y)=E y 中坐标为正的元素对应的边集合
紧集族
证F中的约束 TU
层状族指集合之间要么不相交，要么包含的集合族
(5.13)
因为层状的性质 在这些约束中 S集合的点/边 只会在某几行连续出现
上一讲 连续1矩阵 -> TU 用H内的是TU 推 F中的也是TU
是
的线性组合 (5.14)
由于所有紧生成树约束唯一确定 y，只需证明(5.14)任意紧生成树约束S都可由 (5.13)中的H导出
左边为纯A内 纯B内 A中的点和B中的点 ； 右边为 大集合内+交集内被算了两次
F中的两个顶点子集 如果存在交集 那么不存在只在S1的点 到只在S2的点的边
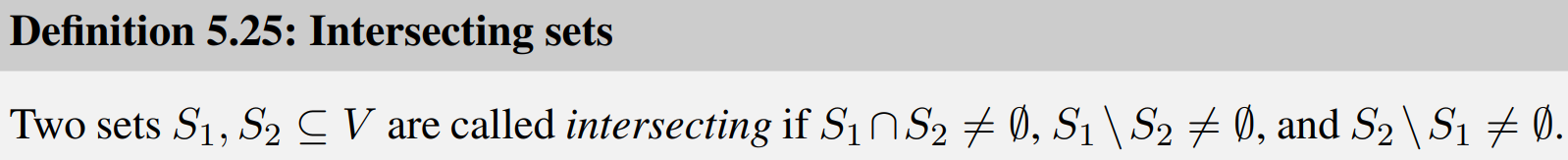
相交集合 这三类点都得存在（否则就会变成相离/包含） laminar层状 即任意两集合都不相交
反证(5.14) 即
Q为H中元素的线性组合
(5.14)不成立等价于 
取S为 所有上面那个冲突中 与H交集元素最少的那个S
交集不为0 否则可以把S加入到H的最高层 而不改变层次性
因为 S∈F H∈F 由引理5.24 
因为等式左侧 前者∉Q 后者∈Q 所以等式右侧两个其中至少有一个∉Q
与S是最小冲突集合矛盾
总的推理过程：
多面体P约束中 能找到全幺模满秩线性子系统 <= 紧集族F中的约束TU <= 极大层状子族中的H TU
4.2 r - 树形图多面体支配集的整性
F为所有y-紧约束的集合
为极大层状子族
正负分组：每个最顶层为+ 下一层为- 再下一层为+ 这样交替
这样的子集嵌套 会让任意一条边 仅在连续的几个子集（连续的几行出现） 所以为TU
有向图类似无向图 只是等式变成 A(S1\S2,S2\S1) + A(S2\S1,S1\S2) 这样双向的
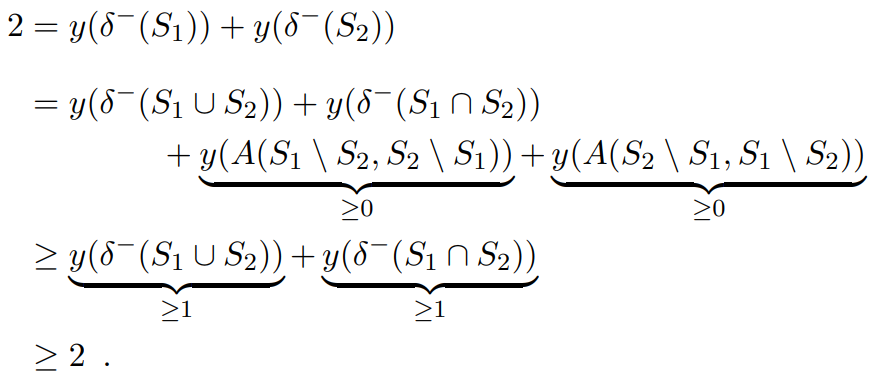
Q为H中元素的线性组合
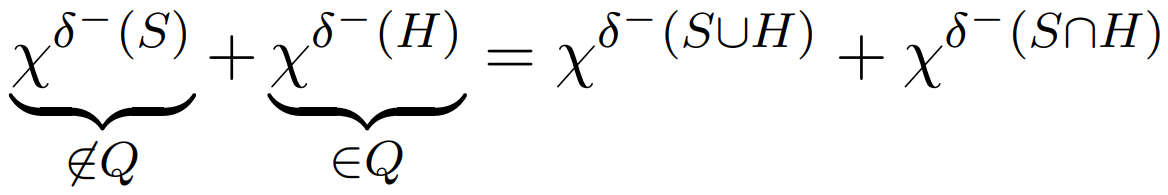与S是最小冲突集合矛盾
H是TU -> 可以在紧约束集F中 找到|A| 个约束构成的满秩子系统为TU -> 对应唯一解且整数解 y
4.3 极小 k-边连通图的边数上界
无向图任意两个顶点间存在 k 条边不交的路径；
即任意两点间最大流≥k；即任意非空真子集的割 ≥ k
构造：1-2-3-n 这样链式的 两两之间都k条边
交叉：相交且 并集≠V
