Mixture-of-Recursions: 混合递归模型，通过学习动态递归深度，以实现对自适应Token级计算的有效适配

PDF: Mixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation

GitHub: Mixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation

---

Abstract

缩放（Scaling）Transformer语言模型取得了令人惊讶的能力，但伴随的计算与内存需求使得训练和部署都极为昂贵。现有的效率优化工作通常只针对参数共享（parameter sharing）或自适应计算（adaptive computation）其中一项，而如何同时实现两者仍是一个开放性问题。

本文引入了Mixture-of-Recursions (MoR)，一个在单个递归Transformer（Recursive Transformer）中统一结合这两种效率维度的框架​​。MoR在递归步（recursion steps）间​​重复使用共享的层堆栈（shared stack of layers）以实现参数效率（parameter efficiency）​​，同时利用一个​​轻量级的token级路由器（token-level router）动态地为tokens分配递归深度（recursion depth）​​，从而​​将计算量呈平方级增长的注意力机制（quadratic attention computation）仅聚焦在最需要的地方​​。

为进一步提升效率，MoR还整合了​​递归层面的键值缓存机制（recursion-wise key-value caching mechanism）​​。该机制通过​​仅为指定tokens有选择地存储键值缓存（selectively storing only the key-value caches for designated tokens）​​，消除了跨递归步的冗余内存访问（redundant memory access）。

在从​​1.35亿（135M）到17亿（1.7B）参数的模型规模上进行预训练实验时，MoR确立了一个新的帕累托边界（Pareto frontier）​​：​​在同等训练FLOPs（浮点运算）条件下，MoR显著降低了验证集困惑度（validation perplexity）并提升了少样本准确率（few-shot accuracy）​​，同时​​相比原始Transformer及现有递归基线模型（vanilla and existing recursive baselines），推理吞吐量（inference throughput）最高提升了2.18倍​​。这些收益表明，MoR是​​在获得大模型（large-model）质量的同时、规避大模型成本的一条有效路径​​。

---

Introduction

研究背景

将Transformer网络扩展到数千亿参数​​，使得网络具备​​强大的少样本泛化与推理能力（few-shot generalization and reasoning abilities）​​。然而，巨大内存占用和计算需求​​，使得在​​超大级数据中心（hyperscale data centers）​​之外进行训练和部署变得​​极其困难​​。这促使研究者们寻找替代性的“高效”设计。在众多效率维度中，​​参数效率以及​​自适应计算​​是当前​​前景广阔且被广泛研究​​的方向。

参数效率（parameter efficiency）：即​​减少或共享模型权重（weights）。实现参数效率的一个​​有效方法​​是​​层权重绑定（layer tying）​​，即在​​多个层（layers）间重复使用同一组共享权重​​。

​​自适应计算（adaptive computation）：即​​仅在需要时才投入更多计算资源​​。对于自适应计算，常见的方法是​​早退机制（early-exiting）​​，该机制​​动态分配计算资源​​：让那些预测​​更简单的token​​更早退出网络​​。

尽管在这两个效率维度上分别取得了进展，但​​仍然缺乏一种能够有效统一参数效率和自适应计算的架构​​。​​

递归Transformer（Recursive Transformers），即​​多次重复应用同一组共享层​​的模型，因其​​内置的权重共享（built-in weight sharing）特性​​，提供了一个​​强大的基础​​。然而，先前在​​动态递归（dynamic recursion）​​方面的尝试常常受到​​实际障碍的限制​​，例如需要​​额外的专门训练流程​​，或面临​​高效部署的挑战​​。这导致大多数方法仍采用更简单的​​固定深度递归（fixed-depth recursion）​​，该方式​​对每个token施加相同量的计算，因而​​无法实现真正自适应的token级计算分配（token-level compute allocation）​​。

本文方法

​​本文提出了混合递归（Mixture-of-Recursions, MoR）框架​​，该框架​​充分挖掘了递归Transformer的潜力（见Figure 1）​​。

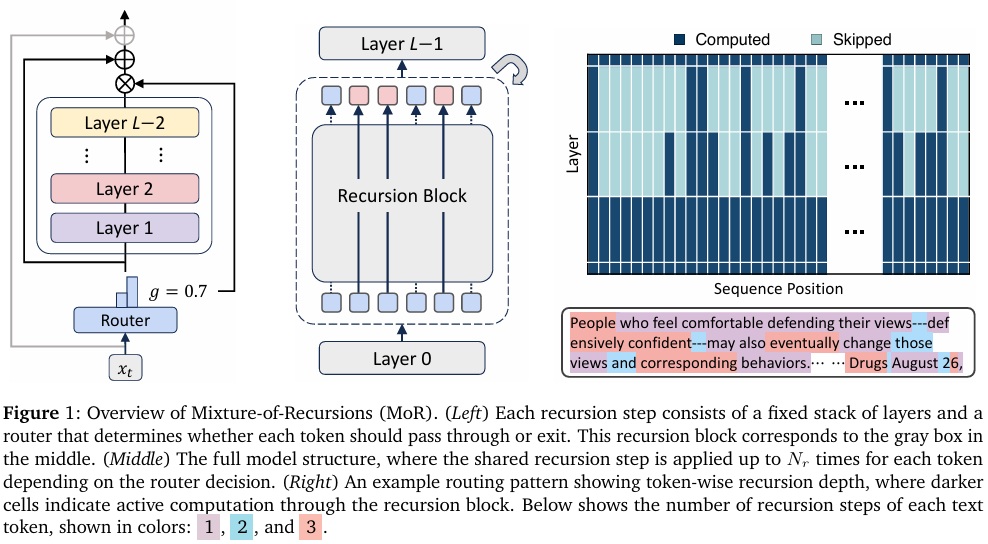
MoR​​端到端（end-to-end）地训练轻量级路由器（routers）​​，为​​每个token分配特定的递归深度（token-specific recursion depths）​​：路由器根据token所需的“思考深度”（depth of “thinking”）​​决定共享参数块（shared parameter block）应作用于该token的次数​​，从而​​将计算资源精准导向最需要的地方​​。

这种​​动态的token级递归（token-level recursion）​​天然支持​​递归层面的键值缓存（recursion-wise key–value (KV) caching）​​，即​​有选择地存储和检索与每个token实际分配到的递归深度相对应的键值对（key–value pairs）​​。

这种​​目标导向的缓存策略（targeted caching strategy）​​ ​​显著减少了内存流量（reduces memory traffic）​​，从而​​在不依赖后期（post-hoc）修改的情况下提升了吞吐量​​。

因此，MoR在单一架构内​​同时实现了三重效率提升​​：(i) ​​权重绑定以减少参数​​，(ii) ​​路由token以减少冗余浮点运算（redundant FLOPs）​​，以及 (iii) ​​递归式缓存键值以减少内存流量​​。

从概念上讲，MoR提供了一个​​用于隐空间思考（latent space reasoning）的预训练框架​​——通过​​迭代应用单个参数块来执行​​非语言式的思考（non-verbal thinking）​​。然而，与那些在生成前对​​增强的连续提示（augmented continuous prompts）​​进行深思熟虑（deliberate）的方法不同，MoR​​直接在解码每个​​token的过程中实现这种隐空间思考（latent thinking）​​。

此外，其​​路由机制（routing mechanism）​​促进了模型​​纵向（沿深度轴 depth axis）的自适应推理（adaptive reasoning）​​（这种思考沿深度轴进行，类似于在序列水平轴 horizontal sequence axis 上生成连续想法），​​超越了先前工作中常见的统一、固定思考深度（uniform, fixed thinking depth）​​。​

​本质上，MoR使模型能够根据每个token的需求高效调整其思考深度，从而将参数效率与自适应计算统一起来​​。

本文贡献​

• ​​统一的语言建模高效框架​​：本文提出了​​混合递归（Mixture-of-Recursions, MoR）​​，这是首个​​在单一框架内统一多种效率范式​​的架构——​​参数共享​​、token级自适应思考深度​​和​​内存高效的键值缓存​​。
• ​​动态递归路由​​：本文引入了​​一个从头开始训练（trained from scratch）的路由​​，用于​​分配动态的token级递归深度（dynamic per-token recursion depths）​​。这​​确保了训练与推理行为的一致性（aligns training with inference-time behavior）​​，并​​消除了传统早退方法中所需的、成本高昂且损害性能的后置路由阶段（post-hoc routing stages）​​。
• ​​广泛的实证验证​​：在​​同等计算预算（equal compute budgets）​​下，针对​​从1.35亿到17亿参数（此为基模型大小，MoR模型因参数共享拥有更少的唯一参数）的模型范围​​进行实验，结果表明：MoR通过​​改进验证损失（validation loss）和少样本准确率（few-shot accuracy）​​，相对于​​原始Transformer和递归基线模型（vanilla and recursive baselines）​​，​​建立了一个新的帕累托边界（Pareto frontier ）​​。
• ​​高效架构​​：MoR​​通过有选择地仅让必需序列参与注意力运算（selectively engaging only essential sequences in attention operations）​​，​​显著降低了训练FLOPs​​。同时，​​键值缓存大小的减少（reduction in KV cache sizes）​​带来了​​推理吞吐量本身的提升（enhanced inference throughput itself）​​，而​​持续的深度级批量处理（continuous depth-wise batching）​​又进一步​​放大了这一提升效果。

---

Method​

1. 预备知识 (Preliminary)​​

​​递归Transformer (Recursive Transformers)​

标准Transformer (Vaswani et al., 2017) 通过堆叠 L 个唯一的层来构建token表示 (token representations)，每个层包含一个自注意力机制 (self-attention) 和一个前馈网络 (feed-forward network)。在时间步 t，隐藏状态 (hidden state) htl​ 的演化过程为：

其中， 表示第  层的参数。​​

递归Transformer旨在通过跨深度重用层来减少参数量。它们不再拥有 L 组不同的权重，而是将模型划分为 Nr​ 个递归块 (recursion blocks)，每个块使用共享的参数池 Φ′。这种设计允许增加计算量（通过增加有效网络深度）而不增加参数量。

​​参数共享策略 (Parameter-sharing strategies)​

本文研究了四种参数共享策略：循环 (Cycle)、序列 (Sequence)，以及它们的变体​​中周期 (Middle-Cycle)​​ 和​​中序列 (Middle-Sequence)​​。表1总结了两种主要设计，完整列表在附录的表5中给出。

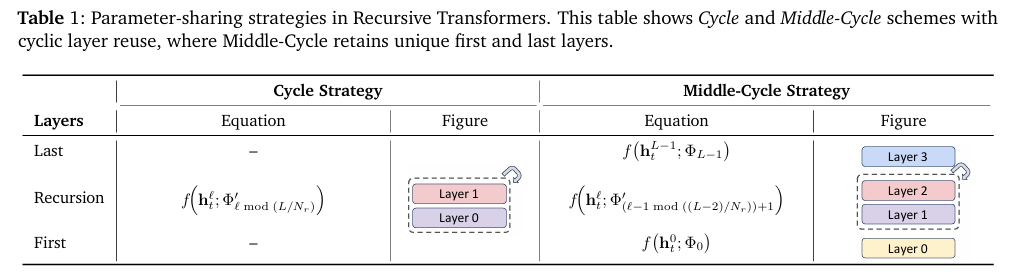
在​​循环共享中，递归块被循环重用。例如，考虑一个原始的非递归模型有 L=9 层，其递归对应版本使用 Nr​=3 次递归。在“循环”策略下，层被共享并展开为 [(0,1,2) (0,1,2) (0,1,2)]。在​​序列 共享中，每个递归块在移动到下一个块之前连续重用相同的层，对于相同的配置会导致 [(0,0,0) (1,1,1) (2,2,2)]。两者在展开时具有相同的有效层数 (L=9)，但顺序不同。此外，​​“中”(Middle)​​ 变体保留首层和末层 (和) 的完整容量参数 (full-capacity parameters)，而在中间层之间共享权重。

​​递归模型中增强的训练和推理效率 (Enhanced training and inference efficiency in recursive models)​

参数共享策略可以将唯一可训练参数的数量减少为递归次数的因子，从而有效分摊模型的内存占用。从分布式训练的角度来看，在使用​​全分片数据并行 (Fully Sharded Data Parallel, FSDP)​​ (Zhao et al., 2023) 时，这变得非常高效。

虽然单个 ​​all-gather​​ 操作以前只支持一次迭代（即 1 次迭代/收集），但递归模型在所有递归步骤中重用相同的已收集参数（即 Nr​ 次迭代/收集）。

此外，​​递归架构支持一种新颖的推理范式——连续深度级批处理 (continuous depth-wise batching)。该技术允许处于不同阶段的token被分组到单个批次中，因为它们都使用相同的参数块。这可以消除​​气泡 (bubbles)​​——即等待其他样本完成所花费的空闲时间——从而带来显著的吞吐量提升。

​​先前工作的局限性 (Limitations in prior works)

尽管模型参数被绑定 (tied)，但​​通常为每个深度使用不同的键值缓存 (KV caches)​​。这种设计未能减少缓存大小，意味着高检索延迟 (retrieval latency) 仍然是一个严重的推理瓶颈。

此外，大多数现有的递归模型只是对​​所有token应用固定的递归深度 (fixed recursion depth)​​，忽略了其变化的复杂性。虽然像早退机制 (early-exiting methods) 这样的后处理 (post-hoc) 方法可以引入一些自适应性 (adaptivity)，但它们通常需要​​单独的训练阶段 (separate training phases)​​，这可能会降低性能 。

理想情况下，递归深度应该在预训练期间​​动态学习 (learned dynamically)​​，使模型能够以数据驱动的方式适应每个token的难度来调整其计算路径。然而，这样的动态路径引入了一个新挑战：退出的token在后续递归深度上将缺少键值对 (KV pairs)。

解决这个问题需要一种​​并行解码机制 (parallel decoding mechanism)​​来高效计算实际的键值对，但这需要单独且复杂的工程，并使系统复杂化。

2. 混合递归 (Mixture-of-Recursions)​​

本文提出 ​​混合递归 (Mixture-of-Recursions, MoR)​​ ——一个在预训练和推理期间​​动态调整每个token的递归步骤 (dynamically adjusts recursion step for each token)​​ 的框架。MoR 的核心在于两个组件：一个​​路由机制，它分配token特定的递归步骤以自适应地将计算集中在更具挑战性的token上；以及一个 ​​KV 缓存策略 (KV caching strategy)​​，它定义了键值对如何存储并在每个递归步骤中​​有选择地用于注意力机制 (selectively utilized for attention)​​。

2.1 路由策略：专家选择 vs. token选择 (Routing Strategies: Expert-choice vs. Token-choice)​​

​​专家选择路由 (Expert-choice routing)

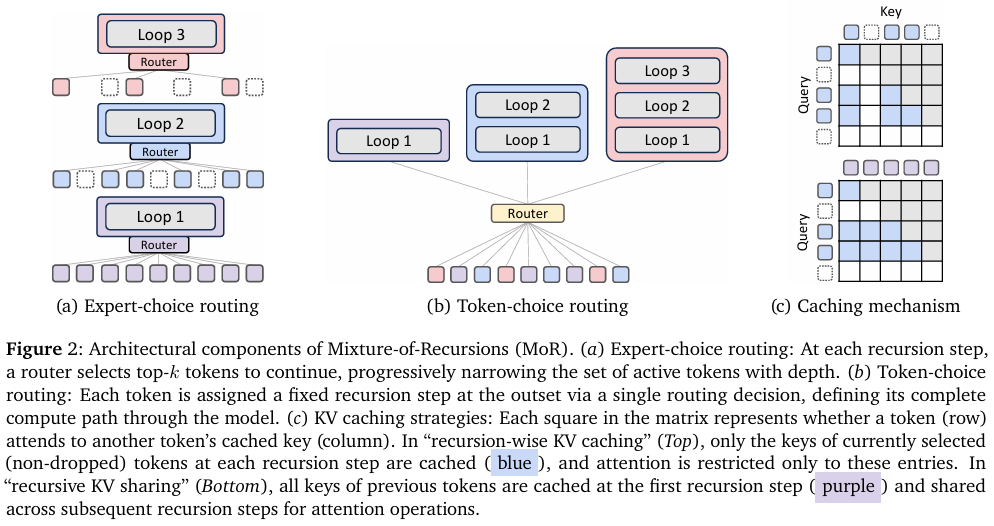
(图 2a) 受 ​​MoD (Mixture-of-Depths)​​ 模型 (Raposo et al., 2024) 中 ​​top-k门控机制 (top-k gating)​​ 的启发，在专家选择路由中，每个递归深度成为一个​​专家并选择其偏好的 top-k 个token（例如，对于 Nr​=3，本文有三个专家：专家1应用第一次递归步骤，专家2应用第二次递归步骤，依此类推）。在每个递归步骤 r，相应的​​路由使用隐藏状态（输入到第 r 个递归块的隐藏状态）及其路由参数 θr​ 来计算token t 的标量分数 。这里，G 表示一个激活函数，如 ​​sigmoid​​ 或 ​​tanh​​。然后，选择 top-k 个token通过递归块：

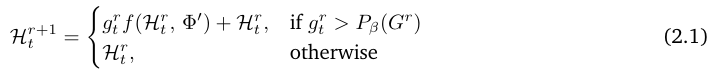
其中是递归步骤 r 上所有分数的 τ-百分位阈值 (τ-percentile threshold)。

为了确保步骤间的连贯推进，本文采用​​分层过滤 (hierarchical filtering)​​：只有在递归步骤 r 被选中的token才能在步骤 r+1 被重新评估。

这模拟了早退行为 (early-exit behavior)，同时是从头开始学习的。随着更深的层倾向于编码越来越抽象和稀疏的信息 ，​​该机制优先计算仅针对需求最高的tokens (prioritizes computation for only the most demanding tokens)​​。

Token选择路由（Token-choice routing）

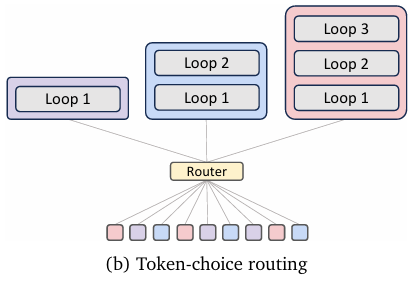
（图 2b）与​​专家选择（expert-choice）​​（在每一步递归中筛选token）不同，​​token选择（token-choice）​​ ​​从一开始就将每个token分配给完整的递归块序列（commits each token to a full sequence of recursion blocks from the start）​​。形式化地说，给定隐藏状态（在​​中周期策略（Middle-Cycle strategy）​​下，​），​​路由​​ 对​​专家执行​​非线性函数（non-linear function）​​（softmax 或 sigmoid）：

其中表示专家 j∈{1,…,Nr​} 的​​路由分数（routing score）​。t

Token被分配给专家（​​Top-1门控（top-1 gating）​​），这对应于​​顺序应用递归 i 次（sequentially applying the recursion i times）​​。随后，隐藏状态按以下方式递归更新：

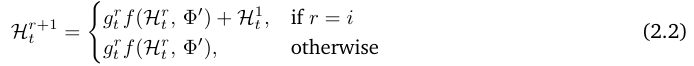
​​为在同等计算量下比较路由策略​​，本文将​​专家选择​​ 的​​token分配预算（token allocation budgets）​​ 与​​token选择​​对齐。

具体而言，本文校准（calibrate）​​专家选择的​​token容量（token capacity）​​（即 top-k），以匹配​​完美负载均衡（perfect load balancing）​​的token选择路由的期望token分布。在完美均衡的token选择中，每个token以​​等概率 1/Nr​​​ 被分配到递归深度 i∈{1,…,Nr​}。因此，​​递归步骤 j 处理的token比例（fraction）​​为 (Nr​−j+1)/Nr​。例如，当 Nr​=3 时，递归步骤 1、2、3 分别处理 {3/3,2/3,1/3} 的token。相应地，本文在专家选择的 top-k 筛选中应用​​相同的比例分配（fractional allocation）​​（即 k 按序列 Nr​/Nr​,…,1/Nr​ 在 Nr​ 个递归步骤中分配）。

​​优势与局限（Strengths and limitations）

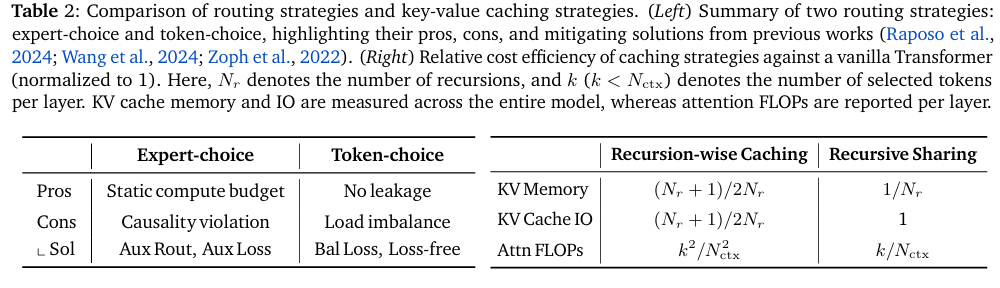
（表 2-左）尽管专家选择路由通过​​静态 top-k 筛选（static top-k selection）​​ 保证了​​完美负载均衡（perfect load balancing）​​，但它存在​​信息泄露（information leakage）​​问题。这种训练期间的​​因果性违背（violation of causality）​​迫使本文采用​​辅助路由器（auxiliary router）​​或​​正则化损失（regularization loss），旨在推理时​​精确检测 top-k tokens（detect top-k tokens）​​而无需访问未来token信息。

与此同时，token选择（token-choice）​​虽无此类泄露问题，但由于其​​固有的负载均衡挑战（inherent load balancing challenges）​​，通常需要​​平衡损失（balancing loss）​​或​​无损失算法（loss-free algorithms）。

2..2 KV 缓存策略：递归式缓存 vs. 递归共享​​

​​动态深度模型（Dynamic-depth models）​​在​​自回归解码（autoregressive decoding）​​期间常面临 ​​KV 缓存一致性（KV cache consistency）​​问题。当一个token​​提前退出（exits early）​​时，其在更深层的对应​​键和值（keys and values）​​将缺失，而这可能对后续token至关重要。现有方法尝试​​复用陈旧条目（reuse stale entries）​​或运行​​并行解码（parallel decoding）​​，但这些方案仍会引入​​额外开销（overhead）​​和​​复杂性（complexity）​​。为此，本文设计并探索了两种专为 MoR 模型定制的 KV 缓存策略：​​递归式缓存（recursion-wise caching）​​与​​递归共享（recursive sharing）​​。

​​递归式 KV 缓存（Recursion-wise KV caching）

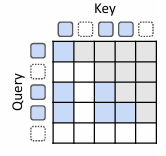
（图 2c-上）本文​​有选择地缓存键值对（cache KV pairs selectively）​​：​​仅被路由到特定递归步骤的tokens（only tokens routed to a given recursion step）​​在该层级存储其​​键值条目（key–value entries）​​。因此，​​每个递归深度的 KV 缓存大小（KV cache size）​​ 由专家选择中的​​容量因子（capacity factor）​​精确决定，或根据token选择中的​​实际均衡比例（actual balancing ratios）​​确定。​​

注意力计算（Attention）​​随后被限制在这些​​本地缓存的tokens（locally cached tokens）​​上。这一设计​​促进了块本地计算（promotes block-local computation）​​，提升了​​内存效率（memory efficiency）​​并减少了 ​​I/O 需求（IO demands）​​。

​​递归 KV 共享（Recursive KV sharing）

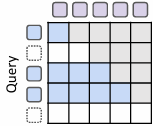
（图 2c-下）MoR 模型的​​关键设计选择（key design choice）​​是：​​所有tokens至少经过第一个递归块（all tokens traverse at least the first recursion block）​。利用这一点，​​仅在初始步骤（exclusively at this initial step）​​缓存 KV 对，并在所有后续递归中​​复用（reusing）​​它们。因此，​​查询长度（query length）​​可能随递归深度增加而缩短（基于​​选择容量（selection capacity）​​），但​​键和值长度（key and value lengths）​​将始终​​保持完整序列（consistently maintain the full sequence）​​。这确保了​​所有tokens无需重新计算即可访问历史上下文（all tokens can access to past context without recomputation）​​，尽管存在​​分布不匹配（distribution mismatch）​​。

​​优势与局限（Strengths and limitations）

（表 2-右）​​递归式缓存（Recursion-wise caching）​​将整个模型的 ​​KV 内存和 I/O（KV memory and IO）​​ 削减至约 (Nr​+1)/(2Nr​) 倍（假设容量因子遵循序列 Nr​/Nr​,…,1/Nr​ 分布）。它还将​​每层注意力 FLOPs（per-layer attention FLOPs）​​ 降至普通模型（vanilla models）的 倍（其中 Nctx​ 为​​上下文长度（context length）​​），从而​​显著提升训练和推理阶段的效率（substantially improved efficiency）​​。与此同时，​​递归共享（recursive sharing）​​通过​​全局复用上下文（globally reusing context）​​可实现​​最大内存节省（maximal memory savings）​。具体而言，​​跳过共享深度的 KV 投影和预填充操作（skipping KV projection and prefill operations）​​可带来显著的加速。然而，​​注意力 FLOPs（attention FLOPs）​​仅按因子减少，且​​大量的 KV I/O（high volume of KV IO）​​仍会导致​​解码瓶颈（decoding bottleneck）​​。

---

Experiments​

在基于 ​​Llama 的 Transformer 架构 (Llama-based Transformer architecture)​​上，参考 ​​SmolLM 开源模型 (SmolLM open-source models)​​ 的配置，使用 ​​SmolLM-Corpus​​中的 ​​FineWeb-Edu 数据集​​ 的去重子集​​从头开始预训练（pretrain from scratch）​​本文的模型。本文在 ​​FineWeb-edu​​ 的验证集和​​六个少样本评测基准（six few-shot benchmarks）​​ 上评估模型。

1. 主要结果 (Main Results)​​

​​MoR 在参数量更少的情况下以同等训练计算量超越基线模型 (MoR outperforms baselines with fewer parameters under equal train compute)​

在 ​​16.5e18 FLOPs​​ 的同等训练计算预算下，本文的​​混合递归 (Mixture-of-Recursions, MoR)​​ 模型与​​普通 Transformer (Vanilla Transformer)​​ 和​​递归 Transformer进行了比较。

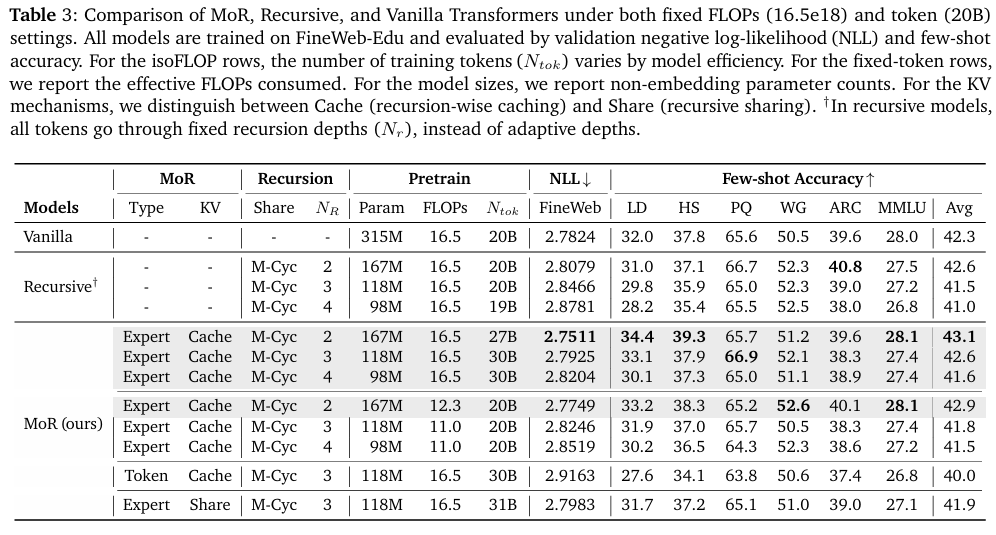
如表 3 所示，使用​​专家选择路由器 (expert-choice router)​​ 和​​两次递归 (two recursions)​​ 的 MoR 模型取得了​​更低的验证损失 (lower validation loss)​​，并在​​平均少样本准确率 (average few-shot accuracy)​​ 上超过了普通基线模型 (43.1% vs. 42.3%)。

值得注意的是，尽管使用了几乎​​少 50% 的参数 (using nearly 50% fewer parameters)​​，却实现了这种卓越的性能。这归因于 MoR ​​更高的计算效率 (higher computational efficiency)​​，使其能够在相同的 FLOPs 预算下​​处理更多的训练tokens（process more training tokens）​​。

此外，当 Nr​ 增加到 3 或 4 时，​​MoR 保持了其有竞争力的准确率 (maintains its competitive accuracy)​​，持续优于递归基线模型，同时与​​全容量 (full-capacity)​​ 普通模型的差距保持在很小范围内。

​​MoR 在同等数据量下以更少的计算量超越基线模型 (MoR outperforms baselines with less compute at equal data)​

为了分离架构差异，本文分析了在​​固定数量的训练tokens（20B） (fixed number of training tokens (20B))​​ 下的性能。具体而言，本文的 Nr​=2 的 MoR 模型优于普通和递归基线模型——实现了更低的验证损失和更高的准确率——尽管​​训练 FLOPs 减少了 25% (using 25% fewer training FLOPs)​​。

这种​​理论效率（theoretical efficiency）转化为显著的实践收益（significant practical gains）​​：与普通基线模型相比，本文的模型​​减少了 19% 的训练时间（reduces training time by 19%）​​并​​降低了 25% 的峰值内存使用量（cuts peak memory usage by 25%）​​。

这些改进源于本文的​​分层过滤 (hierarchical filtering)​​ 和​​递归层注意力机制 (recursion-wise attention mechanism)​​，它们通过​​缩短序列长度（shorten sequence lengths）​​实现了更优的​​计算-准确率权衡（compute-accuracy trade-off）​​，即使在预训练期间也是如此。

​​MoR 的性能因路由和缓存策略而异 (MoR performance varies with routing and caching strategies)​

本文也在 MoR 框架内评估了几种设计变体，特别是在 Nr​=3（这是轻量级且仍可与普通模型媲美的配置）的情况下。在此情况下，使用token选择路由（token-choice routing）​​比使用​​专家选择路由​​ 的性能更低（40.0% vs. 42.6%），​​表明路由的粒度（routing granularity）对模型性能起着关键作用（plays a pivotal role）​​。

此外，应用 ​​KV 缓存共享（KV cache sharing）​​相比​​独立缓存（independent caching）​​略微降低了性能，但同时提供了​​更高的内存效率（improved memory efficiency）​​。当内存使用是关键考量因素时，这种权衡在实际部署中仍然是​​有利的（favorable）​​。

2. 等计算量分析 (IsoFLOP Analysis)​​

评估新模型架构设计的​​一个核心标准（core criterion）​​是​​性能能否随着模型和计算规模的增长而持续提升（whether performance continues to improve as model and compute scales grow）​​ (Kaplan et al., 2020)。因此，本文在广泛的模型规模和计算预算范围内评估 MoR 与普通及递归 Transformer，以证明其在规模增加时​​保持竞争力或更优的预测性能（maintains competitive or superior predictive performance）​​。

​​实验设置 (Experimental Setup)​

在​​四个规模（four scales）​​上进行了实验——​​1.35亿（135M）、3.6亿（360M）、7.3亿（730M）和 17亿（1.7B）参数​​——将递归模型和 MoR 配置的递归次数固定为三（Nr​=3），导致​​唯一参数量大约仅为普通模型的三分之一（roughly one-third the number of unique parameters）。每个模型在三个 FLOPs 预算下进行预训练：​​2e18、5e18 和 16.5e18​​。

​​MoR 是一种可扩展且参数高效的架构 (MoR is a scalable and parameter-efficient architecture)

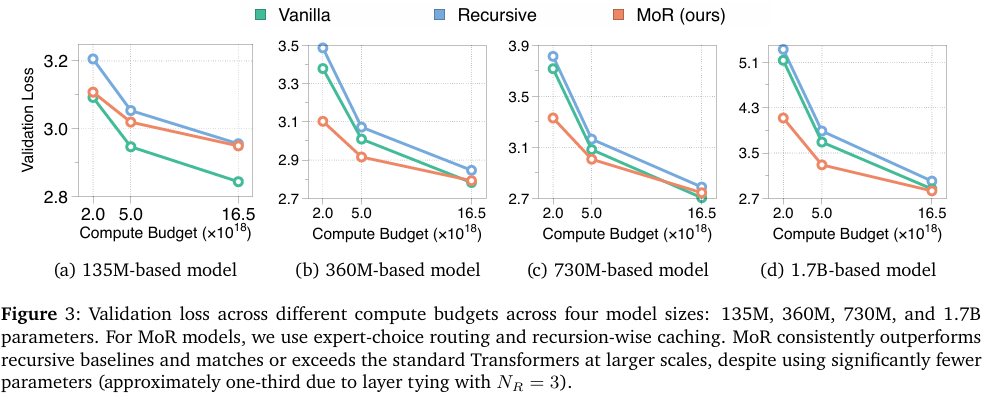
如图 3 所示，在所有模型规模和计算预算下，MoR ​​持续优于（consistently outperforms）​​递归基线模型。虽然在最小模型规模（135M）下其表现略逊于普通模型——可能是由于​​递归容量瓶颈（recursive capacity bottleneck）​​所致——但随着规模扩大，这种差距迅速缩小。对于 ​​>3.6亿参数 (>360M parameters)​​ 的模型，​​MoR 不仅能匹配（matches）​​普通 Transformer，​​通常还能超越（exceeds）​​它，尤其是在​​低到中等（low- and mid-range）​​预算下。

总体而言，这些结果突显了 MoR 是标准 Transformer 的一种​​可扩展且高效的替代方案（scalable and efficient alternative）​​。它以​​显著降低的参数量（significantly lower parameter counts）​​实现了强大的验证性能，使其成为​​预训练和大规模部署（pretraining and large-scale deployment）​​的有力候选者。

3. 推理吞吐量评估 (Inference Throughput Evaluation)​​

作为​​参数共享架构 (parameter-shared architecture)​​，MoR 能够利用​​连续深度级批量处理 (continuous depth-wise batching)​​ ，与普通 Transformer 相比​​显著提升推理吞吐量 (dramatically boost inference throughput)​​。该技术通过在解码过程中​​立即用新到达的token替换已完成的序列（immediately replacing completed sequences with incoming tokens）​​ 来保持​​高且一致的 GPU 利用率（high and consistent GPU utilization）​​。MoR 中的​​早退机制（early-exiting mechanism）​​进一步​​消除了计算批次中的气泡（eliminates bubbles in the computational batch）​​。

​​实验设置 (Experimental Setup)

本文测量了基于 ​​3.6亿（360M）参数规模​​、在 ​​16.5e18 FLOPs​​ 预算下训练的 MoR 模型的吞吐量，其​​递归深度（recursion depths）​​ 分别为 2、3 和 4。​​吞吐量（Throughput，tokens/second）​​ 基于​​每个样本生成token的时间（generation time for tokens per sample）​​ 来测量，其中token数量采样自​​均值为 256​​ 的正态分布，且​​不包含任何输入前缀（starting without any input prefix）​​。

本文考察两种​​批次配置（batching configurations）​​：​​固定批次大小（fixed batch size）为 32​​，以及一个​​（相对）最大批次大小（(relative) maximum batch size）​​（通过将 32 乘以普通模型与 MoR 模型的​​最大批次大小比值（ratio of the maximum batch sizes）​​ 得到）。实验设置的更多细节见附录 D。

​​MoR 通过连续深度级批量处理提升推理吞吐量 (MoR boosts inference throughput with continuous depth-wise batching)

​

如图 4a 所示，在两种批次设置下，​​所有 MoR 变体都优于普通基线模型（vanilla baseline）​​，即使后者也利用了​​连续序列级批量处理（continuous sequence-wise batching）​​ 。

​​增加递归深度（Increasing recursion depth）​​会导致​​更多token提前退出（leads to more tokens exiting early）​​ 以及 ​​KV 缓存使用量进一步减少（further reduction in KV cache usage）​​。

这反过来又​​显著提高了吞吐量（boosts throughput significantly）​​（例如，当 ​​B = Max​​ 时，​​MoR-4 实现了最高 2.06 倍的加速（up to a 2.06× speedup）​​）。虽然性能略有下降（performance degradation），但考虑到​​吞吐量的显著提升（substantial throughput gain）​​，这​​可以是一个有利的权衡（can be a favorable trade-off）​​。

这些结果证实了将​​深度级批量处理范式（depth-wise batching paradigm）​​ 与​​早退机制（early-exiting）​​ 相结合，能​​显著加速 MoR 的实际部署吞吐量（significantly accelerate MoR’s actual deployment throughput）​​。

Ablation Studies​

1. 参数共享策略 (Parameter Sharing Strategies)​​

​​中周期是最有效的参数共享策略 (Middle-Cycle is the most effective parameter sharing strategy)​

​​参数共享 是递归 Transformer 和 MoR 的关键组成部分。为了确定​​最有效的共享配置（most effective sharing configuration）​​，本文通过实验比较了前述四种策略：​​循环、序列、中周期​​ 和 ​​中序列​​。本文在基于 ​​1.35亿（135M）​​ 和 ​​3.6亿（360M）参数规模​​ 的递归 Transformer 上评估了每种策略。

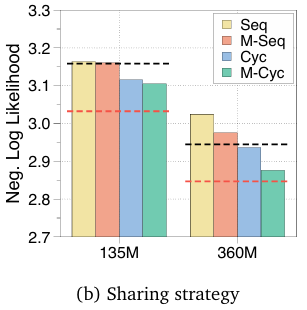
如图 4b 所示，“​​中周期（Middle-Cycle）​​”策略​​始终实现最低的验证损失（consistently achieves the lowest validation loss）​​，其优越性在附录 E 的详细结果中得到进一步证实。基于这些发现，本文后续展示的所有 MoR 和递归 Transformer 中均​​采用（adopt）​​ “​​中周期（Middle-Cycle）​​”配置。

​​4.2. 路由策略 (Routing Strategies)​​

本文对 MoR 框架中​​专家选择​​和 ​​token选择路由方案的各种设计选择的影响进行了​​广泛的消融研究（extensive ablation study）​​。

​​在专家选择路由中，辅助损失和线性路由器提供最佳性能 (In expert-choice routing, auxiliary loss and linear router yield the best performance)

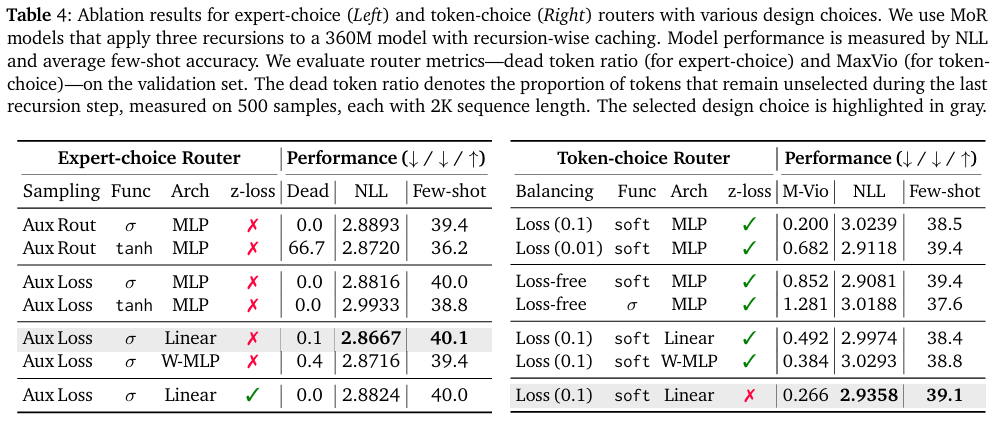
对于专家选择路由设置（表 4 左），本文评估了多个设计方面：​​缓解因果性违背（mitigate causality violation）的解决方案​​（​​辅助路由器（auxiliary router） vs 辅助损失（auxiliary loss）​​）、​​标准化函数（normalization functions）​​（​​sigmoid vs tanh​​）、​​路由器架构（router architectures）​​（​​MLP（多层感知机）、Linear（线性）、或 Wide-MLP（宽MLP）​​）以及​​辅助 z 损失（auxiliary z-loss）​​ 的影响。

为了评估路由器执行​​动态分配（dynamic allocation）​​的能力，本文测量了在验证数据集上“​​死tokens（dead tokens）​​”——即在批次中​​从未被最后一个递归选中的token（those never selected by the final recursion）​​——的比例。本文的主要发现如下：

首先，​​使用辅助损失（auxiliary loss）​​ 对于​​推理时行为（inference-time behavior）​​ 比​​训练一个独立的辅助路由器（training a separate auxiliary router）​​ 更有效。

其次，​​sigmoid 标准化函数（sigmoid normalization function）​​ 和​​简单的线性路由器架构（simple linear router architecture）​​ 带来最佳性能。

最后，​​辅助 z 损失（auxiliary z-loss）​​ 对准确率的影响​​可以忽略不计（negligible impact）​​，尽管它确实略微​​降低了死token比例（reduces the proportion of dead tokens）​​。

​​在token选择路由中，平衡损失实现稳定准确的路由 (In token-choice routing, balancing loss yields stable and accurate routing)

对于token选择路由（表 4 右），本文遵循 ​​MoE（混合专家，Mixture-of-Experts）​​ 的常见做法，​​默认启用 z 损失（enable z-loss by default）​​。

本文比较了两种​​平衡策略（balancing strategies）​​：​​使用平衡损失（using a balancing loss）​​ 和​​使用路由器偏置以无损失的方式进行训练（training in a loss-free manner using router bias）​​。虽然两种方法在​​对数概率（log-probability）​​ 和​​少样本准确率（few-shot accuracy）​​ 上表现相似，但​​显式平衡损失（explicit balancing loss）​​ 在 MoR 架构中显著降低了 ​​MaxVio（最大违规值），使其成为​​更可取的（preferable）稳定路由选择（stabler routing）​​。

然而，尽管如此，即使在近一半的训练步骤中，模型也经常难以在​​异构专家（heterogeneous experts）​​ 之间平衡负载。​​采用 MLP 路由器的 Softmax 激活（Softmax activation with an MLP router）​​ 表现最好，而​​移除 z 损失（removing z-loss）​​——尽管在最终设计中以非常小的系数重新添加回来——​​反而带来更高的性能和路由稳定性（results in higher performance and routing stability）​​。

3. KV 缓存策略 (KV Caching Strategies)​​

​​即使在参数共享架构中，KV 共享也能稳健工作 (KV sharing robustly works even in parameter-shared architectures)​

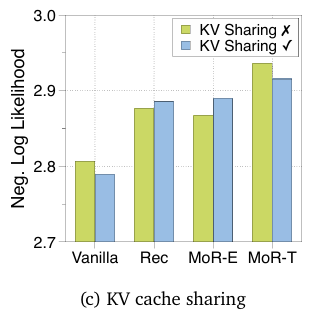
在图 4c 中，本文首先研究了​​KV 共享在普通 Transformer 和递归 Transformer 中的影响。与​​先前工作（prior works） 一致的是，如果模型​​从头开始预训练（pretrain from scratch）​​，由于​​更大的参数灵活性（greater parameter flexibility）​​，​​KV 共享通常不会损害性能（does not often compromise performance）​​。

令人惊讶的是，​​递归 Transformer（Recursive Transformer）​​ 尽管其​​自由度减少（reduced degrees of freedom）​​，对 KV 共享却保持了相对稳健。本文通过将每个递归深度的 KV 对​​分解（decomposing）​​ 为​​幅值（magnitude）​​ 和​​方向（direction）​​ 找到了支持这一点的证据。

​共享参数（share parameters）​​ 的深度之间表现出​​高度一致的幅值模式（highly consistent magnitude patterns）​​ 和​​高余弦相似度（high cosine similarity）​​，这为​​KV 共享仅导致轻微性能下降（KV sharing results in only a slight performance drop）​​ 提供了明确的理由。

​​KV共享会损害专家选择路由，但有益于MoR中的token选择路由 (KV sharing degrades expert-choice but benefits token-choice routing in MoR)

本文在 MoR 框架中比较了​​递归式 KV 缓存（recursion-wise KV caching）​​ 和 ​​递归 KV 共享（recursive KV sharing）​​ 机制。本文观察到，虽然​​递归 KV 共享​​具有​​减少内存占用（reduced memory footprint）​​ 和 ​​总计算量减少（overall FLOPs）​​的优势，但它在​​固定token数（fixed token）​​ 设置下会导致​​专家选择路由​​ 的性能​​大幅下降（quite large performance degradation）​​。这表明​​仅更新和关注在该递归深度活跃的token（exclusively updating and attending to the tokens active in that recursion depth）​​ 可能更为有益。相反，采用​​token选择路由（token-choice routing）​​ 的 MoR 则可以从 ​​KV 共享​​中受益，​​其较弱且不准确的路由决策（its weaker, inaccurate routing decisions）​​ 可以通过 ​​共享 KV 对提供的额外上下文信息（additional contextual information provided by shared KV pairs）​​ 得到补充。

---

Analysis​

1. 计算最优缩放分析 (Compute-optimal Scaling Analysis)​​

​​在等计算量（isoFLOPs）下，MoR 缩放更倾向于增大模型规模而非延长训练长度 (MoR scaling favors model size over training length under isoFLOPs)

如图 5a 所示，在​​等计算量约束（IsoFLOPs constraints）​​下，与基线模型相比，MoR 展现出​​独特的计算最优缩放行为（distinct compute-optimal scaling behavior）​​。

MoR ​​最优路径（optimal path）​​的​​更大斜率（larger slope）​​（即更接近零）表明，它从​​增加参数量（increases in parameter count）​​中获益更显著（即​​数据需求更低（less data-hungry）​​）。这可能是因为​​共享参数块（shared parameter block）​​本身的性能变得尤为重要，甚至比输入更多数据更重要。

因此，MoR 模型的​​最优缩放策略（optimal scaling policy）​​倾向于将资源分配给​​通过使用更大模型进行更短步数的训练来增加模型容量（increasing model capacity by using larger models trained for shorter steps）​​。

2. 路由分析 (Routing Analysis)​​

​​递归深度的分配反映了token的语义重要性 (The allocation of recursion depth reflects token semantic importance)​

在图 1 右侧，本文展示了一个​​token特定递归深度（token-specific recursion depths）​​的定性示例。第一个token“People”或​​富含内容的token（content-rich tokens）​​如“-ensively confident”和“Drugs”​​经过三个递归步骤（pass through three recursion steps）​​，而功能词（function words）如“and”、“---”和“∖n”则​​经过两个步骤（traverse two）​​。

相比之下，​​中等语义重要性的token（words of moderate semantic importance）​​通常​​仅经历一次递归（undergo only a single recursion）​​。这种模式表明，​​递归深度的分配（recursion depth allocation）​​与​​每个token的语义重要性（semantic importance of each token）​​紧密对应。

​​带辅助损失的专家选择路由器完美区分了选中与未选中的tokens (Expert-choice router with auxiliary loss perfectly separates selected from unselected tokens)

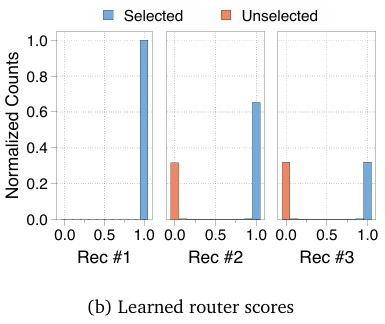
图 5b 可视化了一个示例，展示了在 Nr​=3 的 MoR 模型中，​​每个递归步骤（each recursion step）​​的​​专家选择路由器输出分布（expert-choice router output distribution）​​。对于每个递归步骤，绘制了​​路由分数（routing scores）​​的​​归一化计数（normalized counts）​​，区分了​​被专家选中的token（selected by the expert）​​（蓝色）和​​未被选中的token（not selected）​​（橙色）。在所有步骤中，​​辅助损失（auxiliary loss）​​在路由器输出中实现了​​完美分离（perfect separation）​​，被选中的token​​高度集中在接近 1.0 的路由分数附近（sharply concentrated near a routing score of 1.0）​​，而未选中的token则​​聚集在接近 0.0 的附近（clustering near 0.0）​​。

3. 测试时缩放分析 (Test-time Scaling Analysis)​​

​​MoR 通过更深递归实现测试时缩放 (MoR enables test-time scaling via deeper recursion)

​

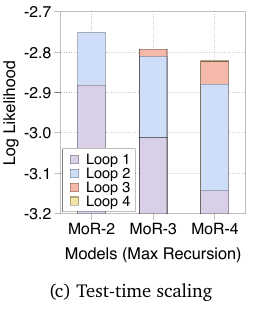
在图 5c 中可视化了在 Nr​={2,3,4} 的 MoR 模型中，​​对数似然（log-likelihood）​​如何随递归步骤演变。

叠加的条形图展示了当token的​​最大思考（递归）深度（maximum thinking (recursion) depth）​​逐渐增加时，每个模型的性能。这表明，​​更深的递归（deeper recursion）​​不仅提供了​​额外的计算资源（additional compute）​​，还使得​​每个后续步骤（each subsequent step）​​能够​​进一步专注于（specialize further）​​在其特定深度​​精炼token表示或“思考过程”（refining the token representation or “thought process”）​​，从而带来​​更好的性能（better performance）​​。

因此，这些结果支持了 ​​MoR 支持测试时缩放（MoR enables test-time scaling）​​的观点：在推理时​​分配更多的递归步骤（allocating more recursion steps at inference）​​可以​​提高生成质量（improve generation quality）​​。

---

Conclusion

1. 局限性与未来工作 (Limitations and Future Works)​​

​​推理型 MoR 模型 (Reasoning MoR models)​

最近的研究强调了​​推理链（reasoning chains）​​中的​​冗余性（redundancy）​​，并通过应用​​token级自适应计算（token-level adaptive computation）​​（如​​早退机制（early-exit mechanisms）​​）来解决它 。

本文的 MoR 框架通过​​自适应地确定单个token所需的递归深度（adaptively determining the necessary recursion depth for individual tokens）​​，​​内在地支持（inherently enables）​​ ​​隐式推理（latent reasoning）​​。

因此，一个关键的​​未来工作​​涉及探索当在​​实际的推理数据集（actual reasoning datasets）​​上进行​​后训练（post-trained）​​时，​​路由器（router）​​如何​​动态学习（dynamically learn）​​调整以适应​​思维链（chain-of-thought, CoT）​​的需求。

开发​​显式将递归深度与推理复杂度对齐（explicitly align recursion depth with reasoning complexity）​​的​​高级路由策略（advanced routing strategies）​​可能会​​提升推理准确率（enhance reasoning accuracy）、计算效率（computational efficiency）​​甚至​​可解释性​​。

​​进一步扩展模型家族 (Further scaling model family)

由于计算限制，实验仅限于​​参数规模最高达 17亿（up to 1.7 billion parameters）​​的模型。自然的下一步是在​​更大规模（over 3 billion parameters）​​和​​更大的语料库（substantially larger corpora）​​上训练 MoR 模型。

为了降低总体预训练成本，也可以探索​​持续预训练（continued pre-training）​​（即 ​​uptraining​​），从​​现有的预训练普通大语言模型检查点（existing pre-trained vanilla LLM checkpoints）​​开始。

本文计划研究使用​​递归模型的各种初始化策略（various initialization strategies for recursive models）的 MoR 性能。此外，为了确保​​公平的可扩展性比较（fair scalability comparison）​​，需要考虑递归 Transformer 在​​为早退而进行的后训练（post-training for early-exiting）​​期间可能出现的​​性能下降（performance degradation），并将​​普通 Transformer 的推理吞吐量约束（inference throughput constraints for Vanilla Transformers）​​纳入考量。

​​自适应容量控制 (Adaptive capacity control)​

专家选择路由（Expert-choice routing）​​具有通过​​预定义的容量因子（pre-determined capacity factors）​​保证​​完美负载均衡（perfect load balancing）​​的显著优势 (Raposo et al., 2024; Zhou et al., 2022)。然而，当本文在​​推理时（during inference）​​希望分配​​不同的容量（different capacities）​​时，就出现了一个限制。

具体来说，在本文的 MoR 模型中，观察到当使用​​辅助损失（auxiliary loss）​​时，​​被选中和未被选中token的路由器输出（router outputs for selected and unselected tokens）​​几乎是​​完美分离的（perfectly separated）​​。这使得在训练后调整 ​​top-k 值（adjust top-k values）​​变得困难。因此，需要一种​​更具适应性的模型设计（more adaptive model design）​​，能够在​​训练和推理阶段（both training and inference phases）​​利用不同的容量，以解决这一限制。

​​与稀疏算法的兼容性 (Compatibility with sparse algorithms)

鉴于 MoR 的​​token级自适应递归（token-level adaptive recursion）​​，本文可以通过​​集成结构化稀疏性（integrating structured sparsity）​​进一步优化计算。这种方法允许​​有选择地激活子网络或参数（selective activation of subnetworks or parameters），在​​token和层级别（both the token and layer levels）​​ ​​动态剪枝不必要的计算（dynamically pruning unnecessary computations）。这种对​​稀疏模型设计（sparse model designs）​​的探索有望带来​​显著的效率提升（significant efficiency improvements）​​。

作者相信许多​​基于稀疏性的技术（sparsity-based techniques）​​，如​​剪枝（pruning）或​​量化（quantization），与 MoR ​​高度互补（highly complementary）​​。这将为​​递归模型内有效的稀疏架构（effective sparse architectures within recursive models）​​提供更深入的见解，为未来研究指明有前景的方向。

​​扩展到多模态和非文本领域 (Expansion to multimodal and non-text domains)

MoR 的​​递归块本质上是​​模态无关的（modality-agnostic）​​，使其​​自适应深度机制（adaptive depth mechanism）​​能够​​扩展到文本处理之外（extend beyond text processing）​​。这一关键特性使 MoR 能够轻松集成到​​视觉、语音​​和​​统一的多模态 Transformer 架构（unified multimodal transformer architectures）​​中。

将​token自适应递归（token-adaptive recursion）​​应用于​​长上下文视频（long-context video）​​或​​音频流​​，有潜力实现​​更高的内存效率（even greater memory efficiencies）​​和​​显著的吞吐量提升（substantial throughput gains）​​，这对实际应用至关重要。通过​​动态调整每个token或片段（token or segment）的处理深度（dynamically adjusting the processing depth）​​，MoR 可以释放这些显著的优势。

---

原文有附录。