【算法】动态规划 · 上篇

1. 前缀和

1.1 一维前缀和

        用于快速计算数组中一段区间的和。

        准备前缀和数组：前缀和数组 i 下标位置的值表示原数组 0 ~ i 位置值的和。

        for (int i = 1; i <= 原数组的长度; i++) {dp[i] = dp[i - 1] + arr[i];}

 

        使用前缀和数组：

        arr[a] + arr[a+1] + ...... + arr[b] 即为 dp[b] - dp[a - 1]

1.2 二维前缀和

        给出一个 n 行 m 列的矩阵，x 表示行，y 表示列，求 (x1，y1) 到 (x2，y2) 这个子矩阵内元素的和。

        准备前缀和矩阵：前缀和矩阵中每个位置的值，都等于原矩阵中从 (0，0) 位置到这个位置的值的总和。如图前缀和矩阵中红色位置存放的值，应当为原矩阵的红框中全部值的和。想要快速求这个位置的值可以利用前缀和矩阵中绿色、黄色和蓝色位置的值，还需要原矩阵中这个位置的值。原矩阵中的绿色子矩阵加上蓝色子矩阵后多算了一个黄色子矩阵，因此要减去一个。

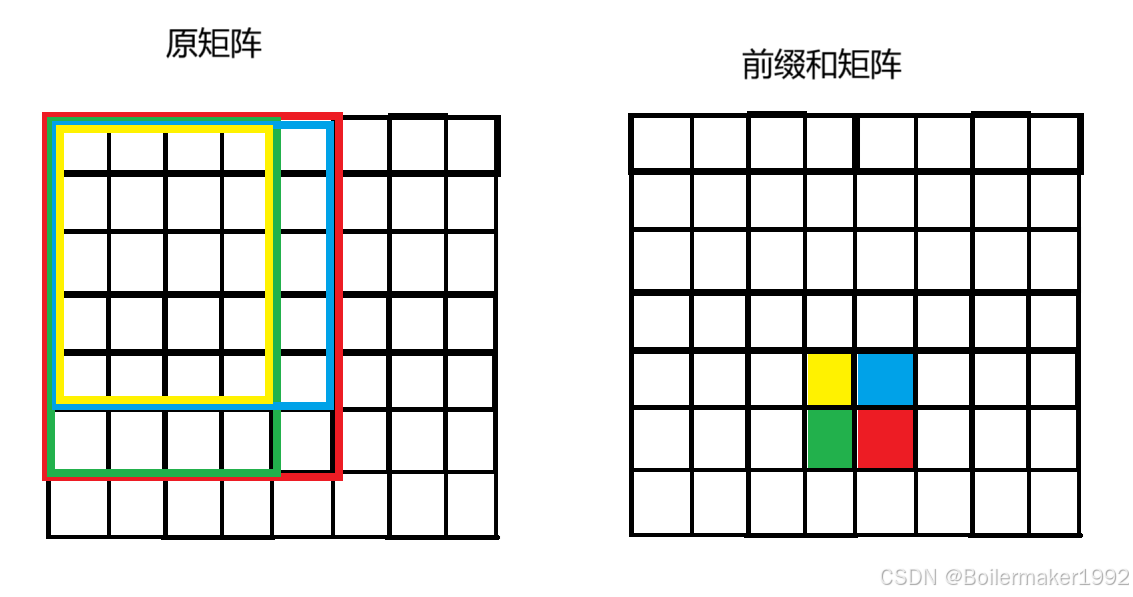
        for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {dp[i][j] = dp[i][j - 1] + dp[i - 1][j] +matrix[i][j] - dp[i - 1][j - 1];}}

        使用前缀和矩阵：

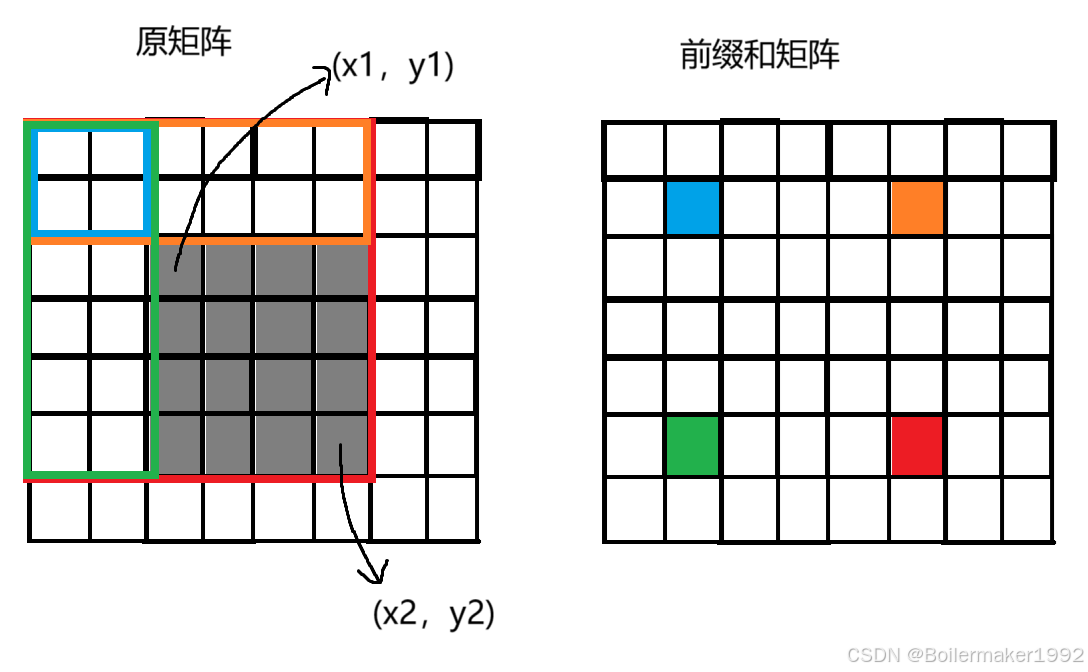
        dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]

1.3 前缀和与后缀和

724. 寻找数组的中心下标 - 力扣（LeetCode）

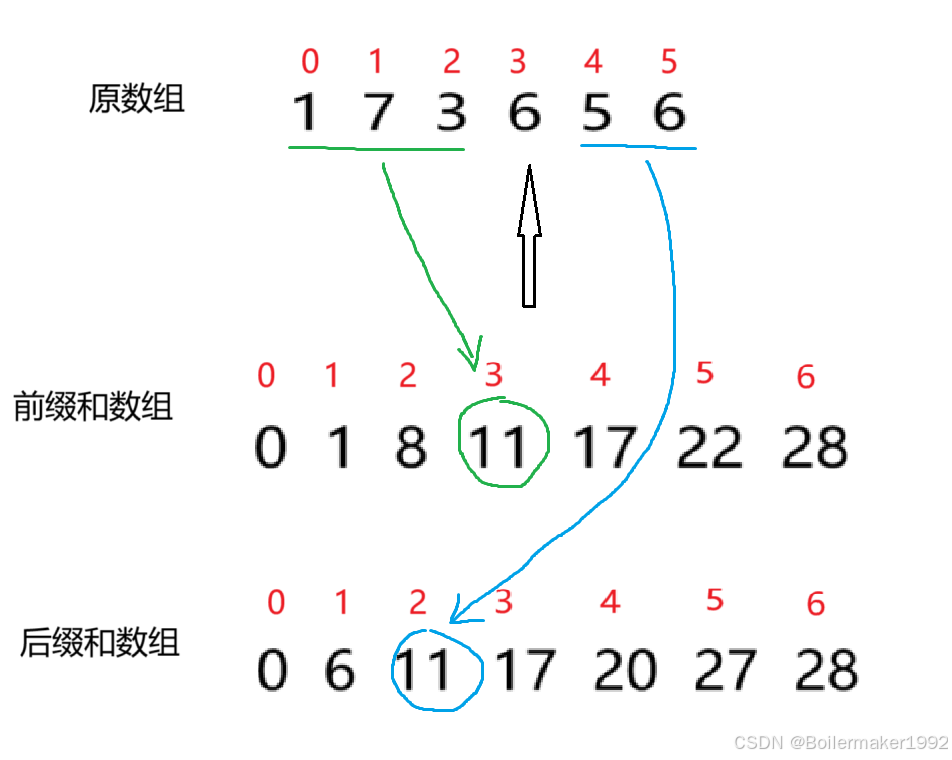
        找数组中的一个位置，这个位置左侧所有元素的和等于右侧所有元素的和，返回下标。左侧所有元素的和需要前缀和数组，右侧所有元素的和需要后缀和数组。

        准备两个数组：

       

        for (int i = 1; i <= len; i++) {prefix[i] = prefix[i - 1] + nums[i - 1];postfix[i] = postfix[i - 1] + nums[len - i];}

        使用数组：原数组中定义指针，指向 i 位置时，判断 prefix[i] 是否等于 postfix[len - 1 - i] 即可。

238. 除自身以外数组的乘积 - 力扣（LeetCode）

1.4 前缀和与哈希表

问题转化

560. 和为 K 的子数组 - 力扣（LeetCode）

                

class Solution {public int subarraySum(int[] nums, int k) {Map<Integer, Integer> hash = new HashMap<>();hash.put(0, 1);int sum = 0, count = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];count += hash.getOrDefault(sum-k, 0);hash.put(sum, hash.getOrDefault(sum, 0)+1);}return count;}
}

同余定理

974. 和可被 K 整除的子数组 - 力扣（LeetCode）

关键点 1：使用同余定理

        若 a - b 能被 c 整除，则 a 和 c 相除的余数 = b 和 c 相除的余数。

        在这道题里利用：

                

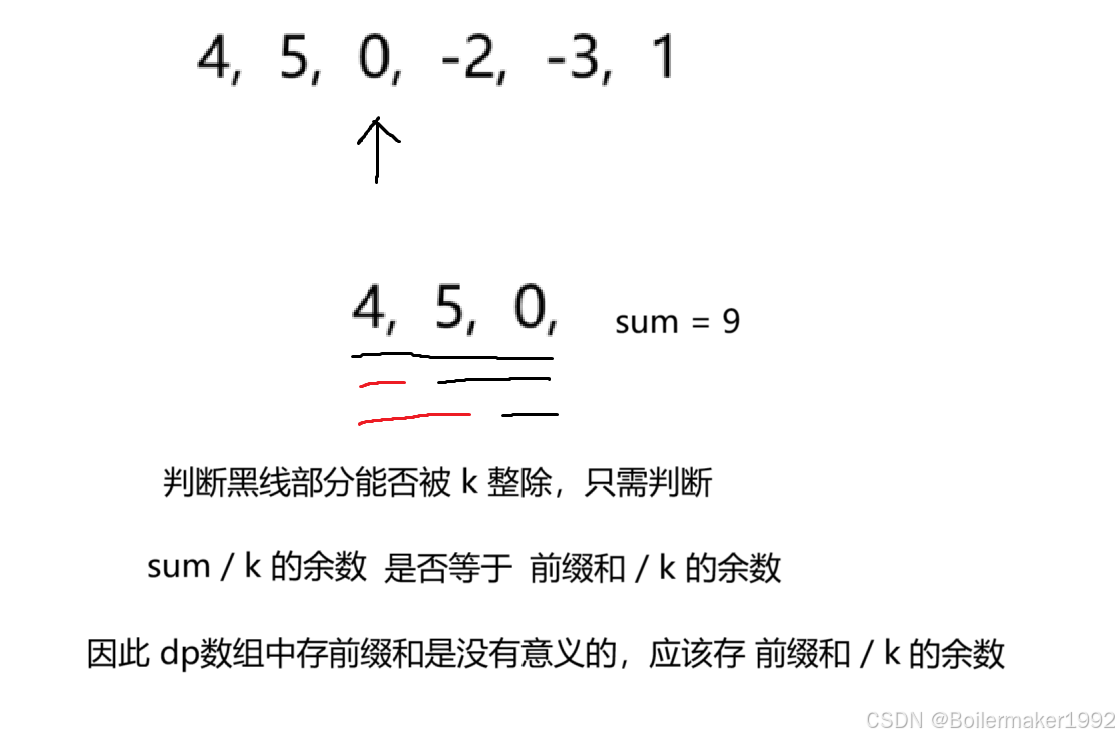
        思路：关键是如何利用之前已计算的值。前一道题是 sum - k = prefix，所以应该将前缀和存入 hash；这一道题是 sum % k = prefix % k，所以应该将 prefix % k 存入 hash。

关键点 2：Java 取余运算

                

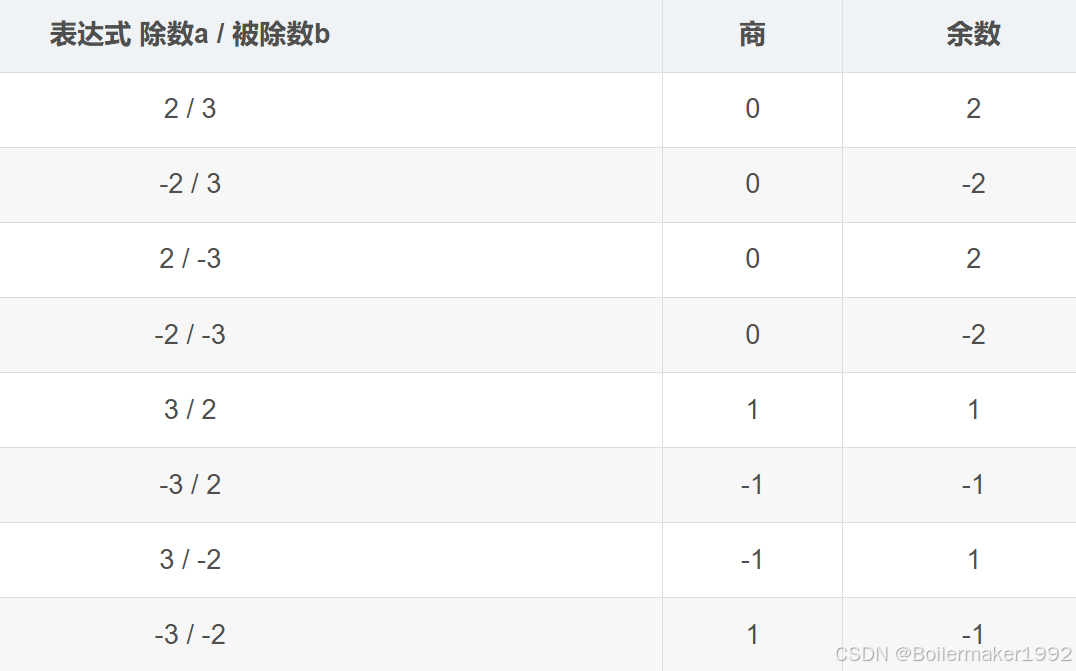
        商和余数的值：除数和被除数都加绝对值运算。

        商的符号：看除数和被除数的符号是否一致，同正异负。

        余数的符号：跟除数保持一致。

        这道题需要避免余数出现负数，负数余数是 C++、Java 的计算方法，可以转化为正数余数。题目中被除数可能为负数，但除数 k 不可能为负数。

        有两种方法：

// 增加一步的步长以保证余数为正
1. int r = (sum % k + k) % k;
// Math.floorMod用于计算数学上正确的模运算，它在处理负数时能提供更符合数学直觉的结果。
// 推荐确保除数为正。
2. int r = Math.floorMod(sum, k);

class Solution {public int subarraysDivByK(int[] nums, int k) {Map<Integer, Integer> hash = new HashMap<>();hash.put(0, 1);int sum = 0, count = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];int r = (sum % k + k) % k;count += hash.getOrDefault(r, 0);hash.put(r, hash.getOrDefault(r, 0) + 1);}return count;}
}

2. 斐波那契数列模型

面试题 08.01. 三步问题 - 力扣（LeetCode）

        状态表示：dp[i] 表示小孩上 i 阶楼梯共有多少方法。

        状态转移方程：对于任意一阶楼梯，小孩要么是跨一阶楼梯上来的，要么是跨两阶楼梯上来的，要么是跨三阶楼梯上来的。因此，dp[i] = dp[i-1] + dp[i-2] + dp[i-3]。

        

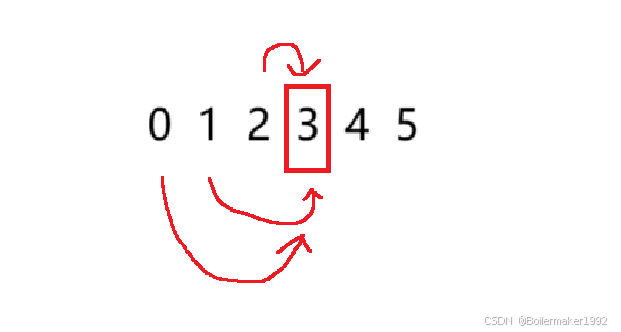
        初始化：数组前三个元素作为辅助节点，n=1 在第四个位置。n=1 时只有一种方法，所以 dp[0] + dp[1] + dp[2] 应该等于 1，n=2 时有两种方法，dp[1] + dp[2] + dp[3] 应该等于 2。综上，初始化三个辅助节点的值分别为 1，0，0。

        细节：可以循环数字来降低空间复杂度。

91. 解码方法 - 力扣（LeetCode）

        状态表示：dp[i] 表示到第 i 个位置共有多少种编码方法。

        状态转移方程：

                对于 dp[i] 来说，要么它可以自己被编码，要么它可以和前一位组合编码，要么它就是既可以自己编码，也可以和前一位组合编码。

                情况1：dp[i] 只能单独编码。此时说明 dp[i] 一定不等于 0，且 dp[i-1] 和 dp[i] 组合成的数字不在 10 - 26 之间。这个时候，dp[i] 应当等于 dp[i-1]。

                情况2：dp[i] 只能组合编码。此时说明 dp[i] 一定等于 0，且 dp[i-1] 和 dp[i] 组合成的数字在 10 - 26 之间。这个时候，dp[i] 应当等于 dp[i-2]。

                情况3：dp[i] 既能单独编码，也能组合编码。此时说明 dp[i] 一定不等于 0，且 dp[i-1] 和 dp[i] 组合成的数字在 10 - 26 之间。这个时候，dp[i] 应当等于 dp[i-1] + dp[i-2]。

                情况4：dp[i] 既不能单独编码，也不能组合编码。此时说明 dp[i] 一定等于 0，且 dp[i-1] 和 dp[i] 组合成的数字不在 10 - 26 之间。这个时候，说明在这个位置无法被编码，应当直接返回 0。

        初始化：对于题目给的字符串的每一位，我们在判断时都需要看它的前一位。对于 dp 数组的每个元素来说，我们每次都需要看它的前两位。为保证不越界，循环应当从字符串的第二位，dp 的第三位开始。因此字符串的第一位和 dp 的前两位应当特殊考虑。

class Solution {public int numDecodings(String ss) {// 准备工作char[] s = ss.toCharArray();int len = s.length;int[] dp = new int[len + 1];// 初始化if (s[0] == '0') {return 0;}dp[0] = 1;dp[1] = 1;// 填表for (int i = 2; i < len + 1; i++) {// 单独编码if (s[i - 1] != '0') {dp[i] += dp[i - 1];}// 组合编码int temp = (s[i - 2] - '0') * 10 + (s[i - 1] - '0');if (temp >= 10 && temp <= 26) {dp[i] += dp[i - 2];}/* 循环到这里，如果前面的 if 都没有满足，说明在这个位置已经* 无法被编码，直接返回 0 即可 */if (dp[i] == 0) {return 0;}}return dp[len];}
}

3. 路径问题

62. 不同路径 - 力扣（LeetCode）

        状态表示：dp[i][j] 表示从 (1, 1) 到 (i, j) 共有多少条路线。

        状态转移方程：要么从上面的格子走到 dp[i][j]，要么从左面的格子走到 dp[i][j]。因此 dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

        

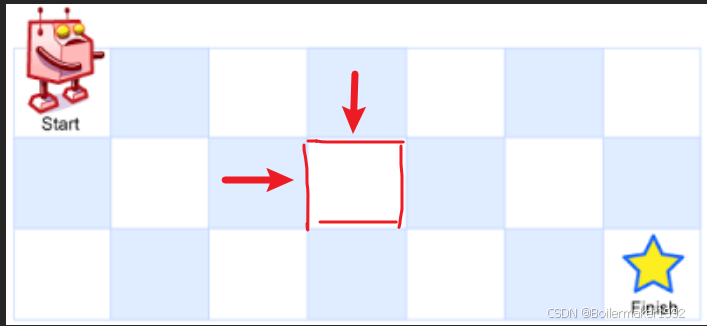
        初始化：使用辅助节点，dp[1][1] 应该等于 1，所以将 dp[1][0] 初始化为 1，其他地方依然为 0。

        细节：填 dp 表时，从左向右从上往下依次填即可，因为对于每个位置我们只需要它上面的元素和左面的元素。

931. 下降路径最小和 - 力扣（LeetCode）

        状态表示：dp[i][j] 表示下降到此位置，花费的最小值。

        状态转移方程：对于每个位置，只有可能从这三个方向到达，再加上自己本身，就是到这个位置花费的最小值了。因此，dp[i][j] = dp 表中这三个位置的最小值 + matrix[i - 1][j - 1]。

        

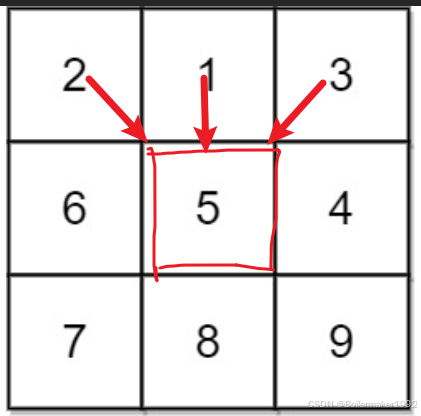
        初始化：使用辅助节点，上面一行，左右各一列。最左和最右列设置为不可能被取到的值。

        

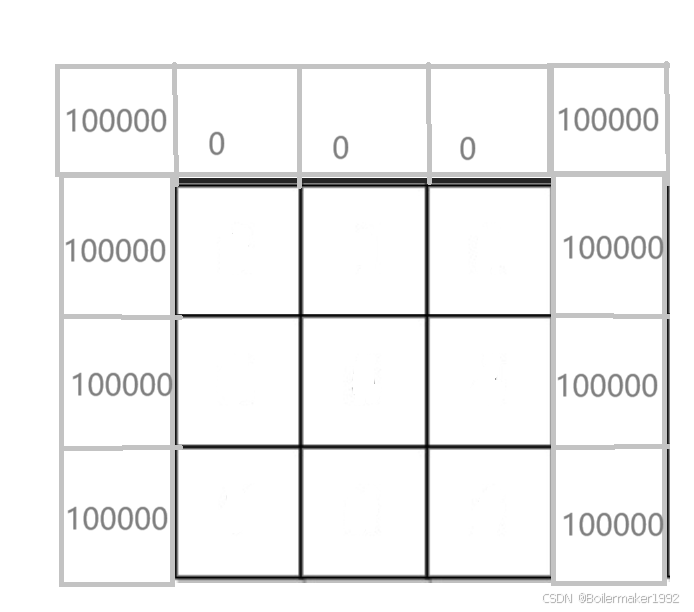
        细节：返回最后一行中最小的元素。

174. 地下城游戏 - 力扣（LeetCode）

        状态表示：这道题需要使用不同的状态表示方式，dp[i][j] 表示以该位置为起点，到终点所需最低血量。

        状态转移方程：对于每个元素，只有向右和向下移动这两种情况，选择 dp 表中这两个位置中较小的，再减去自己本身，就是这个元素到终点所需最低血量。如果这个所需最低血量小于等于 0，说明从这个位置到终点不需要初始血量，由于题目规定骑士的血量必须是正整数，因此此时将血量设为 1。

        

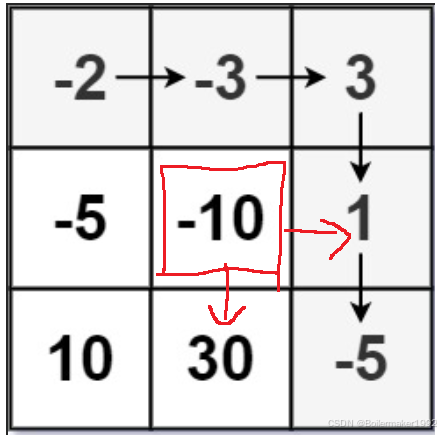
        初始化：使用辅助节点，最右一列和最下一行均设为无法取到的元素，但除了 (m-1, n) 或 (m, n-1) 的位置应设为 1。因为对于终点位置的元素，如果为负数，初始血量应为其倒数加一。

        细节：填表时要倒序。

4. 简单多状态

面试题 17.16. 按摩师 - 力扣（LeetCode）

        

213. 打家劫舍 II - 力扣（LeetCode）

        思路与上一道题基本类似，只是这道题变成了环形数组。因此，偷 1 号房间则不能偷 2 号房间和最后一间房间，那么，1 号房间的逻辑实际上不同于其他房间，因为 1 号房间会影响两间。为了将问题一般化，我们可以分别考虑 1 号房间和最后的房间，也就是不要在一次循环中同时考虑这两间。

class Solution {public int rob(int[] nums) {int len = nums.length;if (len == 1)return nums[0];// 调用两次 plunder，第一次包括第一间不包括最后一间，第二次不包括第一间包括最后一间return Math.max(plunder(nums, 0, len - 1), plunder(nums, 1, len));}private int plunder(int[] nums, int start, int end) {int len = nums.length;int[] dp1 = new int[len + 1];int[] dp2 = new int[len + 1];for (int i = start + 1; i < end + 1; i++) {dp1[i] = dp2[i - 1] + nums[i - 1];dp2[i] = Math.max(dp1[i - 1], dp2[i - 1]);}return Math.max(dp1[end], dp2[end]);}
}

740. 删除并获得点数 - 力扣（LeetCode）

        每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除所有等于 nums[i] - 1 和 nums[i] + 1 的元素。

        题目分析：在数组排好序的情况下，如果删除 nums[i]，则可以获得全部等于 nums[i] 的元素的点数，然后与其点数相邻的元素就都不能选了。这道题可以转化为打家劫舍问题，它们都是相邻不选。这道题需要先将数据预处理，因为单独考虑每一个元素其实比较麻烦，我们可以直接先统计好每组相等元素的总和。之后就是打家劫舍问题了。

        

class Solution {public int deleteAndEarn(int[] nums) {// 将数据预处理到 hash，转化为打家劫舍// 使用 size 来做优化int size = 0;for (int n : nums) {size = Math.max(size, n) + 1;}int[] hash = new int[size];for (int i = 0; i < nums.length; i++) {hash[nums[i]] += nums[i];}// 打家劫舍int[] dp1 = new int[size];int[] dp2 = new int[size];for (int i = 1; i < size; i++) {dp1[i] = dp2[i - 1] + hash[i];dp2[i] = Math.max(dp1[i - 1], dp2[i - 1]);}return Math.max(dp1[size - 1], dp2[size - 1]);}
}

LCR 091. 粉刷房子 - 力扣（LeetCode）

        这是比较简单的一道题。与之前的不同点是，这道题需要使用三个状态表示，但思路是完全一致的。每一栋房子都可能被漆成三种颜色，分别表示即可。

309. 买卖股票的最佳时机含冷冻期 - 力扣（LeetCode）

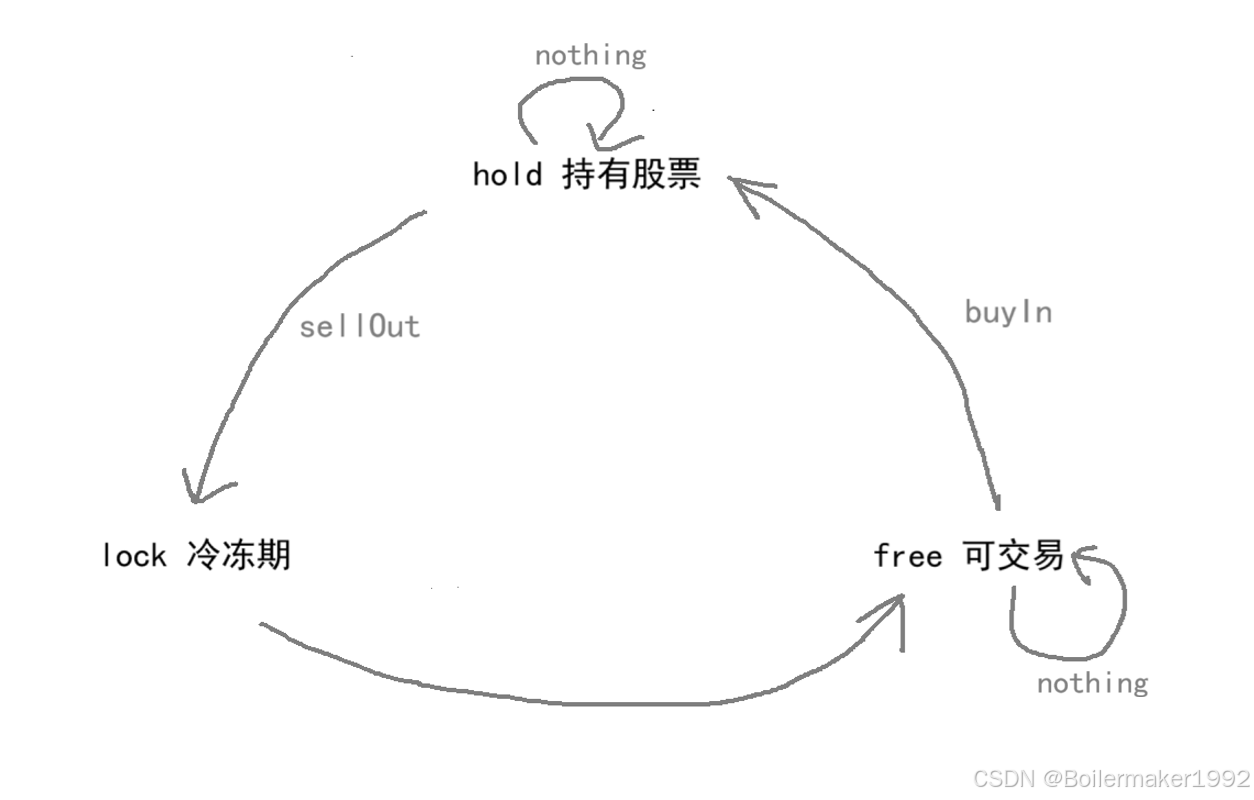
        这道题的状态比较难考虑。根据题意，分为三种状态：持有股票（hold），处于冷冻期（lock），可以正常参与交易（free）。题目中其实给了我们三种状态，分别是买入、卖出和冷冻期。但是这样表示比较乱，因为有可能在这个位置什么都没做，没买入也没卖出，也没处于冷冻期。买入和卖出是动作，不是状态。

        接下来分析这三种状态之间的关系：

        hold：

        -> 保持状态：原先持有股票，希望继续持有，什么都不做即可。

        -> free：把手头的股票卖了，再经历一天的冷冻期，才能继续参与交易。不能直接从 hold 转化成 free，必须经历冷冻期。

        -> lock：抛售股票后就会到这个状态。

        free：

        -> 保持状态：什么都不做即可。

        -> hold：买入股票则变为持有股票的状态。

        -> lock：free 变不到 lock。

        lock：

        -> 保持状态：冷冻期规定为 1 天，不可能延长，所以不能保持状态。

        -> hold：lock 不能直接变为 hold，必须先变为 free，free 才是可交易状态。

        -> free：一个周期后 lock 解除，变为 free。

        

class Solution {public int maxProfit(int[] prices) {int len = prices.length;int[] hold = new int[len];int[] lock = new int[len];int[] free = new int[len];hold[0] = -prices[0];for (int i = 1; i < len; i++) {hold[i] = Math.max(hold[i - 1], free[i - 1] - prices[i]);lock[i] = hold[i - 1] + prices[i];free[i] = Math.max(free[i - 1], lock[i - 1]);}int ret = Math.max(Math.max(hold[len - 1], lock[len - 1]), free[len - 1]);return ret;}
}

188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

        状态分析：

        这道题限制了交易的次数，因此状态不只有 hold 和 free 两个，而是要将交易的次数也作为状态考量。对于 hold 来说，考虑这是第几次持有股票；对于 free 来说，考虑这是第几次处于自由状态。因此使用二维数组来分别表示 hold 和 free。

        每一次交易是一个 free 和 hold 之间的循环，并且，将 free 设为循环的起点会使问题比较简单。此时，状态变化类似这样：第一次处于自由状态 -> 第一次持有股票 -> 第二次处于自由状态 -> 第二次持有股票 -> 第三次处于自由状态 -> 第三次持有股票 ……

        另外，处于 free 状态的情况应当比 hold 多一次。hold 状态只能出现 k 次，但第 k 次 hold 后依然可以有第 k + 1 次 free。并且，状态变化的终点肯定是 free，因为在最后一个位置买入股票只会亏钱。因此，数组最后一个位置的 hold 状态不需要计算。

        状态表示：

        free[i][j] 表示截止到第 i 天，进行 j 次交易后，处于自由状态，此时可以获得的最大利益。hold[i][j] 表示截止到第 i 天，进行 j 次交易后，处于持有股票的状态，此时可以获得的最大利益。

        状态转移方程：

free[i][j] = Math.max(free[i - 1][j], hold[i - 1][j - 1] + prices[i]);
hold[i][j] = Math.max(hold[i - 1][j], free[i - 1][j] - prices[i]);

        初始化：

        使用分类讨论和直接初始化，不使用辅助节点。free(1,0) 需要 free(0,0) 和 hold(0,-1)，这里使用分类讨论。当 j < 1 时，直接让 free[i][j] = free[i - 1][j] 即可，其他时候再考虑 hold[i - 1][j - 1]。

        

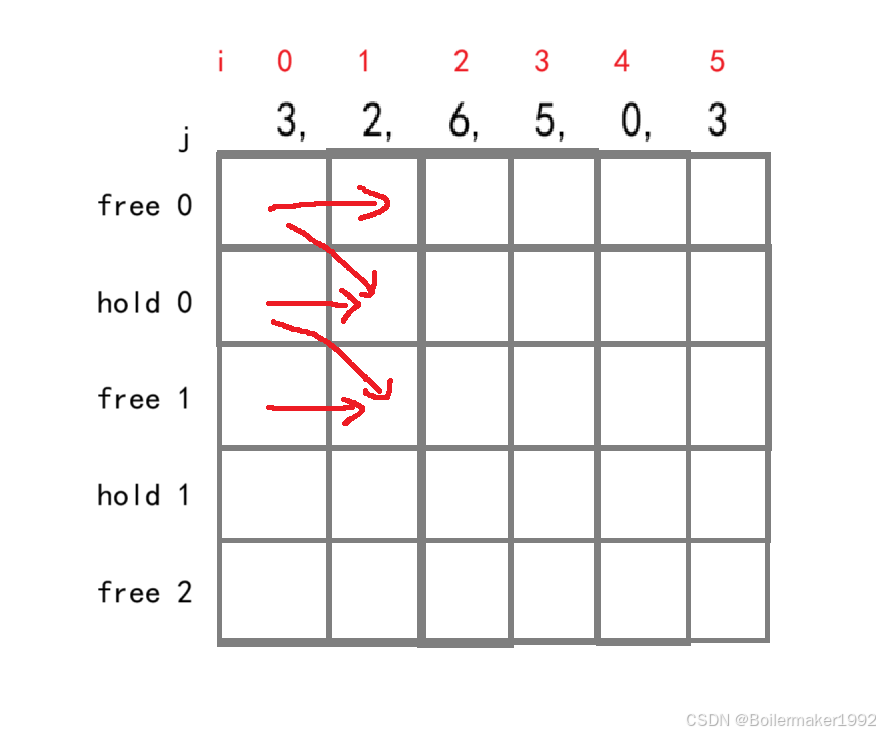
        想让初始状态为 free，什么都不做即可，free(0,0) 应初始化为 0。想让初始状态为 hold，买入首日股票即可，hold(0,0) 应初始化为 -prices[0]。在第一日（i = 0），不可能达到第二次自由状态或第二次持有股票的状态，j > 0 的地方都应该设为无法被取到的值（MIN）。 这些 MIN 会通过状态转移方程传递。

        

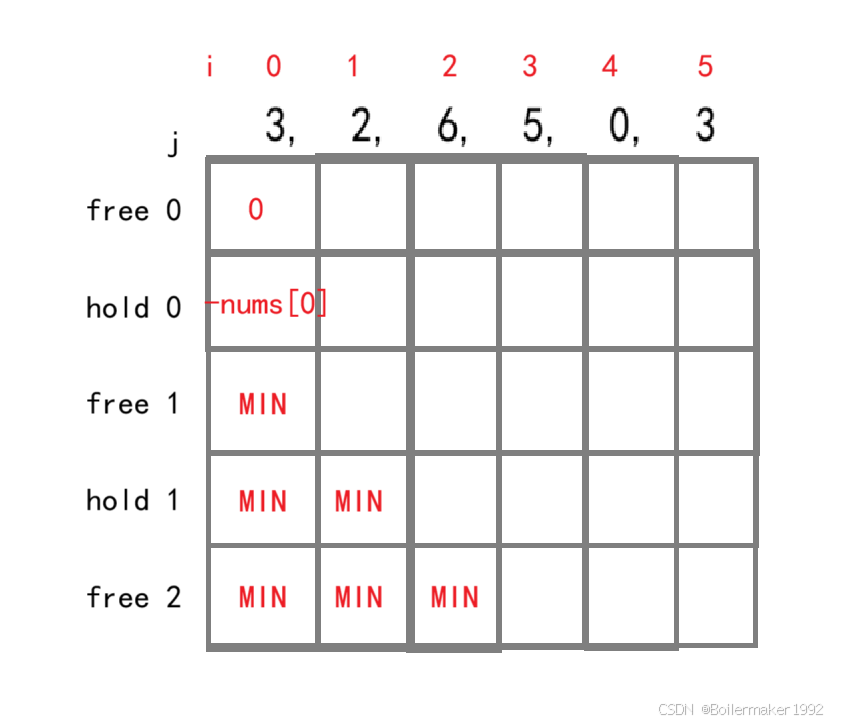
        返回值：

        由于状态变化的终点肯定是 free，找到截止最后一天，进行几次交易的 free 值最大。

        完整代码：

class Solution {public int maxProfit(int k, int[] prices) {// 准备工作int len = prices.length;if (len == 1) {return 0;}int MIN = -0x3f3f3f3f;int[][] free = new int[len][k + 1];int[][] hold = new int[len-1][k];// 初始化for (int j = 1; j < k + 1; j++) {free[0][j] = MIN;if (j < k) {hold[0][j] = MIN;}}free[0][0] = 0;hold[0][0] = -prices[0];// 二维 dpfor (int i = 1; i < len; i++) {for (int j = 0; j < k + 1; j++) {if (j >= 1) {free[i][j] = Math.max(free[i - 1][j], hold[i - 1][j - 1] + prices[i]);} else {free[i][j] = free[i - 1][j];}if (j < k && i < len - 1) {hold[i][j] = Math.max(hold[i - 1][j], free[i - 1][j] - prices[i]);}}}// 返回结果int ret = MIN;for (int j = 0; j < k + 1; j++) {ret = Math.max(free[len - 1][j], ret);}return ret;}
}

        空间优化：

        在 i 天内，最多完成 i / 2 次交易，若 k > i / 2，就一定会有多余的可交易次数，此时使 k 直接等于 i / 2 即可。 

        在没有交易次数限制的时候，两个一维 dp 数组可以简化为两个 int，在这里也是同理，二维 dp 数组可以简化为一维 dp 数组。

        简化后的状态表示：free[j] 表示进行 j 次交易后，处于自由状态，此时可以获得的最大利益。hold[j] 表示进行 j 次交易后，处于持有股票状态，此时可以获得的最大利益。

        简化后的状态转移方程：

hold[j] = Math.max(hold[j], free[j - 1] - price);
free[j] = Math.max(free[j], hold[j] + price);

        简化后的返回值：hold 和 free 都是严格递增的，因此返回 free 的最后一个值即可。

        优化后的代码： 

class Solution {public int maxProfit(int k, int[] prices) {// 准备工作k = Math.min(k, prices.length / 2);int[] hold = new int[k + 1];int[] free = new int[k + 1];// 初始化int MIN = -0x3f3f3f3f;Arrays.fill(hold, MIN);// 二维 dpfor (int price : prices) {for (int j = 1; j < k + 1; j++) {hold[j] = Math.max(hold[j], free[j - 1] - price);free[j] = Math.max(free[j], hold[j] + price);}}// 返回值return free[k];}
}

5. 子串问题

918. 环形子数组的最大和 - 力扣（LeetCode）

        

class Solution {public int maxSubarraySumCircular(int[] nums) {int overall = 0;int len = nums.length;for (int i = 0; i < len; i++) {overall += nums[i];}int temp = overall - minSubArray(nums);if (temp == 0) {return maxSubArray(nums);} else {return Math.max(temp, maxSubArray(nums));}}private int maxSubArray(int[] nums) {int len = nums.length;if (len == 1) {return nums[0];}int dp = nums[0];int ret = nums[0];for (int i = 1; i < len; i++) {dp = Math.max(nums[i], dp + nums[i]);ret = Math.max(ret, dp);}return ret;}private int minSubArray(int[] nums) {int len = nums.length;if (len == 1) {return nums[0];}int dp = nums[0];int ret = nums[0];for (int i = 1; i < len; i++) {dp = Math.min(nums[i], dp + nums[i]);ret = Math.min(ret, dp);}return ret;}
}

1567. 乘积为正数的最长子数组长度 - 力扣（LeetCode）

        状态表示：

        以该位置为结尾的，乘积为正的最长子数组。

        以该位置为结尾的，乘积为负的最长子数组。

        分析：

        正数不会改变正负号，所以如果碰到正数，直接在其前一个位置记录的最长子数组基础上 + 1 即可。但负数会改变正负号，如果碰到负数，仅仅记录乘积为正的最长子数组是不够的，状态转移不过去。

class Solution {public int getMaxLen(int[] nums) {// 准备工作int len = nums.length;int[] pos = new int[len + 1];int[] neg = new int[len + 1];int tempMax = 0;// 初始化pos[0] = 0;neg[0] = -1;// dpfor (int i = 1; i < len + 1; i++) {if (nums[i - 1] > 0) {pos[i] = pos[i - 1] + 1;neg[i] = neg[i - 1] == -1 ? -1 : neg[i - 1] + 1;} else if (nums[i - 1] < 0) {pos[i] = neg[i - 1] + 1;neg[i] = pos[i - 1] + 1;} else {pos[i] = 0;neg[i] = -1;}tempMax = Math.max(tempMax, pos[i]);}// 返回结果return tempMax;}
}

978. 最长湍流子数组 - 力扣（LeetCode）

        与上一道题类似的思路

139. 单词拆分 - 力扣（LeetCode）

        dp[i] 表示以 i 为结尾，之前的部分能不能利用字典表示。因此 dp 中存 boolean。

        假设 i 位于如图所示位置，那么此时就需要另一个指针 j，来与 i 共同尝试截出一个词典中已有的单词。如果截不出来，则以 i 为结尾的部分不能用字典表示。如果能截出来，那表示从 j 到 i 是一个合法单词，然后再根据 dp 表，查看 j - 1 的位置能不能用字典表示，如果能的话，说明 i 位置为结尾的部分能用字典表示。

        

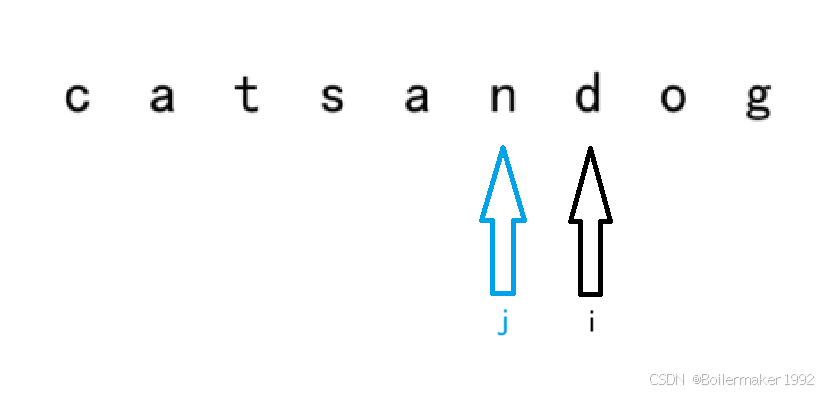
class Solution {public boolean wordBreak(String s, List<String> wordDict) {// 将 List 中的元素复制到 Set 中，方便查找Set<String> hash = new HashSet<>(wordDict);// 初始化int len = s.length();boolean[] dp = new boolean[len + 1];dp[0] = true;// dpfor (int i = 1; i < len + 1; i++) {for (int j = i; j > 0; j--) {if (hash.contains(s.substring(j - 1, i))) {dp[i] = dp[j - 1];if (dp[i] == true) {break;}}}}// 返回结果return dp[len];}
}

467. 环绕字符串中唯一的子字符串 - 力扣（LeetCode）

        dp[i] 表示，有多少以 i 为结尾的子字串，在 base 中出现。

        需要注意的是，s 中会有重复的字符。但在统计的时候，我们并不知道哪一个能构成合法子串的数量比较多。比如，bcabc，以第一个 c 为结尾的合法子串为 c、bc 这两个。而以第二个 c 为结尾的合法子串为 c、bc、abc 这三个。因此，我们必须统计 s 中的每一个字符，重复的字符保留最大值即可。

class Solution {public int findSubstringInWraproundString(String s) {// 特殊讨论if (s.length() == 1) {return 1;}// 初始化int[] hash = new int[26];hash[(int)s.charAt(0) - 97] = 1;int dp = 1;// dpfor (int i = 1; i < s.length(); i++) {int pre = (int)s.charAt(i - 1);int cur = (int)s.charAt(i);if (cur == pre + 1 || (cur == 'a' && pre == 'z')) {dp++;} else {dp = 1;}hash[cur - 97] = Math.max(hash[cur - 97], dp);}// 返回值int sum = 0;    for (int val : hash) {sum += val;}return sum;}
}