算法思想之队列

欢迎拜访：雾里看山-CSDN博客
本篇主题：算法思想之队列
发布时间：2025.7.24
隶属专栏：算法

算法介绍

队列（Queue）是一种遵循 “先进先出”（First In, First Out, FIFO） 原则的线性数据结构，其操作特性类似于现实生活中的排队场景（如银行排队、打印机任务队列）。队列在算法设计、系统开发中应用广泛，是基础且重要的数据结构之一。

队列的基本概念与特性

定义：队列是仅允许在一端（队尾，Rear） 插入元素，在另一端（队头，Front） 删除元素的线性数据结构。

• 队头（Front）：允许删除元素的一端（类似排队时的 “最前面”）。
• 队尾（Rear）：允许插入元素的一端（类似排队时的 “最后面”）。
• 空队列：不含任何元素的队列。

关键特性：

• FIFO 原则：最早入队的元素最先出队（先到先服务）。
• 操作受限：仅支持两种核心操作：
• 入队（Enqueue）：在队尾插入元素。
• 出队（Dequeue）：在队头删除并返回元素。
• 此外，通常还支持 Peek 操作（查看队头元素但不删除）和 isEmpty 操作（判断队列是否为空）。

队列的经典算法与问题

1. 滑动窗口最大值
2. 广度优先搜索（BFS）
3. 队列的顺序实现与基本操作
4. 用栈实现队列

应用场景与注意事项

典型应用：

• 任务调度：操作系统的进程调度、打印机任务队列，按请求顺序处理任务。
• 缓冲机制：网络通信中的数据缓冲区（如 TCP 协议的滑动窗口），平衡数据生产和消费速度。
• 广度优先搜索（BFS）：树的层序遍历、图的最短路径（如无权图的最短路径）。
• 消息队列：分布式系统中用于异步通信（如 RabbitMQ、Kafka），解耦生产者和消费者。
• 滑动窗口问题：如求子数组的最大值、字符串中不含重复字符的最长子串等。

注意事项与优化：

• 边界条件：处理队列空 / 满状态，避免出队时访问空队列或入队时超出容量。
• 效率优化：
  • 循环队列比普通数组队列空间利用率更高，适合固定大小场景。
  • 链式队列适合动态大小场景，但需注意内存碎片问题。
• 双端队列（Deque）：允许两端入队 / 出队，结合了队列和栈的特性，适合滑动窗口等场景。

例题

N 叉树的层序遍历

题目链接

429. N 叉树的层序遍历

题目描述

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

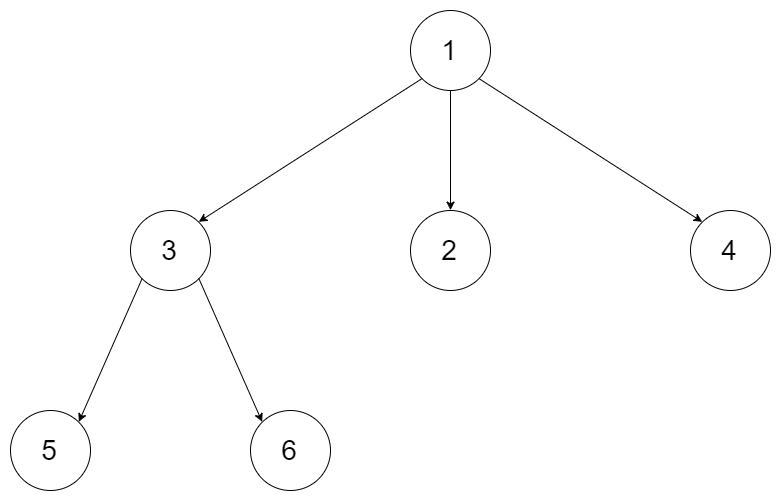
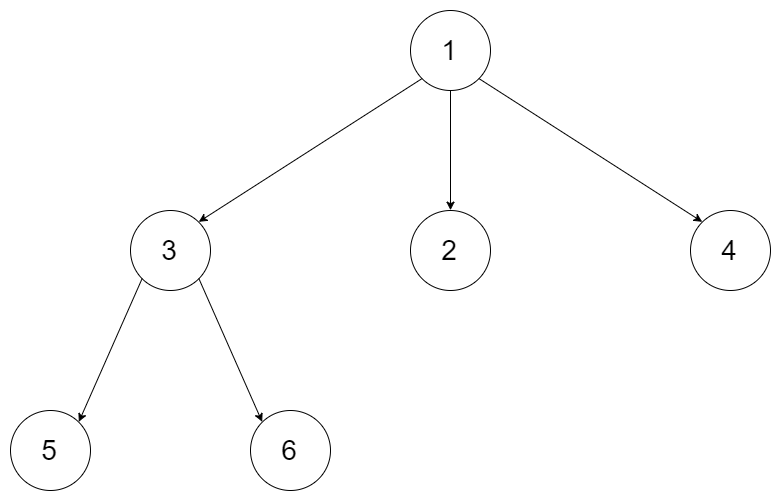
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

• 树的高度不会超过 1000
• 树的节点总数在 [0, 104] 之间

算法思路

层序遍历即可~
仅需多加一个变量，用来记录每一层结点的个数就好了。

代码实现

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret;if(root == nullptr)return ret;queue<Node*> q;q.push(root);vector<int> tmp;tmp.push_back(root->val);ret.push_back(tmp);while(!q.empty()){vector<int> tmp;int n = q.size();for(int i = 0; i < n; i++){Node *t = q.front();q.pop();vector<Node*> ch = t->children;for(auto &it : ch){tmp.push_back(it->val);q.push(it);}}if(!tmp.empty())ret.push_back(tmp);}return ret;}
};

二叉树的锯齿形层序遍历

题目链接

103. 二叉树的锯齿形层序遍历

题目描述

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

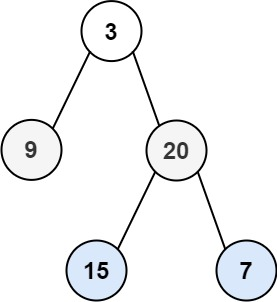
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -100 <= Node.val <= 100

算法思路

在正常的层序遍历过程中，我们是可以把一层的结点放在一个数组中去的。
既然我们有这个数组，在合适的层数逆序就可以得到锯齿形层序遍历的结果。

代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> ret;if(root == nullptr) return ret;queue<TreeNode*> q;q.push(root);int level = 1;while(!q.empty()){vector<int> tmp;int n = q.size();for(int i = 0; i < n; i++){TreeNode *t = q.front();q.pop();tmp.push_back(t->val);if(t->left)q.push(t->left);if(t->right)q.push(t->right);}if(level%2 == 0)reverse(tmp.begin(),tmp.end());level++;ret.push_back(tmp);} return ret;}
};

二叉树最大宽度

题目链接

662. 二叉树最大宽度

题目描述

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

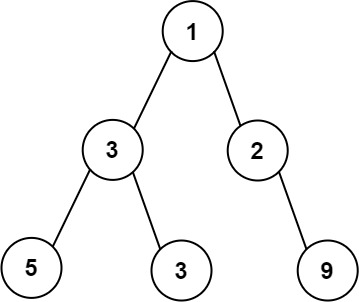
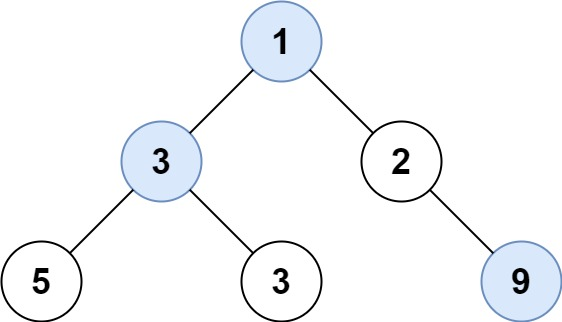
输入：root = [1,3,2,5,3,null,9]
输出：4
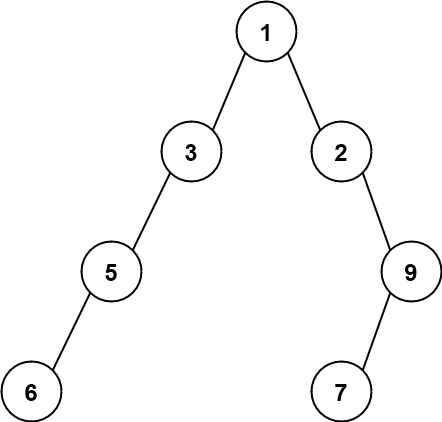
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

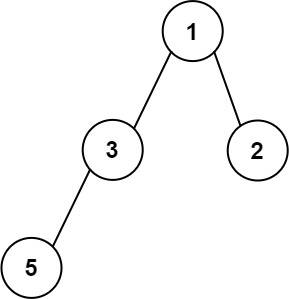
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

• 树中节点的数目范围是 [1, 3000]
• -100 <= Node.val <= 100

算法思路

利用二叉树的顺序存储 - 通过根节点的下标，计算左右孩子的下标

利用层序遍历，队列里面不单单存结点信息，并且还存储当前结点如果在数组中存储所对应的下标（在我们学习数据结构 - 堆的时候，计算左右孩子的方式）。

这样我们计算每一层宽度的时候，无需考虑空节点，只需将当层结点的左右结点的下标相减再加 1 即可。

但是，这里有个细节问题：如果二叉树的层数非常恐怖的话，我们任何一种数据类型都不能存下下标的值。但是没有问题，因为

• 我们数据的存储是一个环形的结构；
• 并且题目说明，数据的范围在 int 这个类型的最大值的范围之内，因此不会超出一圈；
• 因此，如果是求差值的话，我们无需考虑溢出的情况。

代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int widthOfBinaryTree(TreeNode* root) {unsigned int ret = 0;vector<pair<TreeNode*, unsigned int>> q;q.push_back({root,1});while(q.size()){auto [x1,y1] = q[0];auto [x2,y2] = q.back();ret = max(ret, y2-y1+1);vector<pair<TreeNode*, unsigned int>> tmp;for(auto& [x,y]: q){if(x->left)tmp.push_back({x->left, y*2});if(x->right)tmp.push_back({x->right, y*2+1});}q = tmp;} return ret;}
};

在每个树行中找最大值

题目链接

515. 在每个树行中找最大值

题目描述

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

示例2：

输入: root = [1,2,3]
输出: [1,3]

提示：

• 二叉树的节点个数的范围是 [0,104]
• -231 <= Node.val <= 231 - 1

算法思路

层序遍历过程中，在执行让下一层节点入队的时候，我们是可以在循环中统计出当前层结点的最大值的。
因此，可以在 bfs 的过程中，统计出每一层结点的最大值。

代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> largestValues(TreeNode* root) {vector<int> ret;if(root == nullptr)return ret;queue<TreeNode*> q;q.push(root);while(!q.empty()){int cur = INT_MIN;int n = q.size();for(int i = 0; i < n; i++){TreeNode* t = q.front();q.pop();cur = max(cur, t->val);if(t->left)q.push(t->left);if(t->right)q.push(t->right);}ret.push_back(cur);}return ret;}
};

⚠️ 写在最后：以上内容是我在学习以后得一些总结和概括，如有错误或者需要补充的地方欢迎各位大佬评论或者私信我交流！！！