NJU 凸优化导论(10) Approximation+Projection逼近与投影的应用（完结撒花）
https://www.lamda.nju.edu.cn/chengq/optfall24/slides/Lecture_10.pdf
目录
Norm Approximation 范数逼近
1. Basic Norm Approximation 基本范数逼近
2. Penalty Function Approximation 罚函数逼近
3. Approximation with Constraints 几种带约束的逼近
Least-norm Problems 最小范数问题
例1. 2-范数
例2. 稀疏解就找1-范数吧
Regularized Approximation 正则化逼近（上两个part的结合）
card ≤ k 的约束 粗暴枚举× 结合正则化√
Projection 投影
例1. 单位正方形与原点
例2. k阶矩阵的投影
凸集上的投影
例1. 不等式约束多面体的 欧几里得投影
例2. 真锥投影
Norm Approximation 范数逼近
1. Basic Norm Approximation 基本范数逼近
也可以理解为Ax=b 在范数下的近似解
如果b属于A的值域 存在Ax=b 最优值就为0 后续还有一些情境上的问题建模解释
1）逼近解释 可看做对A的列向量进行线性组合去逼近b
2）回归估计解释 可看做 y=Ax+v 其中v是未知误差 我们要最小化未知误差
3）几何解释 b到A值域内最近点的距离
4）加权范数的推广 对残差重要程度进行加权
也可以把WA和Wb 作为新的A b 仍然是标准形
5）2-范数 则是最小二乘回归问题
如果是无穷范数 
如果绝对值最大为t 则总体为值为t的向量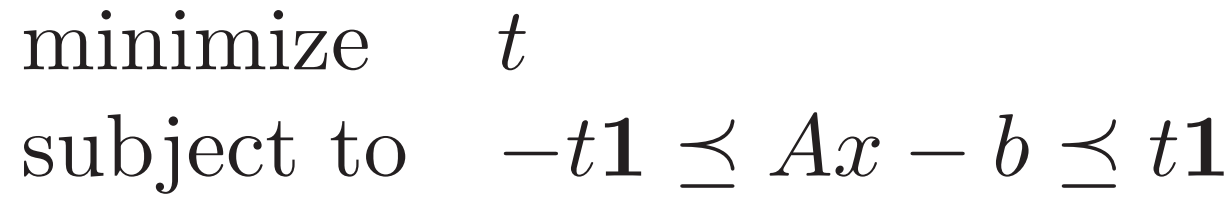 
如果是1-范数 则为
还可以写作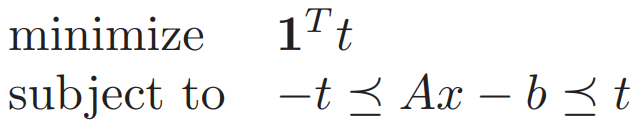
2. Penalty Function Approximation 罚函数逼近
每个残差的影响因子：罚函数φ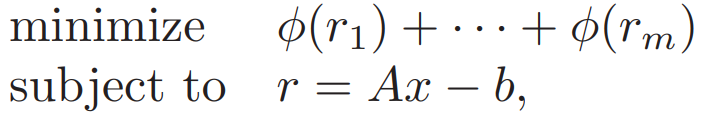 
可延伸出范数形式的罚函数（不管求和外面的1/p次方的话
p可取1 2之类
与阈值范围 [-a,a] 的距离差
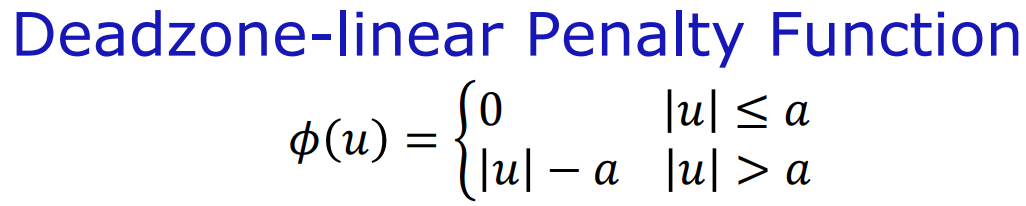
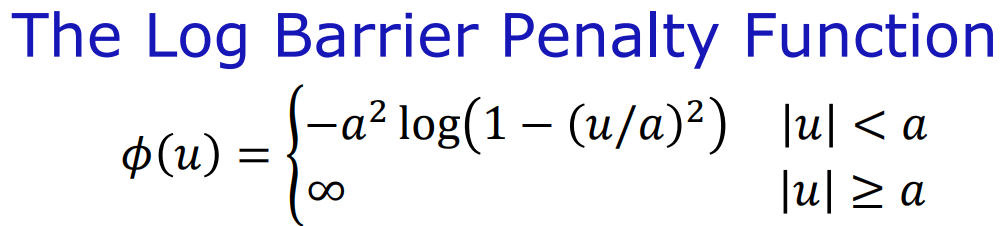
比较这四种罚函数：
- L1范数罚函数对小残差赋予的权重最大，对大残差赋予的权重最小
- 死区-线性对小于阈值的无权重，对大残差赋予的权重也小
- L2范数罚函数对小残差赋予的权重非常小，但对大残差赋予的权重大
- 对数障碍罚函数对小残差赋予的权重与L2范数相似 对比较接近阈值的残差赋予非常大的权重，对>阈值的残差赋予无穷大的权重
3. Approximation with Constraints 几种带约束的逼近
在这个目标的基础上 加上约束
非负约束
盒形上下界
概率分布约束
范数球约束
Least-norm Problems 最小范数问题
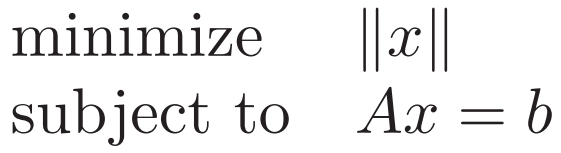标准形式 A的行数m<列数n时 问题才比较有趣
x0 为Ax=b 的一个解 u属于A的零空间 则可以改写为 
（1）测量估计情境：我要测x 先测得一些A和b 但根据这个可以求得多个x；
把范数最小的x 作为最后的估计值
（2）几何解释：
即找仿射集中到0距离最少的点（点0在仿射集上的投影）
例1. 2-范数
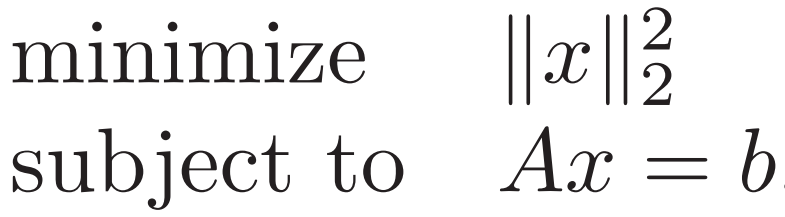代入KKT条件
m<n时 这个逆存在
例2. 稀疏解就找1-范数吧
想得到稀疏解 就把目标函数改成1-范数
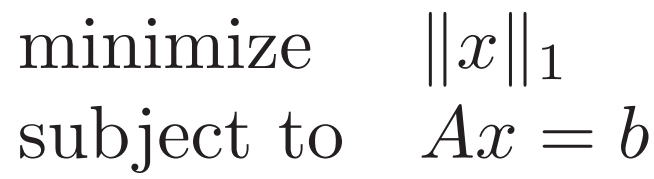
若m<n可对A 变形为m行m列的形式 则会得到一个 只有m个变量是非零元的解
Regularized Approximation 正则化逼近（上两个part的结合）
如果我双目标 也就是逼近效果和 解的范数 两点都需要考虑 则把他们加权都放在目标函数里
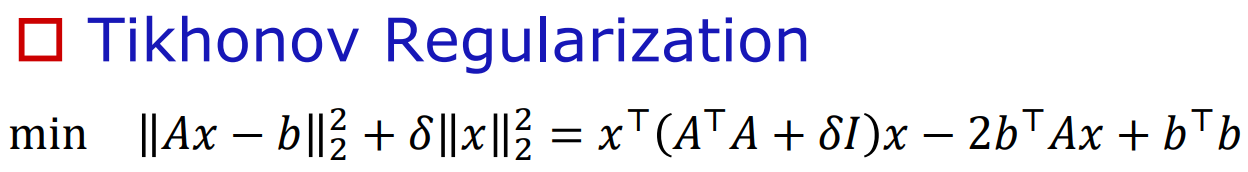
card ≤ k 的约束 粗暴枚举× 结合正则化√
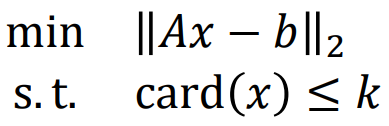如果我要非零元不超过k 只用有限个A的列线性组合
粗暴法：C(n,k) 把所有的选k个都试过去
利用：允许的非零元越多 最优值单调越小
还可通过调整正则化的权重 找一个刚好满足k个非零元的最小的γ （γ越大 惩罚越重 非零元越少）
Projection 投影
x0在C上的投影点为 给定范数下 C中与x0距离最近的那个点
点到集合的距离为 最短距离（即到投影点的距离）
例1. 单位正方形与原点
如果是无穷范数 每个点都是投影点因为距离都最小为1
如果是1或2范数 对应斜正方形和圆 就为坐标轴的那四个点
例2. k阶矩阵的投影
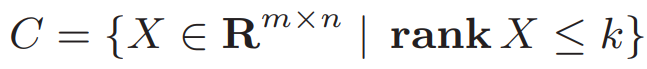
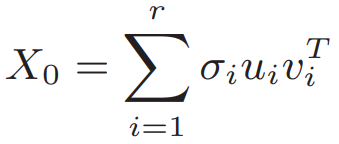如果秩是 r>k 的话 就去掉最小的几个奇异值
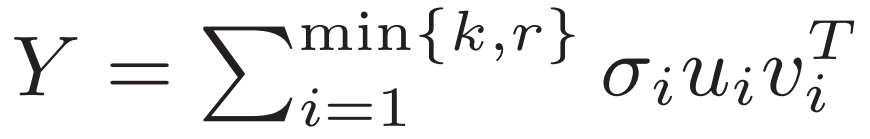
凸集上的投影
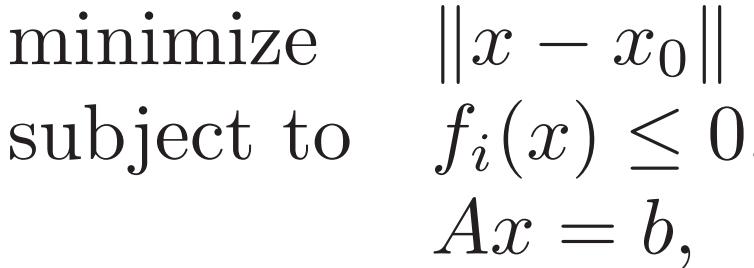即找符合凸集C条件的最近点x
例1. 不等式约束多面体的 欧几里得投影
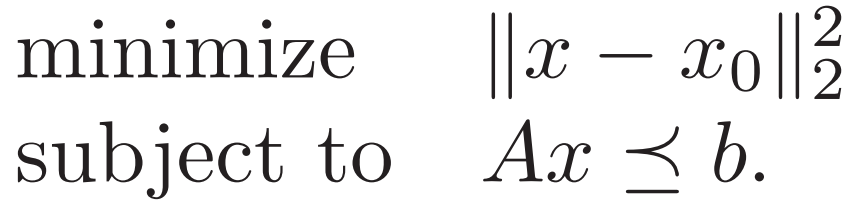
对于超平面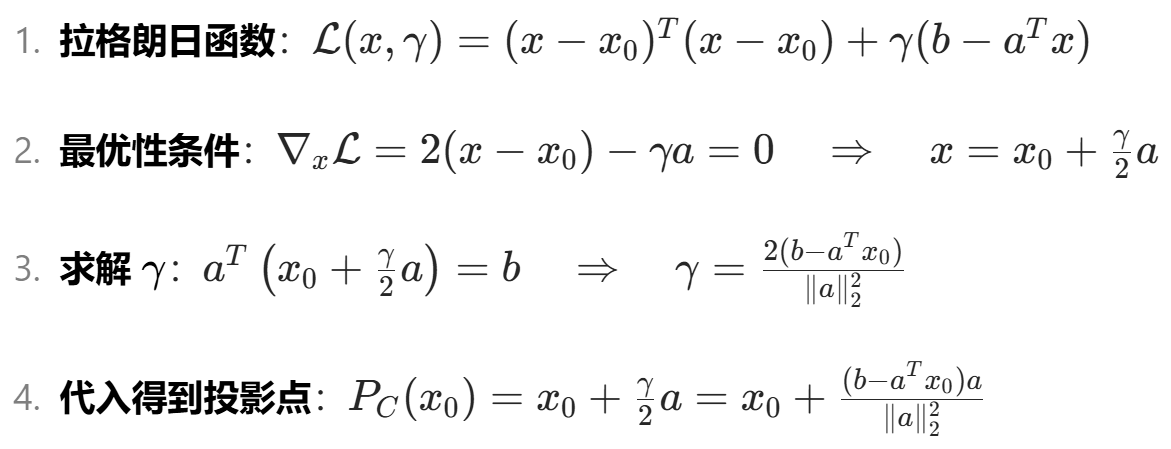
像作垂线的感觉
对于半平面 如果x0在半平面内则就是本身；否则就在超平面上
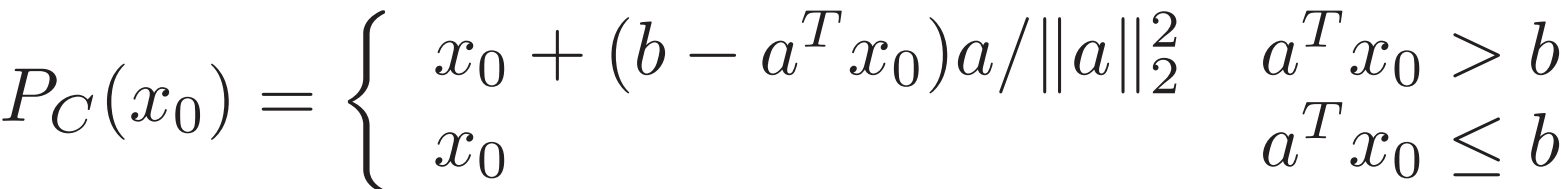
例2. 真锥投影
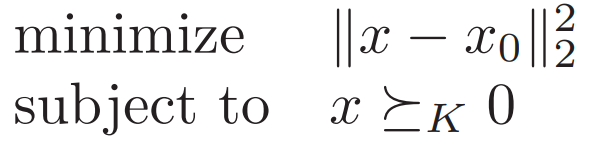
分解为两个正交向量 x0为这两个向量之差 一个在真锥 一个在对偶锥 投影点x为这两个向量之和
若真锥是全正 最近为本身或原点
正特征值处本身 负特征值处0
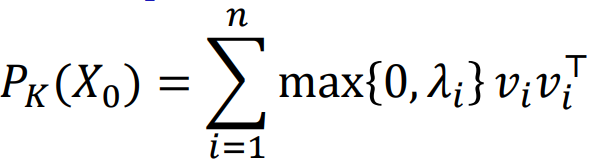
写在最后
南京大学凸优化导论这门课在人工智能学院大二上学期进行。课程主页与使用的经典教材如下。
Introduction to Optimization Methods
Convex Optimization – Boyd and Vandenberghe
从凸集仿射集凸锥这些基本的定义开始，到凸函数、凸优化、对偶、KKT条件。原书后面还有应用、算法两个大板块，还有很多课后习题可以进一步学习。
暑期两周自学看PPT、书本、问AI速通了一下。由于第一次写博客，最开始几篇比较粗糙。
我是南京大学23级工业工程专业学生，对运筹优化方向比较感兴趣，顶礼膜拜呢喃的AI院，凸优化也和运筹学知识比较相关，也是优化领域的重要入门知识，很多AI算法的推导也需要凸优化，遂对着AI院的PPT自学了一下。
希望能帮助到有需要的同学，纯英文的书和PPT难免有些不能一下子理解的地方，我进行了一些简单的解释和总结，祝大家在学习之路更高效更顺利。