暑假训练之动态规划---动态规划的引入

P2842 纸币问题 1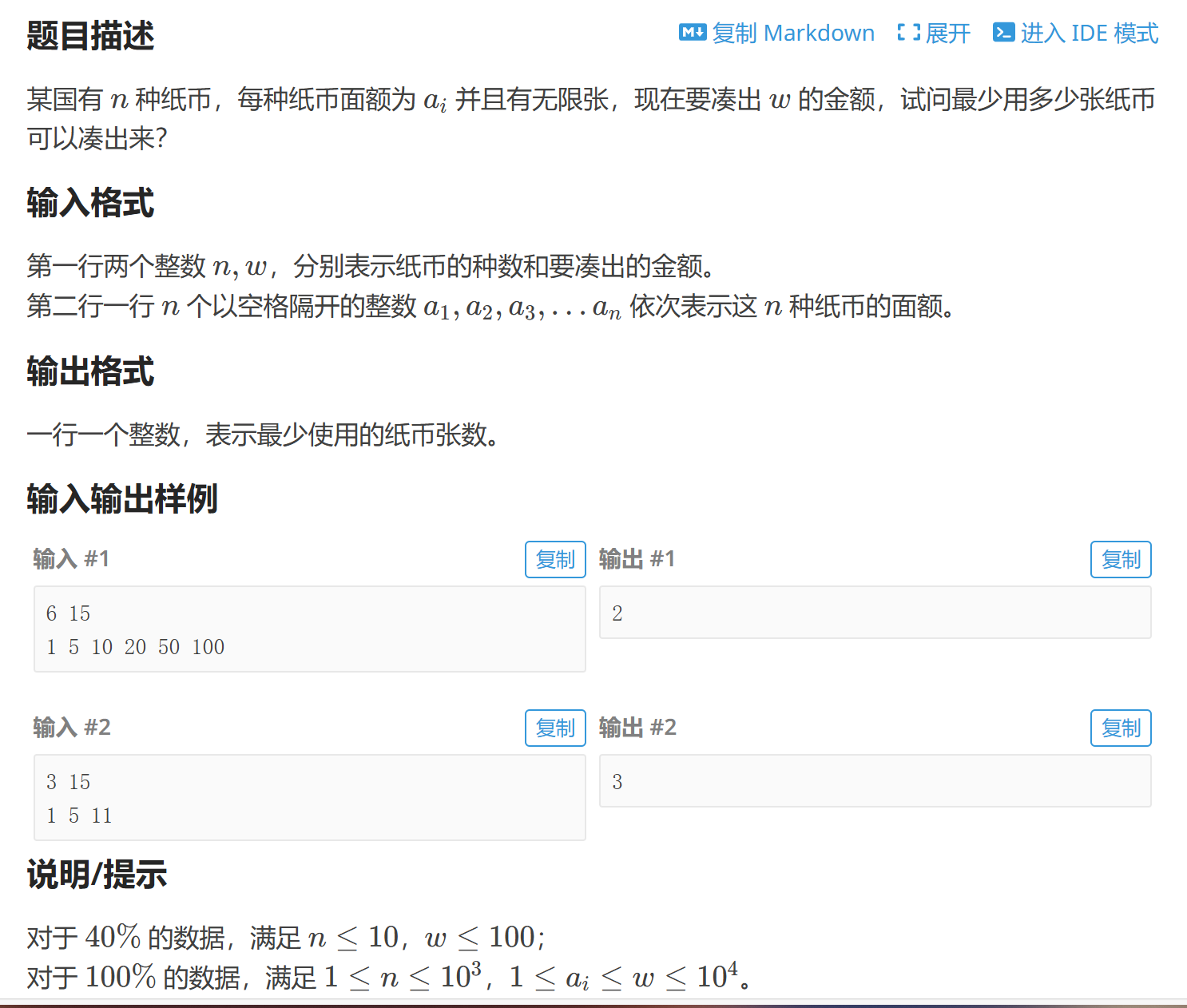

解题思路：

状态：f[i]表示凑出面值为i至少需要的纸币张数

目标态f[w]，初始态f[0]=0,因为凑出0元一张纸币都不要需要

转移方程f[v]=min{f[v-a[i]]}+1

如果v-a[i]需要用x张纸币，那么只需要加上a[i]这一张纸币就行

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
long long n, w, a[10101], f[10010];
void solve()
{cin >> n >> w;for (int i = 1; i <= n; i++)cin >> a[i];for (int i = 1; i <= 10010; i++)f[i] = INT_MAX;for (int i = 1; i <= n; i++)for (int j = a[i]; j <= w; j++)f[j] = min(f[j], f[j - a[i]] + 1);cout << f[w] << endl;
}
signed main()
{int t = 1;// cin>>t;while (t--){solve();}return 0;
}

P1216 [IOI 1994] 数字三角形 Number Triangles

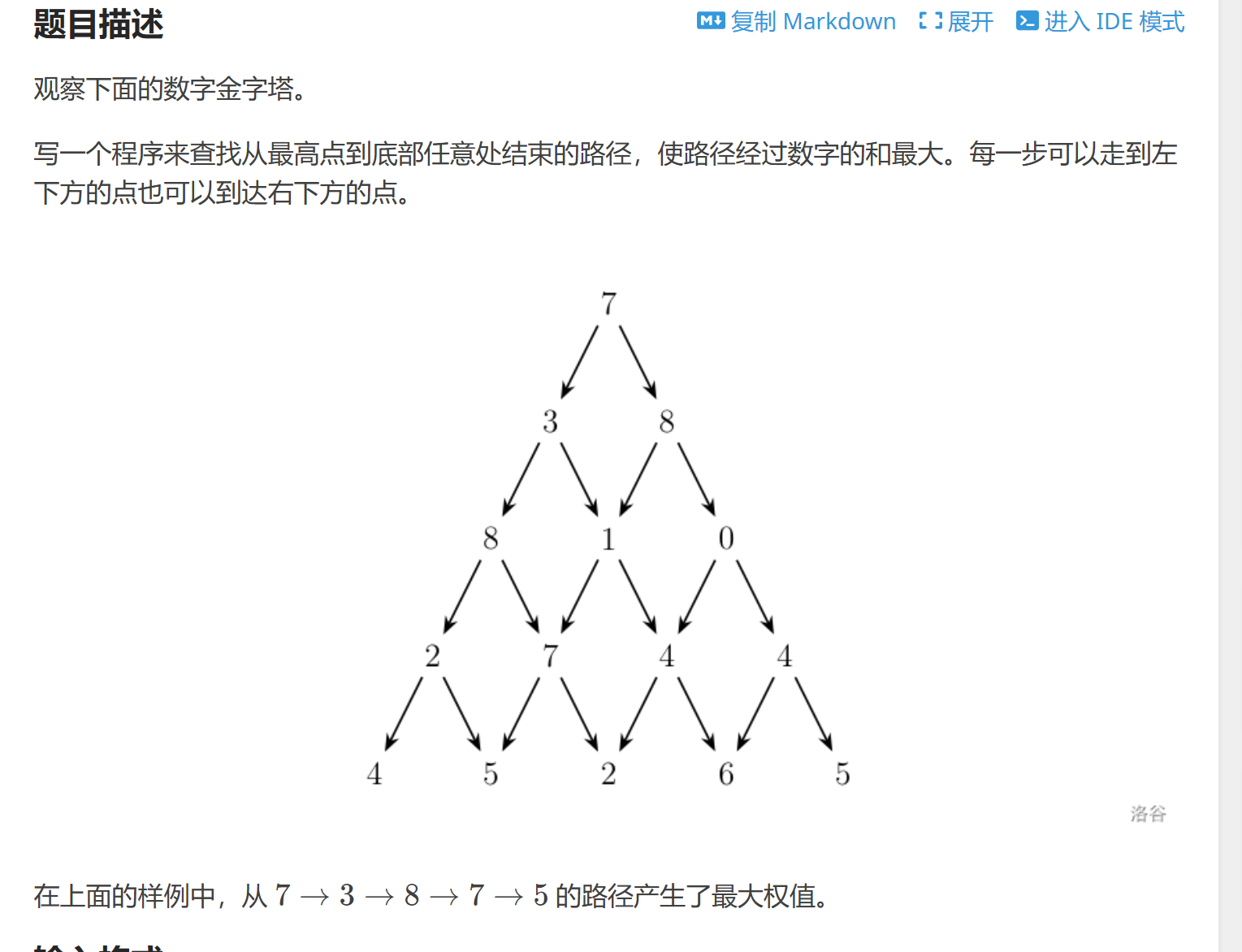
从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
int a[N][N],f[N][N];
void solve()
{int n;cin>>n;for(int i=1;i<=n;i++)for(int j=1;j<=i;j++)cin>>a[i][j];   for(int i=1;i<=n;i++) f[n][i]=a[n][i];for(int i=n-1;i>=1;i--)for(int j=1;j<=i;j++)f[i][j]=max(f[i+1][j]+a[i][j],f[i+1][j+1]+a[i][j]);cout<<f[1][1];
}
signed main()
{int t = 1;// cin>>t;while (t--){solve();}return 0;
}

P2840 纸币问题 2

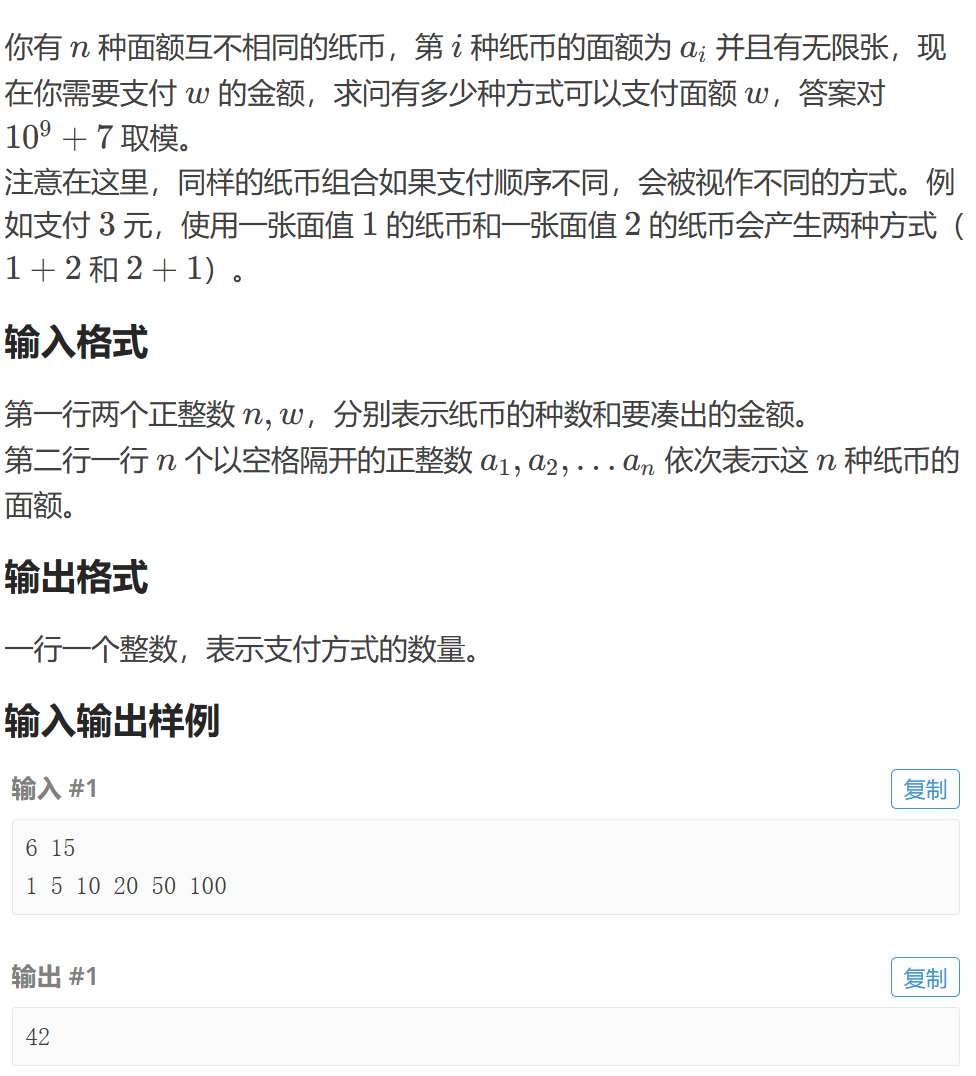
这是一个典型的完全排列型完全背包问题

思路：

1.状态定义：f[i]表示凑出金额i的排列数（支付顺序不太算不同）

2.初始化：f[0]=1表示凑出金额0有一种方法，什么都不选。

3.状态转移：外层遍历金额，内层遍历纸币面额

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
long long n,w,a[N],f[100005];
const int mod=1e9+7;
void solve()
{cin>>n>>w;for(int i=1;i<=n;i++) cin>>a[i];f[0]=1;for(int i=1;i<=w;i++){for(int j=1;j<=n;j++)if(i>=a[j])f[i]=(f[i]+f[i-a[j]])%mod;}cout<<(f[w]%mod);
}
signed main()
{int t = 1;// cin>>t;while (t--){solve();}return 0;
}

P2834 纸币问题 3

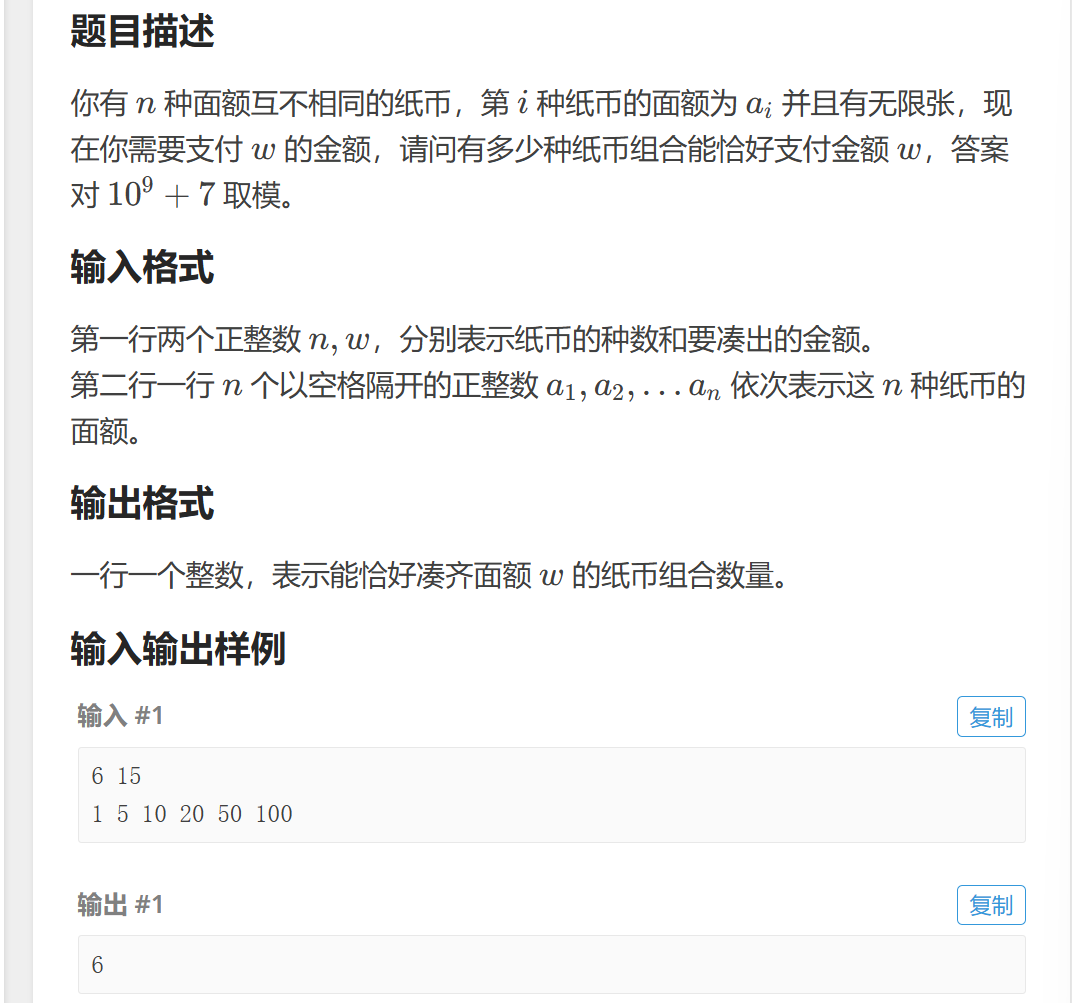
由于是组合计数的问题，需要考虑到纸币种类这个阶段以及每次加入一种新纸币产生的贡献，用fi,j表示只用当前i种纸币凑到金额j的方案数。

于是有了一下两种清空：

1.用了若干张ai，此时前继状态为fi,j-ai

2.没有用一张ai，直接fi-1，j

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
long long n,w,a[N],f[100005];
const int mod=1e9+7;
void solve()
{cin>>n>>w;for(int i=1;i<=n;i++) cin>>a[i];f[0]=1;for(int i=1;i<=n;i++){for(int j=a[i];j<=w;j++){f[j]+=f[j-a[i]]%mod;f[j]%=mod;}}cout<<f[w]<<endl;
}
signed main()
{int t = 1;// cin>>t;while (t--){solve();}return 0;
}

完全背包的板子：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
long long n,w,a[N],f[N][N];
const int mod=1e9+7;
void solve()
{cin>>n>>w;for(int i=1;i<=n;i++) cin>>a[i];f[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=w;j++){f[i][j]=f[i-1][j];if(j>=a[i]) f[i][j]=(f[i][j]+f[i][j-a[i]])%mod;}}cout<<f[n][w]<<endl;
}
signed main()
{int t = 1;// cin>>t;while (t--){solve();}return 0;
}