【数据结构】栈和队列(接口超完整)
文章目录
前言
1、栈(Stack)
1.1、栈的概念和结构
1.2、栈的实现方式及解析
1.3、 栈的实现
1、初始化
2、销毁
3、压栈
4、出栈
5、取栈顶数据
6、获取栈的大小
7、判空
1.4、栈实现完整源码
2、队列(Queue)
2.1、队列的概念和结构
2.2、队列的实现方式解析
2.3、队列的实现
1、队列初始化
2、队列销毁
3、队尾插入(入队列)
4、队头删除(出队列)
5、获取队列大小
6、获取队头数据
7、 获取队尾数据
8、判空
2.4、队列实现完整源码
3、栈和队列比较
前言
栈和队列是计算机科学中两种重要的线性数据结构,均用于存储和管理数据元素。但它们的操作规则和应用场景不同,栈遵循“先进后出”的原则,而队列遵循“先进先出”的原则。
1、栈(Stack)
1.1、栈的概念和结构
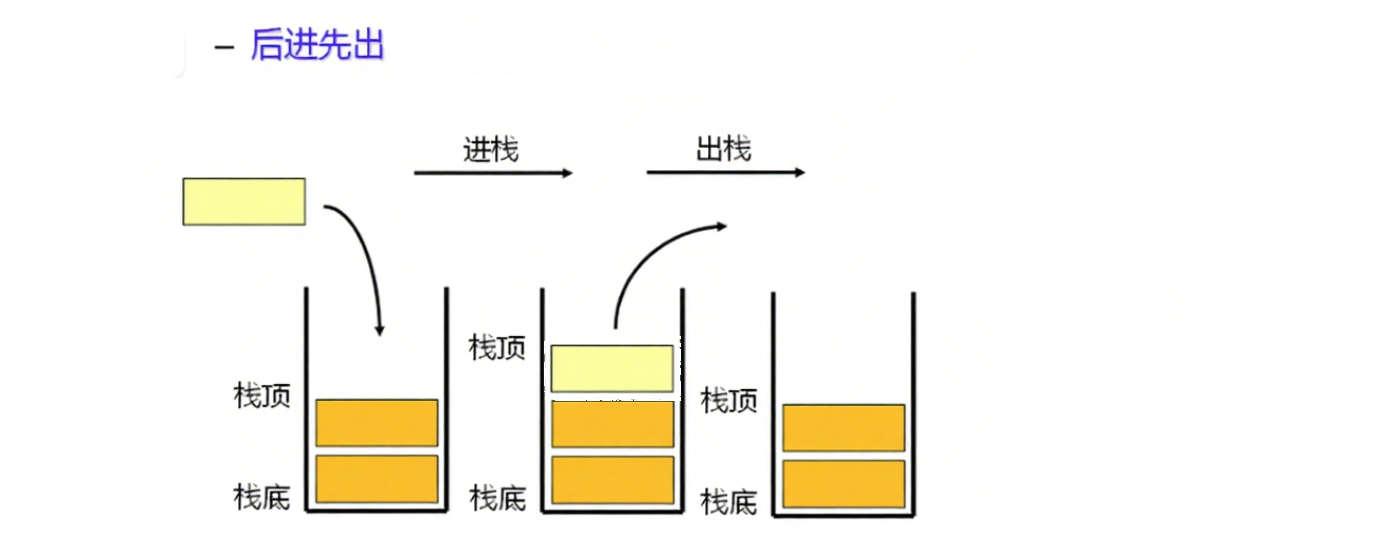
栈是一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
- 栈顶:进行数据的插入和删除的一端;
- 栈底:不允许操作的一端;
基本操作:
- 入栈/压栈(Push):在栈顶添加元素;
- 出栈(Pop):从栈顶移除并返回元素;
- 查看栈顶元素(Peek):返回栈顶元素但不删除;
- 判空(IsEmpty):检查栈中元素是否为空;
- 获取栈的大小(Size):栈中元素个数。

压栈和出栈如下图
1.2、栈的实现方式及解析
栈最重要的就是其先进后出的原则,要实现栈,就要选择能够满足这种原则的方法。
我们发现,其实数组(顺序表),单链表和双向链表都能够用来实现栈。对于数组,压栈可以用realloc来动态扩容,出栈可以直接利用数组的下标;对于单链表,压栈可以用malloc动态申请空间并尾插,出栈只需要找到尾节点然后释放即可;对于双向链表,与单链表相同,只是双向链表可以通过头节点快速找到尾节点。双向链表由于prev指针,所以有额外的空间消费,只是找尾比较方便;相比于单链表,数组在压栈和出栈时,下标就很有优势,代价较小。所以我们选择用数组实现栈。
| 特性 | 数组 | 单链表 |
| 存储空间 | 连续的空间 | 不一定连续 |
| 随机访问 | O(1) | O(N) |
| 压栈 | realloc扩容(成本较高) | malloc动态申请(成本较低) |
| 应用场景 | 元素高效存储+频繁访问 | 任意位置插入和删除频繁 |
| 缓存利用率 | 高 | 低 |
栈主要是对尾部数据进行删除和插入操作,而数组在尾部操作的时间复杂度为O(1),同时,我们可以用二倍扩容来进一步降低扩容成本。
1.3、 栈的实现
我们用多个文件的方式实现,下面先展示头文件,因为头文件包含定义顺序表结构,和实现函数的声明,方便我们的理解。
Stack.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//以顺序表的方式实现栈
typedef int DateType;
//定义顺序表的结构
typedef struct Stack
{DateType* arr; //不定长数组int top; //栈顶位置int capacity; //容量
}ST;//初始化
void STInit(ST* pst);
//销毁
void STDestry(ST* pst);
//压栈
void STPush(ST* pst,DateType x);
//出栈
void STPop(ST* pst);
//取栈顶数据
DateType STTop(ST* pst);
//获取数据个数
int STSize(ST* pst);
//判空
bool STEmpty(ST* pst);1、初始化
初始化时,要特别注意对Top的定义,主要有两种情况:
Top指向栈顶数据,此时,Top应该初始化为-1;

Top指向栈顶数据的下一个位置,此时,Top应该初始化为0;

这里,我们定义Top指向栈顶数据的下一个位置。
//初始化
void STInit(ST* pst)
{assert(pst);pst->arr = NULL;//如果想让栈顶就是最后一个数据,则pst->top应该初始化为 -1 。pst->top = 0;pst->capacity = 0;
}2、销毁
//销毁
void STDestry(ST* pst)
{assert(pst);free(pst->arr);pst->arr = NULL;pst->top = pst->capacity = 0;
}3、压栈
与前面顺序表尾插的思路一致。
//插入数据
void STPush(ST* pst, DateType x)
{assert(pst);//处理空间不足的情况if (pst->top == pst->capacity){//三目操作符处理pst->top为0的情况int newcapacity = pst->top == 0 ? 4 : 2 * pst->capacity;DateType * tmp = realloc(pst->arr, sizeof(DateType) * newcapacity);if (tmp == NULL){perror("realloc");exit(1);}pst->arr = tmp;pst->capacity = newcapacity;}//插入数据pst->arr[pst->top] = x;pst->top++;//pst->arr[pst->top++] = x;
}4、出栈
//删除数据(出栈)
void STPop(ST* pst)
{assert(pst);assert(pst->top > 0);pst->top--;
}5、取栈顶数据
//取栈顶数据
DateType STTop(ST* pst)
{assert(pst);assert(pst->top > 0);return pst->arr[pst->top-1];
}6、获取栈的大小
//获取数据个数
int STSize(ST* pst)
{assert(pst);return pst->top;
}7、判空
当pst->top==0时,返回true,反之返回false。
//判空
bool STEmpty(ST* pst)
{assert(pst);return pst->top == 0;
}1.4、栈实现完整源码
Stack.c(实现代码)
#include"Stack.h"//初始化
void STInit(ST* pst)
{assert(pst);pst->arr = NULL;//pst->top = 0;默认栈顶是在栈的最后一个数据之后,这样也方便插入数据//如果想让栈顶就是最后一个数据,则pst->top应该初始化为 -1 。pst->top = 0;pst->capacity = 0;
}//销毁
void STDestry(ST* pst)
{assert(pst);free(pst->arr);pst->arr = NULL;pst->top = pst->capacity = 0;
}//插入数据
void STPush(ST* pst, DateType x)
{assert(pst);//处理空间不足的情况if (pst->top == pst->capacity){//三目操作符处理pst->top为0的情况int newcapacity = pst->top == 0 ? 4 : 2 * pst->capacity;DateType * tmp = realloc(pst->arr, sizeof(DateType) * newcapacity);if (tmp == NULL){perror("realloc");exit(1);}pst->arr = tmp;pst->capacity = newcapacity;}//插入数据pst->arr[pst->top] = x;pst->top++;//pst->arr[pst->top++] = x;
}//删除数据(出栈)
void STPop(ST* pst)
{assert(pst);assert(pst->top > 0);pst->top--;
}//取栈顶数据
DateType STTop(ST* pst)
{assert(pst);assert(pst->top > 0);return pst->arr[pst->top-1];
}//获取数据个数
int STSize(ST* pst)
{assert(pst);return pst->top;
}//判空
bool STEmpty(ST* pst)
{assert(pst);return pst->top == 0;
}test.c(测试代码)
#include"Stack.h"int main()
{ST s;STInit(&s);//初始化//插入数据STPush(&s, 1);STPush(&s, 2);STPush(&s, 3);STPush(&s, 4);//获取数据个数int num = STSize(&s);printf("%d\n", num);//出栈STPop(&s);STPop(&s);//STPop(&s);//STPop(&s);int temp = s.top;while (temp)//打印{printf("%d->", s.arr[--temp]);}//取栈顶数据DateType ret = STTop(&s);printf("\n%d\n", ret);int x = STSize(&s);printf("%d\n", x);return 0;
}2、队列(Queue)
2.1、队列的概念和结构
队列是只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 FIFO(First In First Out) 原则。进行插入操作的一端称为队尾(入队列 );进行删除操作的一端称为队头(出队列)。
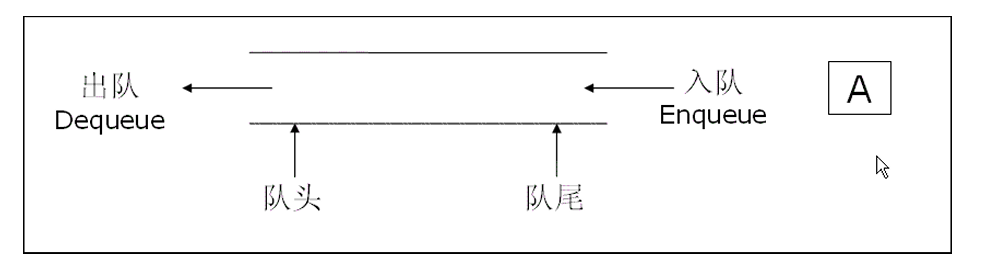
- 基本操作:
- 入队(Enqueue):在队尾添加元素。
- 出队(Dequeue):从队头移除并返回元素。
- 查看队头元素(Front):返回队头元素但不删除。
- 判断队列是否为空(IsEmpty):检查队列中是否没有元素。
- 获取队列的大小(Size):返回队列中元素的数量。
2.2、队列的实现方式解析
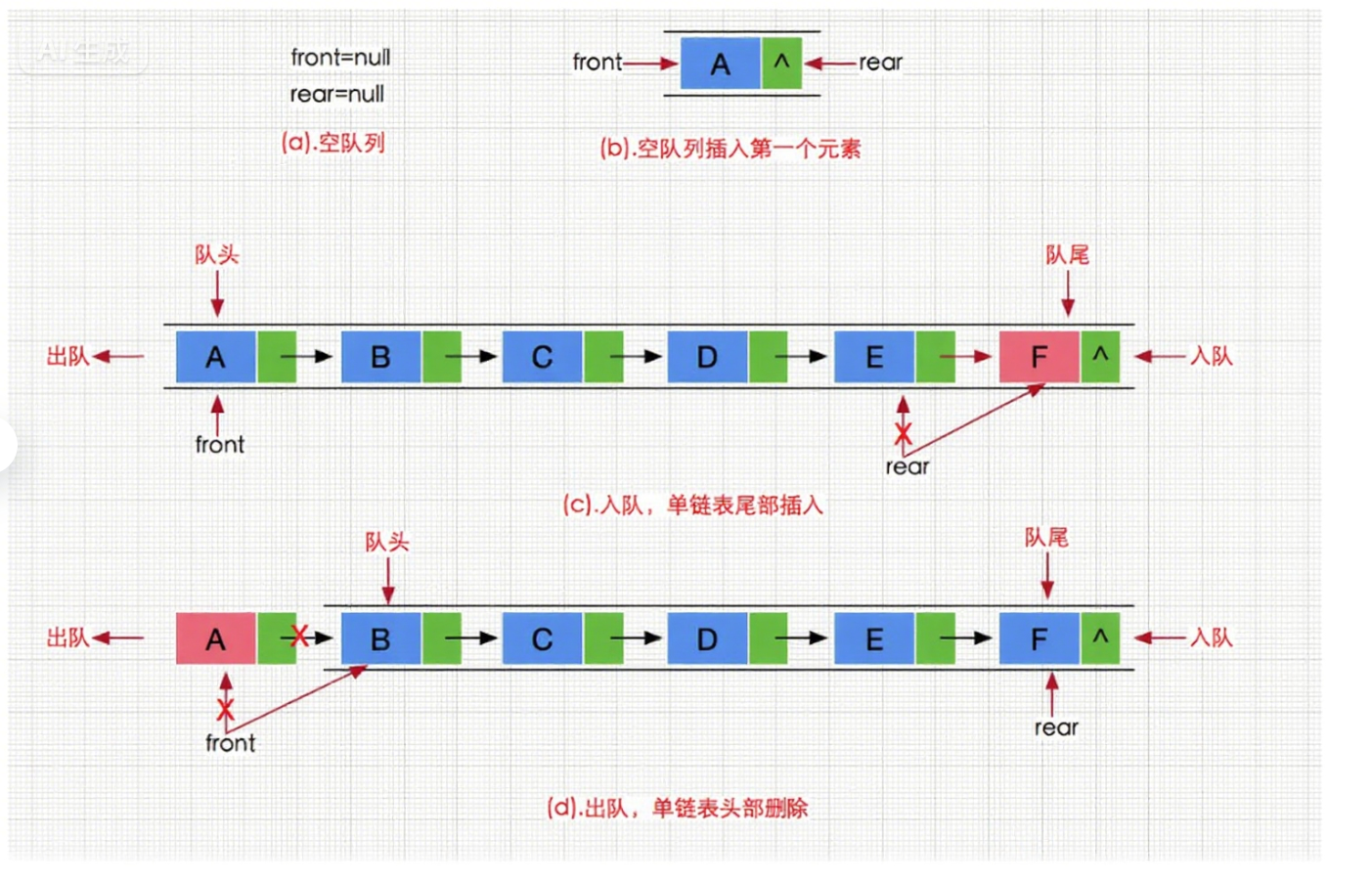
队列的操作原则是先进先出,也可以数组和链表的结构实现。使用链表的结构实现时,尾插和头删即对应入队列和出队列;如果使用数组的结构,出队列在数组头上出数据,需要整体往前移动数组的元素,效率会比较低。所以单链表结构更优
2.3、队列的实现
我们用多个文件的方式实现,部分实现方法与单链表的实现基本一致。下面先展示头文件,因为头文件包含定义队列节点结构,和实现函数的声明,方便我们的理解。
Queue.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int Datetype;
//单链表实现队列
//定义队列节点结构
typedef struct QueueNode
{Datetype val;struct QueueNode* next;
}QNode;//由于队列是先进先出,即在出队列时需要找到队头,插入时需要找到队尾。因此,我们用两个指针来记录队头与队尾
//同时,用size来记录队列的数据个数
typedef struct Queue
{QNode* phead;//指向队头QNode* ptail;//指向队尾int size; //有效数据个数
}Queue;//队列初始化
void QueueInit(Queue* pst);
//队列销毁
void QueueDestry(Queue* pst);
//队尾插入
void QueuePush(Queue* pst, Datetype x);
//队头删除
void QueuePop(Queue* pst);
//获取队列大小
int QueueSize(Queue* pst);
//获取队头数据
Datetype QueueFront(Queue* pst);
//获取队尾数据
Datetype QueueBack(Queue* pst);
//判空
bool QueueEmpty(Queue* pst);1、队列初始化
//队列初始化
void QueueInit(Queue* pst)
{assert(pst);pst->phead = NULL;pst->ptail = NULL;pst->size = 0;
}2、队列销毁
//队列销毁
void QueueDestry(Queue* pst)
{assert(pst);QNode* cur = pst->phead;while (cur){QNode *next= cur->next;free(cur);cur = next;}pst->phead = pst->ptail = NULL;pst->size = 0;
}3、队尾插入(入队列)
//队尾插入
void QueuePush(Queue* pst, Datetype x)
{assert(pst);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc");exit(1);}newnode->val = x;newnode->next = NULL;if (pst->phead == NULL){pst->phead = pst->ptail = newnode;}else{pst->ptail->next = newnode;pst->ptail = newnode;}pst->size++;
}4、队头删除(出队列)
//队头删除
void QueuePop(Queue* pst)
{assert(pst&&pst->ptail);//一个节点if (pst->phead->next == NULL){free(pst->phead);pst->phead = pst->ptail = NULL;}//多个节点else{QNode* next = pst->phead->next;free(pst->phead);pst->phead = next;}pst->size--;
}5、获取队列大小
//获取队列大小
int QueueSize(Queue* pst)
{assert(pst);return pst->size;
}6、获取队头数据
//获取队头数据
Datetype QueueFront(Queue* pst)
{assert(pst);assert(pst->phead);return pst->phead->val;
}7、 获取队尾数据
//获取队尾数据
Datetype QueueBack(Queue* pst)
{assert(pst);assert(pst->ptail);return pst->ptail->val;
}8、判空
//判空
bool QueueEmpty(Queue* pst)
{assert(pst);return pst->ptail == NULL;//return pst->size==0;
}2.4、队列实现完整源码
Queue.c(实现代码)
#include"Queue.h"//队列初始化
void QueueInit(Queue* pst)
{assert(pst);pst->phead = NULL;pst->ptail = NULL;pst->size = 0;
}//队列销毁
void QueueDestry(Queue* pst)
{assert(pst);QNode* cur = pst->phead;while (cur){QNode *next= cur->next;free(cur);cur = next;}pst->phead = pst->ptail = NULL;pst->size = 0;
}//队尾插入
void QueuePush(Queue* pst, Datetype x)
{assert(pst);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc");exit(1);}newnode->val = x;newnode->next = NULL;if (pst->phead == NULL){pst->phead = pst->ptail = newnode;}else{pst->ptail->next = newnode;pst->ptail = newnode;}pst->size++;
}//队头删除
void QueuePop(Queue* pst)
{assert(pst&&pst->ptail);//一个节点if (pst->phead->next == NULL){free(pst->phead);pst->phead = pst->ptail = NULL;}//多个节点else{QNode* next = pst->phead->next;free(pst->phead);pst->phead = next;}pst->size--;
}//获取队列大小
int QueueSize(Queue* pst)
{assert(pst);return pst->size;
}//获取队头数据
Datetype QueueFront(Queue* pst)
{assert(pst);assert(pst->phead);return pst->phead->val;
}//获取队尾数据
Datetype QueueBack(Queue* pst)
{assert(pst);assert(pst->ptail);return pst->ptail->val;
}//判空
bool QueueEmpty(Queue* pst)
{assert(pst);return pst->ptail == NULL;//return pst->size==0;
}test.c(测试代码)
#include"Queue.h"int main()
{Queue pq;QueueInit(&pq);//初始化//队尾插入QueuePush(&pq, 1);QueuePush(&pq, 2);QueuePush(&pq, 3);QueuePush(&pq, 4);////队头删除//QueuePop(&pq);QNode* ps = pq.phead;while (ps){printf("%d->", ps->val);ps = ps->next;}////取队列数据个数//int num = QueueSize(&pq);//printf("\n%d\n", num);////获取队头数据//Datetype Front = QueueFront(&pq);//printf("\n%d\n", Front);////获取队尾数据//Datetype Back = QueueBack(&pq);//printf("\n%d\n", Back);////判空//bool flag = QueueEmpty(&pq);//if (flag)// printf("\n空\n");//else// printf("\n非空\n");//销毁QueueDestry(&pq);return 0;
}3、栈和队列比较
| 特性 | 栈(Stack) | 队列(Queue) |
| 操作端 | 仅栈顶允许插入和删除 | 队尾插入,队头删除 |
| 原则 | 后进先出(LIFO) | 先进先出(FIFO) |
| 典型应用 | 递归、括号匹配、表达式求值 | 任务调度、BFS、消息队列 |
