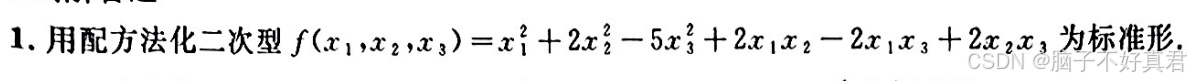一文速通《二次型》

一、必须记住解题所用结论

(1) 矩阵可相似对角化的充要条件是有 n 个线性无关的特征向量（即对应特征值的几何重数等于相应的代数重数）.

(1.1) 矩阵可相似对角化​​的充分条件是矩阵的特征值全为单值（即“特征值全为单值” ⟹ “矩阵可对角化”）.

(2) 矩阵可正交对角化的充要条件是它是实对称矩阵（即实对称矩阵一定可以正交对角化）.

(3) 两个矩阵等价的充要条件是它们具有相同的秩.

(4) A与B等价，即存在可逆矩阵P和Q使得PAQ=B.

(5) 矩阵无论是左乘、右乘还是同时左右乘以可逆矩阵，其秩不变.

(6) 二次型的标准型不唯一，但规范性唯一（比如配方法和正交变换法求得的标准型就不一样）.

(7) 只有通过正交变换法得到的标准型的主对角线元素才是原矩阵的特征值，而通过配方法得到的标准型的主对角线元素通常不是原矩阵的特征值.

(8) 矩阵（首先矩阵必须是实对称矩阵）正定的充要条件是（判断矩阵是否正定的条件，满足其一即可）：
①矩阵所有特征值均为正数（不能为0，如果说无负特征值就是错的）.
或②矩阵所有顺序子式（即从左上角开始的各阶子矩阵的行列式）均大于零.

(9)一个实对称矩阵 A通过合同变换（即 A→(P^T)AP，其中 P可逆）化为的对角矩阵(标准型)后其​​正、负、零元素个数​​是唯一的.
正惯性指数：标准型中正系数的个数，通常记为 p。
负惯性指数：标准型中负系数的个数，通常记为 q。

(10) 两个齐次线性方程组 Ax = 0 和 Bx = 0 同解的充要条件是：它们的系数矩阵 A 和 B 行等价.
行等价：如果矩阵 B 可以通过对矩阵 A 进行有限次初等行变换得到，那么 A 和 B 就是行等价的。

(11) 两个实对称矩阵合同的充要条件是它们有相同的正负惯性指数（正负惯性指数即合同对角化后的对角矩阵主对角线元素，即正特征值个数与负特征值个数）. 

(12) 实对称矩阵的秩=其非零特征值的个数.

(13) 实对称矩阵的不同特征值对应的特征向量相互正交.

(14) 实对称矩阵一定可以对角化.

二、配方法化二次型为标准型

(1) 步骤

第一步：选择一个变量并凑成完全平方

第二步：分离出平方项和剩余部分

第三步：对剩余部分重复以上步骤

(2) 例题

三、正交变换将二次型化为标准型

(1) 步骤

第一步：写出二次型的实对称矩阵 A.

第二步：求出矩阵 A 的所有特征值.

第三步：求出每个特征值对应的特征向量.

第四步：将特征向量正交化、单位化.

第五步：构造正交矩阵 Q 并写出结论.

(2) 例题

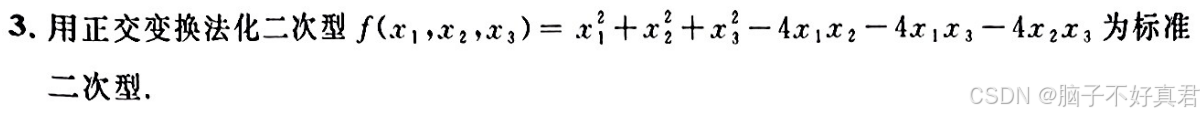
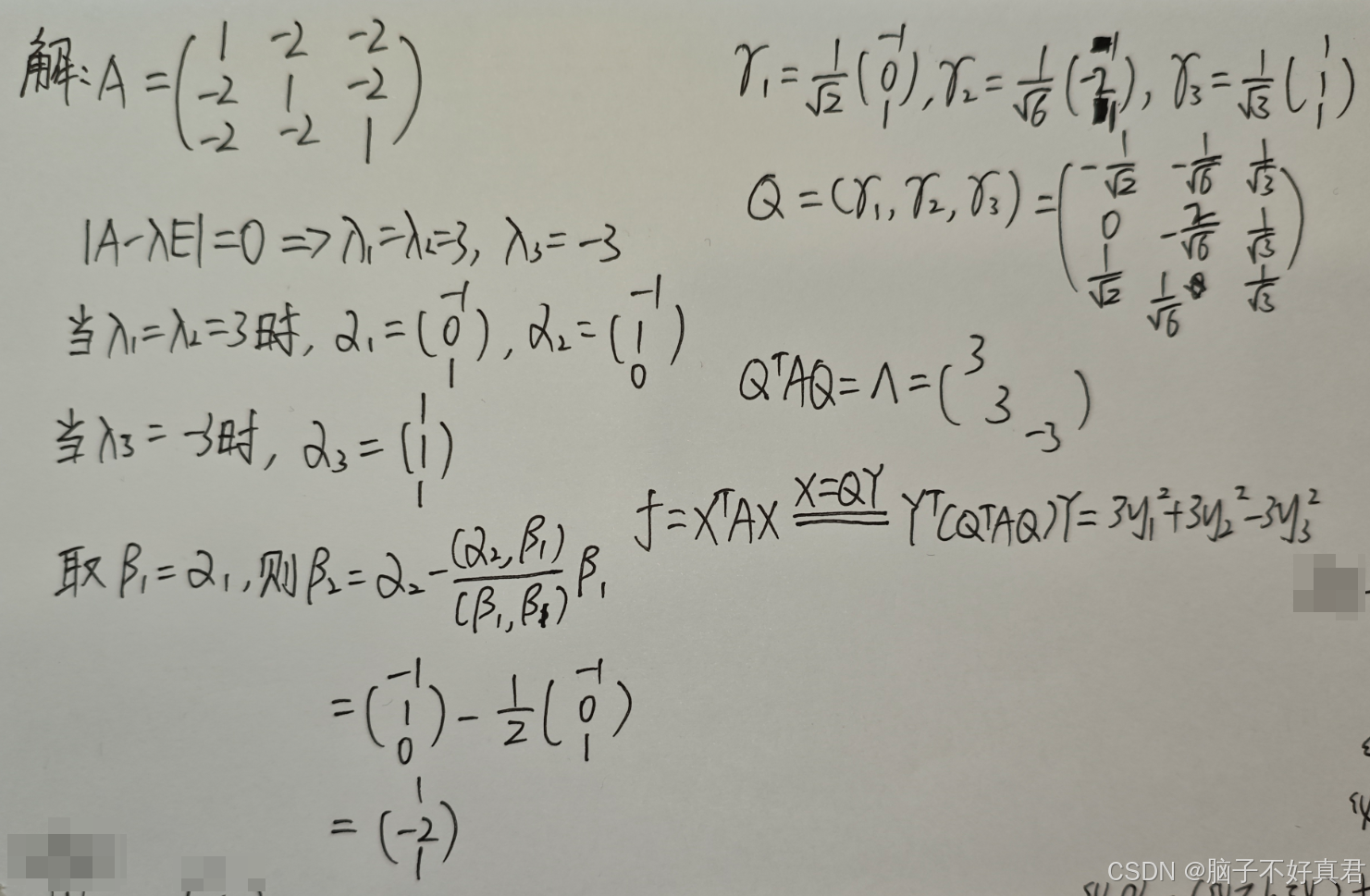
四、施密特正交化