《P2680 [NOIP 2015 提高组] 运输计划》

题目背景

NOIP2015 Day2T3

题目描述

公元 2044 年，人类进入了宇宙纪元。

L 国有 n 个星球，还有 n−1 条双向航道，每条航道建立在两个星球之间，这 n−1 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司， 该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 ui​ 号星球沿最快的宇航路径飞行到 vi​ 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 j，任意飞船驶过它所花费的时间为 tj​，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后，这 m 个运输计划会同时开始，所有飞船一起出发。当这 m 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞， 试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入格式

第一行包括两个正整数 n,m，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 1 到 n 编号。

接下来 n−1 行描述航道的建设情况，其中第 i 行包含三个整数 ai​,bi​ 和 ti​，表示第 i 条双向航道修建在 ai​ 与 bi​ 两个星球之间，任意飞船驶过它所花费的时间为 ti​。

接下来 m 行描述运输计划的情况，其中第 j 行包含两个正整数 uj​ 和 vj​，表示第 j 个运输计划是从 uj​ 号星球飞往 vj​号星球。

输出格式

一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入 #1复制

6 3 
1 2 3 
1 6 4 
3 1 7 
4 3 6 
3 5 5 
3 6 
2 5 
4 5

输出 #1复制

11

说明/提示

所有测试数据的范围和特点如下表所示

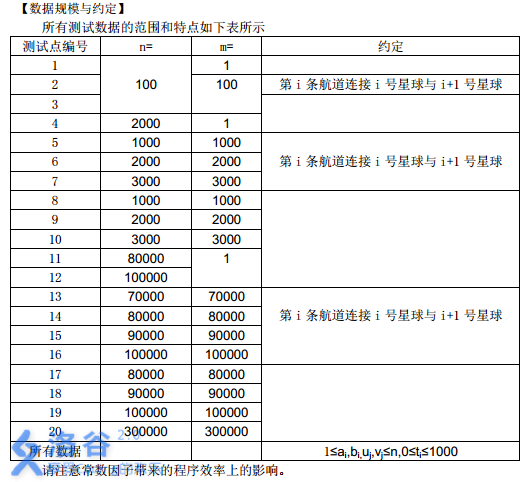
请注意常数因子带来的程序效率上的影响。

对于 100% 的数据，保证：1≤ai​,bi​≤n，0≤ti​≤1000，1≤ui​,vi​≤n。

代码实现：

#include<bits/stdc++.h>
#define int long long
using namespace std;
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)

const int MAXN = 300005;

int planetCount, planCount, maxPlanLength;

struct Edge {
int to;
int weight;
};

vector<Edge> adj[MAXN];  // 邻接表存储树结构
int ancestor[MAXN][30];  // 倍增法LCA祖先数组
int logTable[MAXN];      // logTable[i] = log2(i)
int nodeDepth[MAXN];     // 节点深度
int nodeDistance[MAXN];  // 根到节点的距离
int diffCount[MAXN];     // 差分数组
int planLCA[MAXN];       // 每个运输计划的LCA
int planDistance[MAXN];  // 每个运输计划的路径长度

struct TransportPlan {
int start;
int end;
};

TransportPlan plans[MAXN];  // 存储所有运输计划

// 预处理DFS：计算深度、距离和直接父节点
void preprocessDFS(int currentNode, int parentNode) {
nodeDepth[currentNode] = nodeDepth[parentNode] + 1;
ancestor[currentNode][0] = parentNode;

for (Edge edge : adj[currentNode]) {
int neighborNode = edge.to;
if (neighborNode == parentNode) continue;
nodeDistance[neighborNode] = nodeDistance[currentNode] + edge.weight;
preprocessDFS(neighborNode, currentNode);
}
}

// 计算两个节点的最近公共祖先
int findLCA(int nodeA, int nodeB) {
if (nodeDepth[nodeA] < nodeDepth[nodeB]) swap(nodeA, nodeB);

// 将nodeA提升到与nodeB相同深度
while (nodeDepth[nodeA] > nodeDepth[nodeB]) {
nodeA = ancestor[nodeA][logTable[nodeDepth[nodeA] - nodeDepth[nodeB]]];
}

if (nodeA == nodeB) return nodeA;

// 同时向上跳跃，找到LCA
for (int i = logTable[nodeDepth[nodeA]]; i >= 0; i--) {
if (ancestor[nodeA][i] != ancestor[nodeB][i]) {
nodeA = ancestor[nodeA][i];
nodeB = ancestor[nodeB][i];
}
}

return ancestor[nodeA][0];
}

// 树上差分还原：计算每条边被覆盖的次数
void dfsForDiff(int currentNode, int parentNode) {
for (Edge edge : adj[currentNode]) {
int neighborNode = edge.to;
if (neighborNode == parentNode) continue;
dfsForDiff(neighborNode, currentNode);
diffCount[currentNode] += diffCount[neighborNode];
}
}

// 二分法检查是否存在可行的改造方案
bool checkFeasible(int candidateTime) {
memset(diffCount, 0, sizeof(diffCount));
int countExceed = 0;
int maxExceedLength = 0;

// 找出所有超过候选时间的路径，进行差分标记
for (int i = 1; i <= planCount; i++) {
if (planDistance[i] > candidateTime) {
diffCount[plans[i].start]++;
diffCount[plans[i].end]++;
diffCount[planLCA[i]] -= 2;
countExceed++;
}
maxExceedLength = max(maxExceedLength, planDistance[i]);
}

// 如果没有超过的路径，直接返回可行
if (countExceed == 0) return true;

// 还原差分数组，计算每条边的覆盖次数
dfsForDiff(1, 0);

// 检查是否存在一条边，满足所有超过的路径都经过它，并且改造后总时间不超过候选时间
for (int i = 2; i <= planetCount; i++) {
if (diffCount[i] == countExceed) {
int edgeWeight = nodeDistance[i] - nodeDistance[ancestor[i][0]];
if (maxExceedLength - edgeWeight <= candidateTime) {
return true;
}
}
}

return false;
}

signed main() {
scanf("%lld%lld", &planetCount, &planCount);
int binarySearchLeft = 0, binarySearchRight = 0, mid;

// 预处理log表
for (int i = 2; i <= planetCount; i++) {
logTable[i] = logTable[i >> 1] + 1;
}

// 读取星球间的航道信息
for (int i = 1; i < planetCount; i++) {
int planetA, planetB, travelTime;
scanf("%lld%lld%lld", &planetA, &planetB, &travelTime);
adj[planetA].push_back({planetB, travelTime});
adj[planetB].push_back({planetA, travelTime});
binarySearchLeft = max(binarySearchLeft, travelTime);
}

// 预处理DFS
preprocessDFS(1, 0);

// 预处理倍增数组
for (int i = 1; i <= logTable[planetCount]; i++) {
for (int j = 1; j <= planetCount; j++) {
ancestor[j][i] = ancestor[ancestor[j][i-1]][i-1];
}
}

// 处理每个运输计划，计算路径长度和LCA
for (int i = 1; i <= planCount; i++) {
scanf("%lld%lld", &plans[i].start, &plans[i].end);
planLCA[i] = findLCA(plans[i].start, plans[i].end);
planDistance[i] = nodeDistance[plans[i].start] + nodeDistance[plans[i].end] - 2 * nodeDistance[planLCA[i]];
binarySearchRight = max(binarySearchRight, planDistance[i]);
}

maxPlanLength = binarySearchRight;
binarySearchLeft = binarySearchRight - binarySearchLeft;

// 二分查找最小可行时间
while (binarySearchLeft < binarySearchRight) {
mid = (binarySearchLeft + binarySearchRight) >> 1;
if (checkFeasible(mid)) {
binarySearchRight = mid;
} else {
binarySearchLeft = mid + 1;
}
}

cout << binarySearchRight;
return 0;
}