【每日算法】专题十五_BFS 解决 FloodFill 算法

1. 算法思想

Flood Fill 问题的核心需求

给定一个二维网格（如像素矩阵）、一个起始坐标 (x, y) 和目标颜色 newColor，要求：

1. 将起始点 (x, y) 的颜色替换为 newColor。
2. 递归地将所有与起始点相邻（上下左右） 且颜色与起始点原始颜色相同的区域，也替换为 newColor。

BFS 解决 Flood Fill 的算法思想

BFS 通过队列实现 “逐层扩散”，步骤如下：

1. 记录原始颜色，处理边界情况

• 首先获取起始点 (x, y) 的原始颜色 oldColor。
• 若 oldColor 与 newColor 相同，直接返回（无需填充，避免死循环）。

2. 初始化队列，标记起始点

• 将起始点 (x, y) 加入队列，作为 BFS 的起点。
• 立即将起始点的颜色更新为 newColor（或通过访问标记记录已处理，避免重复处理）。

3. 逐层扩散，填充相邻区域

• 循环取出队列中的节点 (x, y)，检查其上下左右四个相邻节点：
  • 若相邻节点在网格范围内（未越界）。
  • 且相邻节点的颜色为 oldColor（与起始点原始颜色相同）。
• 则将该相邻节点加入队列，并立即更新其颜色为 newColor（或标记为已处理）。

4. 队列清空，完成填充

• 当队列中所有节点都处理完毕后，所有与起始点连通的 oldColor 区域已被替换为 newColor，算法结束。

示例：图像着色（Flood Fill 经典场景）

假设有如下像素网格（oldColor=1，newColor=2，起始点 (1, 1)）：

[[1, 1, 0],[1, 1, 0],[0, 0, 1]
]

BFS 执行过程：

1. 起始点 (1,1) 入队，颜色更新为 2，队列：[(1,1)]。
2. 取出 (1,1)，检查四邻：
   • (0,1) 是 1 → 入队，更新为 2；队列：[(0,1)]。
   • (2,1) 是 0 → 跳过。
   • (1,0) 是 1 → 入队，更新为 2；队列：[(0,1), (1,0)]。
   • (1,2) 是 0 → 跳过。
3. 取出 (0,1)，检查四邻：
   • (0,0) 是 1 → 入队，更新为 2；队列：[(1,0), (0,0)]。
   • 其他邻点已处理或颜色不符，跳过。
4. 取出 (1,0) 和 (0,0)，检查其邻点，均无未处理的 1，队列清空。
5. 最终结果（所有连通的 1 均变为 2）：

[[2, 2, 0],[2, 2, 0],[0, 0, 1]
]

关键逻辑解析

• 为什么用 BFS？：BFS 按 “距离起始点由近及远” 的顺序填充，适合需要 “逐层扩散” 的场景，且能保证所有连通区域被完整覆盖。
• 避免重复处理：通过 “立即更新颜色为 newColor” 替代单独的访问标记数组，节省空间（因为 oldColor != newColor，已处理节点不会被再次加入队列）。
• 边界检查：每次访问邻点前需判断 x 和 y 是否在网格范围内（0 ≤ x < 行数，0 ≤ y < 列数）。

算法复杂度

• 时间复杂度：O(n*m)，其中 n 为网格行数，m 为列数。每个单元格最多被访问一次。
• 空间复杂度：O(n*m)，最坏情况下队列需存储所有单元格（如整个网格都是 oldColor 时）。

总结

BFS 解决 Flood Fill 的核心是用队列管理待处理节点，逐层扩散并实时更新颜色，确保所有与起始点连通的相同颜色区域被高效、完整地填充。该思路直观且易于实现，是处理连通区域填充问题的首选方法之一。

2. 例题

2.1 图像渲染

733. 图像渲染 - 力扣（LeetCode）

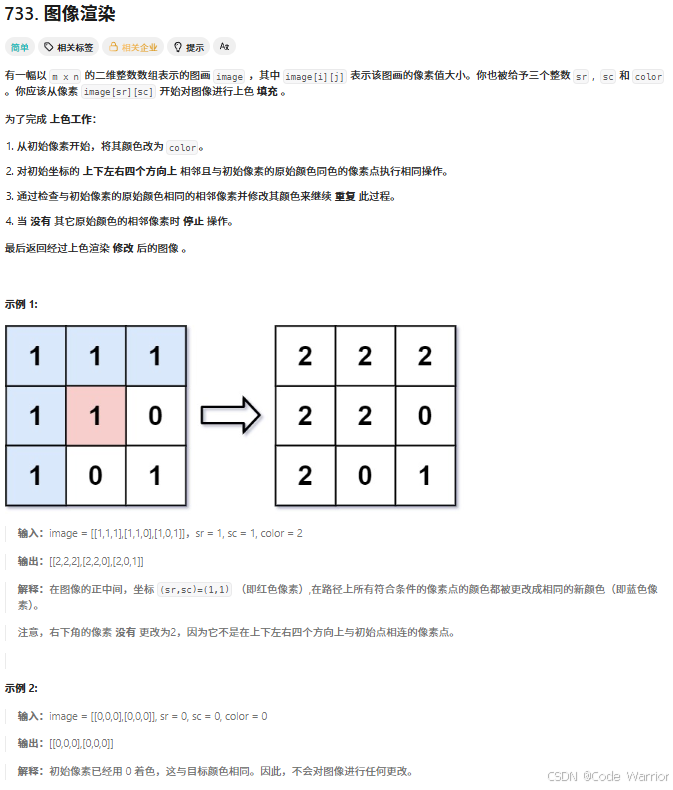
核心思路

1. 颜色检查与预处理：

   • 获取起始点 (sr, sc) 的原始颜色 prev。
   • 若 prev 与目标颜色 color 相同，直接返回原图（避免重复填充）。

2. BFS 初始化：

   • 将起始点 (sr, sc) 加入队列 q。
   • 获取图像的行数 n 和列数 m，用于边界检查。

3. 逐层扩散填充：

   • 循环处理队列中的每个点，将其颜色替换为 color。
   • 检查该点的上下左右四个相邻点：
     • 若相邻点在图像范围内且颜色等于 prev，将其加入队列。
   • 队列处理完毕后，所有连通的 prev 颜色区域均被替换为 color。

关键逻辑解析

1. 为什么用 BFS？
   BFS 按 “距离起始点由近及远” 的顺序处理节点，确保所有连通区域被完整覆盖，且避免重复访问。

2. 如何避免重复处理？
   当一个点被加入队列时，立即将其颜色更新为 color。后续检查相邻点时，由于 image[x][y] == prev 的条件，已处理的点（颜色已变为 color）不会被重复加入队列。

3. 边界检查的重要性
   x >= 0 && x < n && y >= 0 && y < m 确保不会越界访问图像。

示例演示

原图（prev=1，color=2，起始点 (1, 1)）：

[[1, 1, 0],[1, 1, 0],[0, 0, 1]
]

BFS 执行过程：

1. 起始点 (1,1) 入队，颜色更新为 2，队列：[(1,1)]。
2. 处理 (1,1)，检查四邻：
   • (0,1) 颜色为 1 → 入队，更新为 2。
   • (1,0) 颜色为 1 → 入队，更新为 2。
   • 其他邻点颜色为 0 或越界，跳过。
3. 处理 (0,1)，检查四邻：
   • (0,0) 颜色为 1 → 入队，更新为 2。
4. 处理 (1,0) 和 (0,0)，无符合条件的邻点。
5. 队列为空，处理结束，结果：

[[2, 2, 0],[2, 2, 0],[0, 0, 1]
]

复杂度分析

• 时间复杂度：O(n*m)，其中 n 和 m 分别为图像的行数和列数。每个像素最多被访问一次。
• 空间复杂度：O(n*m)，最坏情况下队列可能存储所有像素（如整个图像颜色相同）。

总结

该算法通过 BFS 高效地实现了 Flood Fill，核心在于利用队列逐层扩散并实时更新颜色以避免重复处理。这种方法简洁直观，适用于处理图像连通区域的填充问题。

 

class Solution {// 表示x和y坐标typedef pair<int, int> PII;// 上下左右四个方向的偏移量int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};public:vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {int prev = image[sr][sc];if(prev == color) return image;queue<PII> q;q.push({sr, sc});int n = image.size(), m = image[0].size();while(q.size()){auto [x1, y1] = q.front();q.pop();image[x1][y1] = color; for(int i = 0; i < 4; ++i){int x = x1 + dx[i], y = y1 + dy[i];// 找到四个方向符合条件的位置if(x >= 0 && x < n && y >= 0 && y < m && image[x][y] == prev){q.push({x, y}); }}}return image;}
};

 

2.2 岛屿数量

200. 岛屿数量 - 力扣（LeetCode）

 

核心思路

1. 遍历网格，寻找未访问的陆地
   遍历二维网格的每个单元格，当遇到值为 '1'（表示陆地）且未被访问过（!vis[i][j]）的单元格时，说明发现了一个新的岛屿。

2. BFS 扩散标记整个岛屿
   对每个新发现的陆地单元格，启动 BFS：

   • 将该单元格加入队列，作为 BFS 的起点。
   • 从队列中取出单元格，检查其上下左右四个相邻单元格：
     • 若相邻单元格在网格范围内（未越界）、值为 '1' 且未被访问过，则将其加入队列，并标记为已访问（vis[x][y] = true）。
   • 此过程会递归遍历完当前岛屿的所有相连陆地，确保整个岛屿被完整标记。

3. 计数岛屿数量
   每启动一次 BFS，代表发现并处理了一个完整的岛屿，因此计数器（ret）加 1。最终计数器的值即为网格中岛屿的总数量。

关键逻辑解析

• vis 数组的作用：记录已访问的陆地单元格，避免重复统计同一岛屿的单元格。
• BFS 的优势：通过队列实现 “逐层扩散”，确保所有与起始点连通的陆地都被标记，高效覆盖整个岛屿。
• 边界检查：通过 x >= 0 && x < n && y >= 0 && y < m 确保不访问网格外的无效区域。

总结

算法通过遍历网格发现新岛屿，利用 BFS 标记整个岛屿的所有陆地，最终统计岛屿数量。核心是用 BFS 实现连通区域的完整覆盖和用访问标记避免重复统计，时间复杂度为 O(n*m)（n、m 为网格行列数），每个单元格最多被访问一次。

class Solution {typedef pair<int, int> PII;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int n, m;bool vis[300][300];public:int numIslands(vector<vector<char>>& grid) {int ret = 0;n = grid.size(), m = grid[0].size();for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){if(grid[i][j] == '1' && !vis[i][j]){++ret;dfs(grid, i, j);}}}return ret;}void dfs(vector<vector<char>>& grid, int i, int j){queue<PII> q;q.push({i, j});while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] == '1' && !vis[x][y]){q.push({x, y});vis[x][y] = true; }}}}
};

 

2.3 岛屿的最大面积

695. 岛屿的最大面积 - 力扣（LeetCode）

核心思路

1. 遍历网格，寻找未访问的陆地
   遍历二维网格的每个单元格，当遇到值为 1（表示陆地）且未被访问过（!vis[i][j]）的单元格时，说明发现了一个新的岛屿。

2. BFS 计算当前岛屿面积
   对每个新发现的陆地单元格，启动 BFS 计算整个岛屿的面积：

   • 将该单元格加入队列，标记为已访问（vis[i][j] = true），初始化面积计数器（count = 1）。
   • 从队列中取出单元格，检查其上下左右四个相邻单元格：
     • 若相邻单元格在网格范围内、值为 1 且未被访问过，则将其加入队列，标记为已访问，并将面积计数器加 1。
   • 队列处理完毕后，count 即为当前岛屿的面积。

3. 更新最大岛屿面积
   每次计算完一个岛屿的面积后，用当前面积更新全局最大面积（ret = max(ret, count)）。遍历结束后，ret 即为网格中最大岛屿的面积。

关键逻辑解析

• vis 数组的作用：记录已访问的陆地单元格，避免重复计算同一岛屿的面积。
• BFS 的优势：通过队列实现 “逐层扩散”，完整覆盖当前岛屿的所有陆地，确保面积计算准确。
• 面积统计：从起始单元格开始，每纳入一个新的陆地单元格，面积计数器就加 1，最终得到整个岛屿的面积。

总结

算法通过遍历网格发现新岛屿，利用 BFS 计算每个岛屿的面积，实时更新最大面积。核心是用 BFS 完整覆盖连通区域以计算面积和用访问标记避免重复统计，时间复杂度为 O(n*m)（n、m 为网格行列数），每个单元格最多被访问一次。

 

class Solution {typedef pair<int, int> PII;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int vis[50][50];int n, m;int ret = 0;public:int maxAreaOfIsland(vector<vector<int>>& grid) {n = grid.size(), m = grid[0].size();for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){if(grid[i][j] == 1 && !vis[i][j])dfs(grid, i, j);}}return ret;}void dfs(vector<vector<int>>& grid, int i, int j){queue<PII> q;q.push({i, j});vis[i][j] = true;int count = 1;while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x1 = a + dx[k], y1 = b + dy[k];if(x1 < n && x1 >= 0 && y1 < m && y1 >= 0 && grid[x1][y1] == 1 && !vis[x1][y1]){++count;q.push({x1, y1});vis[x1][y1] = true;}}}ret = max(ret, count);}
};

 

2.4 被围绕的区域

130. 被围绕的区域 - 力扣（LeetCode）

核心思想

1. 遍历网格，定位未访问的 'O'
   遍历整个网格，当遇到值为 'O' 且未被访问（!vis[i][j]）的单元格时，启动 BFS 处理该连通区域。

2. BFS 同步完成 “区域判断” 与 “单元格记录”
   在一次 BFS 中同时实现两个目标：

   • 记录区域所有单元格：用region数组存储当前连通区域的所有 'O' 的坐标。
   • 判断区域是否被包围：通过hasEdge标记该区域是否包含边缘单元格（位于网格边界：x=0、x=n-1、y=0、y=m-1）。
     • 若区域包含边缘单元格，hasEdge设为false（不被包围）。
     • 若区域无边缘单元格，hasEdge保持true（被完全包围）。

3. 根据判断结果处理区域
   BFS 结束后，若hasEdge为true（区域被包围），则遍历region数组，将所有记录的 'O' 转换为 'X'；否则不处理（保留边缘连通区域）。

关键逻辑解析

• 合并 BFS 的优势：避免两次遍历同一区域，一次 BFS 同时完成 “判断” 和 “记录”，减少冗余操作，时间复杂度优化为O(n*m)（n、m为网格行列数）。
• region数组的作用：临时存储当前区域的所有单元格，便于后续批量转换，无需二次遍历寻找目标单元格。
• hasEdge标记的作用：实时追踪区域是否接触网格边缘，决定该区域是否需要被转换为 'X'。

总结

算法通过一次 BFS 实现 “判断区域是否被包围” 和 “记录待处理单元格”，最终根据判断结果批量转换被包围区域。核心是用一次遍历同步完成多任务，既保证逻辑清晰，又提高了效率，完美解决 “被围绕的区域” 问题。

 

class Solution {typedef pair<int, int> PII;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int n, m;int vis[200][200];public:void solve(vector<vector<char>>& board) {n = board.size(), m = board[0].size();for(int i = 0; i < n; ++i){for(int j = 0; j  < m; ++j){if(board[i][j] == 'O' && !vis[i][j]){bfs(board, i, j);                  }}}}void bfs(vector<vector<char>>& board, int i, int j) // 判断有没有任何单元格位于 board 边缘{bool hasEdge = true;if(i == 0 || i == n - 1 || j == 0 || j == m - 1){hasEdge = false;}vector<PII> region;queue<PII> q;q.push({i, j});region.push_back({i, j});vis[i][j] = true;while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && board[x][y] == 'O' && !vis[x][y]){vis[x][y] = true;if(x == 0 || x == n - 1 || y == 0 || y == m - 1){hasEdge = false;}q.push({x, y});region.push_back({x, y});}}}if(hasEdge){for(auto [x1, y1] : region)board[x1][y1] = 'X';}}
};