PCA主成分分析
目录
什么是主成分分析?
KNN建模训练
数据标准化
数据PCA处理
保留主成分
降维后KNN
PCA(Principal components analysis),主成分分析,什么是主成分分析呢?介绍这个之前,先了解喜爱数据姜维(Dimensionality Reduction)。
任务:通过分析美国1929-1938年的经济数据,预测国民收入与支出
数据包括:雇主补贴、消费资料和生产资料,公共支出、利息等共计17项指标
什么是主成分分析?
通过17项指标,用主成分分析变成3项指标。
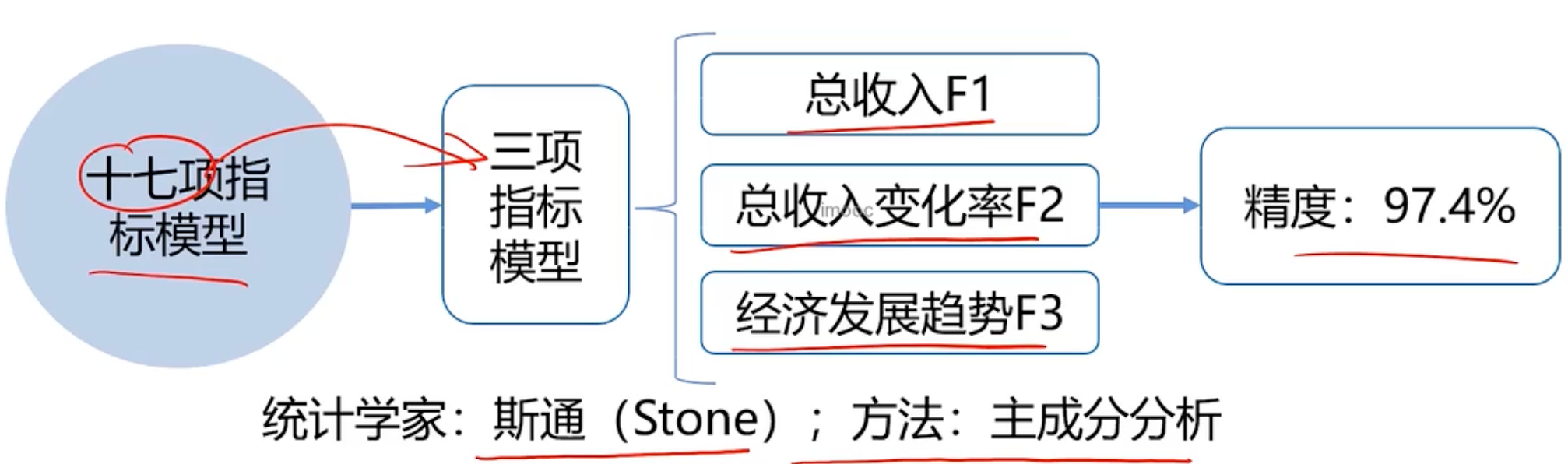
数据降维,在指定某些限定条件下,姜维随机变量个数,得到一组“不相关”的主变量的过程,如何理解呢不相关?比如刚才17个随机变量->3个不相关指标,相关性比如一个人的身高和体重有相关性。这样 就可以:
- 减少模型分析数据量,提升处理数据的效率,降低计算的难度
- 实现数据可视化
这里通过一个简单的例子来介绍数据降维。比如评估一个人的健康状况,这里仅通过两项指标来评估,身高和体重
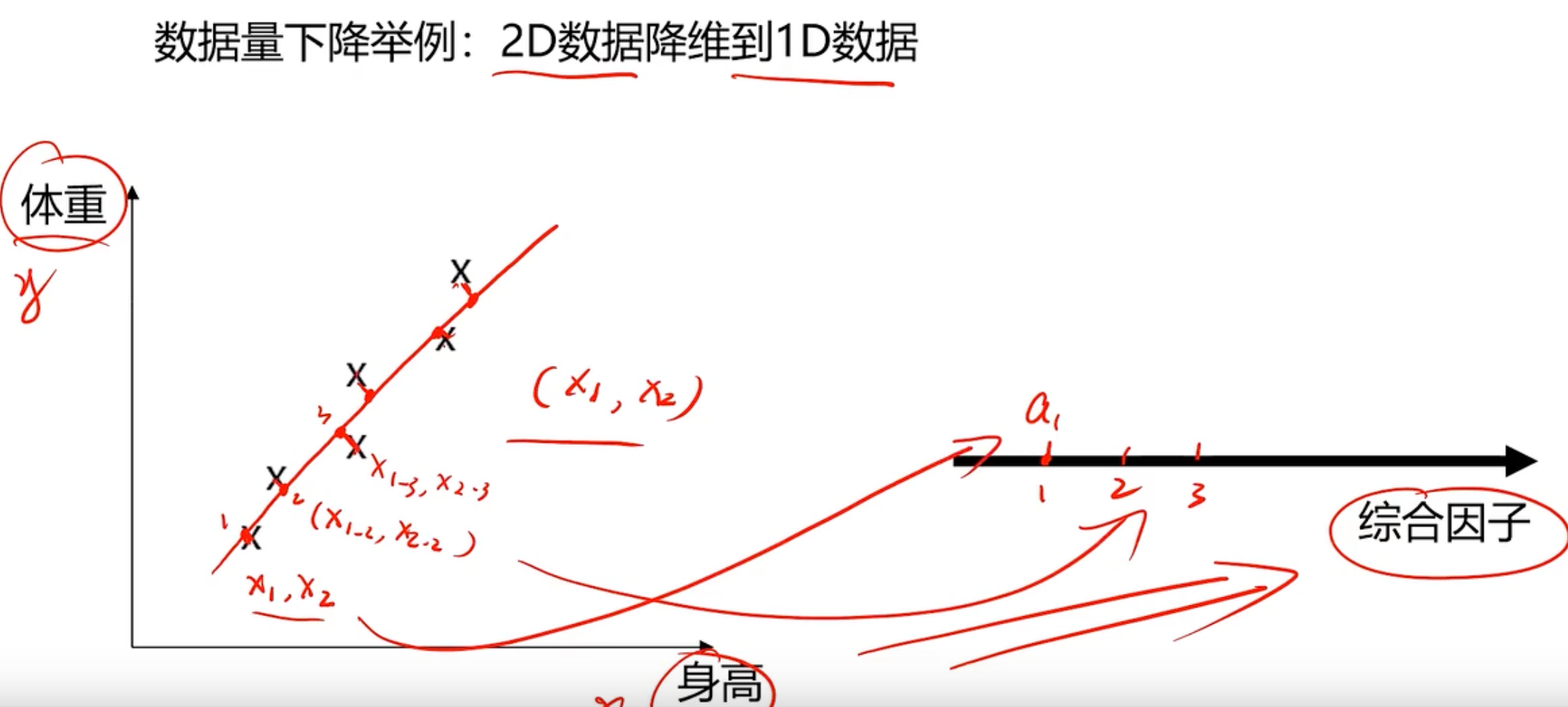
找到一条直线,把对应的点投影到这条直线上,那这个投影点就代表原来的数据,这样得到一个综合因子a对应健康的关系。同理3D到2维的
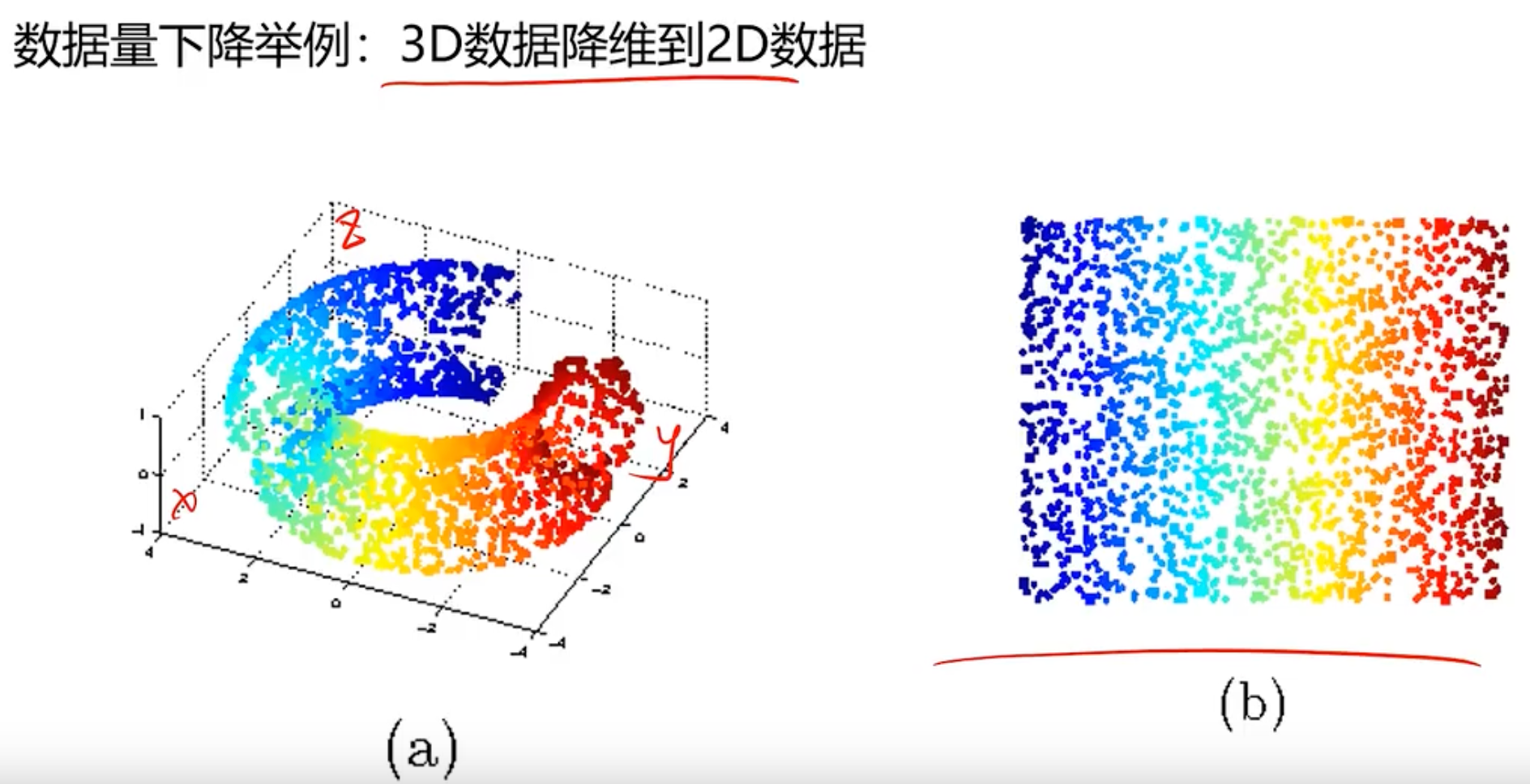
第三个示例是通过各个指标评估下国家的
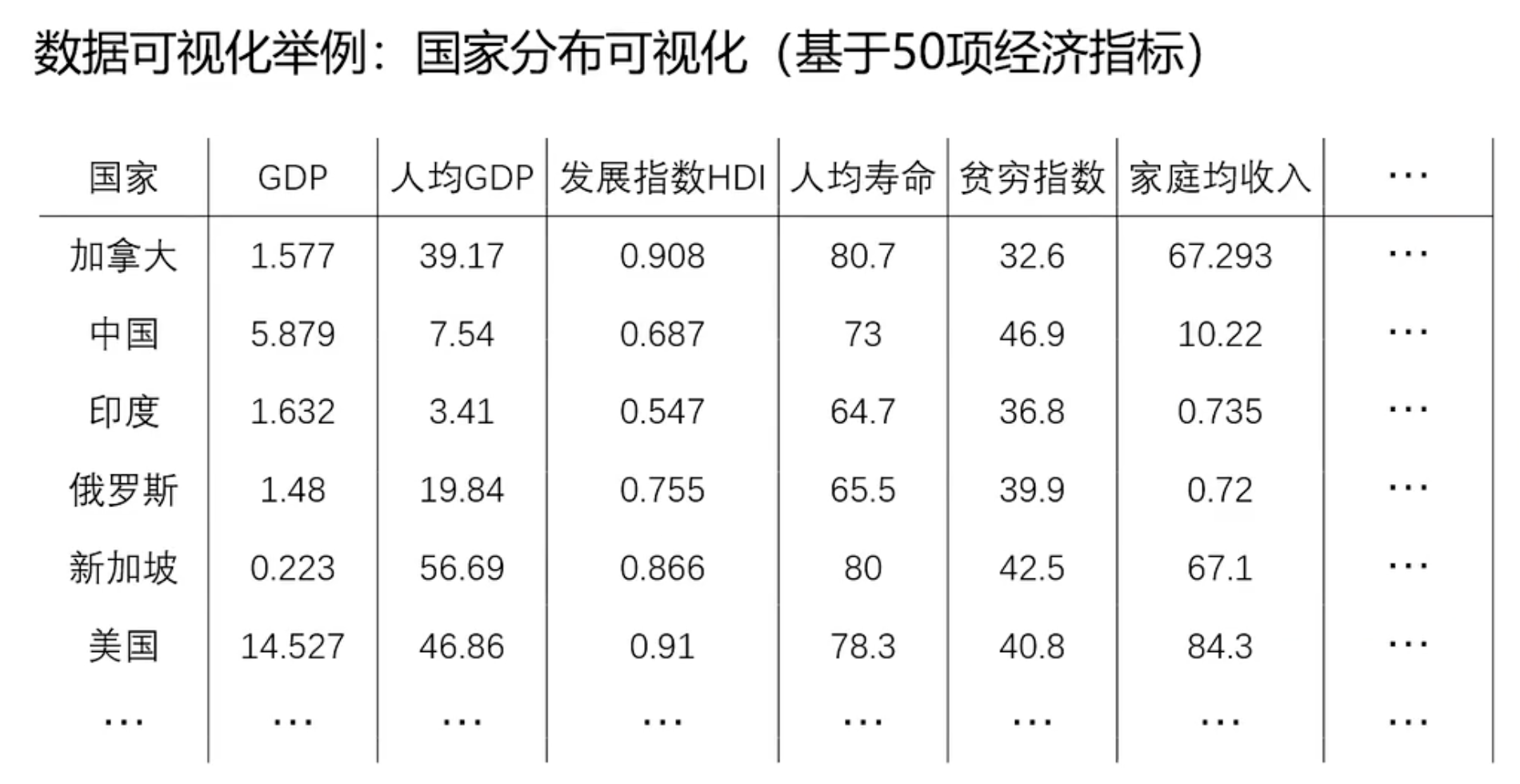
通过数据降维到2项指标
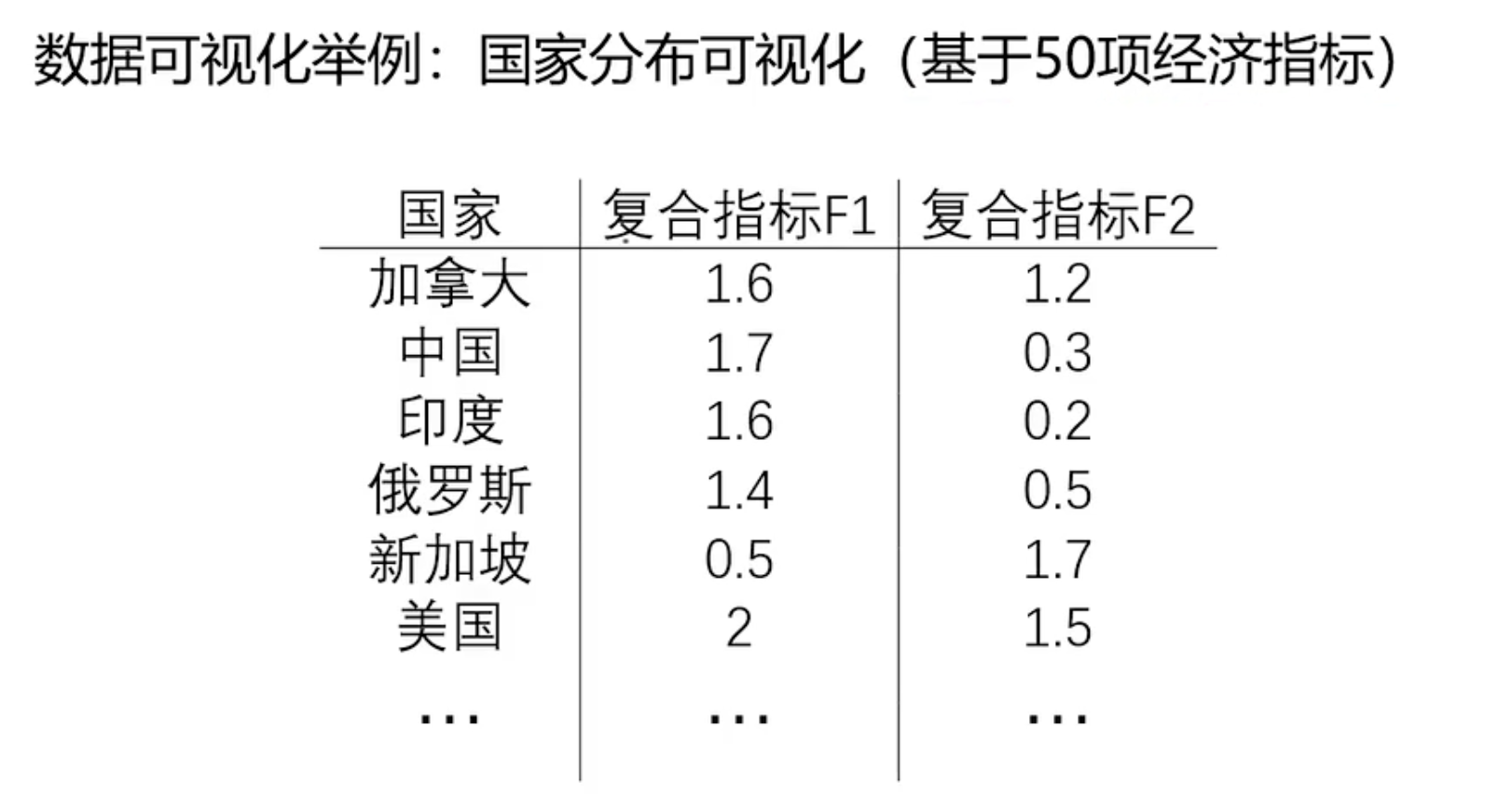
这样就可以进行可视化
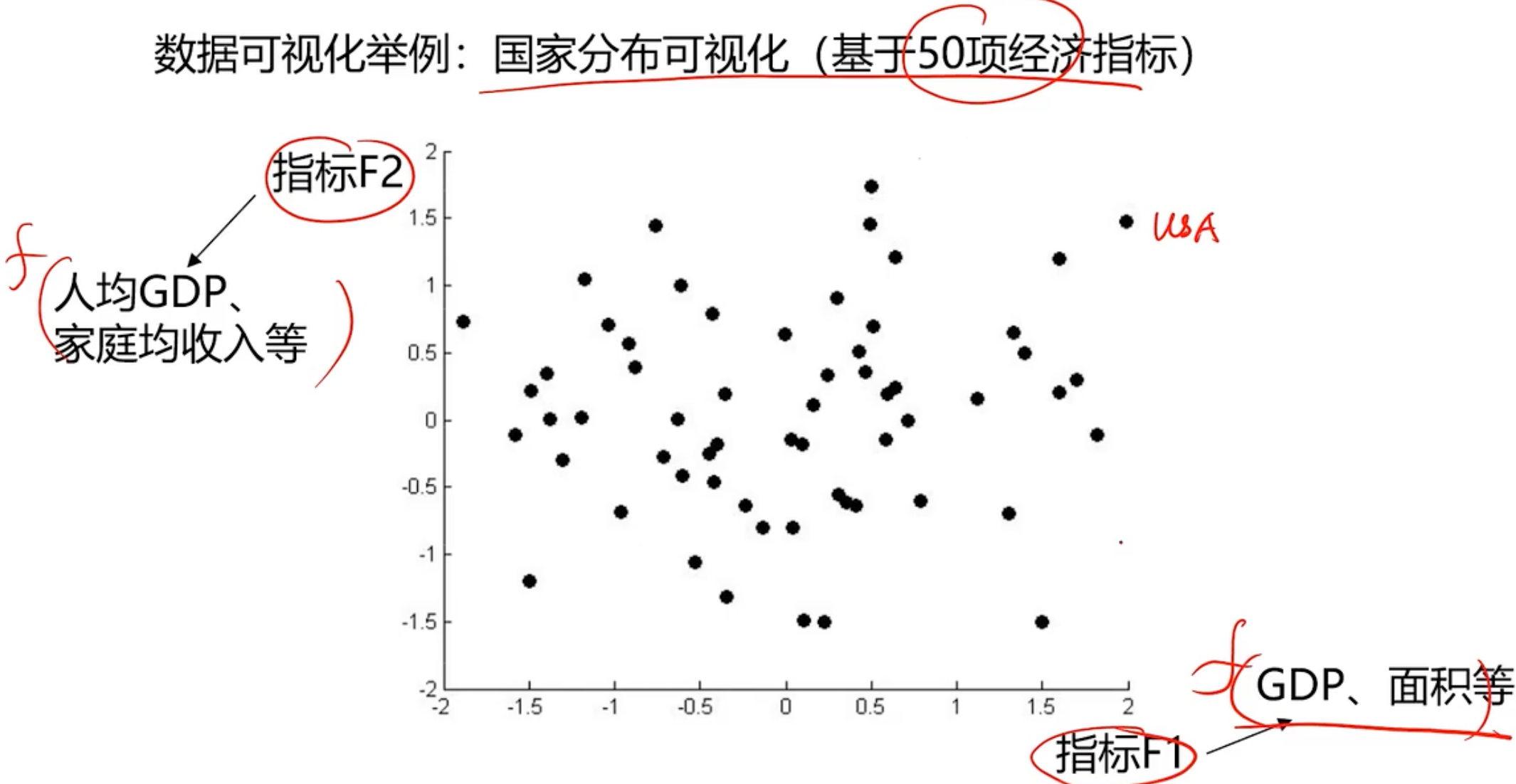
所以什么是PCA(Principal components analysis):数据降维技术中,应用最多的方法。目标是:寻找一个k(k<n)的新维度的数据,使得反映事物的主要特征。
核心就是在信息损失尽可能小的情况下,降低数据维度
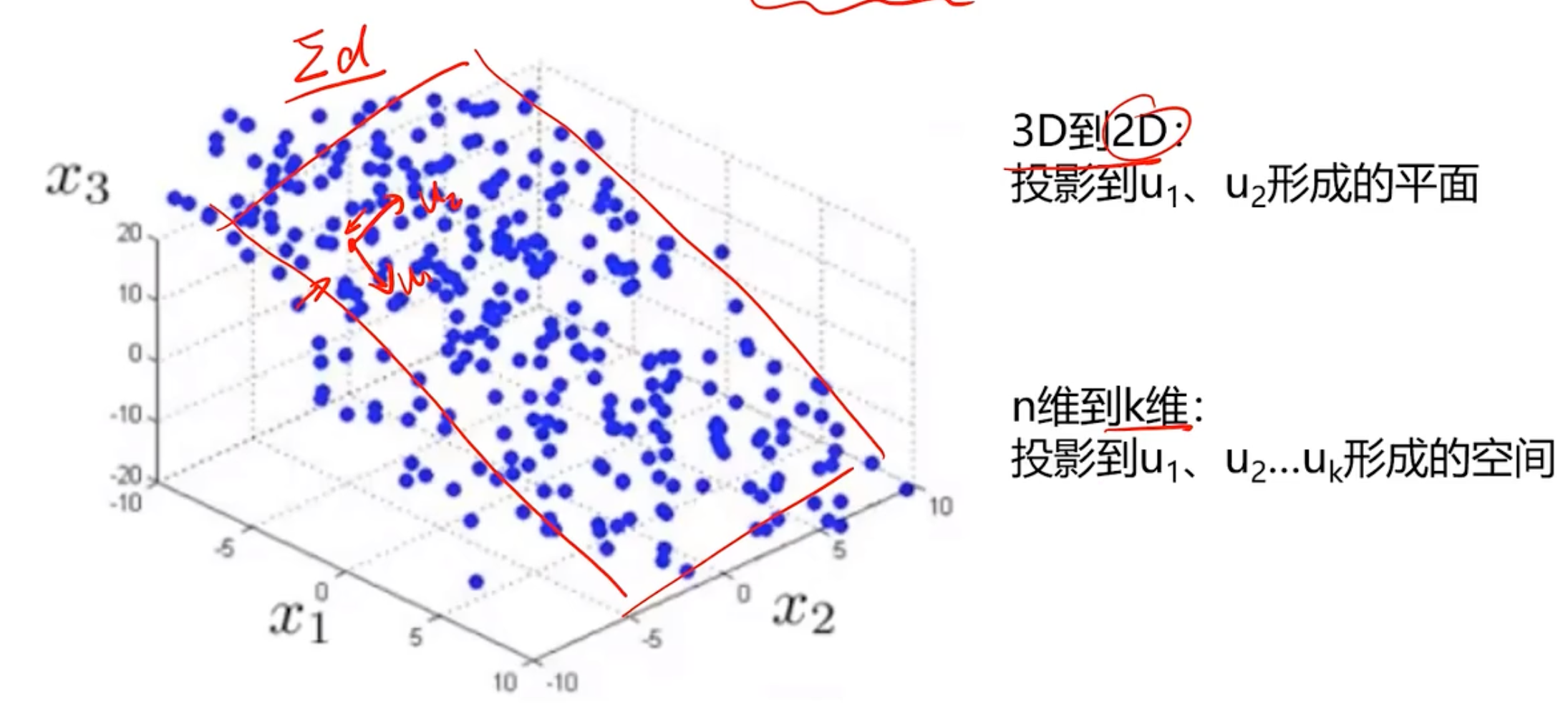
那如何能保留主要信息呢:投影后的不同特征数据尽可能分得开(即不相关)
具体如何实现呢?
使投影后数据的方差最大,因为方差越大数据越分散
计算过程如下:
- 原始数据预处理(标准化,
)
- 计算协方差矩阵的特征向量,数据在各个特征向量投影后的方差
- 根据需求(任务指定或者方差比例)确定降维维度k
- 选择k维特征向量,计算数据在其形成的空间投影
-
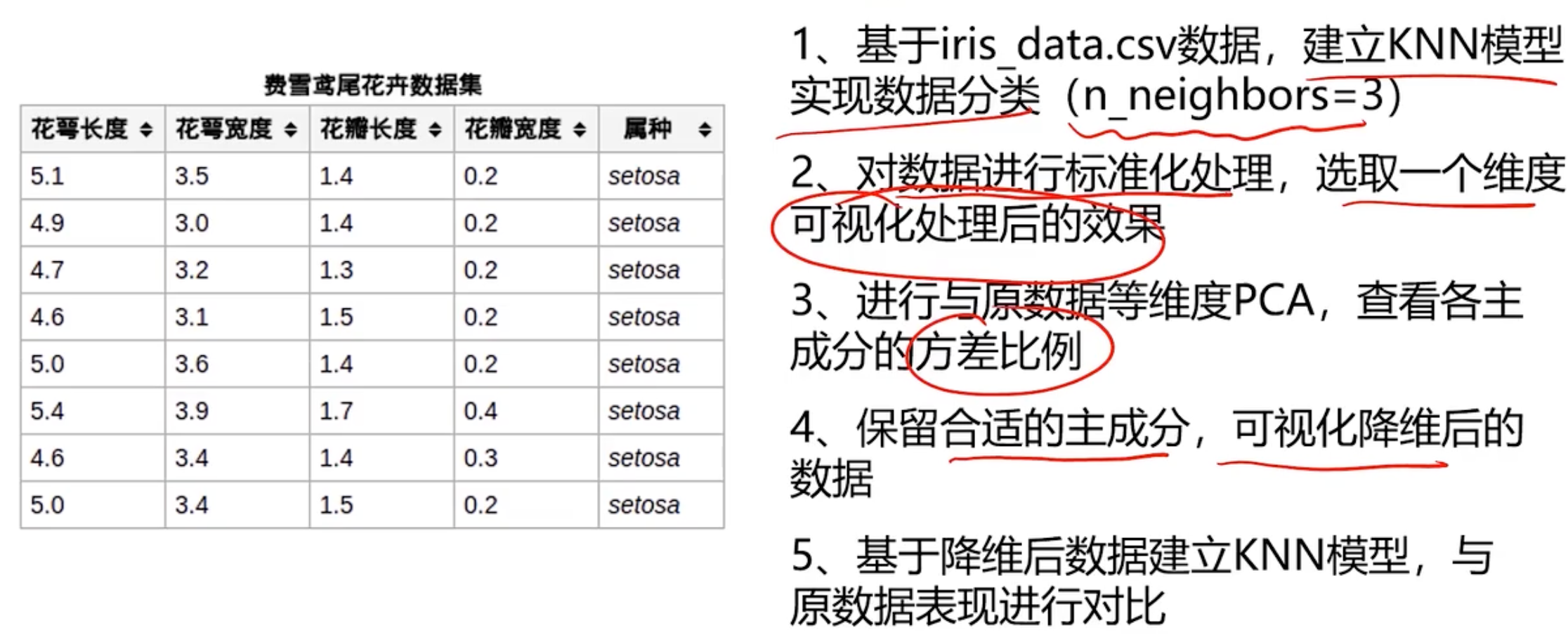
基于iris_data.csv数据,建立KNN模型实现数据分类(n_neighbors=3)
-
对数据进行标准化处理,选取一个维度可视化处理后的效果
-
进行与原数据等维度PCA,查看各主成分的方差比例
-
保留合适的主成分,可视化降维后的数据
-
基于降维后数据建立KNN模型,与原数据表现进行对比
KNN建模训练
import numpy as np
import pandas as pdfrom contants import PATHdata = pd.read_csv(PATH + 'iris_data.csv')
print(data.head())
定义X和y完成训练
# define X and y
X = data.drop(['target', 'label'], axis=1)
y = data.loc[:, 'label']
# print(y.head())# establish knn model and calculate the accuracy
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X, y)
y_predict = KNN.predict(X)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y, y_predict)
print(accuracy)准确率如下:
0.96数据标准化
# 数据标准化处理
from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
print(X_norm)这样发现不了原来的数据和现在的数据的差异,我们就把两个数据都可视化出来方便对比查阅
# calculate the mean and sigma
x1_mean = X.loc[:, 'sepal length'].mean()
x1_norm_mean = X_norm[:, 0].mean()
x1_sigma = X.loc[:, 'sepal length'].std()
x1_norm_sigma = X_norm[:, 0].std()
print(f"原始数据均值和标准差: ", x1_mean, x1_sigma)
print(f"数据标准化后的均值和标准差: ", x1_norm_mean, x1_norm_sigma)# 绘制原来的数据
from matplotlib import pyplot as pltfig1 = plt.figure(figsize=(12, 8))
plt.subplot(121)
plt.hist(X.loc[:, 'sepal length'], bins=100)
plt.subplot(122)
plt.hist(X_norm[:, 0], bins=100)
plt.show()
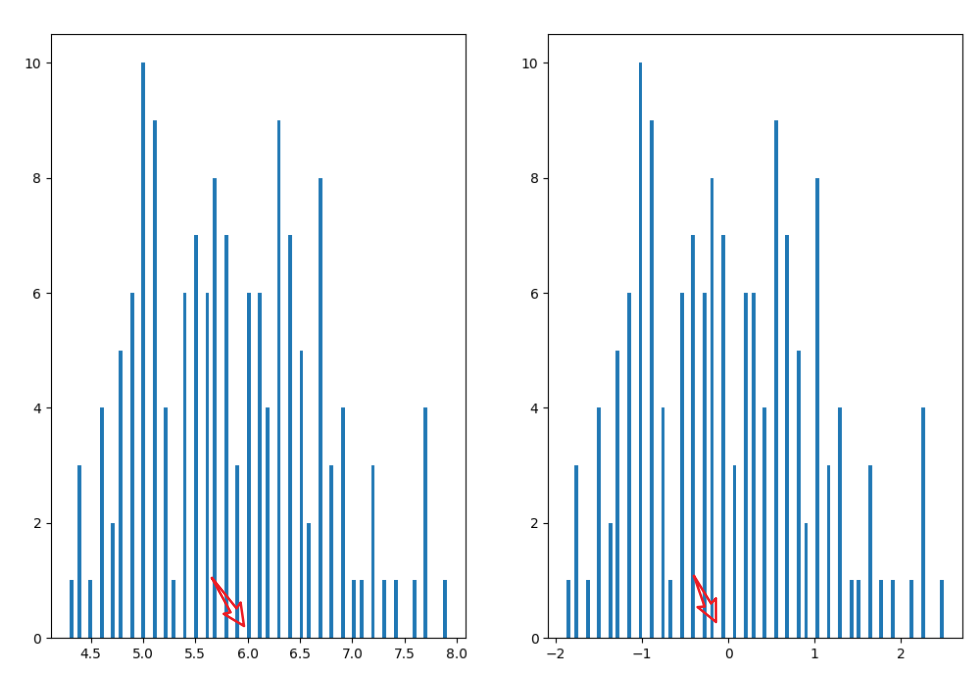
求解获取的均值和标准差如下:
原始数据均值和标准差: 5.843333333333334 0.828066127977863
数据标准化后的均值和标准差: -4.736951571734001e-16 1.0数据PCA处理
# pca analysis
print(X.shape)
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
X_pca = pca.fit_transform(X_norm)# calculate the variance ratio of each principle components 计算主成分方差是多少
var_ratio = pca.explained_variance_ratio_
print(var_ratio)输出如下所示:
[0.72770452 0.23030523 0.03683832 0.00515193]前两个主成分的方差比较大,后两个比较小,可以只用保留前两个
fig2 = plt.figure(figsize=(12, 8))
plt.bar([1,2,3,4], var_ratio)
plt.xticks([1,2,3,4], ['PC1', 'PC2', 'PC3', 'PC4'])
plt.ylabel('variance ratio of each PC')
plt.show()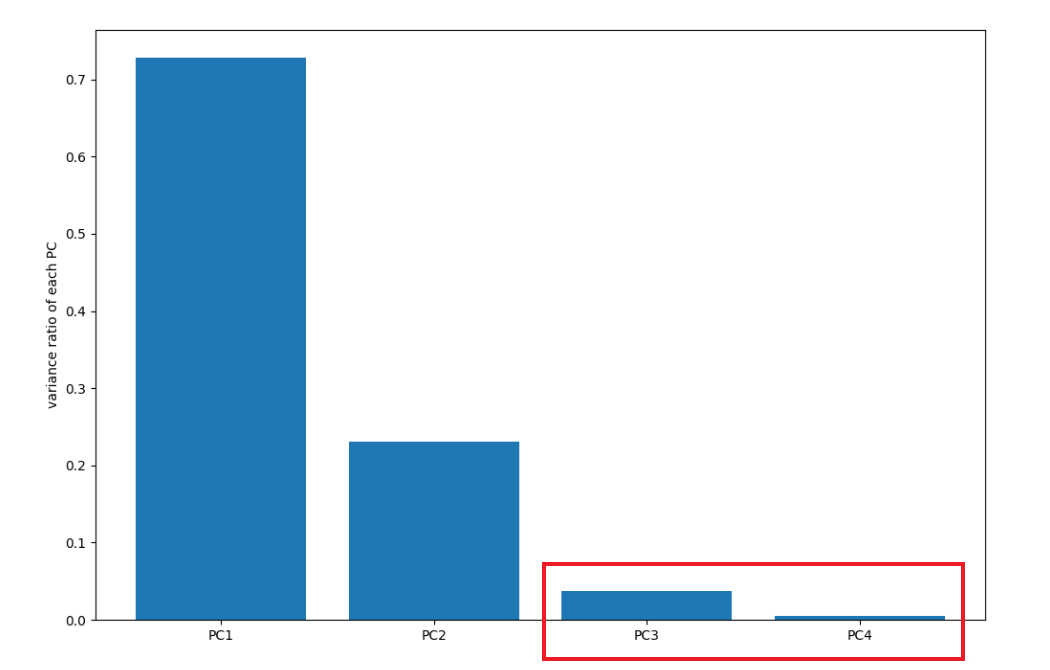
后面的数据的方差很小,说明数据的相关度比较高,存在重复的属性特征,所以只用保留前面两个,即确定了n_components=2.
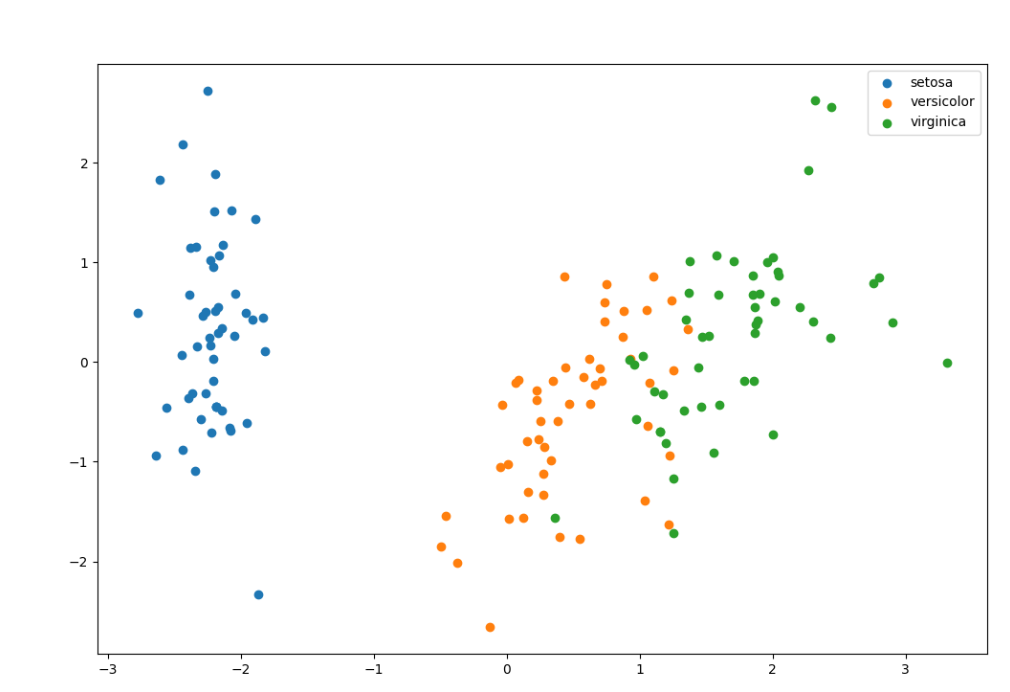
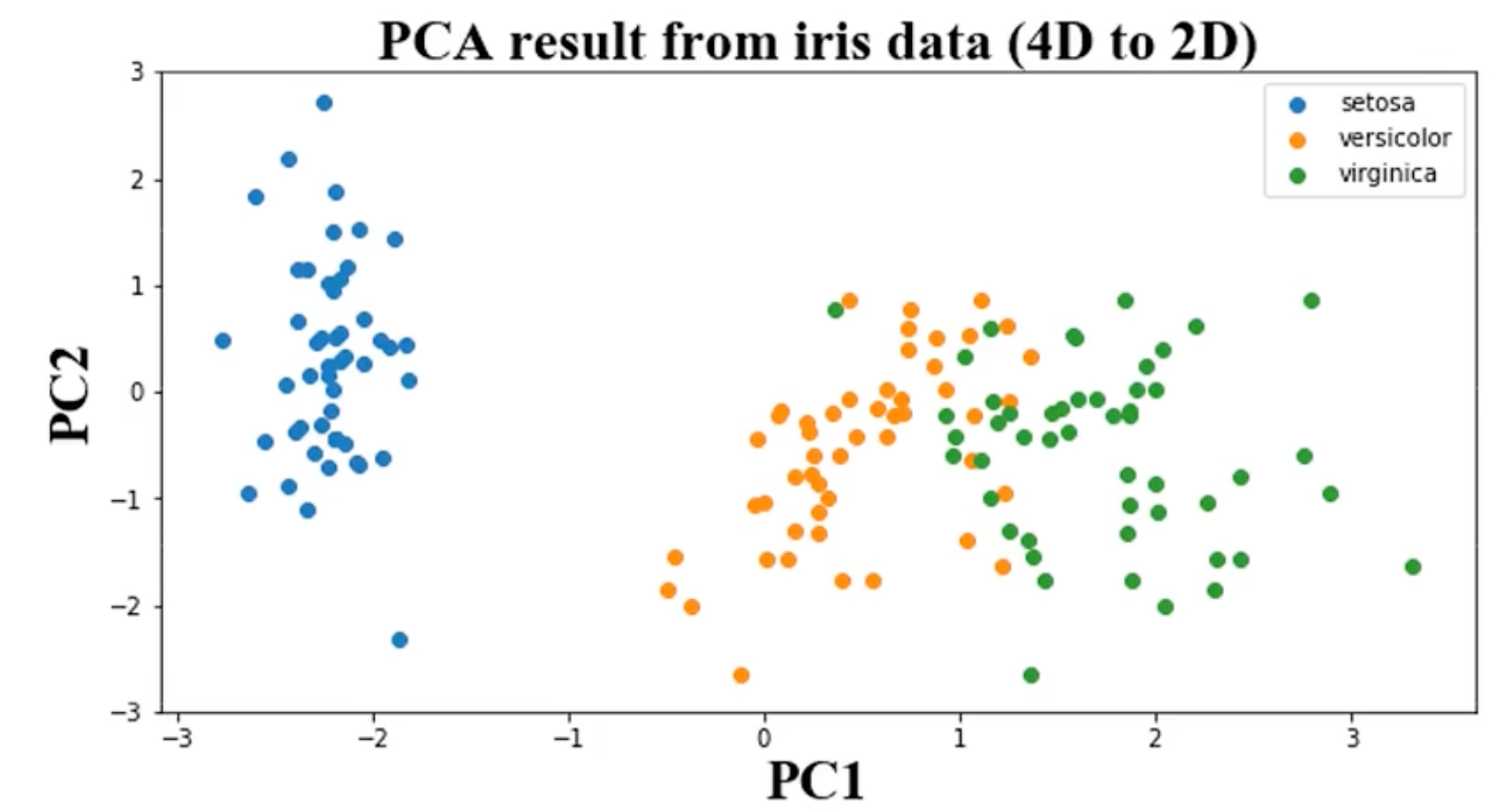
保留主成分
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_norm)
print(X_pca.shape)
fig3 = plt.figure(figsize=(12, 8))
setosa=plt.scatter(X_pca[:, 0][y==0], X_pca[:, 1][y==0])
ver=plt.scatter(X_pca[:, 0][y==1], X_pca[:, 1][y==1])
vir=plt.scatter(X_pca[:, 0][y==2], X_pca[:, 1][y==2])
plt.legend((setosa, ver, vir), ('setosa', 'versicolor', 'virginica'))
plt.show()降维后KNN
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(X_pca, y)
y_predict = KNN.predict(X_pca)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y, y_predict)
print(accuracy)输出为
0.9466666666666667准确率只下降了一点,说明效果还是不错的。但是维度降低了还是保留了数据的主要信息