马拉车(Manacher)算法
一、什么是马拉车(Manacher)算法
马拉车(Manacher)算法是一种高效求解字符串中最长回文子串的算法,由 Glenn Manacher 于 1975 年提出。它的核心优势是将时间复杂度优化到了线性 O (n)(n 为字符串长度),解决了传统方法(如中心扩展法)在处理回文时的效率问题。
二、为什么需要马拉车算法?
回文子串是指正反读完全一致的子串(如 “abcba”“abba”)。传统方法中,中心扩展法需要分别处理奇数长度和偶数长度的回文,且最坏时间复杂度为 O (n²);而马拉车算法通过统一奇偶数回文的处理方式和利用回文对称性减少重复计算,实现了线性效率。
三、如何实现?
1.预处理
首先对S做一个变换以简化问题。
在S的每个字符左右插入一个不属于S的字符,如'#'。
把
"abcba"变成了
"#a#b#c#b#a#"中心字符为'c'变换后中心字符为'#'。 经过这样的变换,字符串S的新长度都是奇数,中心字符都只有一个。 为了编程方便,在S的首尾再加上两个奇怪字符防止越界,如把"#a#b#b#a#"的首尾分别加上'$'和'&"变成"$#a#b#b#a#&"。经过变换后的字符串,不影响对其中回文串的认定
2.中心扩展法
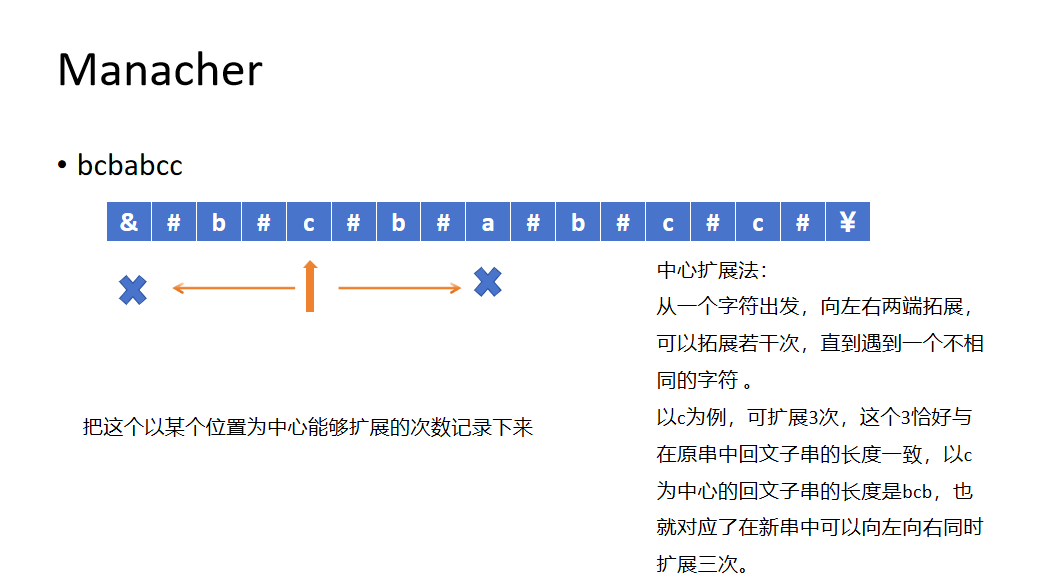
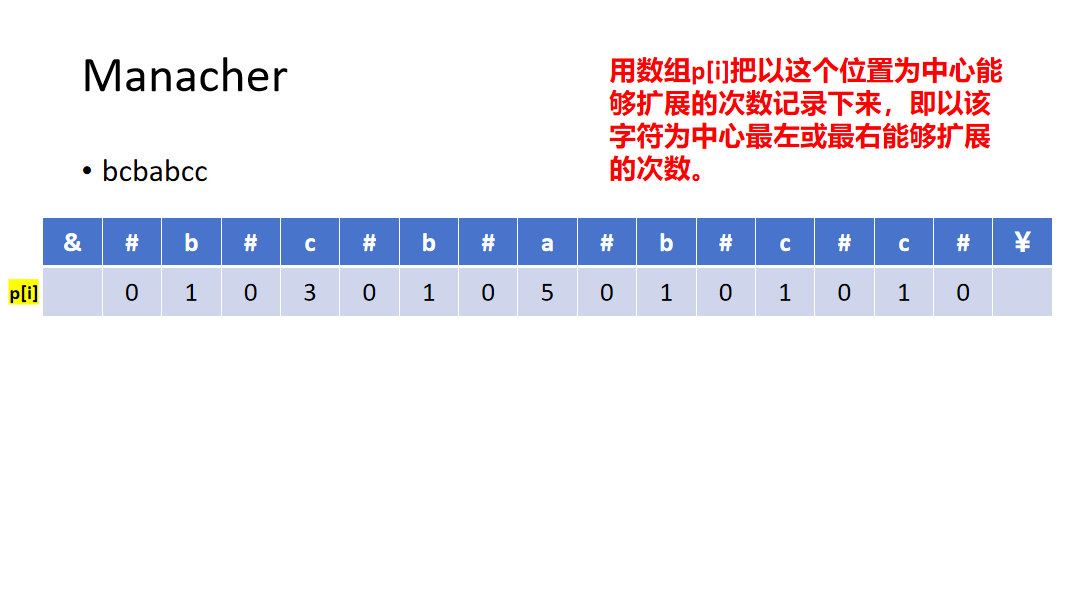
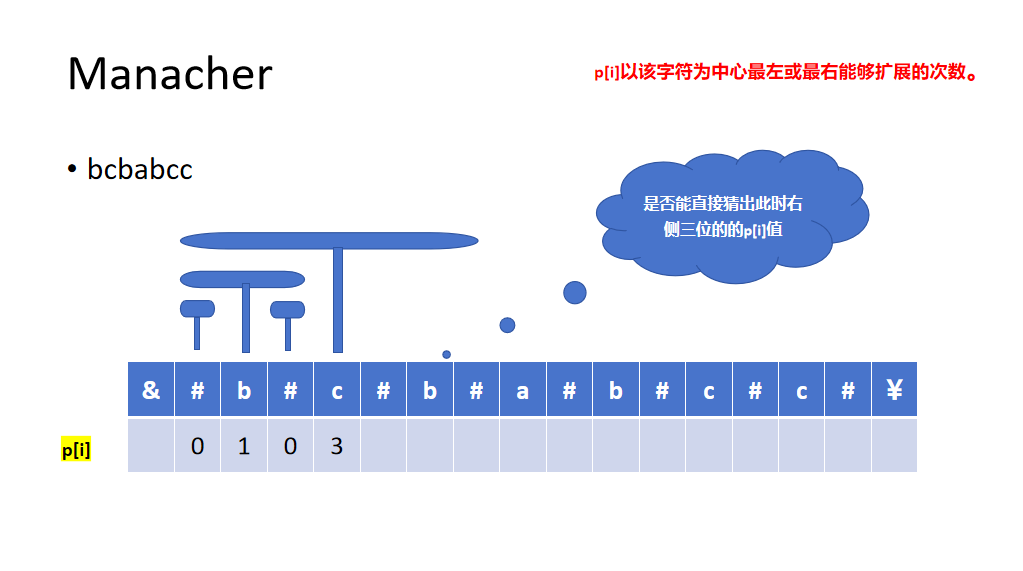
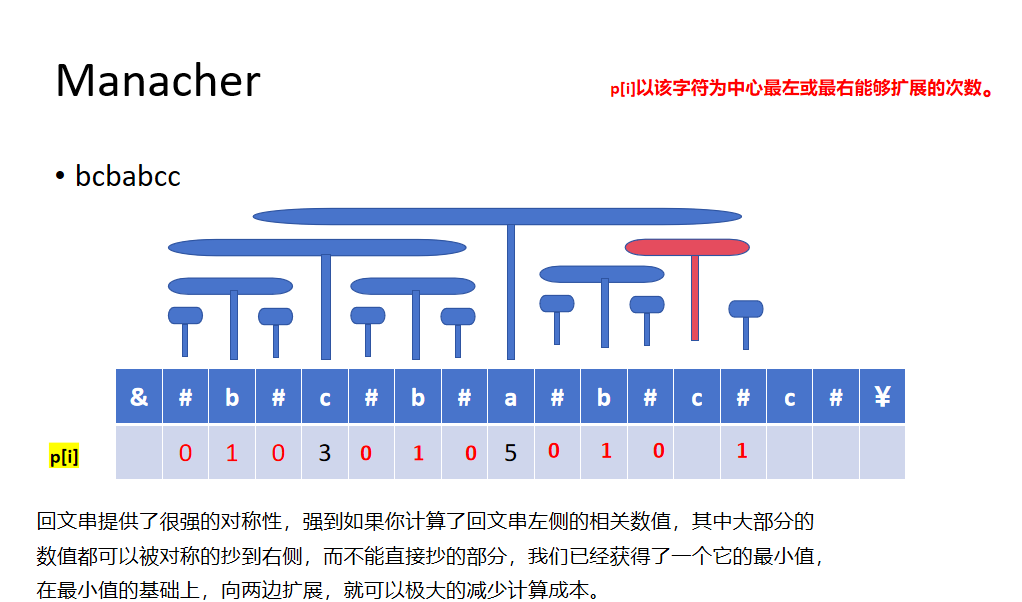
例题
https://www.luogu.com.cn/problem/P3805
#include<bits/stdc++.h>
using namespace std;
int n;int read(){int s=0,fl=1;char w=getchar();while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}return fl*s;
}
string s;
int main(){cin>>s;//输入字符串string T="^";for(char c:s){T+="#";T+=c;}//初始化添加标识符//R//含义:当前已知最右回文子串的右边界(R = C + P[C] - 1)。//作用:判断 i 是否在已知回文范围内,从而利用对称性优化计算。T+="#$";int n=T.size();vector<int> P(n,0);int C=0,R=0;for(int i=1;i<n-1;i++){int ii=2*C-i;//计算i关于回文中心的对称点if(R>i){//i 是在枚举预处理后字符串 T 的每个字符位置//i<R证明i位于已知回文的范围内,可以对称过去//P[ii] 表示对称点 ii 的回文半径。
//R - i 表示从 i 到已知回文右边界 R 的距离。
//结论:由于对称性,i 的回文半径至少为 P[ii],且不会超过 R - i(否则会超出已知回文范围)P[i]=min(R-i,P[ii]);}while(T[i+P[i]+1]==T[i-P[i]-1]){P[i]++;}//两边尝试扩展长度if(i+P[i]>R){C=i;R=i+P[i];}}//更新C和R的值int macn=0;for(int i=1;i<n-1;i++){macn=max(macn,P[i]);}cout<<macn;return 0;
}
