当前位置：首页 > news >正文

【RL第一篇】强化学习入门：核心概念全面详解

news 2025/7/20 7:50:53

一、强化学习

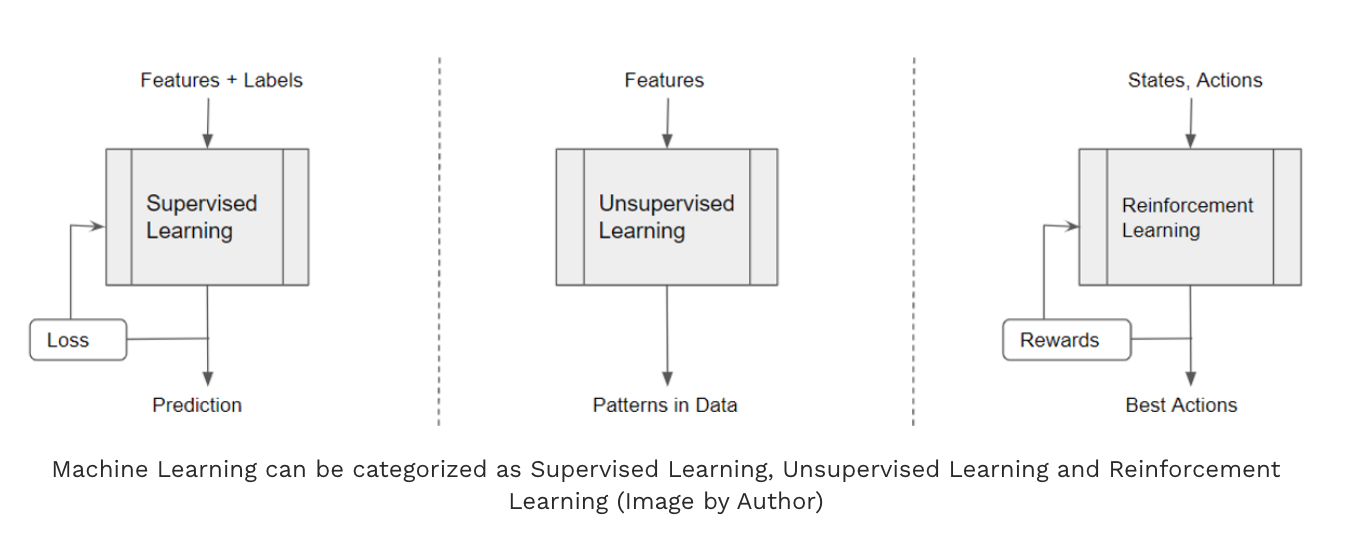
强化学习 (RL) 是机器学习的一个分支，专注于让Agent根据从环境中获得的奖励和惩罚进行学习和决策。

RL与监督学习和非监督学习不同，它不依赖于预先存在的标记数据集。相反，会与环境交互，以奖励或惩罚的形式接收反馈，并学习相应地优化其行为。

二、概念列表

代理（Agent）
环境（Environment）
状态（state）
动作（action）
策略（policy）
轨迹（trajectory）
奖励（reward）和回报（Return）
状态价值函数（Value function）和动作价值函数（Q-function）

三、通用概念

3.1 代理（Agent）

这里的Agent指代的并非目前火热的function call的Agent，更像是一种代称。

代理可以是一种系统或程序，它与环境交互，以学习如何实现特定目标。通过接收来自环境的反馈（以奖励或惩罚的形式）进行学习。代理的最终目标是学习一种策略（policy），即从环境状态（state）到动作（action）的映射，从而最大化其长期预期奖励（Value）。

包含三个主要组件：

策略
价值函数
学习算法

策略是代理根据当前环境状态选择动作的策略。价值函数估算代理从特定状态和动作中获得的预期长期奖励。学习算法根据从环境收到的反馈更新代理的策略和价值函数。

3.2 环境（Environment）

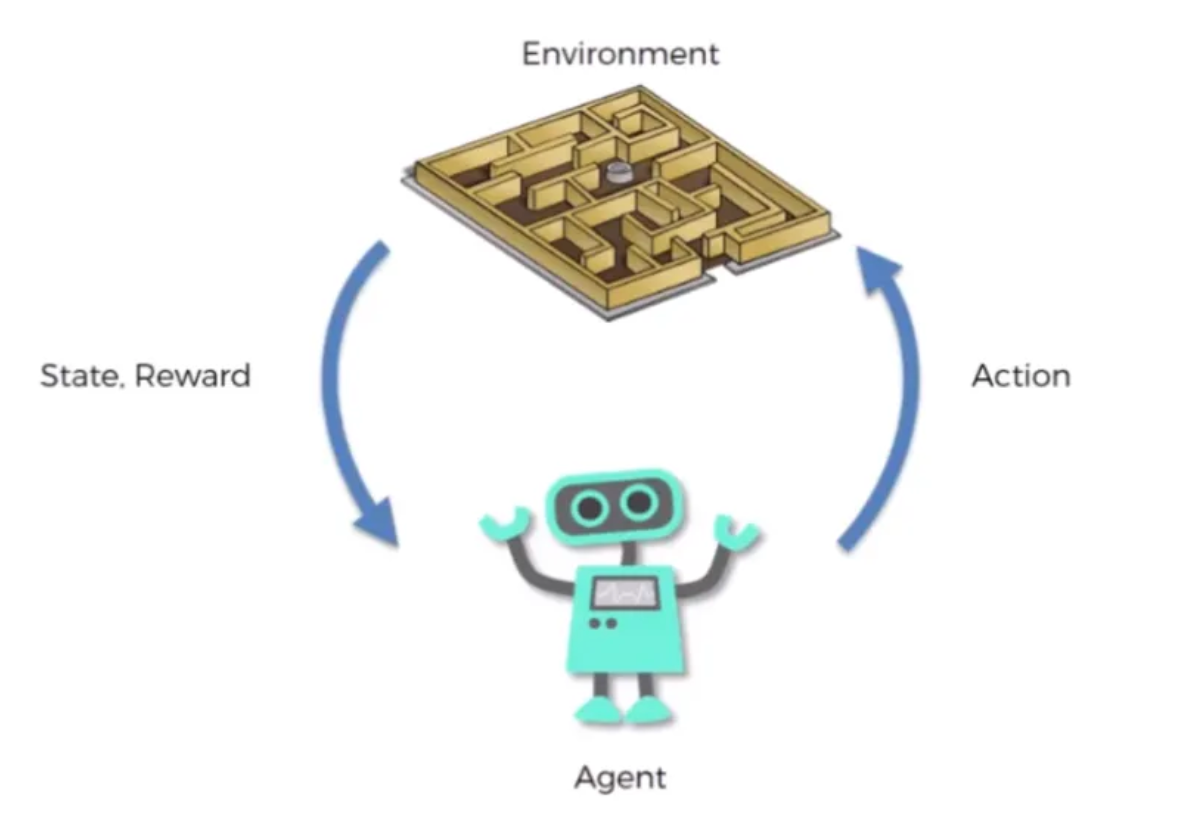
在强化学习中，“环境”指的是代理运行的外部世界或系统。它是代理与之交互并接收反馈的环境，代理的目标是从这些交互中学习并优化其行为以实现特定目标。

强化学习中的环境可以是任何行事，从虚拟模拟到物理系统。环境为代理提供描述系统的当前状态。代理会利用这些观察值来决定它应该采取的行动，以及它采取哪些行动来改变环境状态。

环境还会根据代理采取的操作，以奖励或惩罚的形式向其提供反馈。这些奖励会向代理发出信号，使其强化或抑制某些行为，而代理的目标是随着时间的推移最大化其累积奖励。

四、关键概念

接下来就以乒乓球这个运动的游戏来举例：

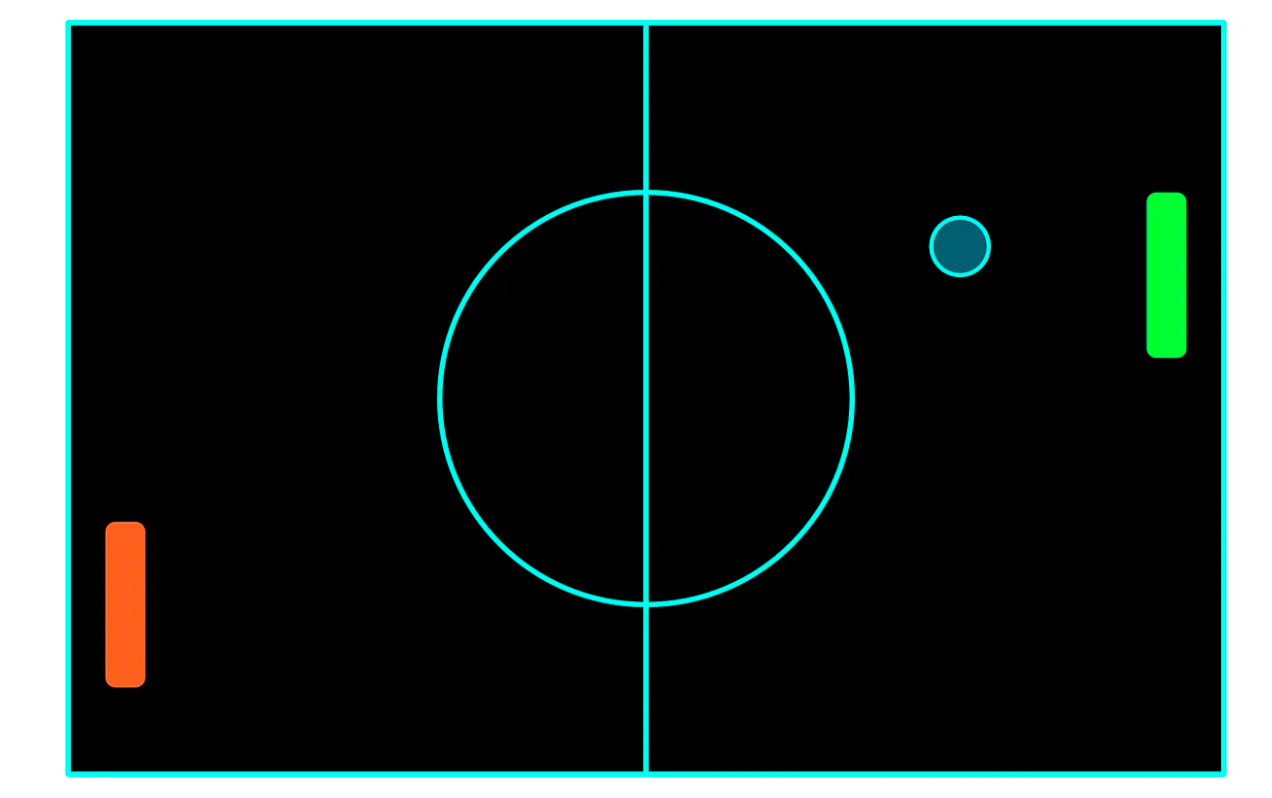
乒乓球的规则大家一定很熟悉，目前有两个玩家，红色和绿色，将操作绿色球拍的玩家视为代理。乒乓球的目标是将球弹回，使其越过其他玩家的球拍。当任何一名玩家成功将球弹过对方玩家时，即可得分，球将再次从场地中心移动。得分最高的玩家获胜

4.1 状态（state）

状态是指代理所处环境的当前情况。包含代理做出决策和采取行动以最大化其回报所需的所有相关信息，通常是一个向量、矩阵或其他张量。

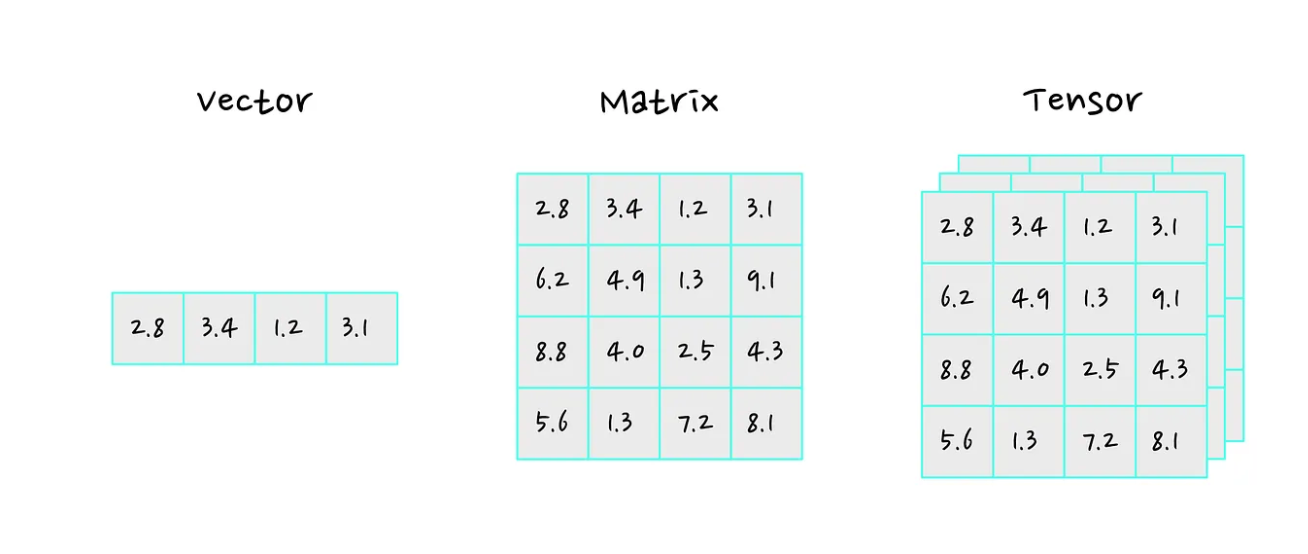
状态和时间是相关的，时间步 t 的状态表示为
$ {s}_{t} $

以乒乓球为例，表示乒乓球局的当前状态，可以是一个向量/矩阵来表示，包含球拍的位置、球的位置以及球的角速度，根据这些信息代理就可以做出行动了。

还有另外一个思路，就是通过视觉的方式来提供当前的状态。因为我们要表示球的角速度，所以需要多个帧来表示：

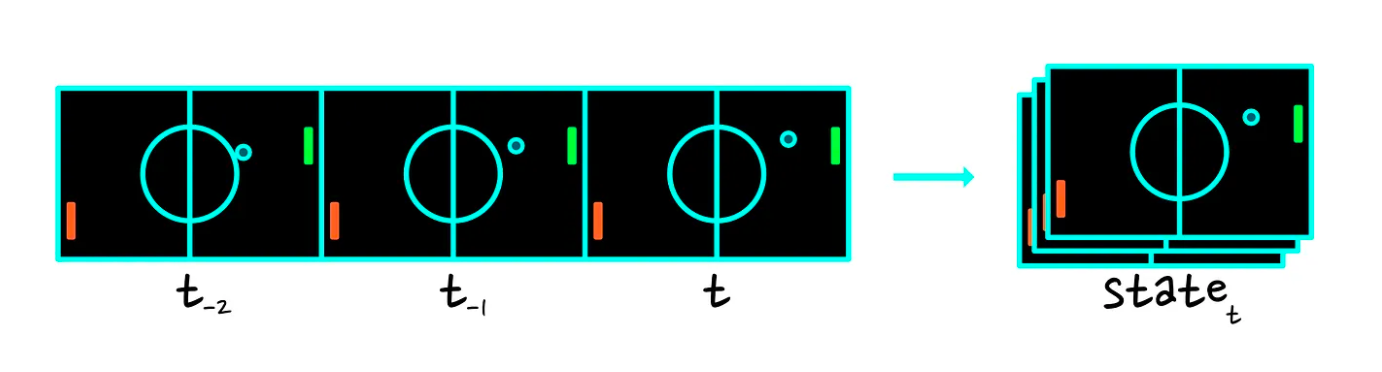
4.2 动作（action）

动作是指代理根据环境状态做出的决策。

行动也包含离散行动和连续的行动。

在乒乓球中希望代理可以上下移动

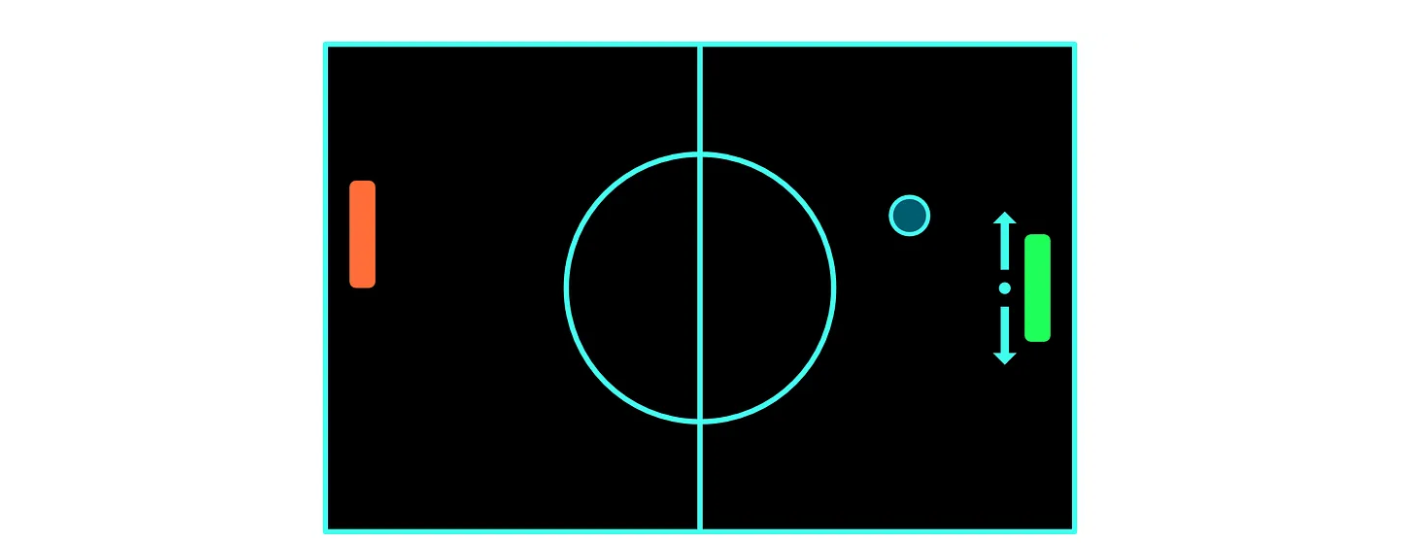
4.2.1 离散行动（discrete action）

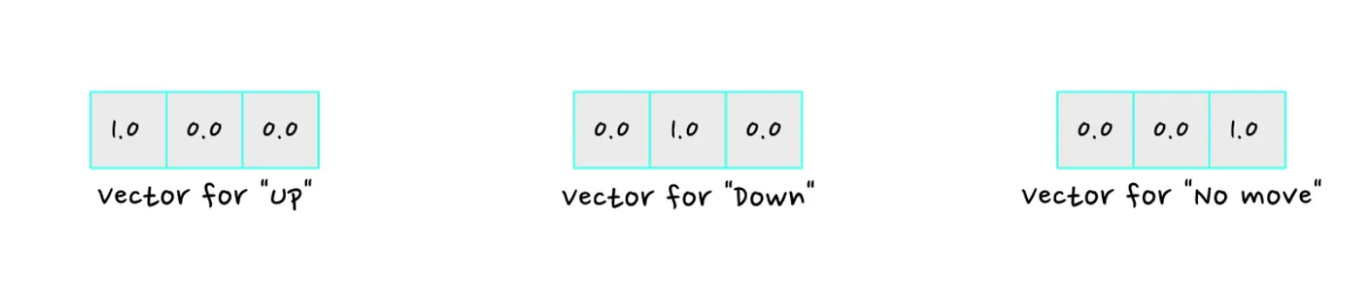
将动作定义为“向上”、“向下”和“不动”，其中向上，向下动作的大小是我们预定好的，是个枚举值。为了更好的表示三个action，可以采用one hot的多维度向量

4.2.2 连续行动（continuous action）

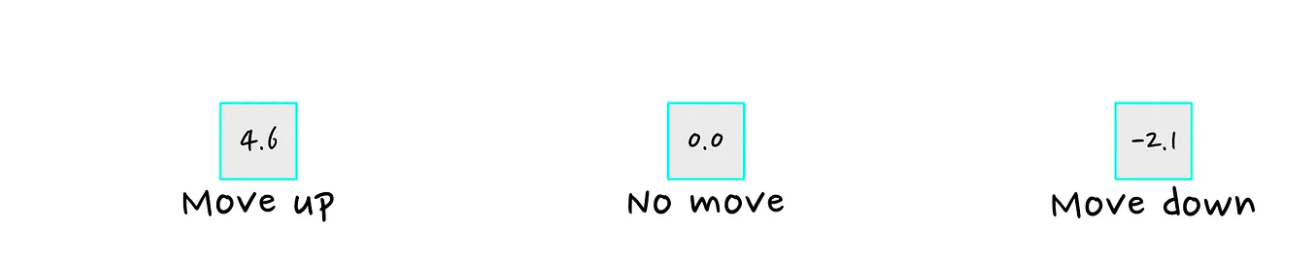
自然也可以是连续值的形式，比如上下多少个像素点，粒度可以根据自己的需求设定。这种情况下可能一个标量就足够了。

4.3 策略（policy）

策略是从状态到动作的映射。决定了Agent从特定状态开始的行为方式。

主要分为两种类型：确定性策略和随机性策略

4.3.1 确定性策略（Deterministic policy）

确定性策略以概率 1 输出一个动作，所以是确定的，对于st就会映射出at

$at=μθ(st)a_t=\mu_\theta(s_t)$

其中t为时间步， st为为t时刻的状态，通过 $μθ\mu_\theta$ 可以映射到at，其中u的参数为 $θ\theta$ ，在大模型任务里u就对应于llm， $θ\theta$ 为llm的parameters，我们的目的就是优化参数来达到目标。

4.3.2 随机性策略（Stochastic policy）

随机性策略对于一个st有一定的概率映射at：

$at∼πθ(⋅∣st)a_t \sim \pi_\theta(\cdot \mid s_t)$

通常用 $πθ\pi_\theta$ 来代表随机概率映射

4.4 轨迹（trajectory）

轨迹指代一系列状态和动作，一个时间的序列：

$)\tau = \left(s_0, a_0, s_1, a_1, \dots\right)$

4.5 奖励（reward）

奖励是代理在执行操作后从环境接收到的标量反馈信号。奖励的目的是表明代理在实现其目标方面的表现，通常目标是最大化随时间推移的累积奖励量。

奖励可以是正数、负数或零。特定时间步 t 的奖励为：

$r_t = R(s_t, a_t, s_{t+1})$

其中R为奖励函数（Reward function）， $r_t$ 由t时间状态 $s_t$ +t时间采取的行动 $a_t$ +新状态 $s_{t+1}$ 共同决定。

4.6 回报（Return）

回报为所有时间步的奖励总和，分为：有限时域未折现回报（Finite-horizon undiscounted return）和无限时域折现回报（Infinite-horizon discounted return），Agent的目标是学习一种策略Policy，以最大化未来奖励的预期总和，即预期回报。

4.6.1 Finite-horizon

$R(τ)=∑t=0TrtR(\tau) = \sum_{t=0}^{T} r_t$

从当前状态到目标状态的奖励总和（即轨迹的总reward），具有固定的时间步长或有限个时间步长 Τ

4.6.2 Infinite-horizon

$R(τ)=∑t=0∞γtrtR(\tau) = \sum_{t=0}^{\infty} \gamma^t r_t$

时间步为♾️，且引入折扣因子决定需要考虑多大程度的未来奖励，折旧因子介于 0 到 1 之间。在极端情况下，γ = 0 表示智能体只关心当前奖励，而 γ = 1 表示所有未来奖励都被考虑在内。折现因子越低，未来回报的价值就越低（考虑的越少）。

举个例子理解折旧因子存在的必要性：人们通常认为越早获得奖励越好。例如，现在获得现金比以后更好，因为由于通货膨胀，现金以后可能会贬值。

五、价值函数

价值函数是估算状态或状态-动作对的价值的函数。它表示特定状态或动作在实现目标方面的效果。

强化学习中的价值函数有两种：状态价值函数和动作价值函数。

5.1 状态价值函数（Value function）

在给定状态下期望获得多少奖励，即从给定状态 s 开始并遵循当前策略可以获得的预期累积奖励

$Vπ(s)=Eτ∼π[R(τ)∣s0=s]V^\pi(s) = \underset{\tau \sim \pi}{\mathrm{E}}\left[ R(\tau) \mid s_0 = s \right]$

这里使用的是不确定性的策略 $π\pi$

5.2 动作价值函数（Q-function&Q函数）

定义为代理从状态 s 开始，采取动作 a，并遵循当前策略可以获得的预期累积奖励。它将状态-动作对作为输入，并输出在该状态下采取该动作并随后遵循给定策略的预期长期奖励。

通过学习 Q 函数，代理可以选择最大化预期长期奖励的动作，而这正是许多强化学习任务的目标

$Qπ(s,a)=Eτ∼π[R(τ)∣s0=s,a0=a]Q^\pi(s, a) = \underset{\tau \sim \pi}{\mathrm{E}}\left[ R(\tau) \mid s_0 = s, a_0 = a \right]$

在策略 π 下，处于状态 s 并采取行动 a 的价值，简而言之，处于某个状态并采取某个行动的预期收益有多大。

5.3 Value function和Q函数的关系

最佳状态价值函数为：

$V∗(s)=max⁡πVπ(s)∀s∈SV^*(s) = \max_\pi V^\pi(s) \quad \forall s \in \mathbb{S}$

如果知道最佳状态价值函数，它对应的策略就是最优策略为：

$π∗=arg⁡max⁡πVπ(s)∀s∈S\pi^* = \arg\max_\pi V^\pi(s) \quad \forall s \in \mathbb{S}$

因为 V*(s) 是从状态 s 开始的最大预期总回报，因此它将是 Q*(s, a) 所有可能动作中的最大值。

当策略为确定性策略的时候，V和Q有这样的等式：

$V∗(s)=max⁡aQ∗(s,a)V^*(s) = \max_a Q^*(s, a) \quad$

当策略为不确定性策略的时候，则为：

$Vπ(s)=Ea∼π(a∣s)Qπ(s,a)V_\pi(s) = \mathbb{E}_{a \sim \pi(a|s)} Q_\pi(s, a)$

对于每个action的reward如何计算，那就是advantage函数等式：

$Aπ(s,a)=Qπ(s,a)−Vπ(s)A_\pi(s, a) = Q_\pi(s, a) - V_\pi(s)$

六、强化学习综述

https://arxiv.org/abs/2412.05265

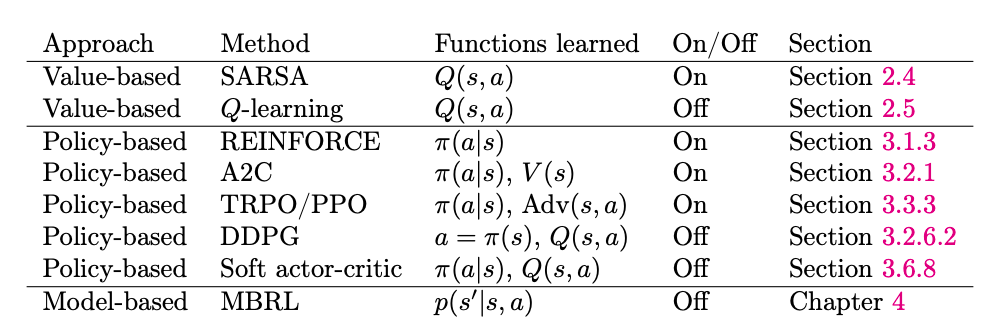
前期的方法如Q-learning和REINFORCE分别代表着两个主流的强化学习方向

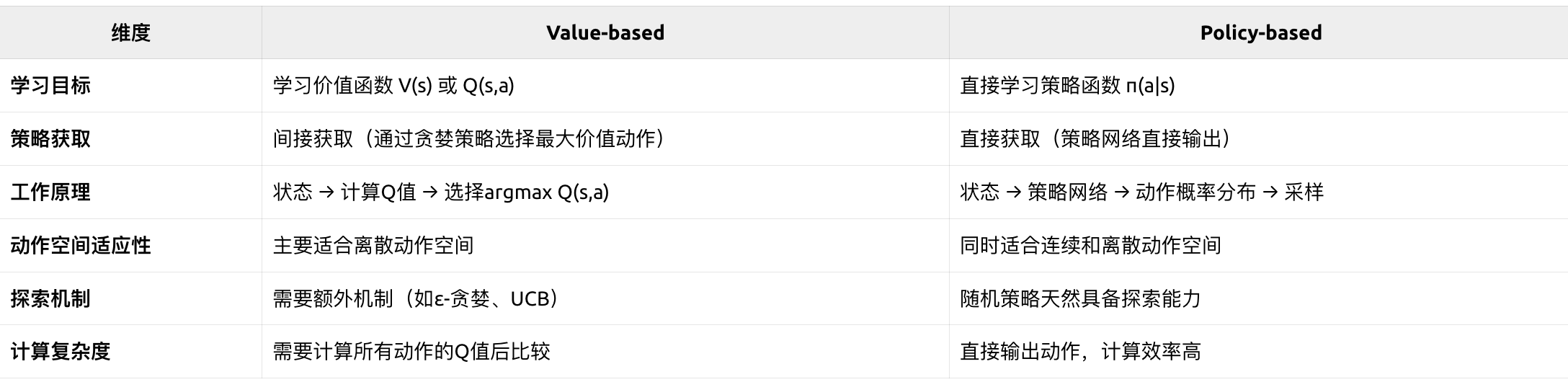
Value-based：通过学习状态 $Vπ(s)V^\pi(s)$ 或状态-动作对的价值函数 $Qπ(s,a)Q^\pi(s, a)$ 来指导决策，如：Q-Learning、DQN
Policy-based：直接学习和优化策略函数 $πθ\pi_\theta$ ，如：REINFORCE

Ref

https://medium.com/@cedric.vandelaer/reinforcement-learning-an-introduction-part-2-4-46a1491a2451
https://towardsdatascience.com/reinforcement-learning-made-simple-part-1-intro-to-basic-concepts-and-terminology-1d2a87aa060/
https://arjun-sarkar786.medium.com/reinforcement-learning-for-beginners-introduction-concepts-algorithms-and-applications-3f805cbd7f92

查看全文

http://www.dtcms.com/a/287769.html