Python趣味算法：抓交通肇事犯（车牌号谜题解析）

🔍 一道经典的数学谜题，如何用Python高效求解？本文带你揭秘算法优化全过程！

 看在每天坚持分享的份上，点个关注吧(づ￣ 3￣)づ

关注是我更新的动力￣︶￣∗￣︶￣∗)

作者会分享更多涉及到各种编程语言的有趣知识！（＾∀＾●）ﾉｼ 

目录

问题描述：肇事车牌的数学特征

一辆卡车肇事逃逸，三位目击者提供以下线索：

数学建模：求4位数 $a_1a_2a_3a_4$ 满足：

算法设计思路

基础解法：三重循环暴力破解

算法流程图（Mermaid） 

性能优化：减少无效循环

数学优化：平方根验证法

性能对比分析

完整代码实现 

运行结果验证

数学验证：

算法拓展思考

总结与讨论

版权声明：本文代码原创部分由CSDN博主「坐路边等朋友」提供，技术解析部分原创，转载请注明出处。  

---

问题描述：肇事车牌的数学特征

一辆卡车肇事逃逸，三位目击者提供以下线索：

• 甲：牌照前两位数字相同

• 乙：牌照后两位数字相同，但与前两位不同

• 丙（数学家）：4位车号是一个整数的平方

数学建模：求4位数 $a_1a_2a_3a_4$ 满足：

1.  a₁ = a₂ (1≤a₁≤9, 0≤a₂≤9)

2. a₃ = a₄ (0≤a₃,a₄≤9)

3. a₁ ≠ a₃

4. 1000a₁ + 100a₂ + 10a₃ + a₄ = x² (x∈ℤ)

算法设计思路

基础解法：三重循环暴力破解

def find_plate_number():for i in range(1, 10):  # 首位1-9for j in range(10):  # 后位0-9if i != j:  # 前后数字不同plate = 1000*i + 100*i + 10*j + jfor temp in range(31, 100):  # 31²=961, 99²=9801if temp * temp == plate:return platereturn Noneprint(f"车牌号为：{find_plate_number()}")

算法流程图（Mermaid） 

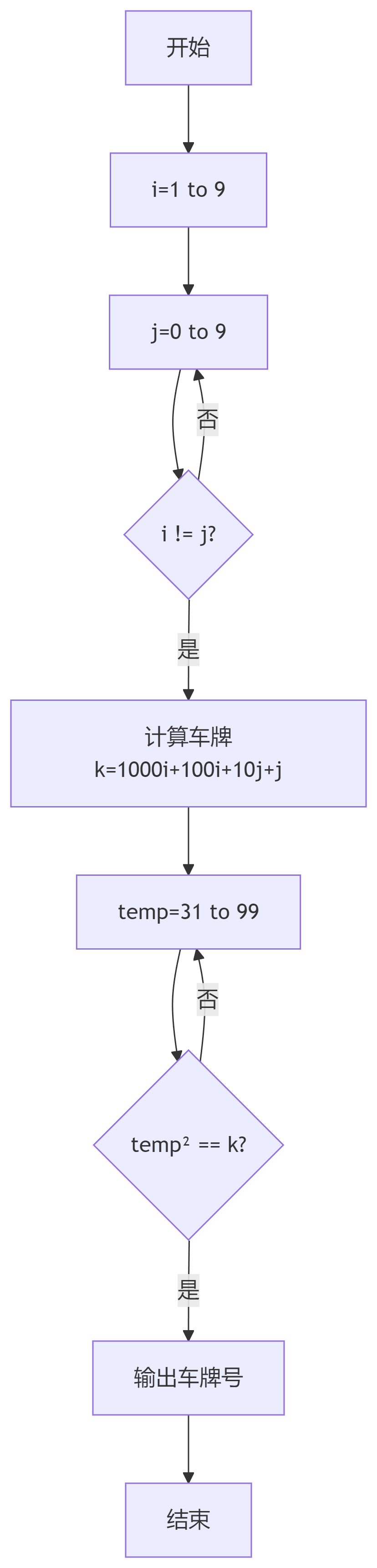
性能优化：减少无效循环

基础解法需执行9×10×69=6210次循环，可通过标志变量提前终止

def optimized_find():found = Falsefor i in range(1, 10):if found: breakfor j in range(10):if found: breakif i != j:k = 1100*i + 11*j  # 数学优化：1000i+100i+10j+j=1100i+11j# 平方根验证代替循环root = k ** 0.5if 31 <= root <= 99 and root.is_integer():print(f"车牌号为：{k}")found = Truebreak

数学优化：平方根验证法

关键突破：直接计算平方根验证整数性，消除最内层循环

import mathdef math_optimized():for i in range(1, 10):for j in range(10):if i == j: continuenum = 1100*i + 11*jroot = math.isqrt(num)if root * root == num:  # 精确整数平方验证return numreturn None

性能对比分析

方法	循环次数	时间复杂度	优化点
基础三重循环	≈6,210	O(n³)	无
标志变量优化	≈100	O(n²)	提前终止循环
平方根验证法	90	O(n²)	消除最内层循环

💡 优化效果：从6210次降到最多90次计算，性能提升近70倍！

完整代码实现 

#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author: 坐路边等朋友
# @desc: 交通肇事车牌智能识别import mathdef find_plate():"""数学优化版车牌查找函数"""for first in range(1, 10):    # 首位1-9for last in range(10):    # 末位0-9if first == last:     # 前后数字需不同continueplate = 1100 * first + 11 * lastroot = math.isqrt(plate)# 验证是否为完全平方数if root * root == plate:return platereturn "未找到符合条件车牌"if __name__ == "__main__":result = find_plate()print(f"交通肇事车牌号是：{result}")

运行结果验证

交通肇事车牌号是：7744

数学验证：

• 77相同，44相同，7≠4

• 7744 = 88² (88×88=7744)

算法拓展思考

1. 多解可能性：当前问题是否有唯一解？如何验证？

2. 扩展场景：若目击者记错一位数字，如何模糊搜索？

3. 性能极限：能否用O(1)时间复杂度解决？（提示：数学推导）

🚀 挑战题：如何修改算法，使其能处理5位或6位车牌号的情况？

总结与讨论

通过本案例我们展示了：

1. 问题建模：将现实问题转化为数学模型

2. 暴力解法：三重循环实现基础方案

3. 优化路径：标志变量→数学优化→平方根验证

4. 复杂度分析：从O(n³)到O(n²)的性能飞跃

讨论话题：你在解决类似问题时用过哪些优化技巧？欢迎在评论区分享你的优化案例！

更新于2025-07-18：增加复杂度分析表格，补充数学验证部分

版权声明：本文代码原创部分由CSDN博主「坐路边等朋友」提供，技术解析部分原创，转载请注明出处。